Distributed dynamic pricing based on demand-supply balance and voltage phase difference in power grid

Yoshihiro OKAWA,Toru NAMERIKAWA

Graduate School of Science and Technology,Keio University,3-14-1 Hiyoshi,Kohoku-ku,Yokohama,Kanagawa 223-8522,Japan

Received 5 October 2014;revised 10 March 2015;accepted 11 March 2015

Distributed dynamic pricing based on demand-supply balance and voltage phase difference in power grid

Yoshihiro OKAWA†,Toru NAMERIKAWA

Graduate School of Science and Technology,Keio University,3-14-1 Hiyoshi,Kohoku-ku,Yokohama,Kanagawa 223-8522,Japan

Received 5 October 2014;revised 10 March 2015;accepted 11 March 2015

This paper discusses a distributed decision procedure for determining the electricity price for a real-time electricity market in an energy management system.The price decision algorithm proposed in this paper derives the optimal electricity price while considering the constraints of a linearized AC power grid model.The algorithm is based on the power demand-supply balance and voltage phase differences in a power grid.In order to determine the optimal price that maximizes the social welfare distributively and to improve the convergence speed of the algorithm,the proposed algorithm updates the price through the alternating decision making of market participants.In this paper,we show the convergence of the price derived from our proposed algorithm.Furthermore,numerical simulation results show that the proposed dynamic pricing methodology is effective and that there is an improvement in the convergence speed,as compared with the conventional method.

Smart gird,real-time pricing,AC model of power grid

DOI 10.1007/s11768-015-4131-5

1 Introduction

Various studies have been conducted on how to develop future power networks,“smart grid”[1].Among these,severalstudies have suggested thatreal-time pricing of electricity can be a useful method for solving energy problems.We know that in general,the price of goods is determined by demand and supply.In this paper,based on the electricity liberalization,we discuss a process whereby the price of electricity price is determined by the demand and supply of power in a smart grid.In doing so,because a power network has many physical constraints,in addition to the economic problems associated with power distribution,these physical constraints must also be considered when developing the decision procedure for determining the electricity price[2].In particular,the power demand-supply balance should be such that it ensure stable operation ofthe power distribution system.A further complication is that with the increase and development of renewable energy technologies,both power consumers and suppliers are distributed over multiple areas in a smart grid.Therefore,the optimal electricity price in a smart grid must be determined according to the area to satisfy the power balance of a whole power network.

The decision problem ofdetermining the optimalelectricity price by area or node has been studied as optimal power flow(OPF)or locational marginal price(LMP)from quite some time[3–5].However,most of these studies are on determining the optimal price based on the minimization of the cost of power generators and do not consider cost benefits for consumers.There are some literature on market mechanism to determine the electricity price in which both the powersupplierand the powerconsumerare considered.In[6,7],the behavioral model of consumers is represented by a utility function and a distributed algorithm was proposed to derive the optimal electricity price.Furthermore,the paper[8]did considerthe issue ofpowerflow and defined the optimal problem with the constraints of the power flow under Kirchhoff’s current and voltage laws;also,the paper[9]considered the same but with DC approximation.Including the above ones,various decision algorithms for determining optimal electricity price have been studied actively.However,the convergence speed of these algorithms has not been a focus till now.For this problem,the paper[10]applied the iterative gradientmethod with line search to the price decision algorithm.Though this method can improve its convergence speed compared with the original gradient method,it requires the information of the private functions of power supplies and consumers.

In this paper,we propose a distributed decision procedure for determining electricity price based on the power demand-supply balance and the voltage phase differences,which are decided alternately by each market participant.The goal of this price decision method is to derive the optimal locational electricity prices which maximize the social welfare of power networks under the physical constraints of power grids.The social welfare considered in this paper includes economic profits for power consumers as well as those for power suppliers.In order to derive these optimal prices distributively and to improve its convergence speed without any private functions of market participants,we propose a price decision algorithm based on an alternating decision making of market participants.Specifically,in our proposed algorithm,locational electricity prices are updated with the information of power demand,supply and voltage phase angles which are alternately determined by each market participant until the power balance of a whole power network is satisfied.Thus,the proposed algorithm can derive the optimal locational prices which maximize the social welfare without any private functions of market participants under the constraints of a power grid.

The rest of the paper is organized as follows:First,the behavior model of each market participant and the constraint conditions of a linearized AC power grid are given in Section 2.Next,in Section 3,we define social welfare as the objective function and the optimal price that maximizes the social welfare.In Section 4,we propose a novel market algorithm that derives the optimal price distributively and shows the convergence property of the price.Finally,in Section 5,through numerical simulation results,we show the feasibility of our proposed algorithm and the improvement in the convergence speed.

2 Problem definition

Fig.1 shows the model of the electricity market considered in this paper.We consider three types of participants in the market model:power consumers,power suppliers,and an independent system operator(ISO).Here,the ISO is a nonprofit organization responsible for operating the electricity market and organizing power transmission.It is proposed that the decision procedure for determining the optimal electricity price is based on the information exchange among these market participants.

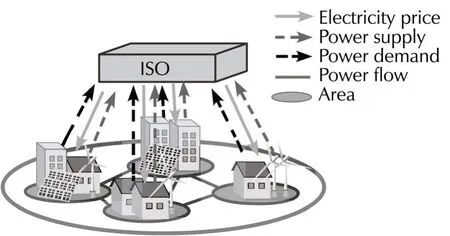
Fig.1 Electricity market and its information flow.

2.1 Decision procedure of the optimal electricity price

The following five steps show the decision procedure ofthe optimalelectricity by the hour.Here,the ISOisassumed to be able to transmit the price to all consumers and suppliers.

1)The ISO determines the initial electricity price per unit,which varies according to the area,and transmits this information to all consumers and suppliers.

2)According to the price information,each consumer and supplier decides its own power demand and supply,respectively.Then,each consumer and supplier reports this information to the ISO.

3)The ISO decides the voltage phase differences among areas based on the demand and supply reported from each consumer and supplier.

4)If the demand,supply,and voltage phase differences decided by each market participant satisfies the constraints of the power grid,the ISO determines the current price as the optimal price.If they do not satisfy the constraints,the ISO updates the electricity price per unit and transmits the updated price to consumers and suppliers.

5)Back to 2)and repeat 2)to 4)until the constraints of the power grid are satisfied.

In this way,because the ISO decides the electricity price based on the information reported from other market participants,the proposed method allows deriving the optimal price distributively,which maximizes the social welfare in a smart grid.

2.2 Models of consumer and supplier behavior

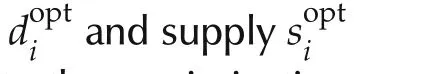
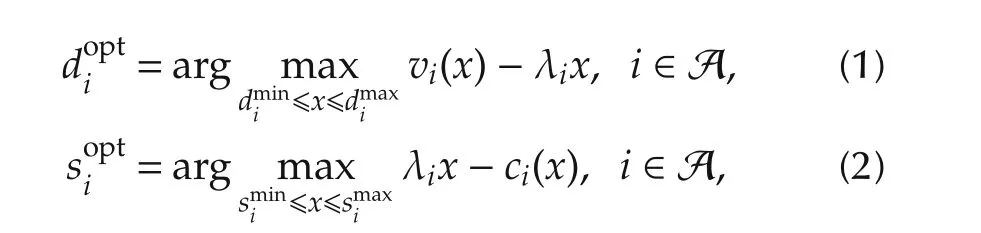
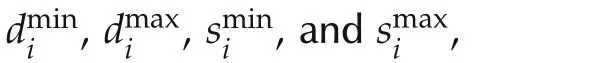
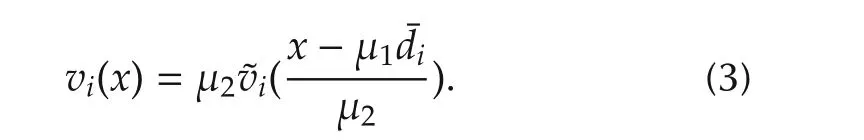
Here,the following assumptions are introduced for the utility functionvi(x)and the cost functionci(x),respectively.

Assumption 1Each utility functionvi(·)is inC2(0;∞),strictly increasing and strictly concave for alli∈A.

Assumption2Each cost functionci(·)is inC2[0;∞),strictly increasing and strictly convex for alli∈A.

First,Assumption 1 means that while the utility functionvi(x)increases according to the increase of power consumption,the satisfaction saturates if the consumption becomes large enough,as shown in Fig.2.Meanwhile,the suppliers in each area are assumed to start their generators,which have low cost one after another,and then the cost functions are strictly convex functions with Assumption 2,as shown in Fig.3.

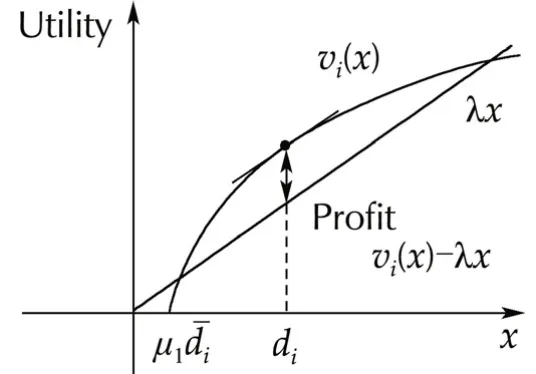
Fig.2 Utility function.

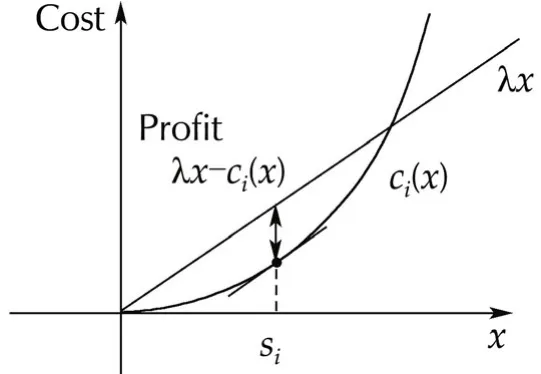
Fig.3 Cost function.

2.3 Power grid model using AC generators

In this paper,suppose that there are n nodes in the power grid as well as area numbers.In addition,the following assumptions are introduced for the power grid model:

Assumption 3The power grid is assumed to satisfy the following properties:

1)Resistance loss in the transmission grid is negligible.

2)The voltage of each node approximately equals to 1(p.u.).

3)The voltage phase difference between each node is sufficiently small.

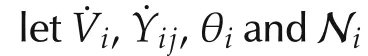
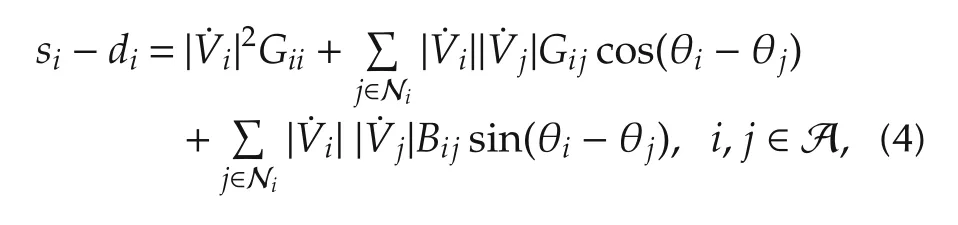
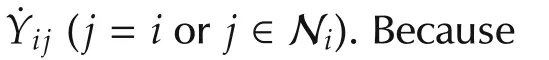
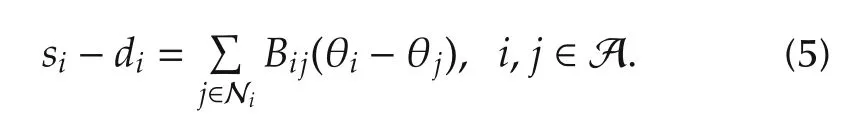
Then,the active power flow equation of a whole power network is given by

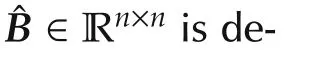
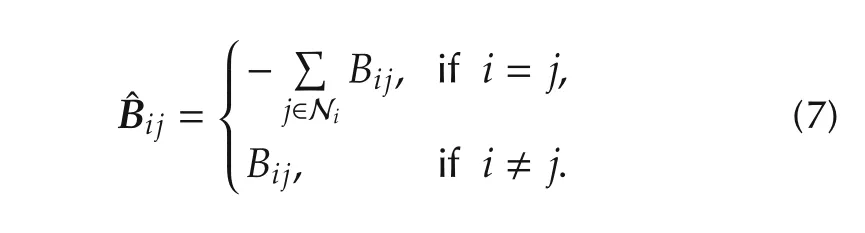
Next,the reactive power is considered.With Assumption 3,the following equation for reactive power is obtained:

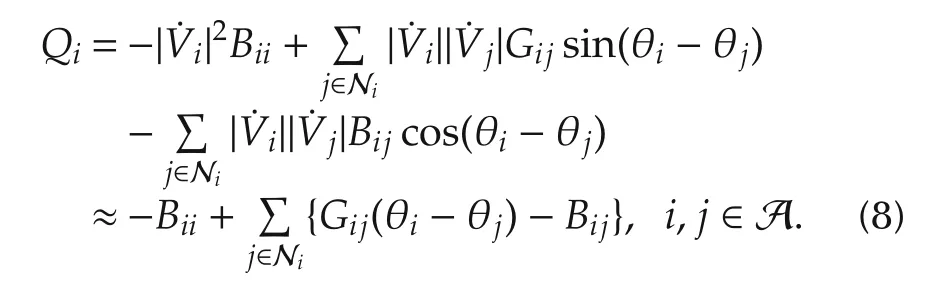
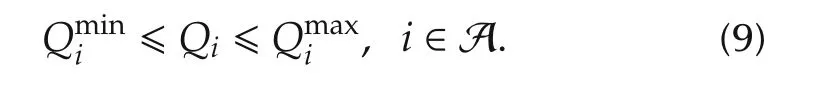
Finally,the line capacity of each line connecting areas is considered.The active power Pijwhich flows node i to node j(i,j∈Ni)is defined as follows:

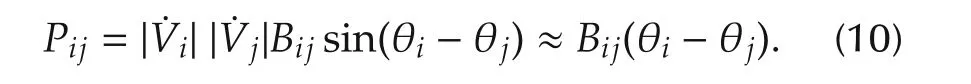
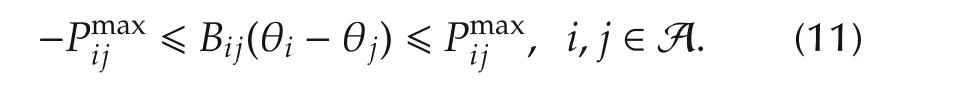
The following assumption is introduced for the upper and lower bounds of the power supply,the power demand and the voltage phase difference in each area.

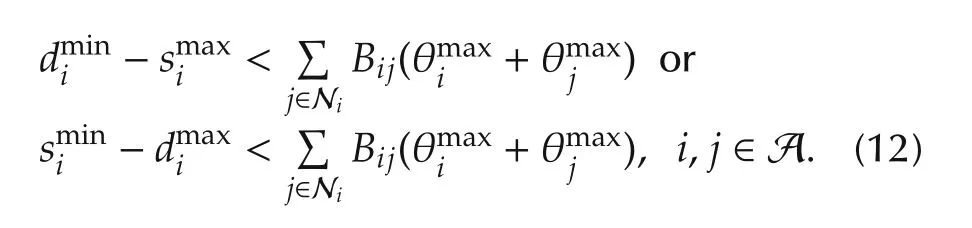
This assumption means that the gap between the power demand and its supply in every area is lower than the maximum power flow from the other neighbor areas.Furthermore,this assumption is required to guarantee the existence of a solution to the optimization problem described in the next section.

3 Maximization of social welfare

3.1 Social welfare

In this paper,the social welfare Wallis defined as the difference between the sum of the profits of the whole consumers and generators represented by(1)and(2)and the change cost of the voltage phase difference,and it is given by

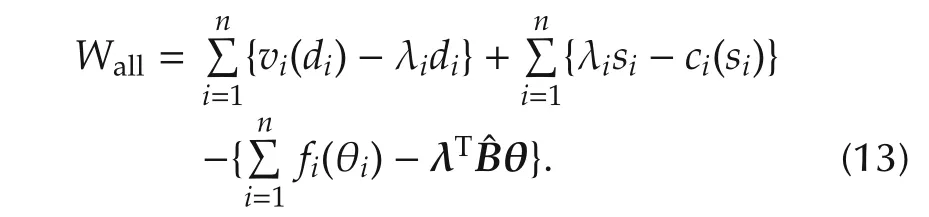
In the above equation,λ =[λ1λ2···λn]Tis the vector of the price of each area,andfi(θi)is the cost function of the voltage phase differences,which represents the economic cost to change or adjust the voltage phase angle of each node.Here,the following assumption is introduced in this cost function.

Assumption5Cost functionsfi(θi) are in C2(−π,π),and strictly convex for alli∈ A.

Assumption 5 represents that a large amount of economic cost is required to change or adjust the voltage phase angle as the angle difference between each node and the slack node increases.Furthermore,this assumption also represents that the physical loss caused by approximate errors increases if angle differences increase,since active power flows are calculated by using the DC approximation as described in the previous section.

In addition,the last term in the right hand side of(13),λTˆBθ,represents an economic profit generated by power flow and price differences among areas.Thus,the social welfare in(13)means an economic profit of a whole power network considering power flows among areas.

Then,rewriting(13)with λ,s=[s1···sn]Tandd=[d1···dn]T,the social welfareWallbecomes as

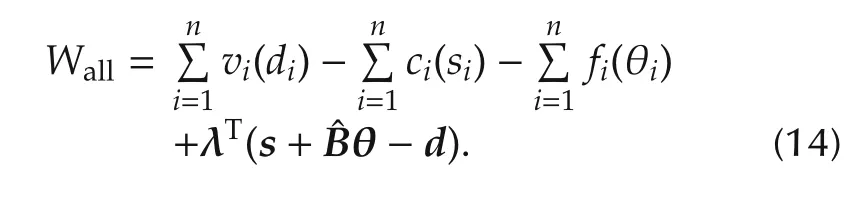
Here,s+ˆBθ−d=0holds because of the constraint of active power in(6).Therefore,the problem is equal to seeking the optimal power supply,demand,and voltage phase difference,which maximizes social welfareWall,and this problem is given as the following optimal problem(15)–(21).

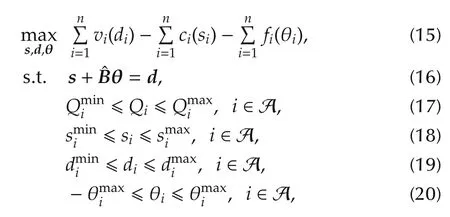
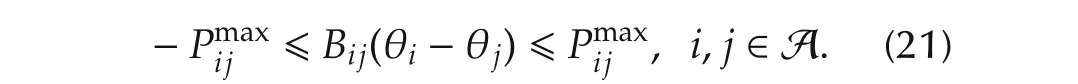
In the above optimal problem,the constraint conditions(16)–(21)represent the active power flow equation,and the upper and lower bound of the reactive power,the power demand,the power supply,the voltage phase difference,and the line capacity,respectively.Here,from Assumption 4,since there isthe solution to the combination ofthe powersupply,demand,and voltage phase difference,(s,d,θ),which satisfies the equality constraint(16)and strictly satisfies the inequality constraints(17)–(21),the optimal problem(15)–(21)satisfies the Slater’s condition.

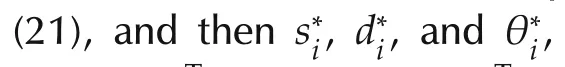
3.2 Optimal electricity price

In this section,it is shown that the optimal electricity price can be represented with the optimal solution to Lagrange dual function of the optimal problem(15)–(21).In addition,it is also shown that the optimal electricity prices lead consumers and suppliers to consume and supply the optimal power demand and supply,respectively.

First,let us define the Lagrange function of problem(15)–(21)by

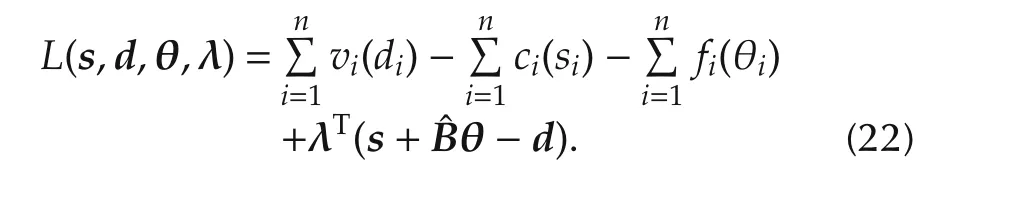
We also define the sets of the power demand,power supply,and the voltage phase difference,which satisfy the constraints condition in(16)–(21)as follows:

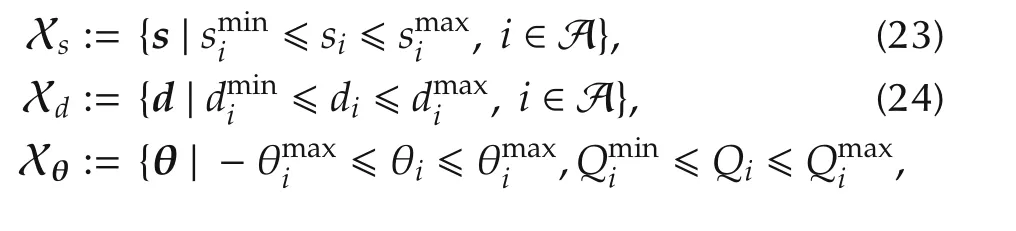
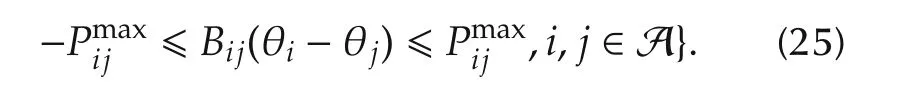
Then,the dual problem of(15)–(21)is given as follows:

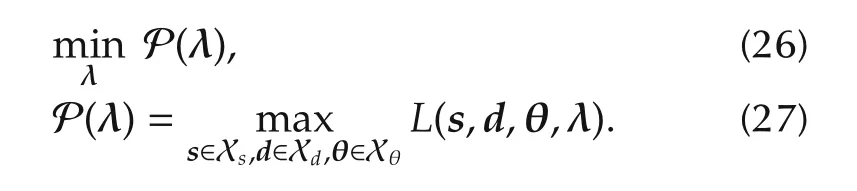
For this dual problem,the following lemma is obtained with the optimal solution to(26),λ∗.

Lemma 1Suppose that Assumptions 1-5 hold.The solutions(s∗,d∗,θ∗,λ∗)is the saddle point of the Lagrange functionL(s,d,θ,λ).

ProofThe proof is clear from the saddle point theorem. □

Based on Lemma 1,the following theorem is obtained.

Theorem 1Suppose that Assumptions 1–5 hold.In addition, λ∗iwhich is theith component of λ∗=[λ∗1···λ∗n]Tis defined as the electricity price of Areai.Then,the power demand or power supply of Areaiaccording to(1)and(2)agree with the optimal solution to the problem(15),d∗iands∗i,respectively.

ProofFrom Lemma 1,the following equation holds:

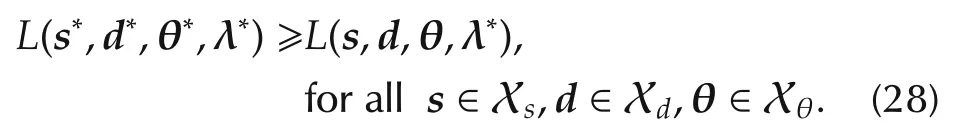
Hence,(s∗,d∗,θ∗)is the solution to the following optimal problem:

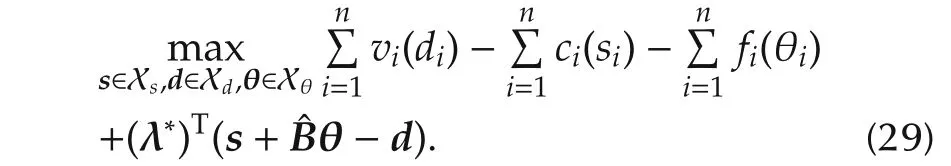
Here,since(29)is independent fors,dand θ,respectively,this equation can be divided as follows:

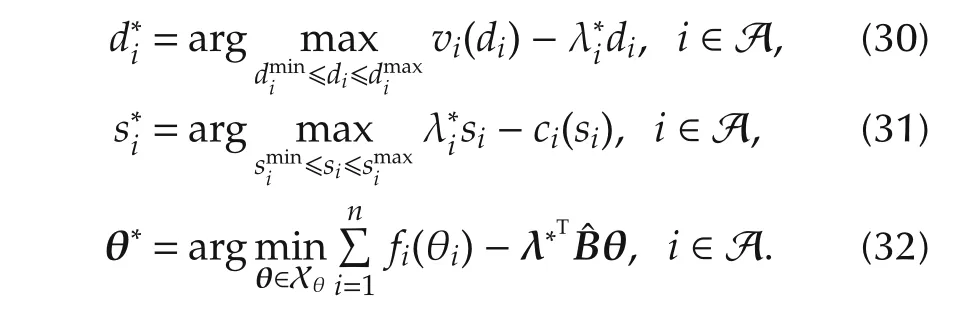
From the above equations,(30)and(31)agree with the selfish behavior models of the consumers and suppliers represented by(1)and(2).Therefore,with the electricity price oftheith areaλ∗i,the powerdemand and supply of each area agree with the optimal solutionsd∗iands∗i,respectively. □

4 Distributed optimal market algorithm

In the previous section,it is shown that the optimal electricity price can be obtained with the optimal solution to the dual function.Here,as also mentioned in the previous sections,the ISO can not derive an optimal solution to the dual function directly since the ISO does not know the functions of the other market participants.For this problem,the distributed algorithm based on a gradient method has been proposed in[6].In this distributed algorithm,the optimal price is obtained by exchanging information among market participants.However,since each market participant makes its own decision independently,this algorithm requires a large number of updating until the prices converge to the optimal ones.Meanwhile,recently,the alternating direction method of multipliers(ADMM)has been studied as a distributed algorithm for optimal problems[12],and ADMM algorithms for the OPF problem to minimize the costs of generators are proposed in[13,14].Then,in this paper,we propose the ADMM algorithm to maximize social welfare which includes the benefits for power consumers described in the previous section.However,when this ADMM is applied to the optimal problem considered in this paper,the determination of the power demand and supply in a certain area requires information of power demand and supply of otherareas.However,in ourproposed distributed marketalgorithm,the consumersand suppliersdetermine theirown power demand and supply independently and report them to the ISO,and then the ISO determines the voltage phase differences according to the reported power demand and supply.In this way,the consumers and suppliers and the ISO determine their own values alternately,the proposed method improves its convergence speed and also derives the optimal price distributively.

The proposed algorithm is as follows.

Algorithm 1

Step 1(Decision ofthe initialprice) The ISOdecides the initial electricity price of every area λ0=[λ01···λ0n]arbitrarily,and transmits each price to each consumer and supplier.

Step 2(Decision of the power demand and supply)Based on the electricity price λkifrom the ISO,consumers and suppliers in each area decide their own power demand and supply according to the following equations,and report them to the ISO.

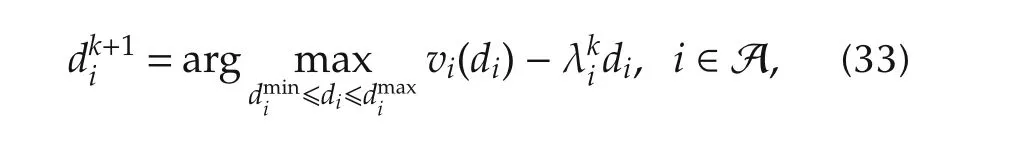
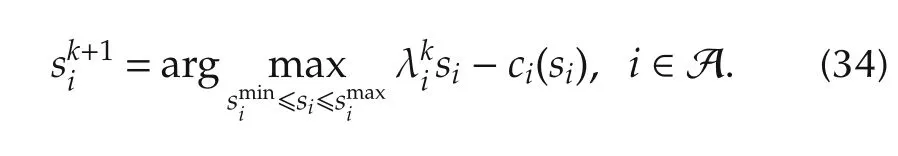
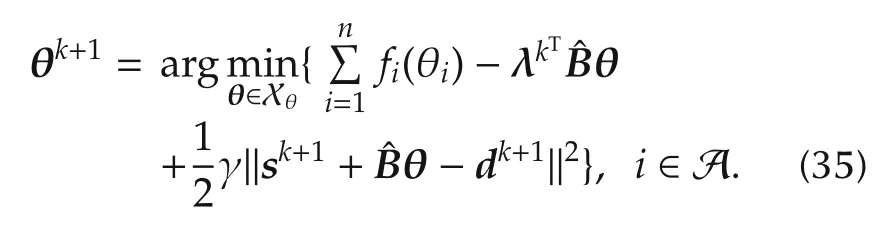
Step 4(Decision or update of the electricity price) If the powerdemand and supply reported from consumers and suppliers and the voltage phase difference decided by the ISO satisfy the following active power flow equation,the ISO determines λkias the actual electricity price in Areai(i∈A).

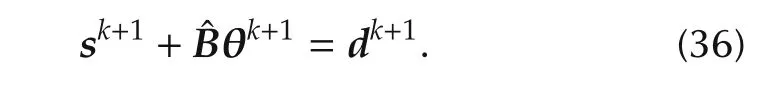
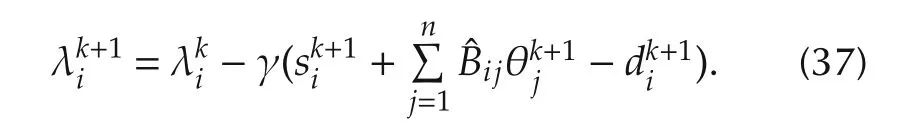
Step 5(Repetition) Change the iteration numberktok+1 and back to Step 2.

In the above algorithm,the ISO updates the electricity price according to(37)with the power demand and supply reported by consumers and suppliers.This means that the ISO does not need the information of market participants such as utility functions or cost functions.Therefore,by using this proposed algorithm,the optimal prices can be obtained in a distributed manner through the exchange of information of each market participant.

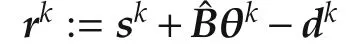
Theorem 2Suppose that Assumptions 1–5 hold.If the step size γ satisfies the following inequality,the electricity price λkupdated by the proposed algorithm converges to the optimal one λ∗.

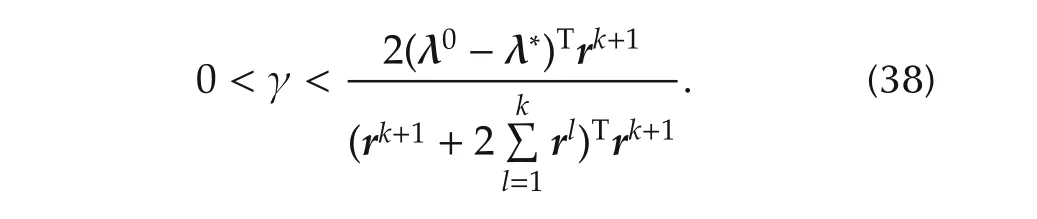
ProofFirst,let us define the Lyapunov functionV(λk)as follows:

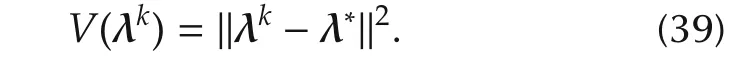
Here,the updating equation of the prices in all area is given by

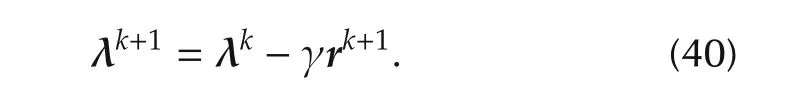
By using this equation,V(λk+1)becomes as follows:

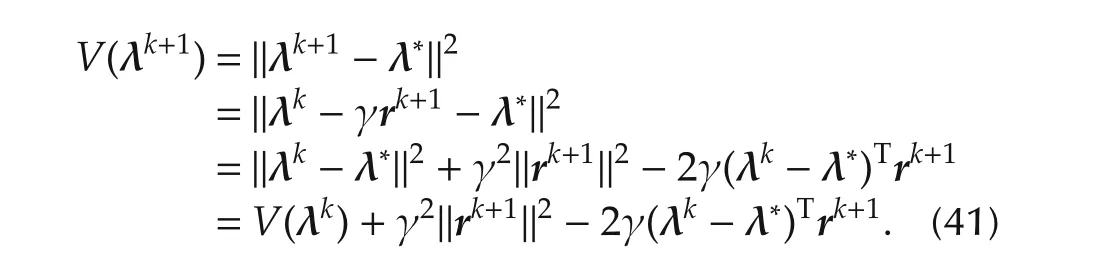
Then,the difference of the Lyapunov function ΔV:=V(λk+1)−V(λk)becomes as

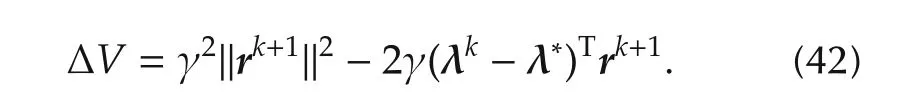
Here,from(22),(26)and(27),rk+1=sk+1+ˆBθk+1−dk+1is equal to the gradient of the dual function P(λk).Then,since P(λk)isa convex function because ofAssumptions 1–3,the following inequality holds:

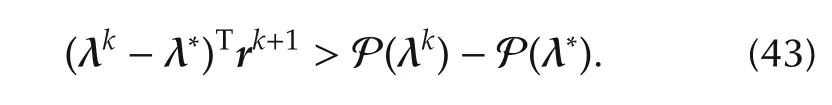
Furthermore,from(26)and(27),since the optimal price λ∗minimizes the dual function P(λ),the right side of the above inequality,P(λk)− P(λ∗),is positive for allk.As a result,(λk− λ∗)Trk+1is also positive for allk.

Meanwhile,the price λkin stepk(≥ 1)is represented with the initial price λ0as follows:

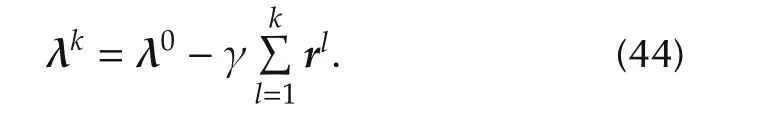
Substituting the above equation in(42),ΔVbecomes as follows:

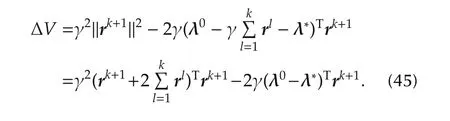
Therefore,the difference ΔVbecomes negative(ΔV＜ 0)if the step size γ (＞ 0)satisfies the following condition in each step.

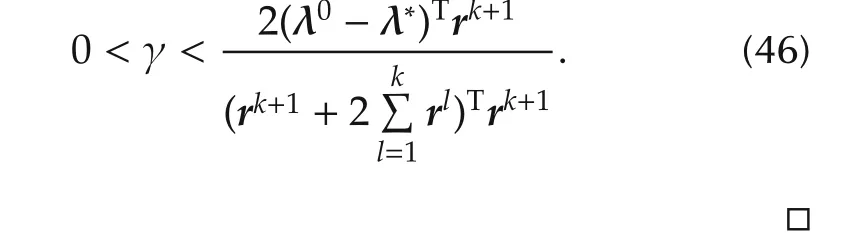
From Theorem 2,it is shown that the electricity price converges to the optimal one with the exchange of information among the ISO and the other market participants.

5 Simulation verification

In this section,we verify the feasibility ofthe proposed price decision algorithm through numerical simulation.

5.1 Simulation conditions

The power grid model used in this simulation is depicted in Fig.4,which is a part of the IEEE 14 bus system.Also,the data of the actual load in each bus,¯diand the parameters of the blanches connecting each bus are given in[15].

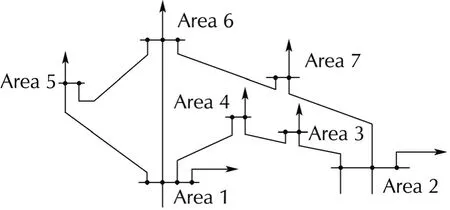
Fig.4 Power grid model.

Meanwhile,vi(di),ci(si),andfi(θi),which are the utility function of consumers in Areai,the cost function of suppliers in Areai,and the cost function of the voltage phase difference in Areai,respectively,are defined as follows so that they satisfy Assumptions 1,2 and 5.

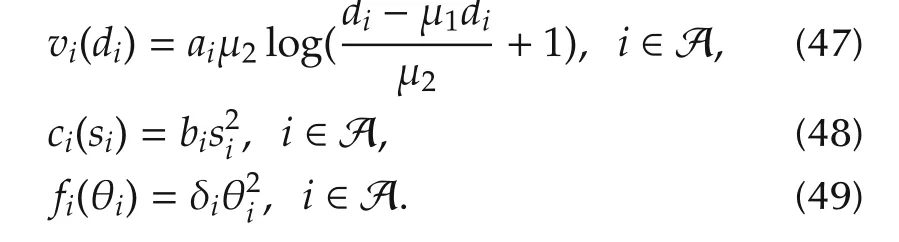
In(47), is the inelastic power demand for price.

The process of the decision method of each parameter is as follows.First,μ1and μ2are decided considering the elasticity of the power demand for price.Next,coefficients of the utility function and cost function,aiandbi,are decided by the following equations with the fixed electricity price λf:

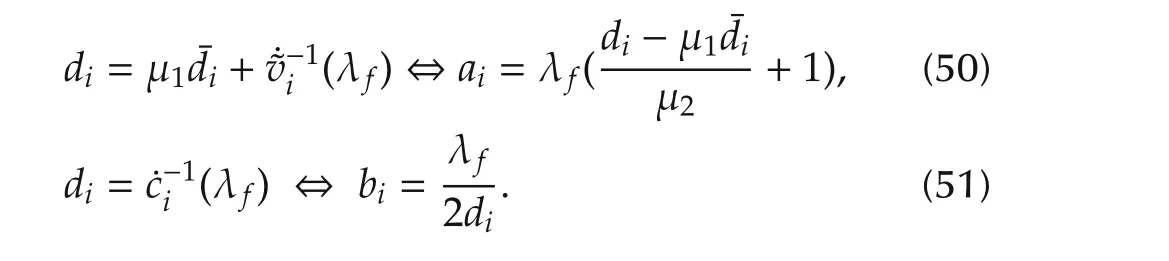
By using the parameters;aiandbidetermined in the above equations,we can simulate that power consumer or supplier in each area has a different scale of a utility or cost function which depends on the amount of the power demand in its own area.In this simulation,μ1=0.67,μ2=0.2,δi=1.0×105,i∈ A,and the other parameters are shown in Table 1.

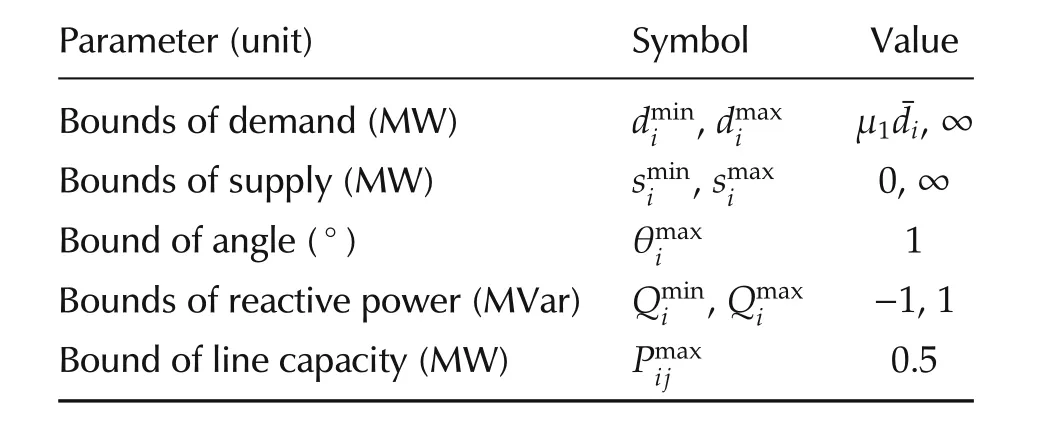
Table 1 Simulation parameters.

5.2 Simulation results

5.2.1 Case 1:Feasibility of the proposed algorithm

Figs.5 and 6 show the price and the power balance in Area 2 between 13:00–14:00(h),respectively.In this and the following figures,“Step”on the horizontal axis represents the number of iterations in the price decision algorithm.The dotted line and dashed line represent the results obtained using the conventional method based on a gradient method with constant step sizes,γ=3.0×102and 4.0×102,respectively.The solid line represents the result obtained using our proposed method with a constant step size γ =1.2×103which satisfies Theorem 2.

From Fig.5,it can be confirmed that the electricity price with the proposed algorithm converges to the optimal price λ∗2=28.78 Yen/kWh,which is obtained by solving the optimization problem in(26)and(27)directly.In addition,though fluctuation is occurred in the conventional method with a big step size γ=4.0×102,our proposed method can achieve to improve the convergence speed without fluctuation.Also,in Fig.6,it is confirmed that the power balance in Area 2 becomes 0 according to the convergence of the price in Area 2 as shown in Fig.5.Furthermore,the convergence speed is improved without fluctuation by using our proposed method.

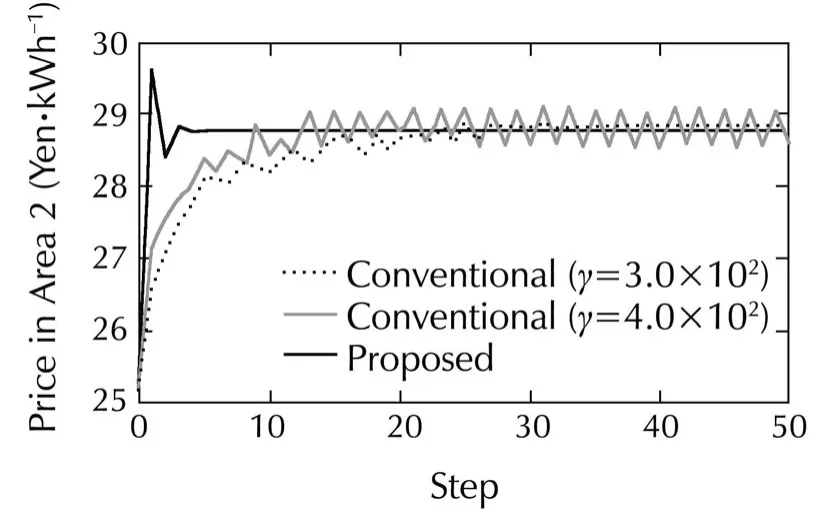
Fig.5 Electricity price in Area 2.

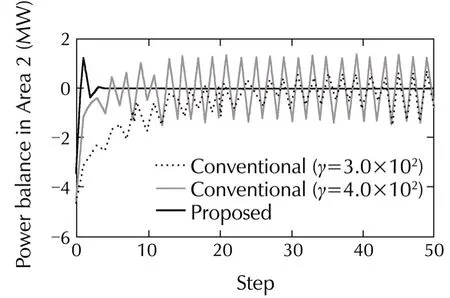
Fig.6 Power balance in Area 2.

5.2.2 Case 2:Response to the change of physical constraints

Fig.7 shows the response results of the prices to this change of constraint of a physical system.In this figure,the prices in Area 3 and in Area 2 and 4,which are directly connected to Area 3,and the price in Area 7,which are notdirectly connected to Area 3,are shown.In addition,similar to figures in the previous subsection,the dotted lines represent the results obtained using the conventional method with γ =3.0× 102,and solid lines represent the results obtained with the proposed method γ=1.2×103.

From this figure,the price in each area starts to change after accidents occur in step 50.Then by updating the prices repeatedly with the proposed market algorithm,these prices converge again without fluctuation unlike the results via the conventional gradient method.

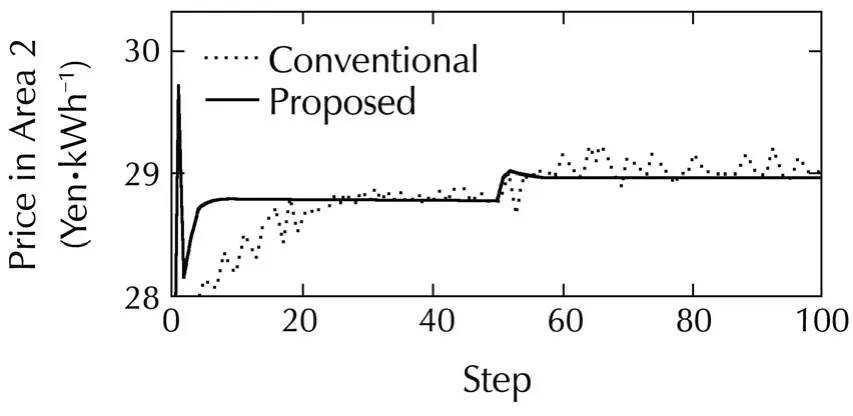
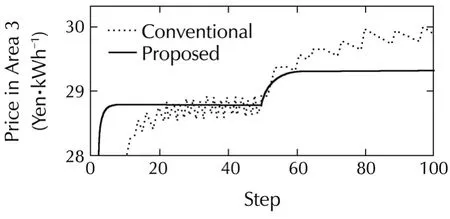
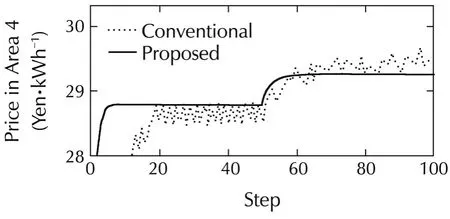
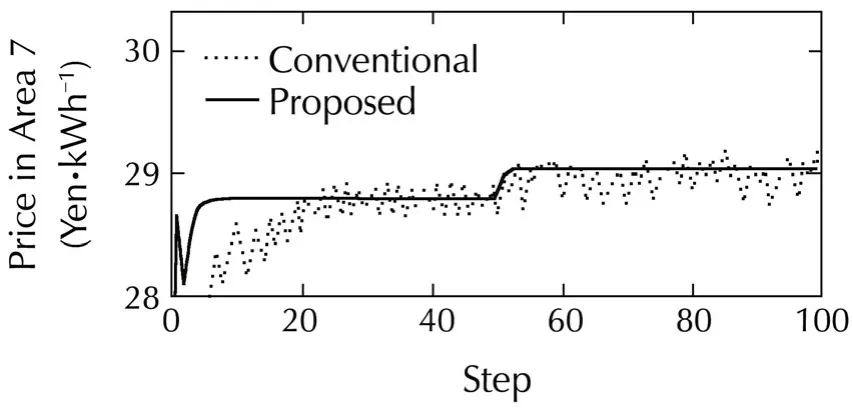
Fig.7 Electricity Price in Areas 2–4 and 7.

Fig.8 shows active power flows among areas in Case 2.In this figure,Line numberi-jrepresents the active power flow from Areaito Areaj,and if the values is negative,it means that the active power flows from Areajto Areai.From this figure,by changing the prices,as shown in Fig.7,power flow occurs among areas.In particular,the transmission powers to Area 3 from Areas 2 and 4 become larger under the constraint of the line capacity.This means that the shortage of the power supply in Area 3 caused by the accident in generators is compensated by the power flow from other connecting areas with our proposed price decision algorithm.At the same time,it can be confirmed in Fig.7 that the price in Area 3 becomes higher than the prices in the other areas.This is because the power demand in Area 3 has to be reduced,since the transmission power between Areas 2 and 3 reaches its maximum value,Pmax23=0.5 MW as shown in Fig.8.From these results,we can conclude that our proposed algorithm can derive the optimal locational electricity prices by responding to the change in a physical system.

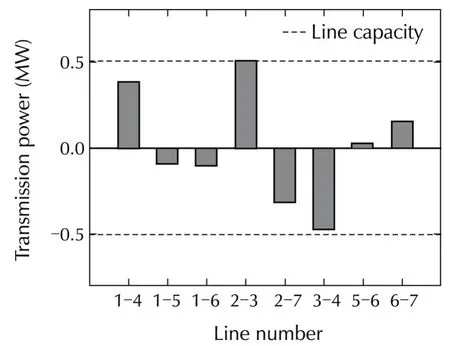
Fig.8 Transmission power.

6 Conclusions

This paper discusses a model of a real-time electricity market in an energy management system;we propose a distributed decision procedure to determine the electricity price based on the power balance including power flow among areas.In the proposed algorithm,the locational electricity prices are updated with the information of the power demand,supply and voltage phase angles which are alternately determined by power consumers and suppliers in each area and the ISO.As a result,our proposed algorithm achieves to derive the optimal locational prices distributively and to improve its convergence speed without any private functions of market participants.In this paper,we show that the optimal locational prices maximize the social welfare of power networks which includes profits of both power consumers and suppliers under the physical constraints ofpowergrids.Also,we prove the convergence property of the proposed price decision algorithm.Simulation results confirm the feasibility of our proposed algorithm and the improved convergence speed compared with a conventional gradient method;they also confirm that our proposed algorithm can derive the optimal price of each area by responding to the change in a physical system.

[1]T.Namerikawa,T.Kato.Distributed load frequency control of electrical power networks via iterative gradient method.Proceedings of the IEEE Conference on Decision and Control and European Control Conference,Orlando,FL:IEEE,2011:7723–7728.

[2] E.Bitar,P.P.Khargonekar,K.Poolla.System and control opportunities in the integration of renewable energy into the smart grid.Proceedings of the 18th IFAC World Congress,Milano:IFAC,2011:4927–4932.

[3]A.J.Conejo,J.A.Aguado.Multi-area coordinated decentralized DC optimal power flow.IEEE Transactions on Power Systems,1998,13(4):1272–1278.

[4] A.Jokic,M.Lazar,P.P.J.van den Bosch.Real-time control of power systems using nodal prices.International Journal of Electrical Power and Energy Systems,2009,31(9):522–530.

[5]J.Warrington,P.Goulart,S.Mari´ethoz,etal.Amarketmechanism for solving multi-period optimal power flow exactly on AC networks with mixed participants.Proceedings of the American Control Conference,Montreal:IEEE,2012:3101–3107.

[6]P.Samadi,A.Mohsenian-Rad,R.Schober,et al.Optimal realtime pricing algorithm based on utility maximization for smart grid.Proceedings of the IEEE International Conference on Smart Grid Communications,Gaithersburg:IEEE,2010:415–420.

[7]N.Ito,A.Takeda,T.Namerikawa.Convex Hull pricing for demand response in electricity markets.Proceedings of the IEEE International Conference on Smart Grid Communications,Vancouver:IEEE,2013:151–156.

[8]M.Roozbehani,M.Dahleh,S.Mitter.Dynamic pricing and stabilization of supply and demand in modern electric power grids.Proceedings of the IEEE International Conference on Smart Grid Communications,Gaithersburg:IEEE,2010:543–548.

[9]G.C.Chasparis,A.Rantzer,K.J¨ornsten.A decomposition approach to multi-region optimal power flow in electricity networks.Proceedings of the European Control Conference,Zurich:IEEE,2013:3018–3024.

[10]Y.Okawa,T.Namerikawa.Dynamic pricing considering constraints of power grids.Proceedings of the SICE Annual Conference,Sapporo:IEEE,2014:1484–1489.

[11]P.Kundur.Power System Stability and Control.New York:McGraw-Hill,1994:255–269.

[12]S.Boyd,N.Parikh,E.Chu,et al.Distributed optimization and statistical learning via the alternating direction method of multipliers.Foundations and Trends in Machine Learning,2010,3(1):1–122.

[13]E.D.Anese,H.Zhu,G.B.Giannakis.Distributed optimal power flow for smart microgrids.IEEE Transactions on Smart Grid,2013,4(3):1464–1475.

[14]T.Erseghe.Distributed optimal power flow using ADMM.IEEE Transactions on Power Systems,2014,29(5):2370–2380.

[15]Power Systems Test Case Archive.Seattle:University of Washington,1999:http://www.ee.washington.edu/research/pstca/.

his B.E.and M.E.degrees from Keio University,Japan,in 2012 and 2013,respectively.He is currently pursuing his Ph.D.at Keio University.His research interests include robust control,control systems,and real-time pricing in power network systems.E-mail:yoshihiroo@nl.sd.keio.ac.jp. — ——–

Toru NAMERIKAWAreceived the B.E.,M.E.,and Ph.D.in Engineering in Electrical and Computer Engineering from Kanazawa University,Japan,in 1991,1993,and 1997,respectively.From 1994 until 2002,he was with Kanazawa University as an assistant professor.From 2002 until 2005,he was with the Nagaoka University of Technology as an associate professor.From 2006 until 2009,he was with Kanazawa University again.In April 2009,he joined Keio University,where he is currently a professor in the Department of System Design Engineering.His main research interests are robust control,nonlinear control,cooperative control theories,and their application to power network systems and robotic systems.He is a member of ISCIE and IEEE.E-mail:namerikawa@sd.keio.ac.jp.

†Corresponding author.

E-mail:yoshihiroo@nl.sd.keio.ac.jp.Tel.:+81 45-563-1151;fax:+81 45-566-1720.

This work was supported by the Core Research for Evolutional Science and Technology,Japan Science and Technology Agency(JST-CREST).

©2015 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg