New adaptive vector control methods for induction motors with simpler structure and better performance

Kang-Zhi LIU,Masashi YOKOO,Keiichiro KONDO,Tadanao ZANMA

Department of Electrical and Electronics Engineering,Chiba University,Chiba 263-8522,Japan

Received 30 October 2014;revised 12 March 2015;accepted 13 March 2015

New adaptive vector control methods for induction motors with simpler structure and better performance

Kang-Zhi LIU†,Masashi YOKOO,Keiichiro KONDO,Tadanao ZANMA

Department of Electrical and Electronics Engineering,Chiba University,Chiba 263-8522,Japan

Received 30 October 2014;revised 12 March 2015;accepted 13 March 2015

This paper deals with the vector control,including both the direct vector control(DVC)and the indirect vector control(IdVC),of induction motors.It is well known that the estimation of rotor flux plays a fundamental role in the DVC and the estimation of rotor resistance is vital in the slip compensation of the IdVC.In these estimations,the precision is significantly affected by the motor resistances.Therefore,online estimation of motor resistances is indispensable in practice.

For a fast estimation of motor resistances,it is necessary to slow down the convergence rate of the current estimate.On the other hand,for a fast estimation of the rotor flux,it is necessary to speed up its convergence rate.It is very difficult to realize such a trade-off in convergence rates in a full order observer.

In this paper,we propose to decouple the current observer from the flux observer so as to realize independent convergence rates.Then,the resistance estimation algorithm is applied to both DVC and IdVC.In particular,in the application to IdVC the flux observer needs not be used,which leads to a simpler structure.Meanwhile,independent convergence rates of current observer and flux observer yield an improved performance.A superior performance in the torque and flux responses in both cases is verified by numerous simulations.

Induction motor,current observer,flux observer,parameter adaptation,indirect vector control,direct vector control

DOI 10.1007/s11768-015-4153-z

1 Introduction

It is well-known that the vector control technology[1]has greatly contributed to the variable speed control and energy-saving of motor drives.There are mainly two kinds of vector control methods:direct vector control(DVC)and indirect vector control(IdVC)[1].Both methods are model-based and heavily depend on the motor parameters.The rotor resistance is needed both in the rotor flux estimation of DVC and in the slip frequencycomputation of IdVC.

However,the stator and rotor resistances of an induction motor vary significantly with the operating temperature.The resistance uncertainty leads to the deviation of rotor flux estimate in DVC and the error of slip frequency in IdVC,thus results in torque errorin the steady state.

1.1 Direct vector control

In the DVC,the rotor flux is used in the transformation between the d-q frame and γ-δ frame,thus plays a fundamental role[1].Since the rotor flux cannot be measured,conventionally it is estimated based on its model[1,2]in an open-loop manner.Furthermore,flux estimation with correction term was studied in[2,3].

It is well recognized that the precision of flux estimation depends heavily on the motor resistance(refer to equation(2)for the detail).The variation of rotor resistance causes a deviation of the frame,which results in errors in both flux and torque.In particular,reference[3]revealed that almost all types of open-loop flux observer(no matter full order or reduced order)are sensitive to the uncertainty of motor parameters.Even though this sensitivity may be alleviated to a certain degree with a current correction term added to the flux observer,parameter uncertainty still has a substantial influence on the precision of flux estimate.

1.2 Indirect vector control

The compensation of slip frequency is the core of the IdVC method,which controls the rotor flux(refer to Fig.1).The slip frequency

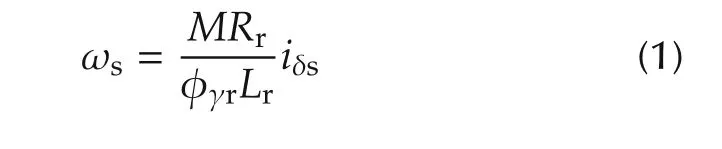
is proportional to the rotor resistance Rr.Therefore,its variation directly affects the precision of rotor flux,compensation of the frequency of electrical source as well as the associated phase angle used in frame transformation.

For the reasons stated above,it is difficult to achieve the desired control performance in vector controls withoutonline adaptation ofrotorparameters.Therefore,online estimation of resistance is indispensable in practice in order to achieve high performance.

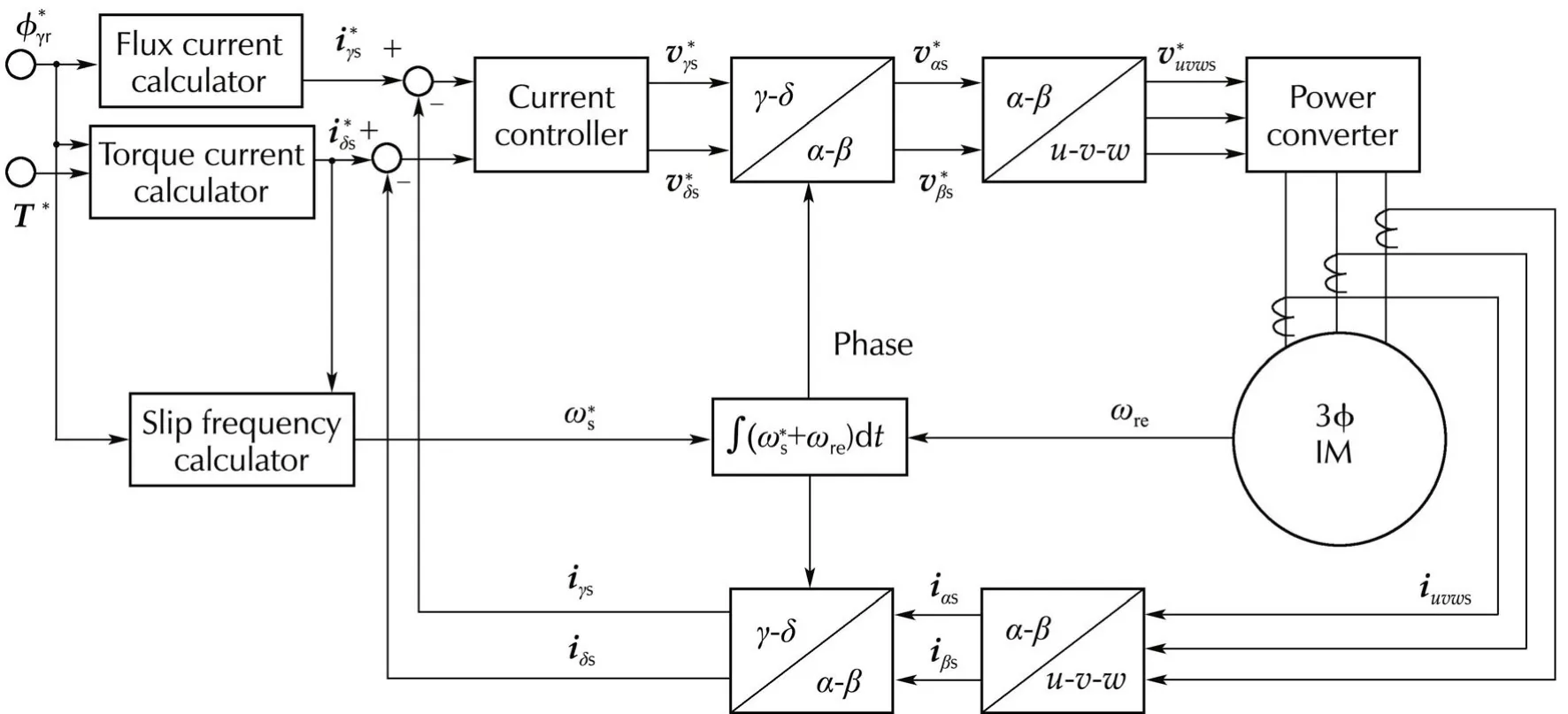
Fig.1 IdVC system.

1.3 Existing adaptive methods

As an approach to resolve such problem,one may add a parameter adaptation law to the control system.A rotorresistance identification method was proposed in[4],which is based on the model reference adaptive method and uses a rotor flux observer.However,a sinusoidal signal needs to be injected into the flux reference.Subject to the same condition of sinusoidal signal injection,reference[5]gave a method for the adaptation of stator and rotor resistances in the speed sensorless circumstance.Reference[6]proposed a parameter estimation method through algebraic computation only.However,this method cannot be applied before the induction motor reaches the steady state.

Furthermore,a parameteradaptive rotorflux observer was proposed in[7].In this method,a fullorderobserver was used whose order is 4 and the computation is timeconsuming.What is more important is that,it is not possible to set independently the convergence rates of the stator current and the rotor flux.

Moreover,in[8]a high performance flux observer with resistance adaptation was proposed.The problem with this method is that the degree of the control system is very high.A reduced order flux observer with stator resistance adaptation was introduced in[9],which uses the estimation error of back EMF(electromotive force)both in the flux observer and the resistance adaptation law.

1.4 This paper

As explained above,to achieve a high performance in the control of induction motors,parameter adaptation is desired.

An outstanding feature in motor control is that,for a good resistance adaptation it is better to slow down the estimation speed of stator current.Meanwhile,in DVC it is desirable to speed up the estimation speed of rotor flux for a good torque response.In a word,independent estimation of resistance and flux is desired in the vector controls of induction motors.However,such trade-off is impossible for a full order observer.

In this paper,a new parameter adaptation method for the stator and the rotor resistances and a new rotor flux observer will be proposed.The key idea is that,the flux reference is knownaprioriand the dynamics of stator current and rotor flux are decoupled when the flux is replaced by its reference in the dynamics of stator current.Hence,reduced order current and flux observers can be built.In the proposed method,the current observer can be tuned to a slow response while the flux observer can be tuned to a fast response.Slow response of the current observer contributes significantly to the resistance adaptation,while fast response of flux observer contributes to the performance improvement of DVC of induction motors.The used information are the current and voltage of stator,the reference of rotor flux and the rotor speed.

Furthermore,in the application to IdVC only the statorcurrentobserverand resistance adaptation algorithm are used which yields a simpler vector control structure.Meanwhile,in the application to DVC a faster and robustresponse can be achieved because the convergence ratesofcurrentand flux observerscan be tuned independently.The proposed adaptive vector control methods are investigated via numerous simulations.It is verified that the performance is significantly improved even in the low torque and low speed range.

In this paper,the estimates of both the state and the parameter are described by hatted notations such asˆx,the reference of a signalxis described byx∗.

2 Models of induction motor

In this paper,the scripts of different frames are omitted in the vectors of physical variable in order to simplify the notation.They are explicitly stated in the models below.The notations are standard and listed in Table 1 for the ease of reference.

Table 1 Notations.

2.1 Model in the d-q frame

Taking the stator currents and rotor fluxes as the states,the model of an induction motor in thed-qframe is described by

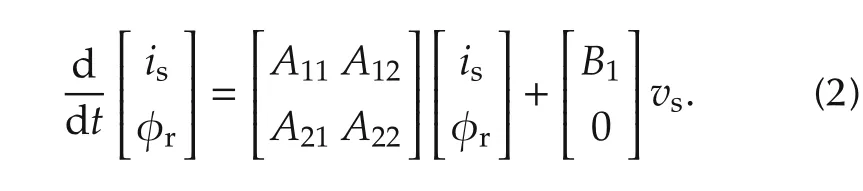
Here,the stator current vector is,rotor flux vector φrand stator voltage vector vsare given by

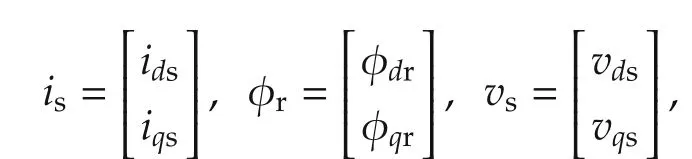
respectively.Furthermore,the coefficient matrices are

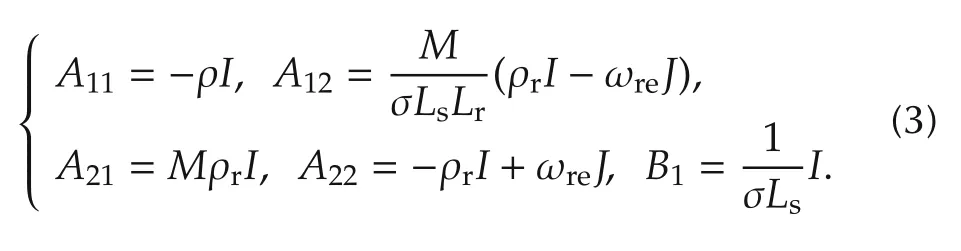
Furthermore,

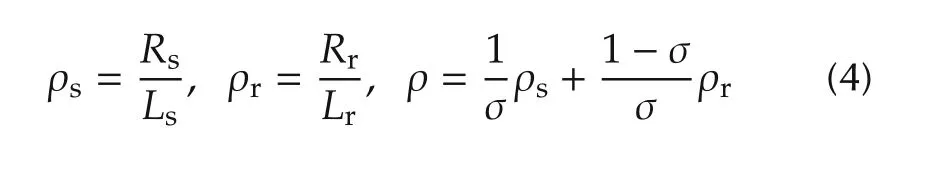
denote the ratios of resistance to inductance.In particular,ρsand ρrare the inverse time constants of the stator and rotor circuits.Moreover,

Since the rotorflux in the d-q frame is used to calculate the phase angle which is used in the frame transformation in DVC(refer to Fig.2),this model is used in the application to DVC and the associated flux observer.

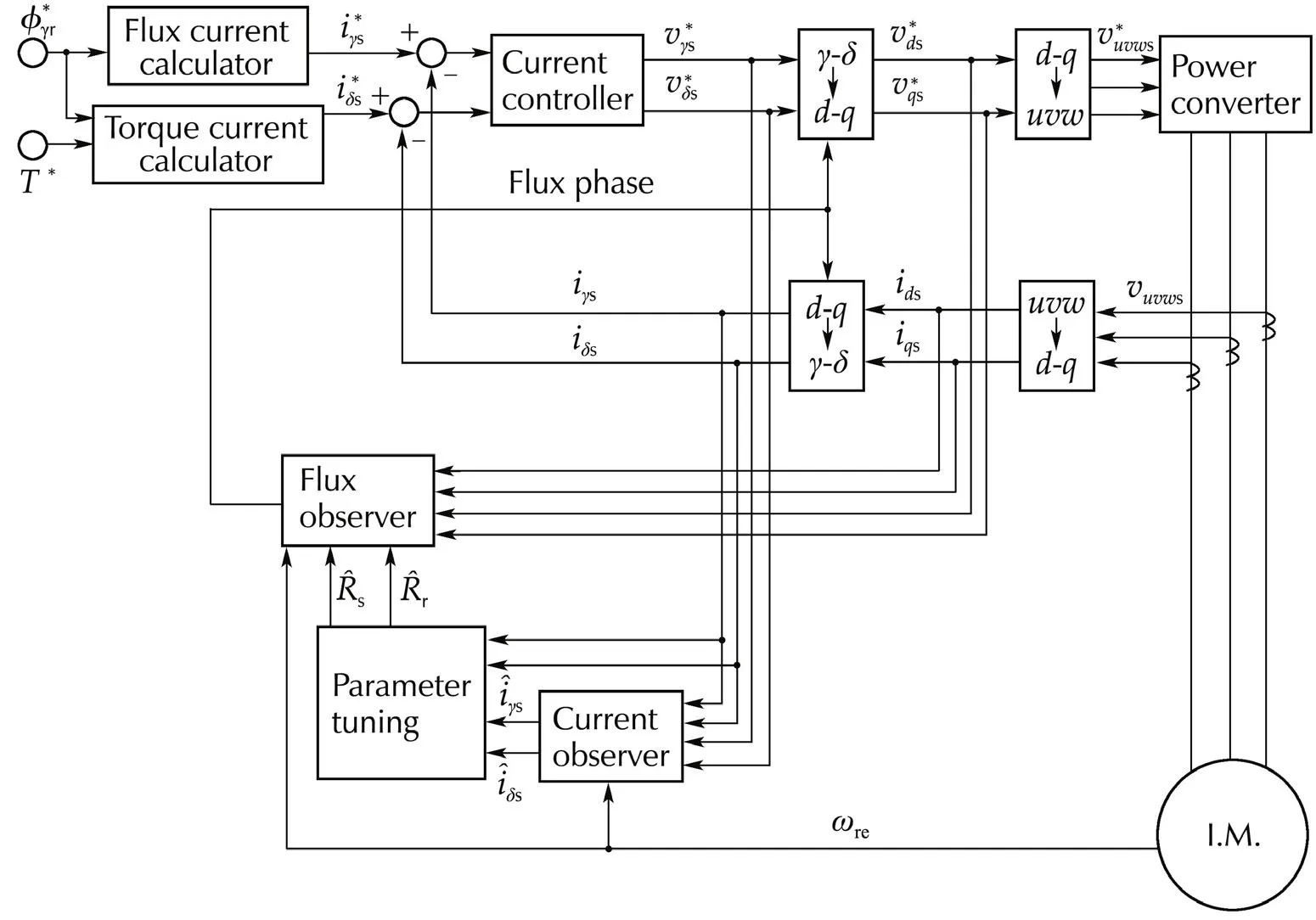
Fig.2 DVC system with the proposed estimation method.

2.2 Model in the γ-δ frame

Meanwhile,in the γ-δ frame the model of stator current isand rotor flux φris described by

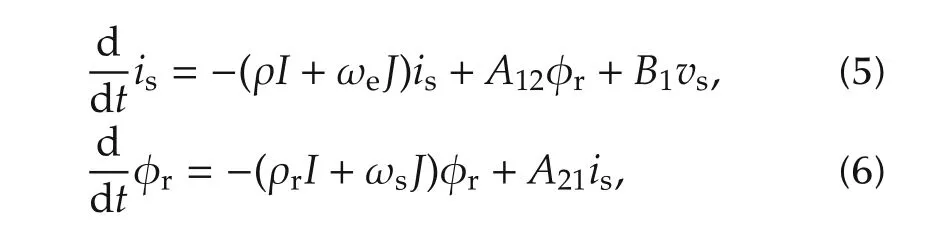
in which the stator current is,rotor flux φrand stator voltage vsare respectively

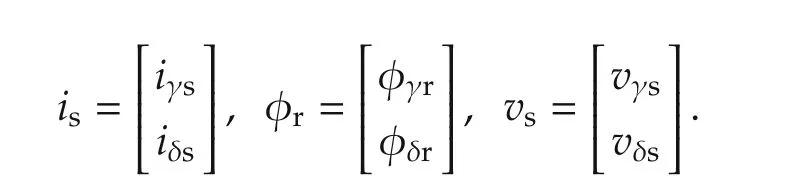
The current control is carried out in the γ-δ frame,and so this model is used in the resistance adaptation as well as the associated stator current observer.

3 Simplified parameter adaptation

Owing to(5),the stator current observer used for the adaptation ofparametersρr,ρsis constructed as follows:

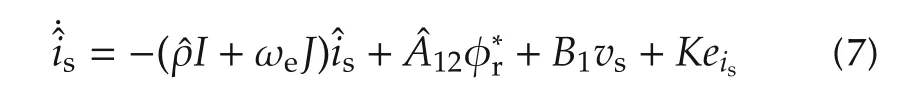
based on the model in γ-δ frame.Here,

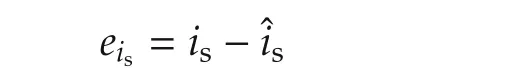
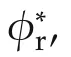
Let the tracking error of the rotor flux be

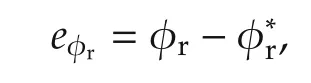
then the equation aboutthe estimation errorofthe stator current is given by

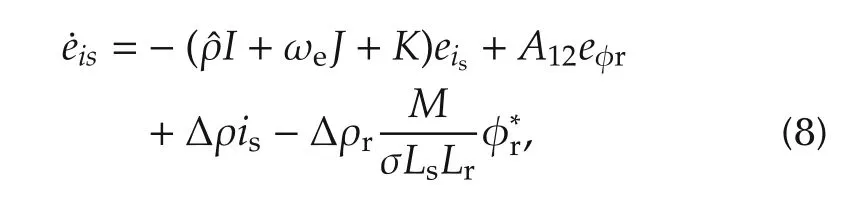
in which

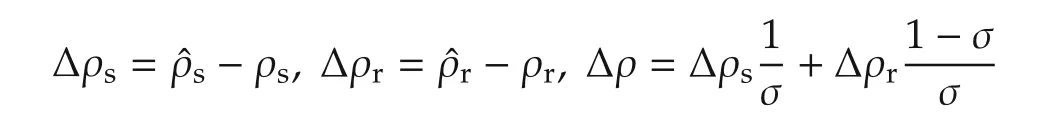
are the adaptation errors of the parameters.

To derive an adaptation law for the parameters(ρs,ρr),we use the following Lyapunov candidate:

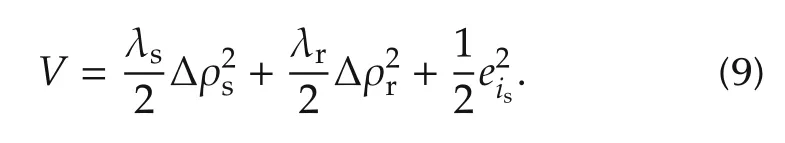
Here,λsand λrare the gains used for tuning of the convergence rate of parameter adaptation.Differentiation of this function along the trajectory and substitution of(8)yields

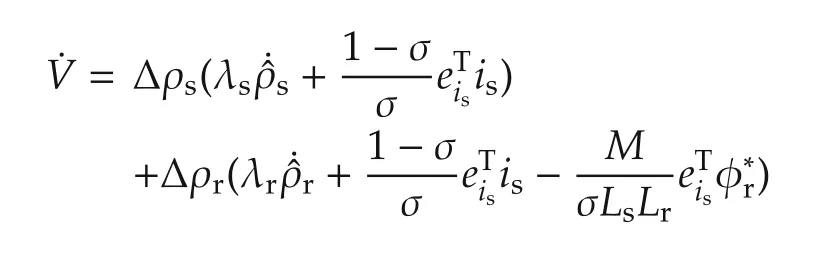
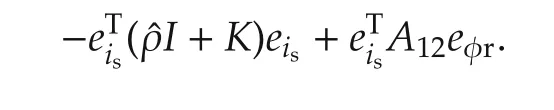
The adaptation law is determined as

The first term is negative definite while the second term is indefinite.It has been verified the parameter adaptation works well except in the regeneration mode of induction motor,similar to[7].

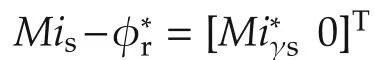
4 Rotor flux observer

As is clear from the rotor flux model(2)in the d-q frame,the convergence rate cannot be changed if we directly use it to estimate the rotor flux.Here an idea based on the minimal order observer is adopted in order to accelerate the convergence of flux estimation.Concretely speaking,a new state

is estimated instead by using the information of stator currentis,as described below:

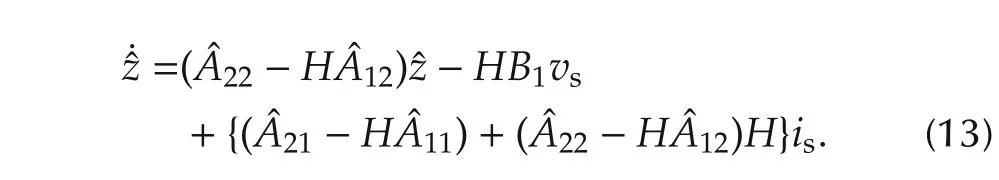
Here,the 2×2 matrix H is the observer gain.

Next,to analyze the convergence of flux estimation and the effect of parameter uncertainty,the estimation error

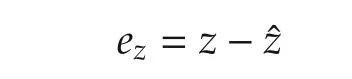
is defined.The error equation is easily obtained as

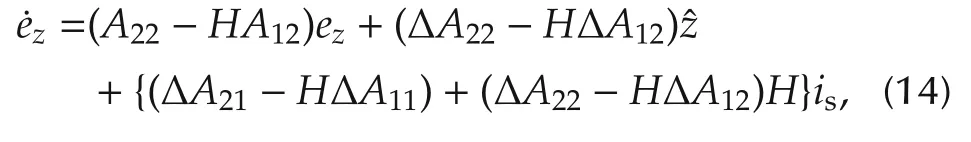
in which ΔAij=Aij−ˆAij.

In the open-loop case(i.e.,H=0),the observer dynamicsisgoverned by A22= −ρrI+ωreJ and itsresponse is extremely oscillatory even in the rated operation because ωre≫ ρr.To alleviate this oscillation,we propose using the following observer gain to reduce the oscillation frequency:

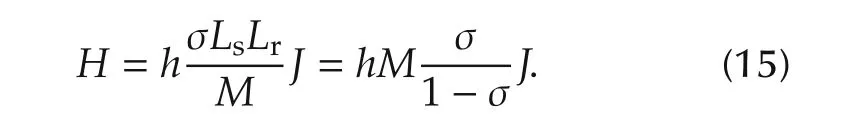
This gain H is a function of scalar h,and so the tuning is simple.

Concrete calculation shows that(14)can be written as

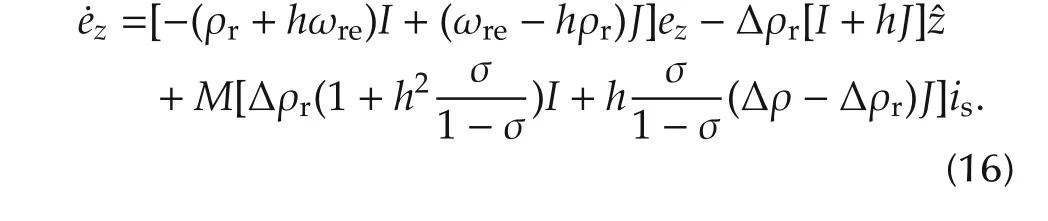
DiscussionThe 2nd and 3rd terms on the right side of(16)represent the effect of parameter error.When both Δρsand Δρrare made small enough via fast parameter adaptation,their influence is limited.

Meanwhile,the 1st term on the right side dominates the dynamic response of the flux observer.Since the convergence rate is−(ρr+hωre)and the oscillation frequency is ωre− hρr,increasing h leads to a fast convergence while setting h close to ωre/ρrreduces the oscillation.Hence,it is suggested to set h≈ ωre/ρr,i.e.,it is better for the observer gain to vary with the motor speed.In practice,as the true value of parameter is unknown,we suggest using

5 Application to vector controls

The proposed current observer and resistance adaptation law are incorporated into the standard IdVC configuration in Fig.1 which is composed of a PI-PWM,a slip frequency control and a parameter adaptation law.Concretely speaking,the estimated rotor resistance is used in the computation of the slip frequency.

On the other hand,the proposed flux and current observers and the resistance adaptation law are incorporated into the standard DVC configuration as shown in Fig.2 which is composed of PI-PWM controller,flux/current observers and parameter adaptation law.

MATLAB is used in the simulation.The parameters of the induction motor are listed in Table 2 which come from a motor in our lab.

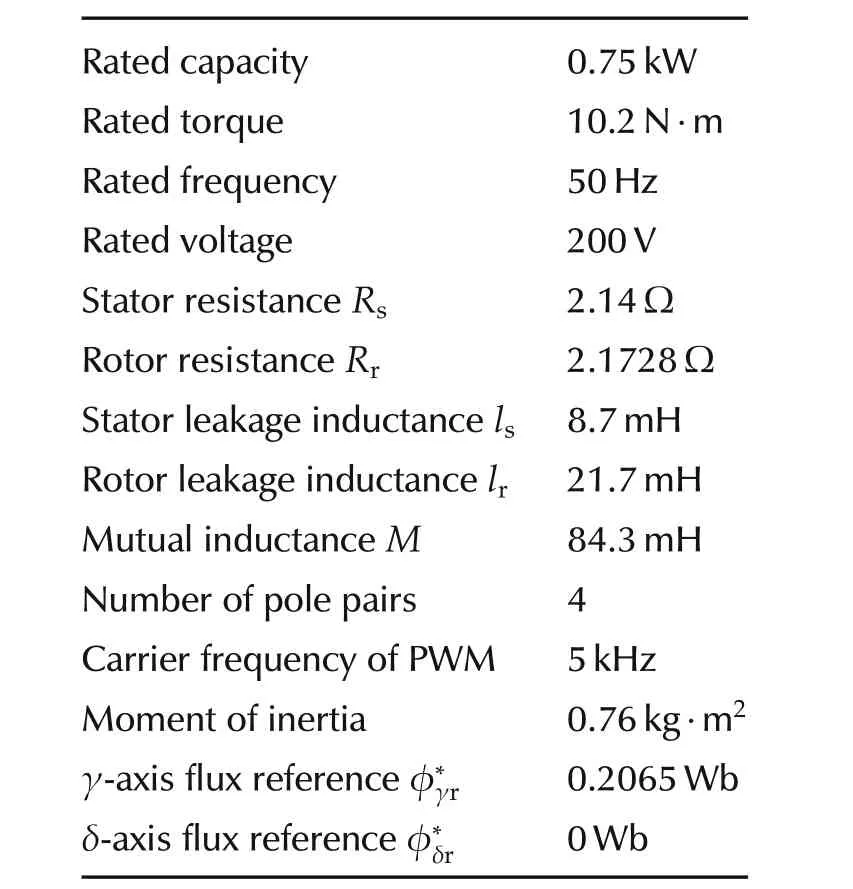
Table 2 Simulation parameter.

The reference torque is shown by a dotted line in all torque responses.Other simulation conditions are set as follows:

.The magnetic excitation current is a constant.

.The angular velocity is a constant.

.The dead time of inverter is ignored.

Simulations are carried out with respect to two scenarios:

1)Rated case:ωrm=700 r·min−1,T∗=10 N·m;

2)Low torque and low frequency:ωrm=70 r·min−1,T∗=1 N·m.

Since in general the control is much more difficult at low speed and low torque situation,case 2)is used to test the capability limit of proposed control methods.

6 Results of adaptive DVC

The adaptation gains are set as λs= λr=1/4.The initial values of resistances are set asˆρs(0)=0.8ρs,ˆρr(0)=0.8ρrwhich account for a 20%parameter error.Hereafter, φγr_est, φδr_estin the figures indicate the fluxes estimated by the flux observer,i.e.,ˆφγrandˆφδr.

The following three cases are shown in order to investigate the effect of the gains of current and flux observers.

1)Case 1:h=0,K=0(w/o correction terms in both observers).

2)Case 2:h=ωre/ˆρr(0),K=0(with correction term in the flux observer only).

3)Case 3:h=ωre/ˆρr(0),K=−67(current observer with a slower convergence rate).

In Case 1,the motor dynamics is directly used to estimate the current and flux which is usually used in practice.In Case 2,a current correction term is putted into the flux observer to improve the response of flux estimate.Comparison of these two cases illustrates the capability of the flux observer.Furthermore,the convergence rate of the current estimation is slowed down in Case 3 so as to validate the capability of the current observer in improving the parameter adaptation.

The resistance estimation starts att=2 s.The responses of torque,flux as well as the parameter estimates are shown in Figs.3–8.Shown in the figures of parameter estimates areˆRs/RsandˆRr/Rr,the ratios of estimated value and true value.Therefore,1 implies that the estimate coincides with the true value.

In all simulations,it is seen that before the parameter adaptation there is a big tracking error in the torque response due to the deviation of orientation in the estimated flux vector,which is caused by uncertainty in the motor parameters.

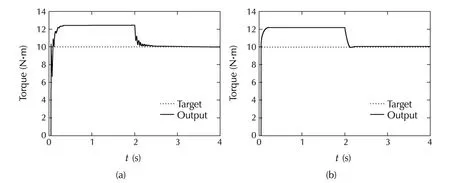
Fig.3 Torque response(DVC:700 r·min−1,10 N·m).(a)h=0,K=0.(b)h=14.3,K=0.

Fig.4 Flux response(DVC:700 r·min−1,10 N ·m).(a)h=0,K=0.(b)h=14.3,K=0.

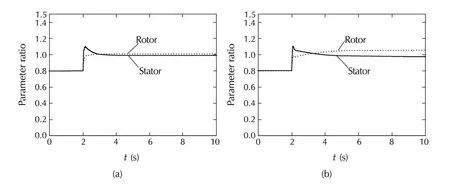
Fig.5 Parameter estimates(DVC:700 r·min−1,10 N ·m).(a)h=0,K=0.(b)h=14.3,K=0.

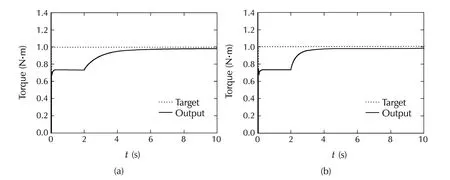
Fig.6 Torque response(DVC:70 r·min−1,1 N·m).(a)h=1.43,K=0.(b)h=1.43,K= −67.

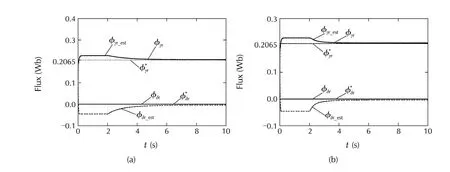
Fig.7 Flux response(DVC:70 r·min−1,1 N·m).(a)h=1.43,K=0.(b)h=1.43,K= −67.

Fig.8 Parameter estimates(DVC:70 r·min−1,1 N·m).(a)h=1.43,K=0.(b)h=1.43,K= −67.

Discussion

1)Rated case.

Due to the effect of parameter adaptation(Fig.5(a))the estimated rotor flux converges to the true flux(Fig.4(a))in the steady state.As a result,the steady state value of the torque tracks the reference well(Fig.3(a)).However,in the transient the flux(ˆφδrin particular)responds quite oscillatory,which causes oscillation in the torque.This is because the open-loop flux observer has a rather weak damping in the rated speed range.

This oscillation is suppressed efficiently by the introduction of the correction term(15)in the flux observer which strengthens the damping(Fig.4(b)and Fig.3(b)).However,the correction term in the flux observer has a negative effect on the parameter adaptation(Fig.5(b)).As is wellknown,excitation ofthe signalused in parameter adaptation contributes to the convergence of parameter estimation.In fact,persistent excitation is required for the asymptotic convergence of parameter estimate.However,the oscillation of flux estimate is eliminated by the correction term.In this sense,certain degree of oscillation should better be retained in the flux observer and the current observer as well.

2)Low torque and low speed case.

In this case,the negative influence of the correction term in flux observer is more serious.Both the torque response and the flux response get rather slow(Fig.7(a)and Fig.6(a)).However,a positive feedback in the current observer improves the convergence of parameter adaptation(Fig.8(b)),which yields improved flux and torque responses(Fig.7(b)and Fig.6(b)).In fact,the gain of current observer is chosen as such that moves the observer poles close to the imaginary axis(the openloop poles are around−67).

3)Tuning of adaptation gain.

As has been remarked,in the low speed operation the torque component of stator current(iδs)decreases which has a negative effect on the parameter adaptation.To overcome this difficulty,smaller gains are tried(λs= λr=0.1).The corresponding results are shown in Fig.9.It is obvious that the convergence of parameter adaptation gets faster.As a result,both flux and torque respond quickly.

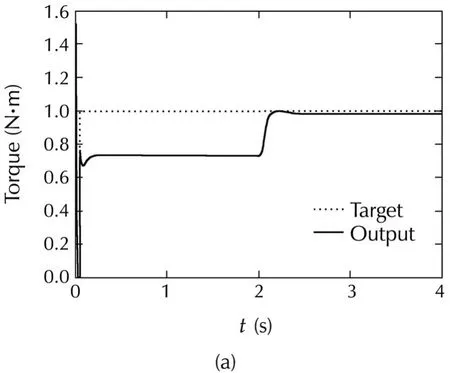
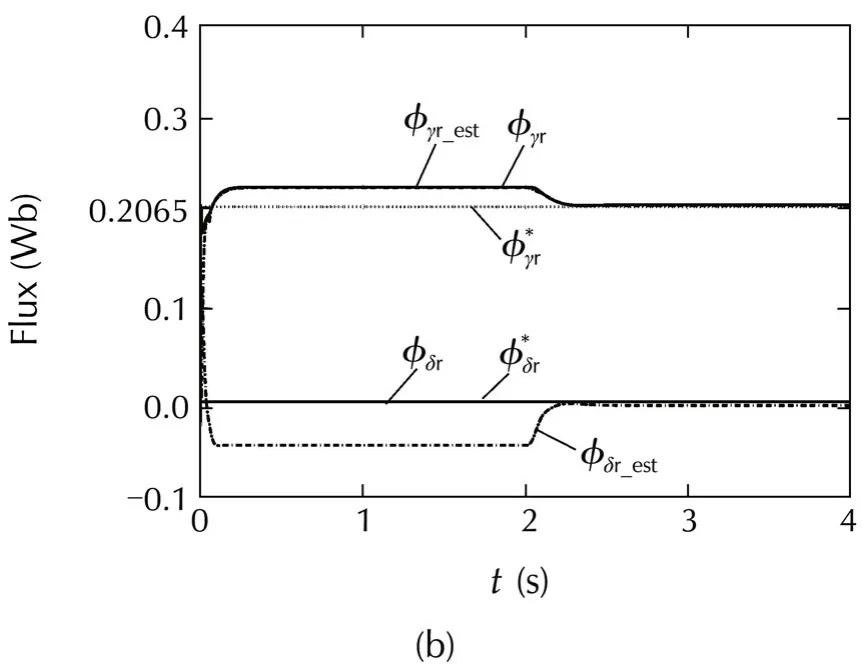
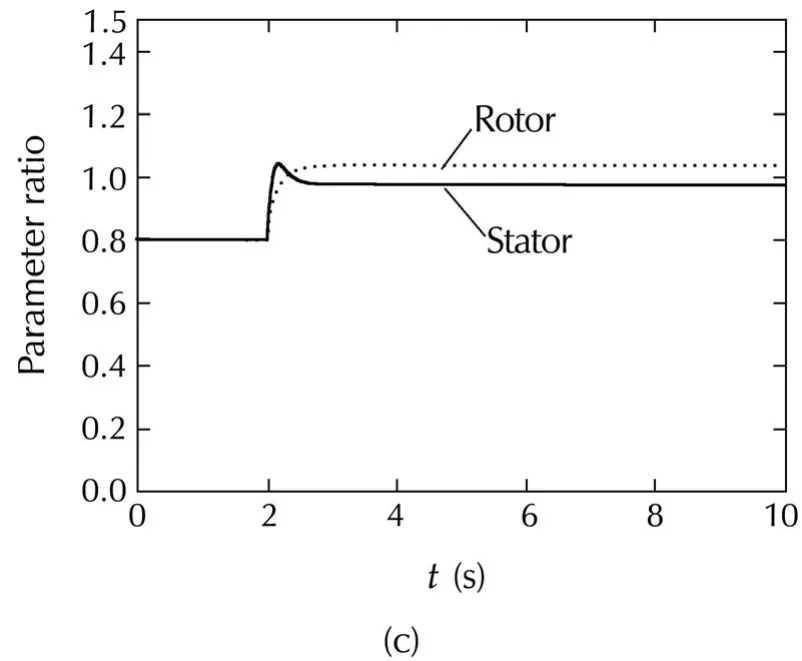
Fig.9 Responses of DVC(70 r·min−1,1 N·m:λs= λr=0.1).(a)Torque.(b)Flux.(c)Parameter estimates.

7 Results of IdVC

The torque reference is set as 1 N·m up to 0.8 s in order to build the necessary rotor flux.After that,it is switched to the assigned valueT∗.The initial values ˆRr(0),ˆRs(0)of the parameter estimates and the adaptation gains λs,λrare set the same as in the DVC simulations.The parameter adaptation starts att=2 s.

The torque and the flux responses are shown in Fig.10 and Fig.11.It can be seen that both the torque and the rotor flux track their references satisfactorily.Furthermore,the parameter adaptation works well over a wide range from the rated speed and rated torque(Fig.10)to 10%of the rated values(Fig.11).

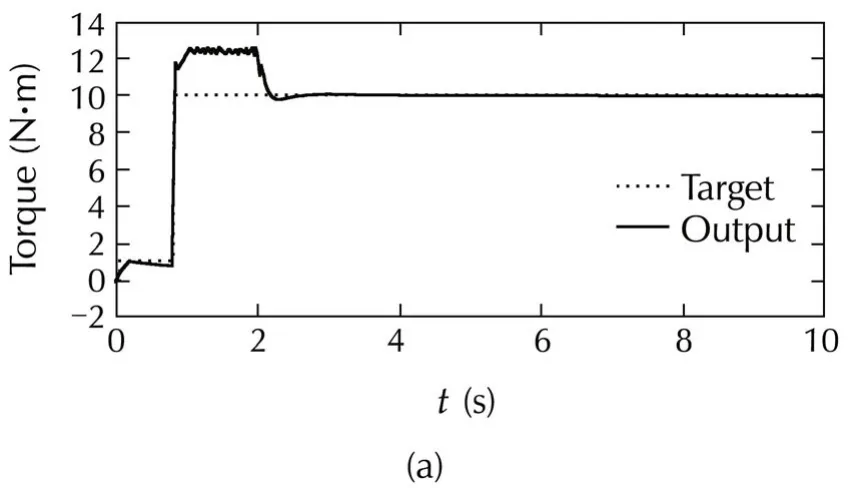
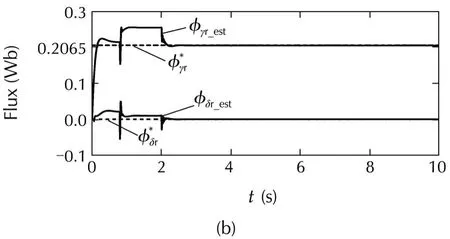
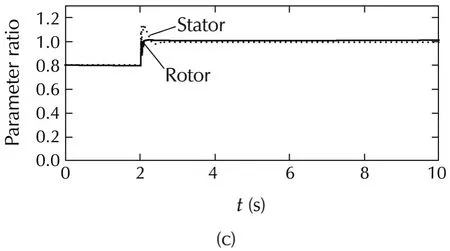
Fig.10 Response of IdVC(700 r·min−1,10 N·m).(a)Torque.(b)Flux.(c)Parameter adaptation.

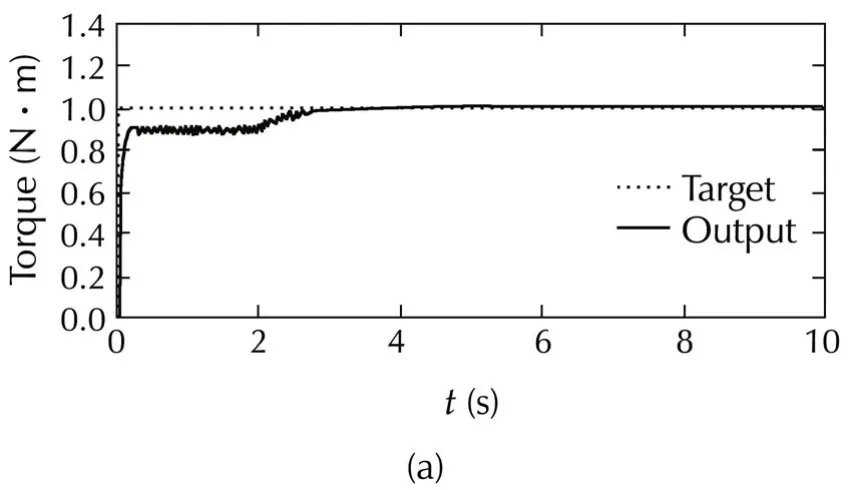
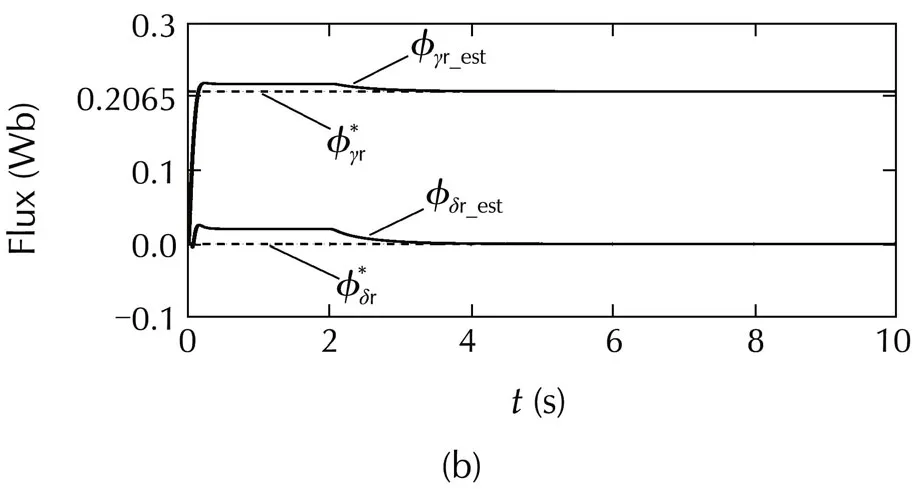
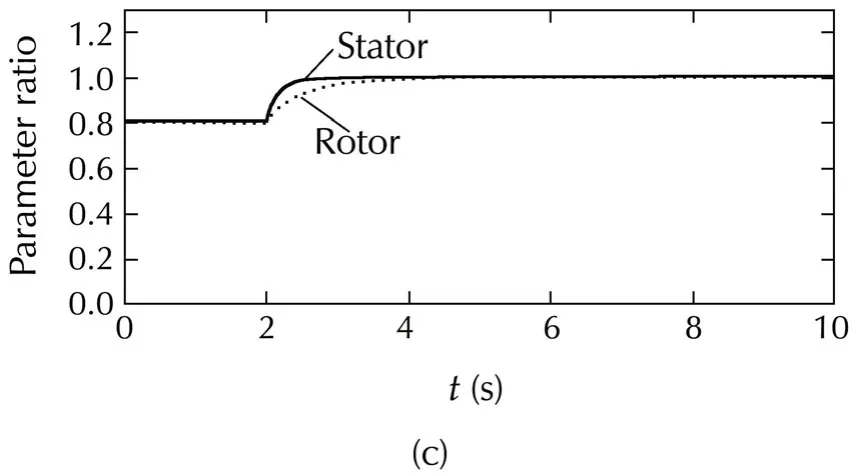
Fig.11 Response of IdVC(70 r·min−1,1 N ·m).(a)Torque.(b)Flux.(c)Parameter adaptation.

8 Conclusions

In this paper,an independent estimation method has been proposed for the estimation of resistance and rotor flux based on decoupled current and flux observers.Furthermore,the guideline for the selection of observer gains as well as the adaptation gains has also been ex-posed.The proposed method shows a high performance when applied to the vector controls,including both direct and indirect,of induction motors.This method has the following outstanding features:1)the performance is quite good since fast convergence of resistance and flux can be achieved simultaneously to certain degree by slowing down the convergence rate of current observer while speeding up that of the flux observer;2)it has a very simple structure and is easy to implement because the order of the observers and adaptive law are minimal.

[1]B.K.Bose.Modern Power Electronics and AC Drivers.Upper Saddle River:Prentice Hall,2001.

[2]G.C.Verghese,S.R.Sanders.Observers for flux estimation in induction machines.IEEE Transactions on Industrial Electronics,1988,35(1):85–94.

[3]P.L.Jansen,R.D.Lorenz.A physically insightful approach to the design and accuracy assessment of flux observers for field oriented induction machine drives.IEEE Transactions on Industry Applications,1994,30(1):101–110.

[4]H.Sugimoto,S.Tamai.Secondary resistance identification of an induction-motor appplied model reference adaptive system and its characteristics.IEEE Transactions on Industry Applications,1987,23(2):296–303.

[5]I.J.Ha,S.H.Lee.An online identification method for both stator and rotor resistances of induction motors without rotational transducers.IEEE Transactions on Industrial Electronics,2000,47(4):842–853.

[6]C.C.Chan.An effective method for rotor resistance identification for high-performance induction motor vector control.IEEE Transactions on Industrial Electronics,1990,37(6):477–482.

[7]H.Kubota,K.Matsuse.Adaptive flux observer of induction motor and its stability.Transactions of the Institute of Electrical Engineers Japan–Part D,1991,111(3):188–194(in Japanese).

[8]S.H.Jeon,K.K.Oh,J.Y.Choi.Flux observers with online tunning of stator and rotor resistances for induction motors.IEEE Transactions on Industry Applications,2002,49(3):653–664.

[9]M.Hinkkanen,L.Harnefors,J.Luomi.Reduced-order flux observers with stator-resistance adaptation for speed-sensorless induction motor drives.IEEE Transactions on Power Electronics,2010,25(5):1173–1183.

Kang-Zhi LIUis a professor at the Department of Electrical and Electronic Engineering,Chiba University.He graduated from Northwestern Polytechnical University,China in 1984 and received his Ph.D.degree from Chiba University in 1991.He has authored and co-authored five books.His recent research interests include system integration of smart-grid,power systems,nonlinear control and robust control theories.E-mail:kzliu@faculty.chiba-u.jp.

Masashi YOKOOgraduated from the Department of Electrical and Electronic Engineering,Chiba University in 2013,and is now a master course student at the department.His research interest is the control of motor drives.E-mail:myokoo@chiba-u.jp.

Keiichiro KONDOis a professor at the Department of Electrical and Electronic Engineering,Chiba University.He received B.Sc.and Ph.D.degrees from the Faculty of Electrical Engineering,Waseda University in 1991 and 2000,respectively.His research interests are power electronics,AC motor drive,energy storage system,wireless power transmission and their applications to the railway vehicle traction.E-mail:kkondo@faculty.chibau.jp.

Tadanao ZANMAis an associate professor at the Department of Electrical and Electronic Engineering,Chiba University.He received the B.Sc.,M.Sc.and Ph.D.degrees from Nagoya University in 1995,1997 and 2000,respectively.Hisresearch interestsinclude hybrid dynamical systems,especially,system control based on mixed logical dynamical systems and model predictive control.E-mail:zanma@chiba-u.jp.

†Corresponding author.

E-mail:kzliu@faculty.chiba-u.jp.Tel.:+81-43-290-3340;fax:+81-43-290-3340.

©2015 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg