Decentralized load frequency control for two-area interconnected power system

Wei WANG,Hiromitsu OHMORI

Department of System Design Engineering,Keio University,Kanagawa,Japan

Received 15 September 2014;revised 27 April 2015;accepted 27 April 2015

Decentralized load frequency control for two-area interconnected power system

Wei WANG†,Hiromitsu OHMORI

Department of System Design Engineering,Keio University,Kanagawa,Japan

Received 15 September 2014;revised 27 April 2015;accepted 27 April 2015

This paper proposes a decentralized output feedback control scheme applied to two-area interconnected power system.The controller synthesis problem is formulated as the scaled H∞control problem and a new LMI-based algorithm is proposed to compute the decentralized controller.The proposed controller provides robustness with regard to parametric uncertainties and also attenuates bounded exogenous disturbances in the sense of L2-gain.Simulation results clearly show the effectiveness of developed decentralized output feedback control scheme.

Power system,decentralized control,output feedback control,robustness,LMI

DOI 10.1007/s11768-015-4125-3

1 Introduction

For large-scale power system,which commonly consists of interconnected subsystems,the centralized control system is expensive to implement because of high communication cost and computational burden.

On the contrary,in the decentralized control system,each localcontrollerdetermines the controlaction based on the local measurement only.That is,the decentralized control is a more effective way to resolve issues of communication delay and data loss.

As a result,the decentralized control of large-scale power system has been paid much attention.

Recently,several decentralized control methods have been developed.Major ones are the overlapping control scheme[1]and the homotopy[2]method.

In[1],an overlapping control scheme is proposed to construct a decentralized state feedback control law for power system.A state feedback control system requires that all state variables are measurable and available.However,not all of the state variables are easily measured in practice.

In[2],the synthesis problem is reduced into the feasibility problem of nonlinear matrix inequality(NMI).The NMIs will be solved iteratively by the idea of homotopy.

This paper aims at developing a new decentralized output feedback control method for a two-machine power system.The closed-loop interconnected systemis equivalently represented as an interconnection of two closed-loop systems.Then,the synthesis problem is formulated as a scaled H∞control problem,and an LMI-based algorithm is proposed to compute the decentralized controller.

The proposed decentralized controller enhances the disturbance attenuation performance in the sense ofL2-gain.

Moreover,parameter uncertainties are taken into account in the controller design to achieve system robustness.The effectiveness of proposed method is verified by simulation results.

2 System description

In this section,we considera powersystem consisting of two machines connected by a tie line.

The swing equation for theith generator(i=1,2)is[3]

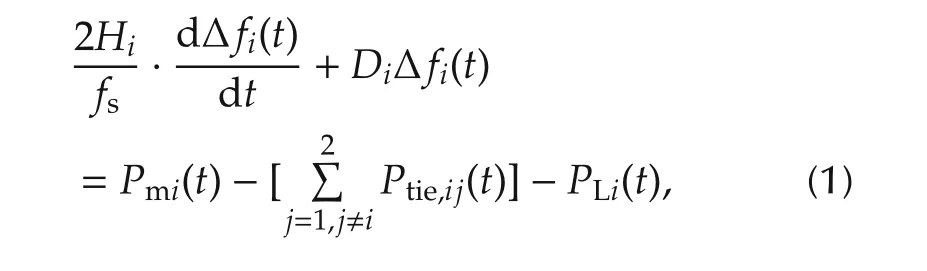
wherePmiis the mechanical input energy,PLiis the load disturbance,Ptie,ijis the tie line power flow directed from theith generator to thejth generator(j=1,2,j≠i),fsis the nominal frequency,Hiis the inertia constant,Diis the damping constant and Δfiis the frequency deviation.

We suppose that eachHisatisfies[4]

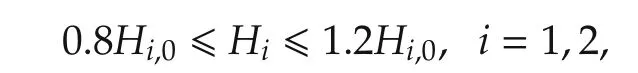
whereHi,0is the nominal value ofHi.

Neglecting the transmission loss,we can write the tie line power flow in the form[3]

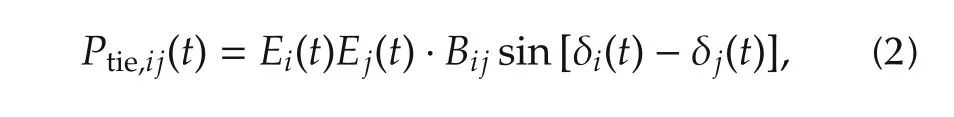
whereEiandE jare the terminal voltage magnitudes,Bijis the susceptance between theith andjth nodes,δiand δjare the power angles of corresponding generators.

The power angle δiis related to Δfi,and is given by

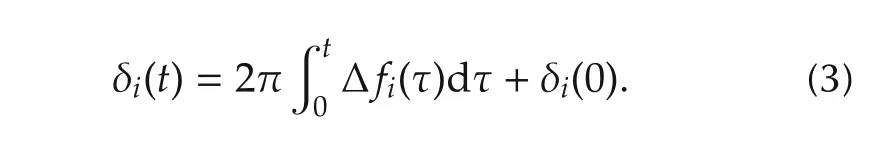
Since small variations in load are expected during normal operation,we make the following two assumptions[1].

Assumption 1Ei(t)≈Ei,0andE j(t)≈E j,0,whereEi,0andE j,0are the nominal values ofEiandE j,respectively.

Assumption 2Each δiis close to its reference value,i.e.,

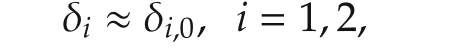
where δi,0is the reference value of δi.

The expression for the reference value ofPtie,ijis

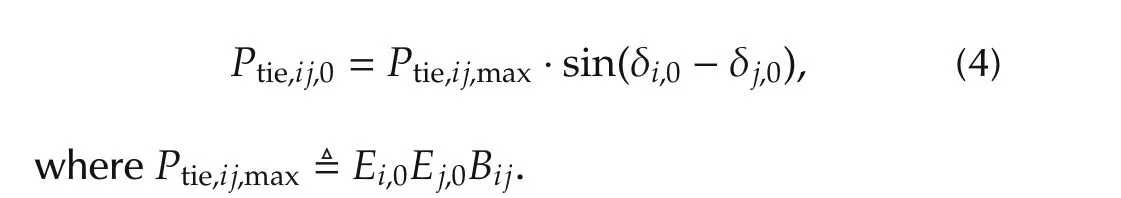
Under Assumption 1,the tie line powerflow deviation can be approximately expressed as

wherehij(t)=sin[δi(t)− δj(t)]− sin(δi,0− δj,0).

We use the trigonometric identities to expresshijas

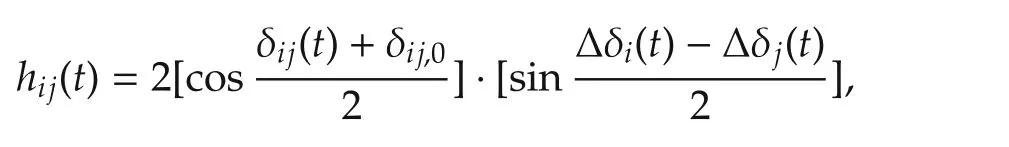
where δij(t)= δi(t)− δj(t)and δij,0= δi,0− δj,0.

Under Assumption 2,we obtain the approximation

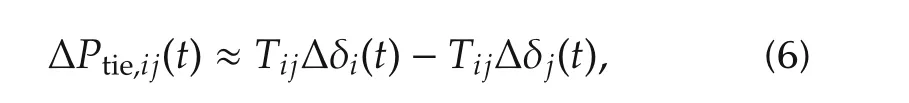
We suppose thatPtie,ij,maxsatisfies[4]

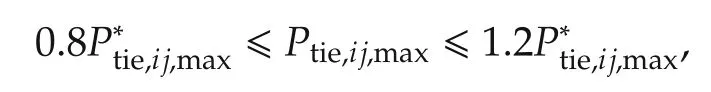
LetPLi,0denote the nominal value ofPLi.By performing simple algebraic manipulations,we have

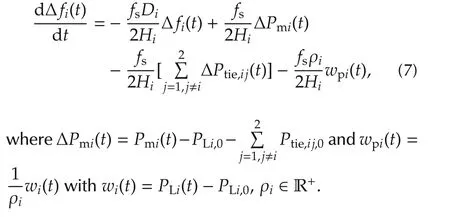
Without loss of generality,we assume the following condition on system(7).

Assumption 3wiand its variation rate are bounded,i.e.,there exist known positive scalarsdiandvisuch that

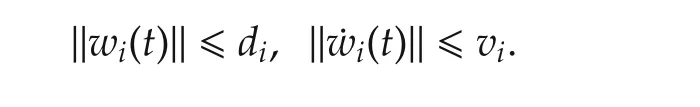
The turbine is assumed to be of the non-reheat type,and is modeled as[3]

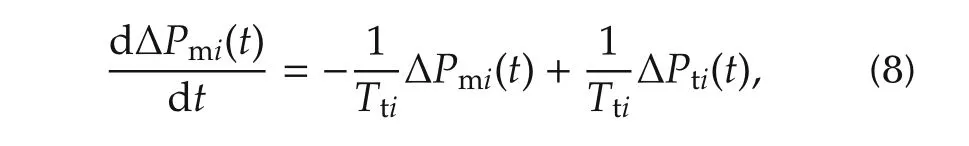
whereTtiis the turbine time constant,ΔPtiis the incremental change in value position.

The mechanical-hydraulic governor can be represented as the first order system[3]

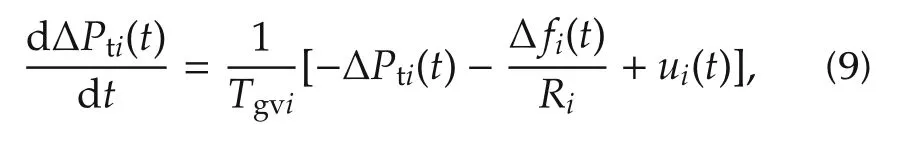
whereRiandTgviare the regulation constant and governor time constant,respectively,anduiis the control input.

By choosing the states for the first machine as

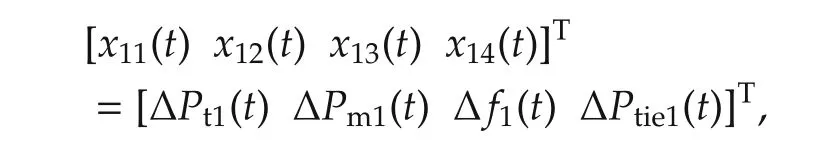
the dynamic model can be written in state-space form as

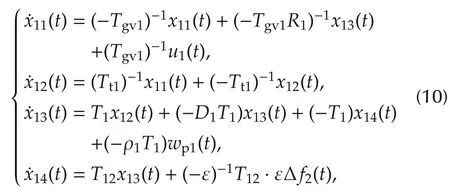
We choose the states for the second machine as

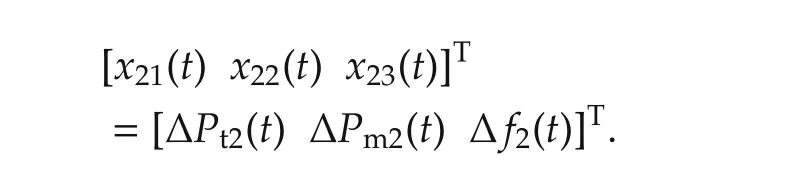
The dynamic modelofthe second machine is omitted.

3 Problem formulation

As illustrated in Fig.1,we can obtain the augmented plantGp1(θ1)by interconnecting weight functions withG1(θ1),which represents the plant corresponding to(10).

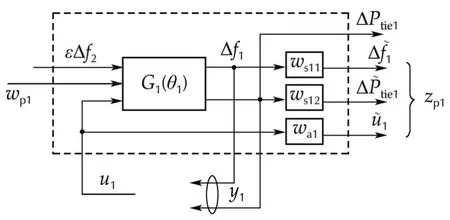
Fig.1 Block diagram of the generalized plant Gp1(θ1).

The augmented plantGp1(θ1)can be expressed as an LPV model

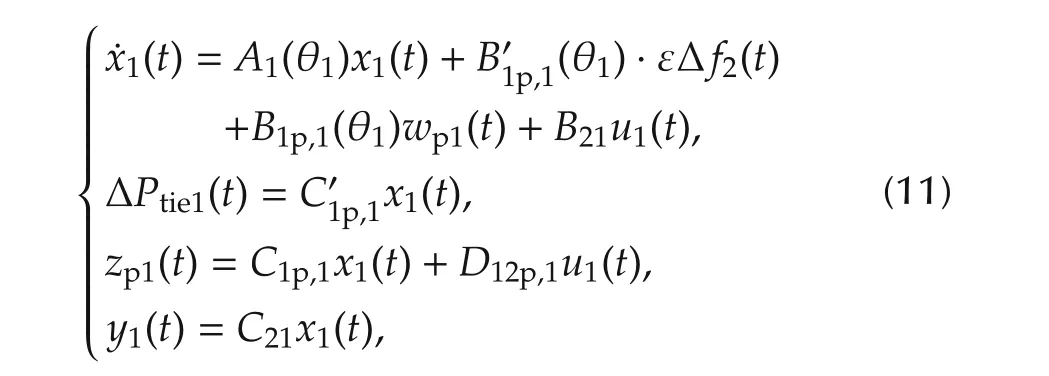
wherex1∈R7is the plant state vector and

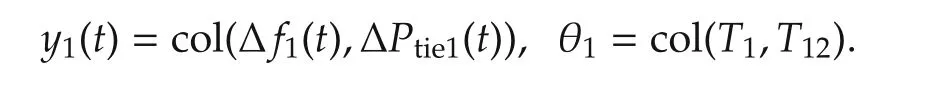
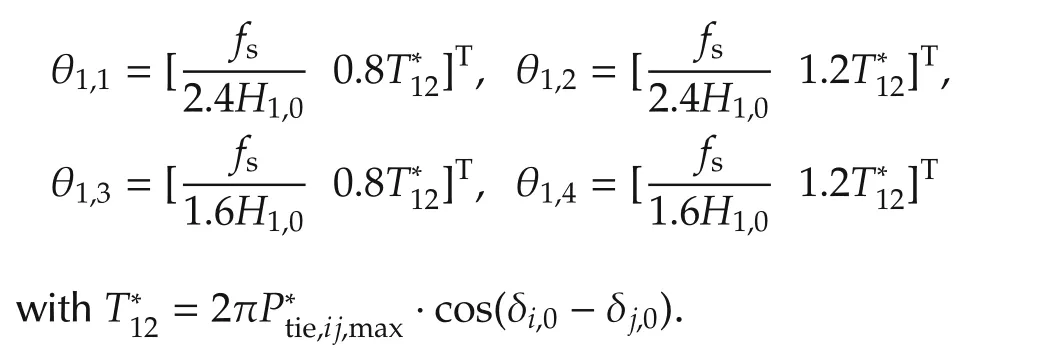
By normalization,T1can be written in the form

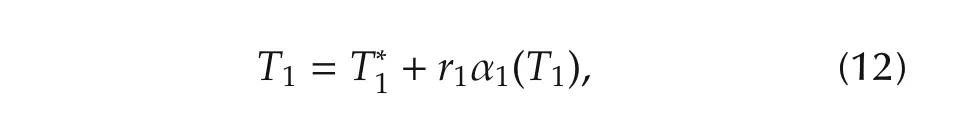
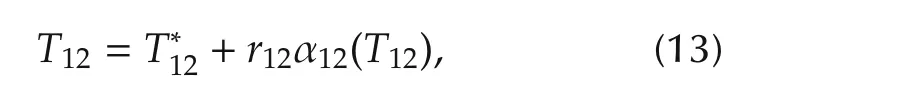
By substituting(12)and(13)into the matrixA1(θ1),and performing matrix decomposition,we have

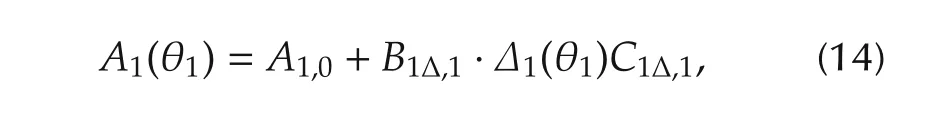
in whichA1,0indicates the matrix with respect to nominal values of uncertain parametersT1andT12.

Remark 1Δ1(θ1)has a block diagonal structure as

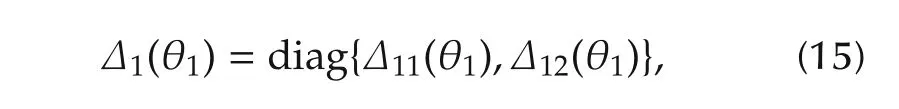
where Δ12(θ1)= α1(T1)I2and

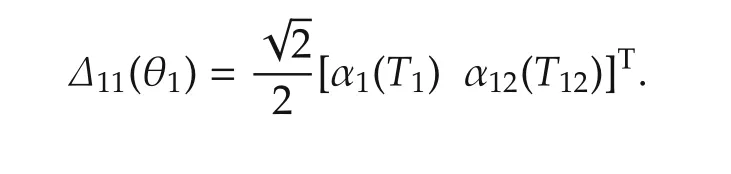
In view of(12)–(15),it follows that

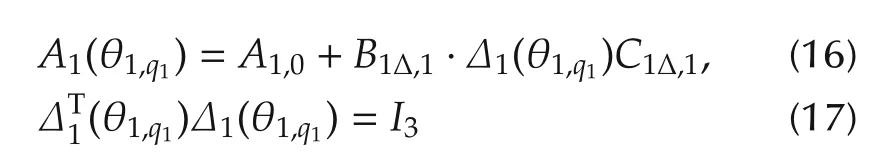
hold for allq1=1,...,4.

Substitution of(14)into the first equation of(11)yields

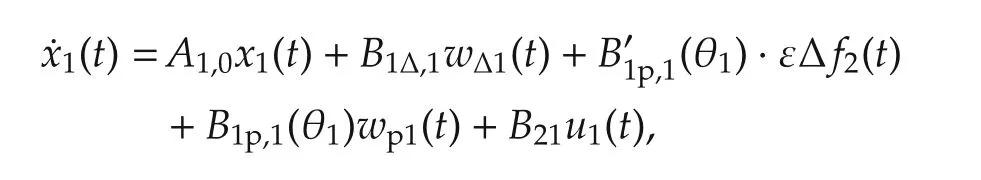
wherewΔ1(t)= Δ1(θ1)zΔ1(t),zΔ1(t)=C1Δ,1x1(t).

For the synthesis of static output feedback controller,the generalized plantGp1(θ1)is expressed as the interconnection of Δ1(θ1)with the nominal plant

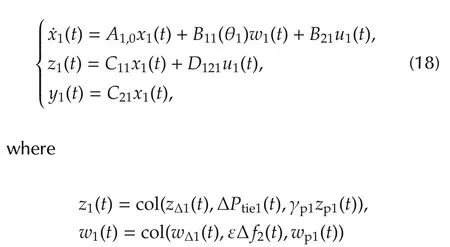
with γp1∈ R+.

The generalized plantGp2(θ2),shown in Fig.2,is applied to synthesize a controller for the second machine.We express the generalized plantGp2(θ2)as

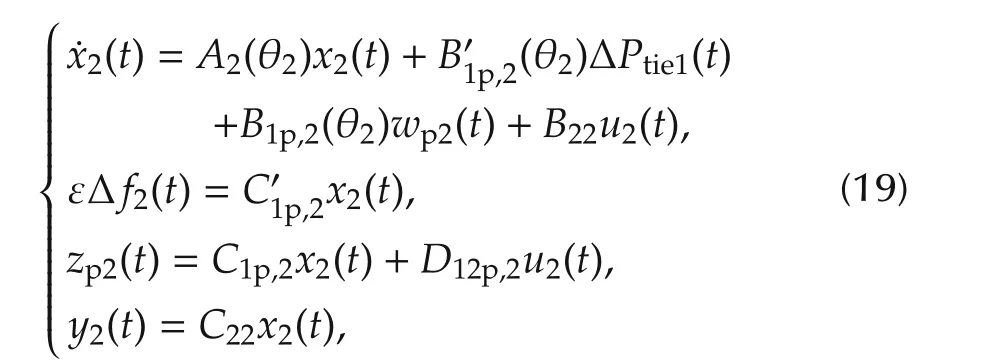
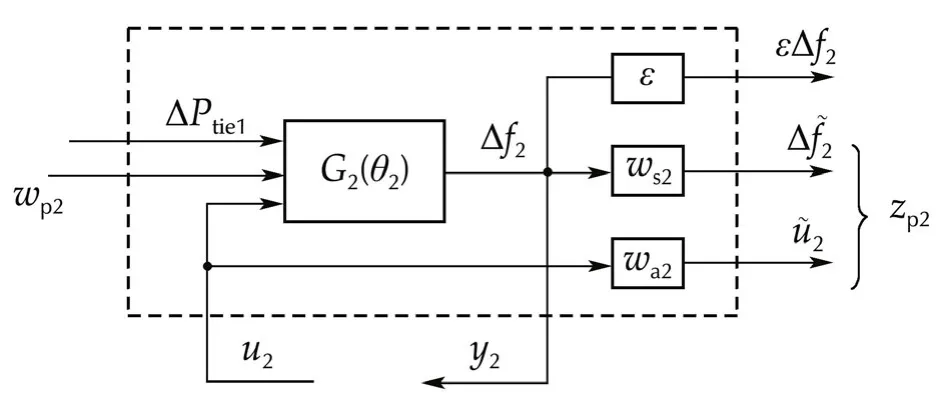
Fig.2 Block diagram of the generalized plant Gp2(θ2).

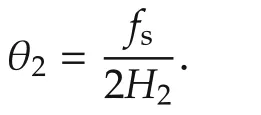
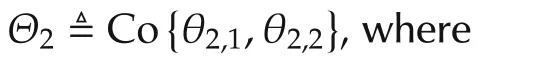
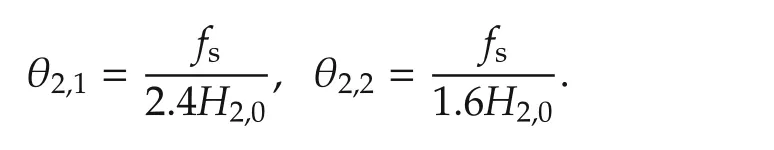
Problem 1The control task addressed in this paper is to find a static output feedback control law

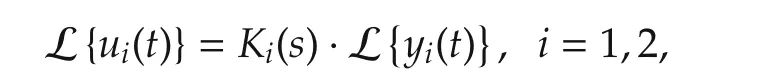
for the generalized plantGpi(θi),such that for a given positive value γ,the corresponding closed-loop interconnected system satisfies the following dissipation inequality:

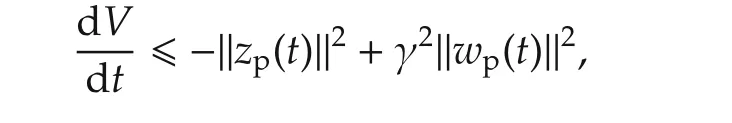
whereVis a nonnegative storage function and

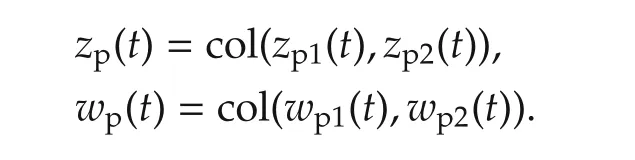
4 Decentralized controller synthesis

We willpropose an LMI-based iterative algorithm similar to DK-iteration method,for the synthesis of decentralized controller.The static output feedback controller synthesis for each subsystem will individually proceed.

4.1 Controller synthesis for the first machine

We start by setting the initial value ofg1to be 1.

Then,the initial guess for scaling matrices is given by

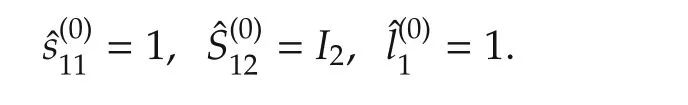
The general synthesis procedure involves three steps.

Step 1In theg1th iteration,we consider a strictly proper output feedback controllerK(g1)1(s)described by

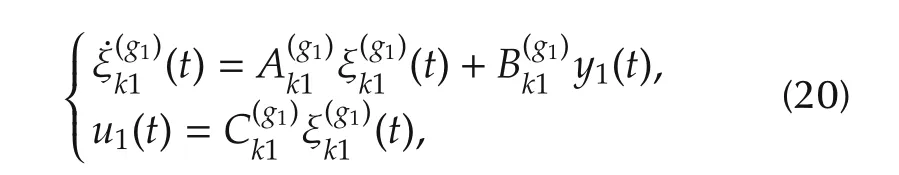
where ξ(g1)k1∈R7is the controller state vector.

Remark 2Superscript(·)denotes the iteration index.

We construct the following two scaling matrices:

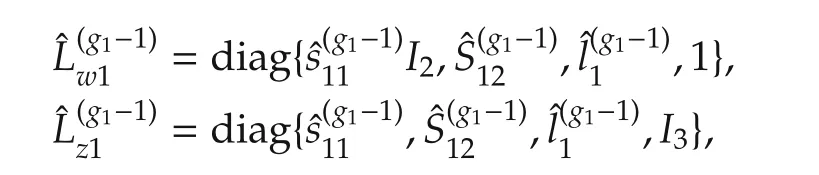
Remark 3We denote the set ofn×nsymmetric positive definite matrices by Sn++.

Combining(18)and(20)leads to

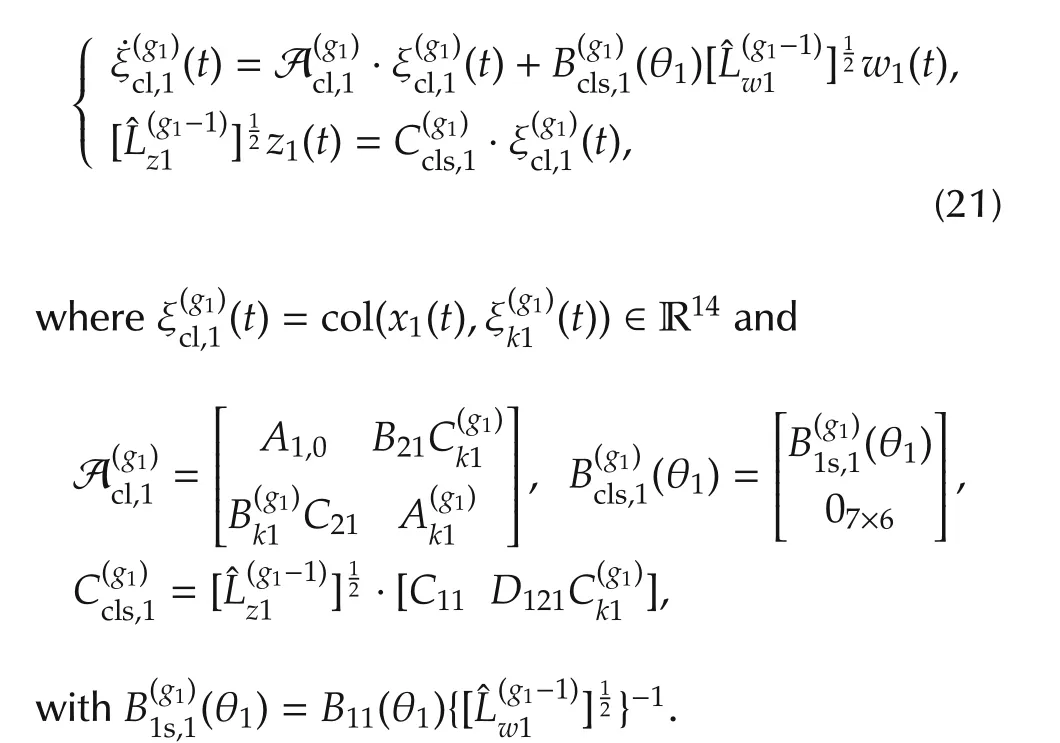
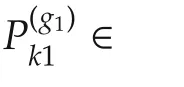
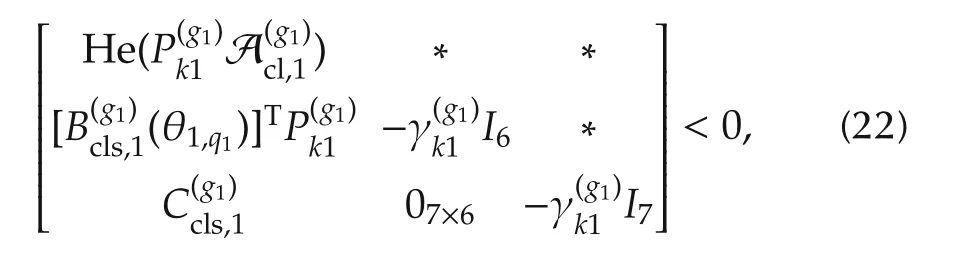
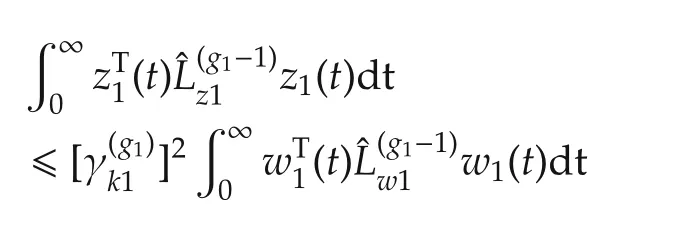
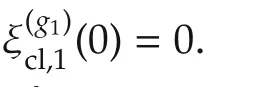
For simplicity,∗denotes the symmetric item in a symmetric matrix and He(Λ)= ΛT+Λ.

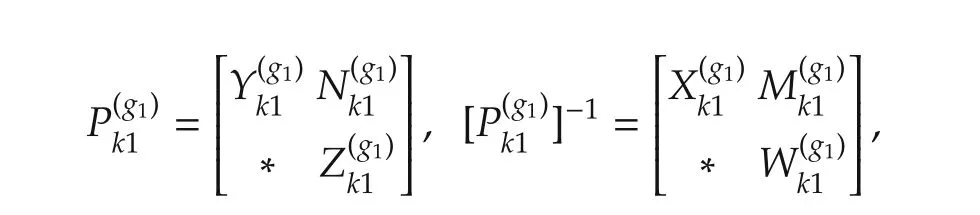
have

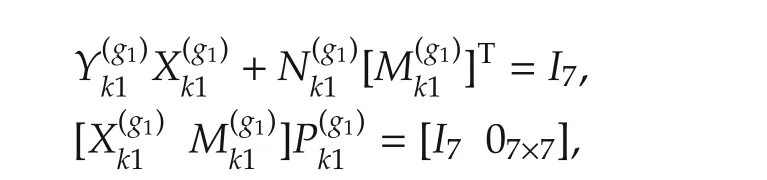
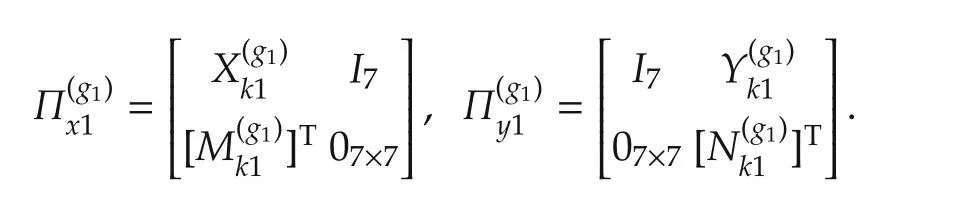
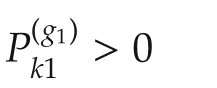
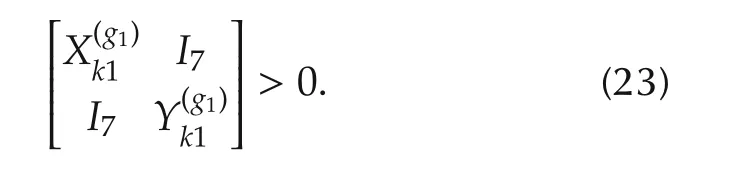
Meanwhile,by performing a congruence transformation on(22)with diag{Π(g1)x1,I6,I7},we have

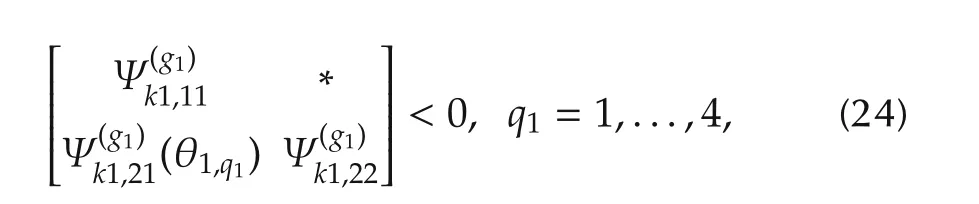
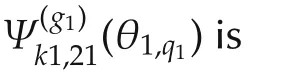
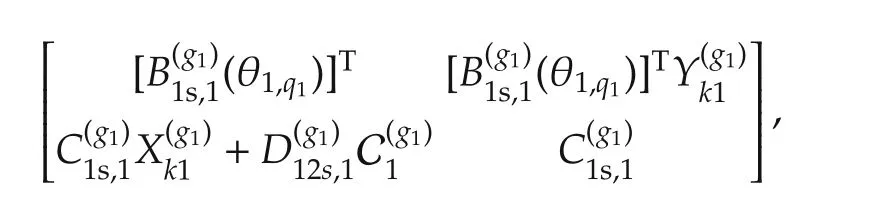
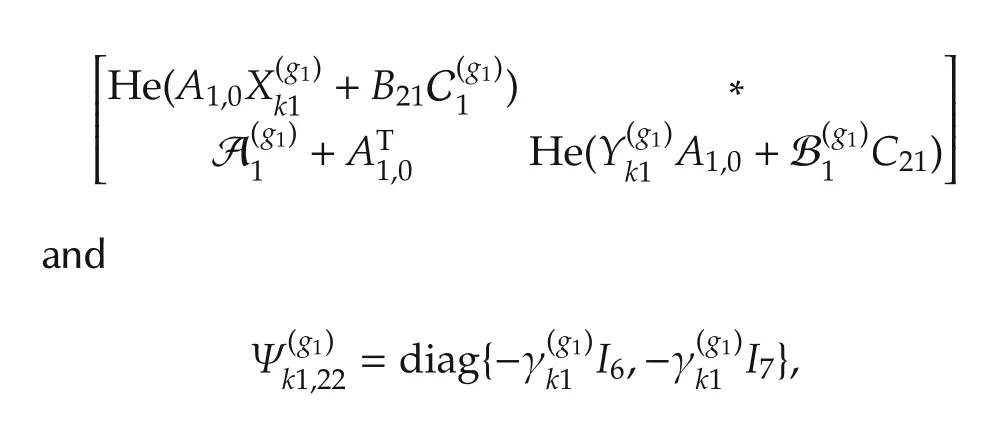
The auxiliary variables are defined as[5]

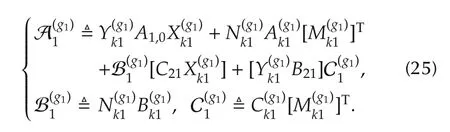
Note that all auxiliary variables are independent of θ1,q1.

In summary,the LMI optimization problem is

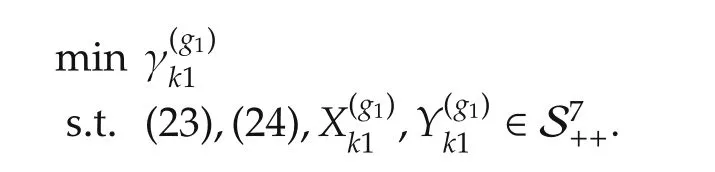
The set of optimal solutions is denoted by

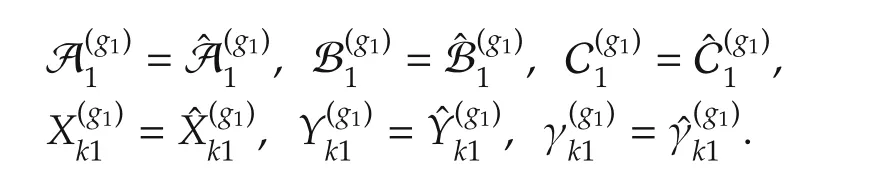
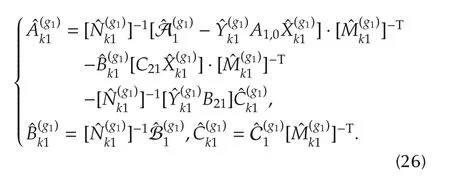
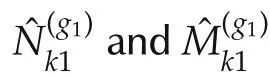
Step 2Let us consider scaling matrices of the form

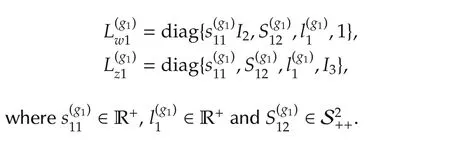
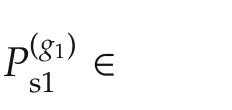
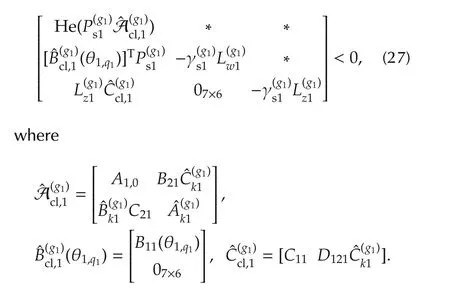
The bisection method is used to solve the following optimization problem:

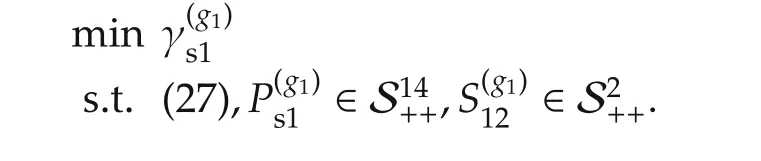
The set of optimal solutions is denoted by

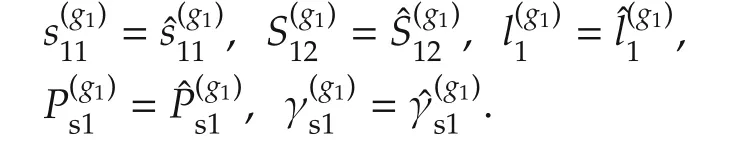
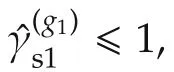
Through trial and error,we choose the design parameters as ε =0.5,γp1=1.61 and ρ1=0.01.

For convenience,we denote

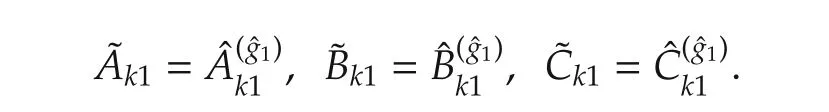
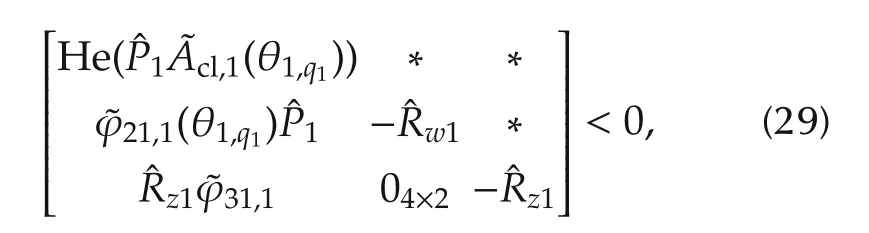
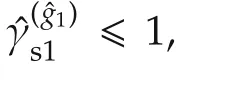
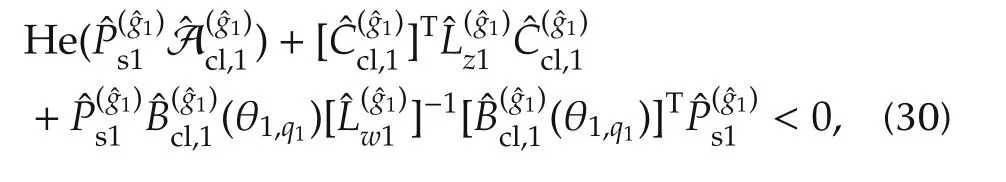
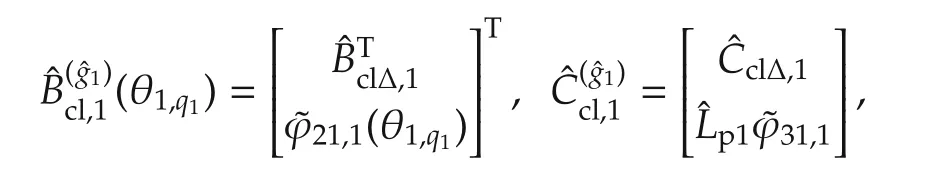
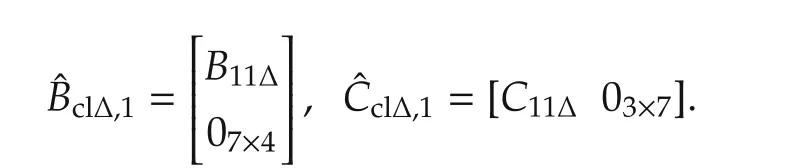
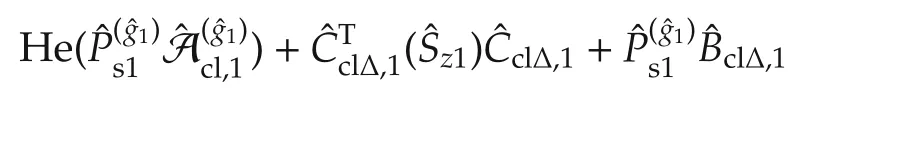
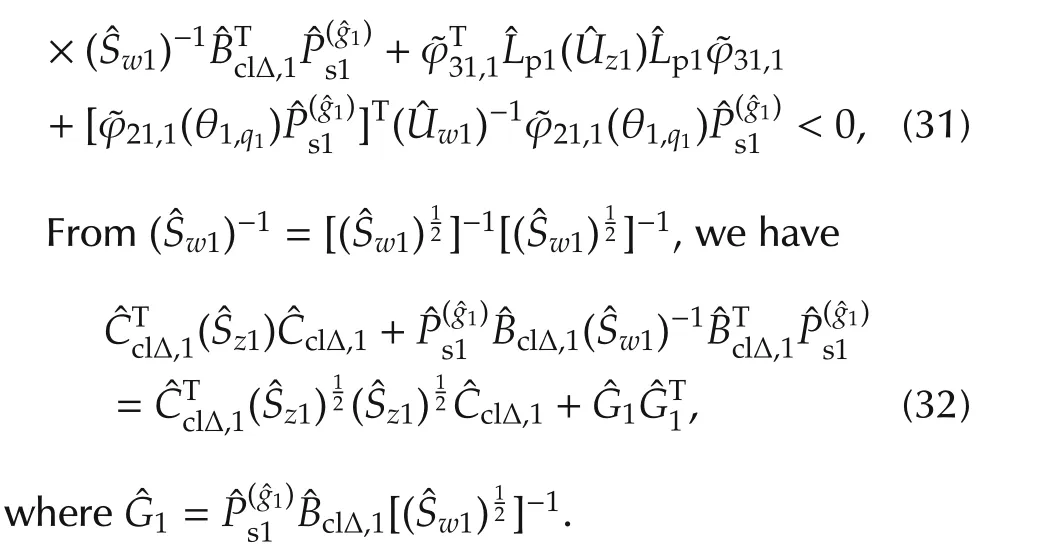
Substitution of(17)into(32)leads to

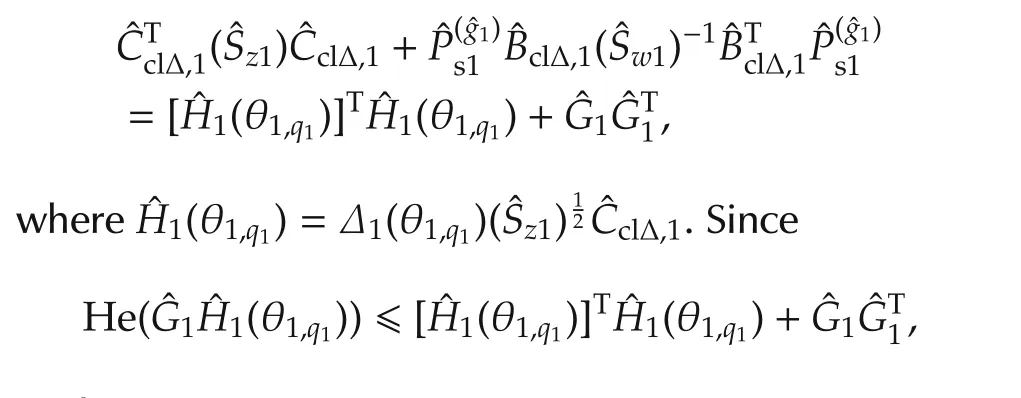
we have

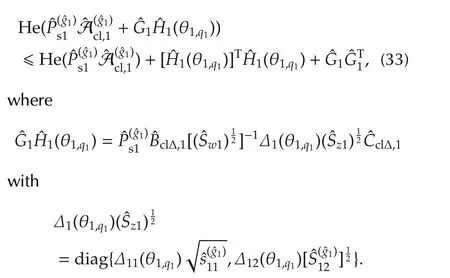
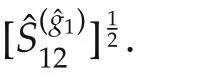
Therefore,we infer that

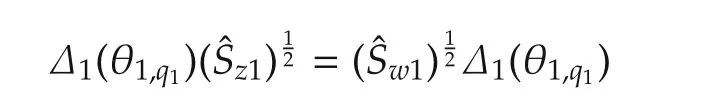
which leads to

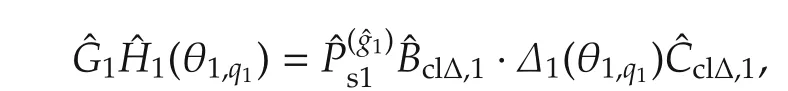
such that

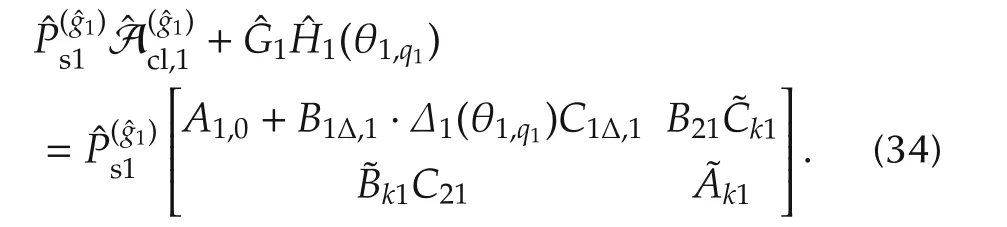
Substitution of(16)into(34)leads to

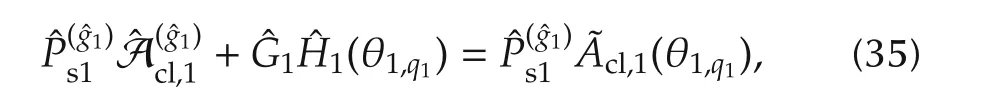
such that

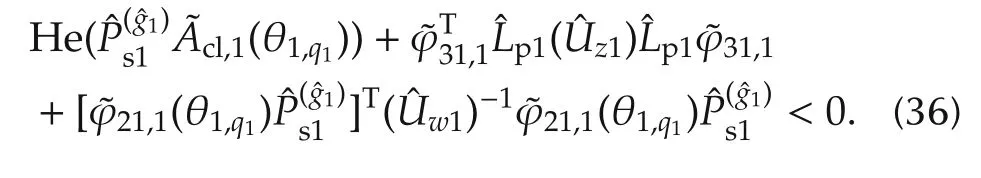
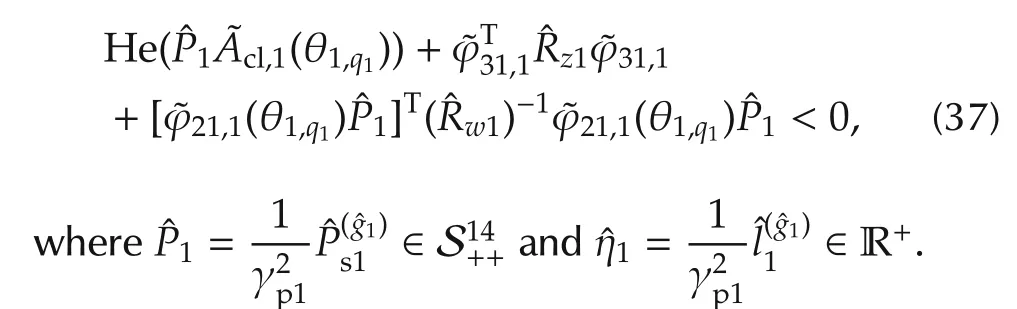
It is straightforward to show(29)holds for allq1. □

Suppose that for allq1,there exists γ1∈ R+,l1∈ R+andP1∈S14++such that

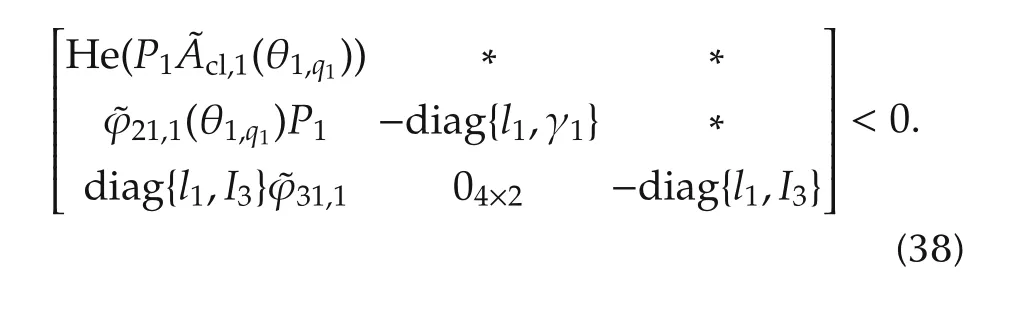
The LMI optimization problem to be solved is

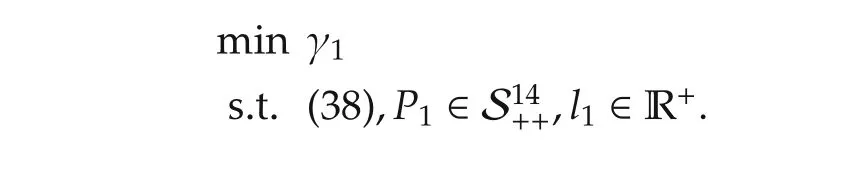
The set of optimal solutions is denoted by

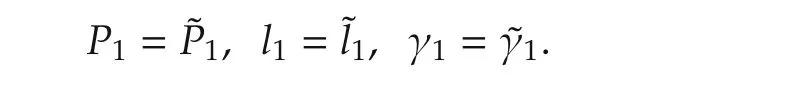
Corollary 1By Schur complement,we have

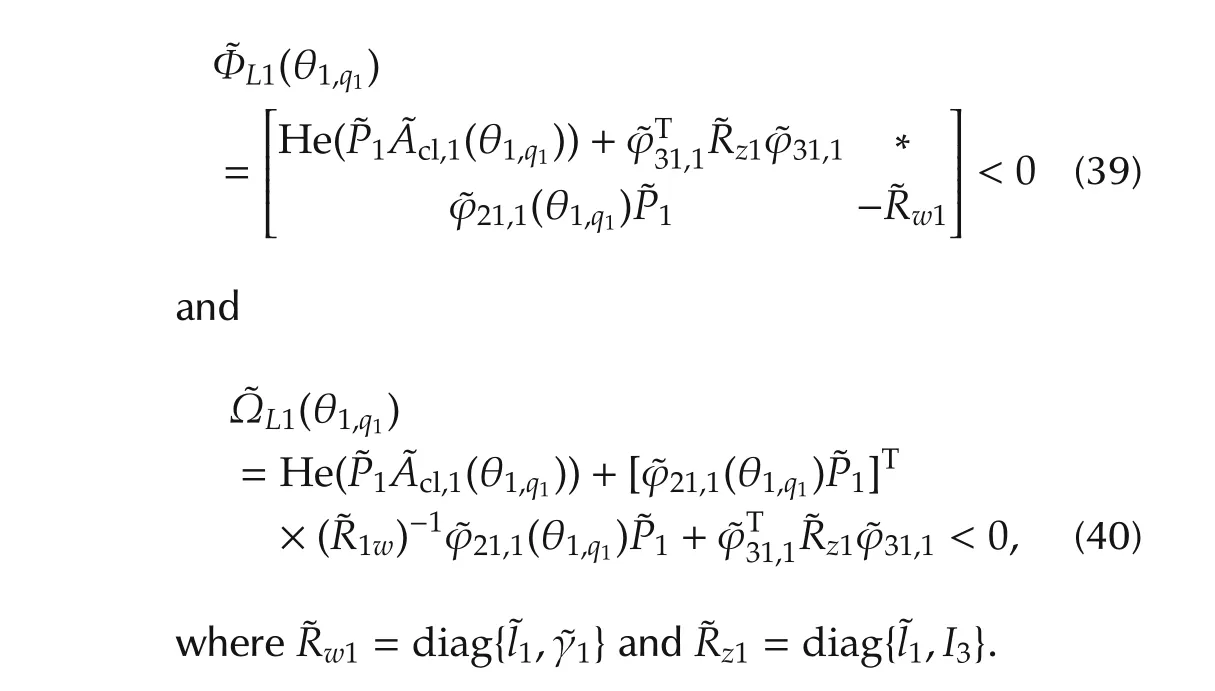
4.2 Controller synthesis for the second machine

The synthesized controller is expressed as

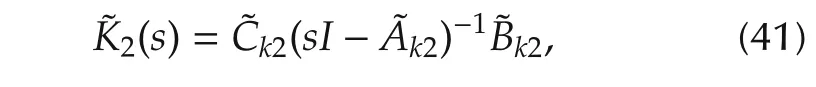
Corollary 2Inequality(42)is equivalently to

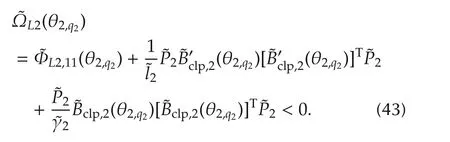
5 Performance evaluation

We can obtain the closed-loop interconnected system illustrated in Fig.3,by combining the decentralized controller

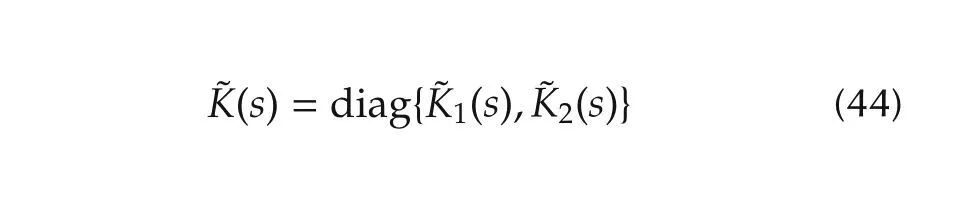
with the open-loop system given by(11)and(19).

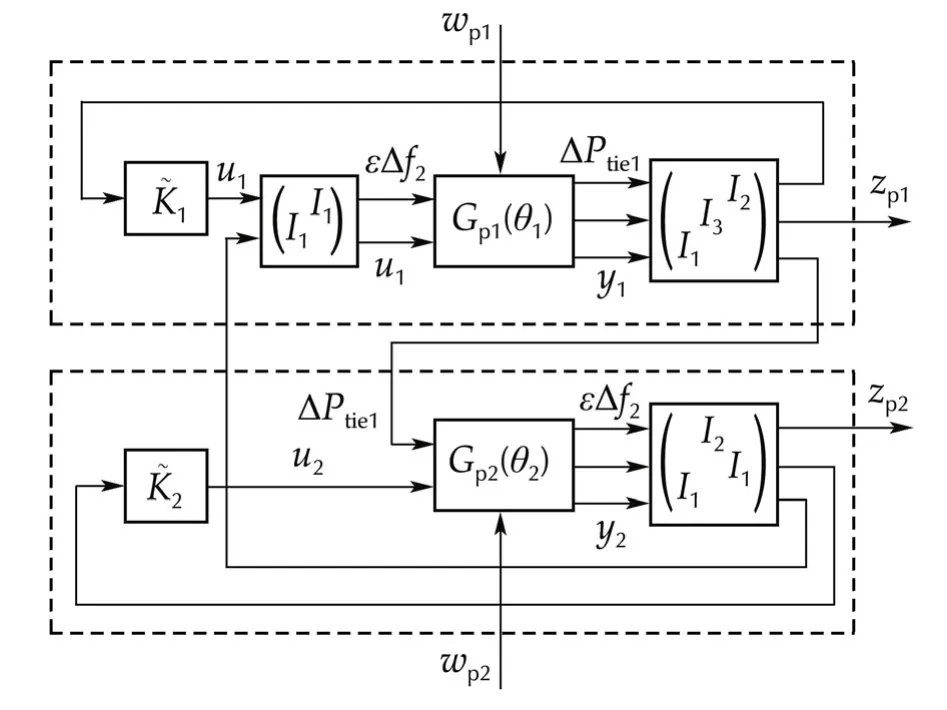
Fig.3 Closed-loop interconnected system.

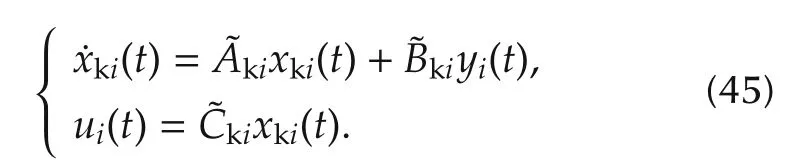
As shown in Fig.4,the whole closed-loop system is equivalently expressed as the interconnection of two closed-loop systems.

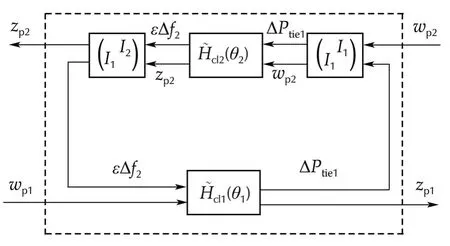
Fig.4 Equivalent closed-loop interconnected system.

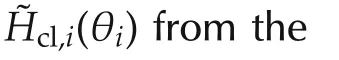
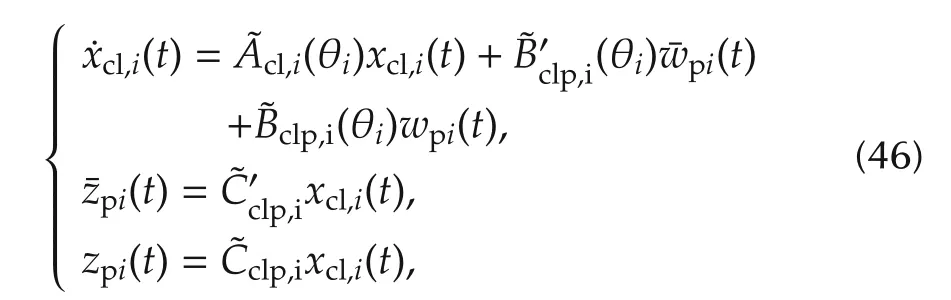
wherexcl,i(t)=col(xi(t),xki(t)).

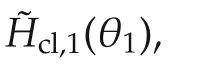
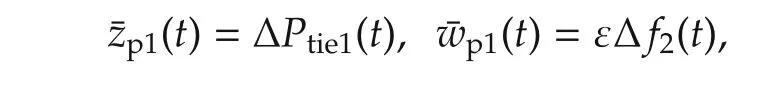
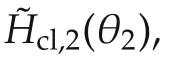
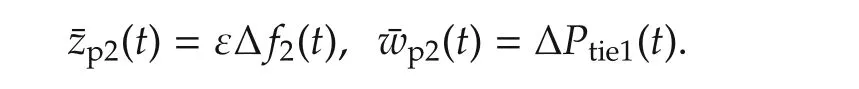
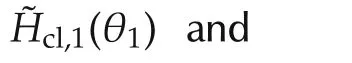
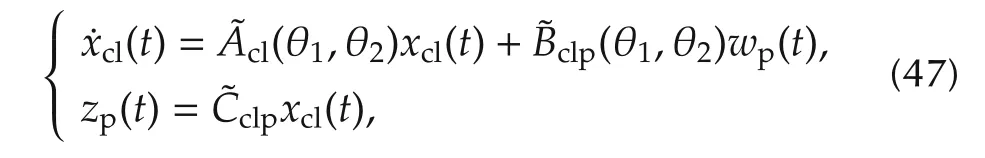
wherexcl(t)=col(xcl,1(t),xcl,2(t))∈R24and

Theorem 2The developed decentralized output feedback controller can make the closed-loop interconnected system

1)internally stable in the absence of disturbances;and

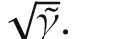
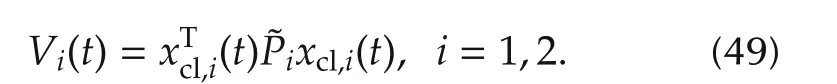
Differentiating(49)along the trajectories of(46)yields

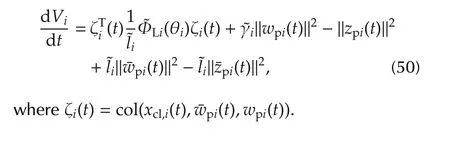
By means of the relationship

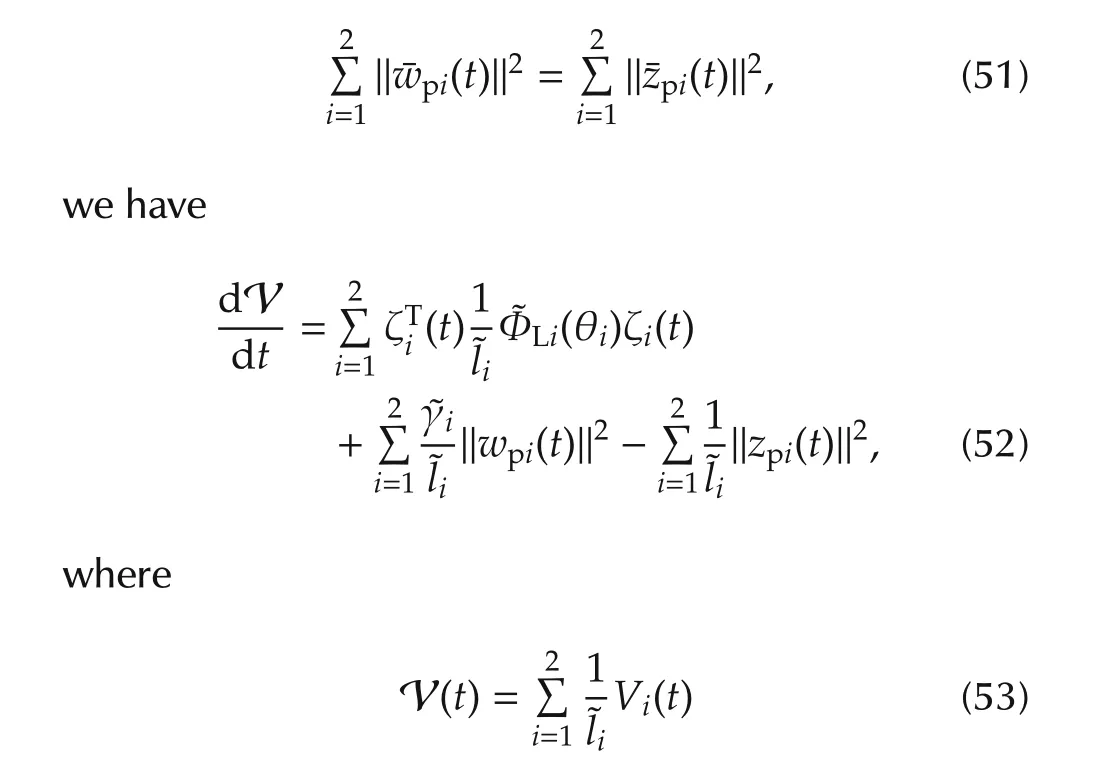
is a continuously differentiable,positive definite and radially unbounded function.

In view of(39)and(42),it is clear that for all θi∈ Θi,

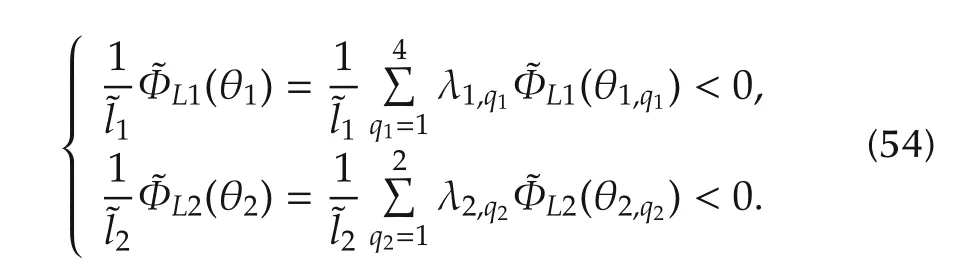
Case 1Supposewpis identically zero.

In this case,we deduce from(52)that

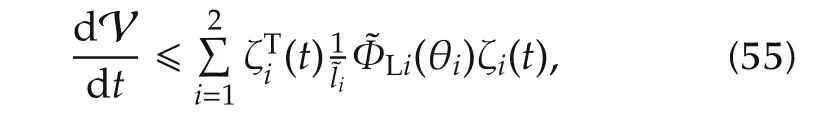
where ζi(t)=col(xcl,i(t),¯wpi(t),0).

Remark 7ζi(t)=0 ifxcl(t)=0.

Based on Lyapunov stability theorem,there is no difficulty to prove that(a)holds.

Case 2Supposewpis not identically zero.

From(52),we can deduce that

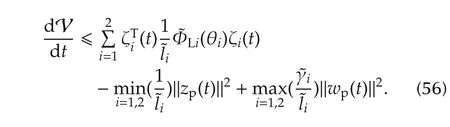
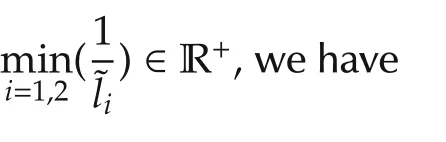
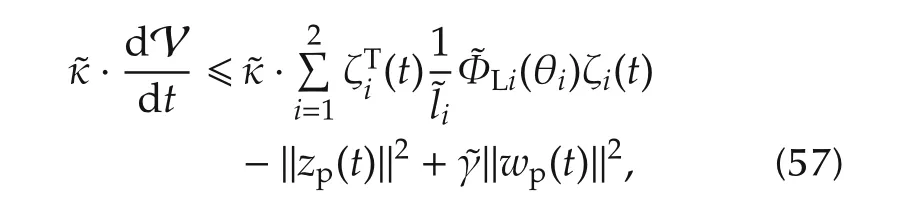
where

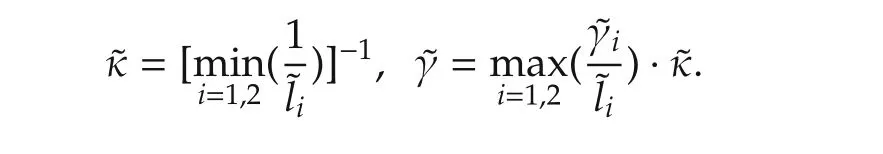
For the closed-loop interconnected system,we construct a Lyapunov function candidate of the form

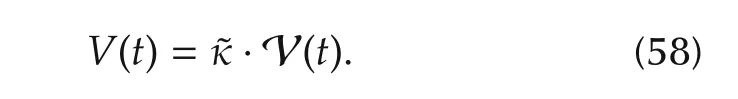
Suppose thatxcl(0)=0 such thatV(0)=0.

Integration of(57)on the interval[0,T]yields

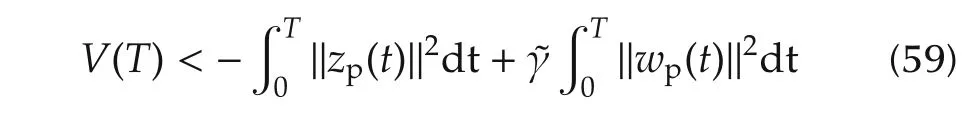
for allT＞0.

SinceV(T)≥0,and taking the limitT→∞,we have

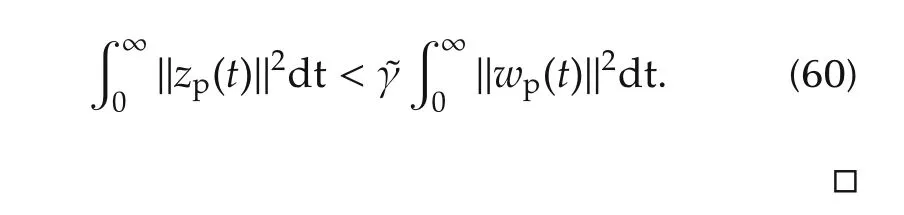
We will give another proof of Theorem 2 as follows.

ProofIn view of(40)and(43),it follows that

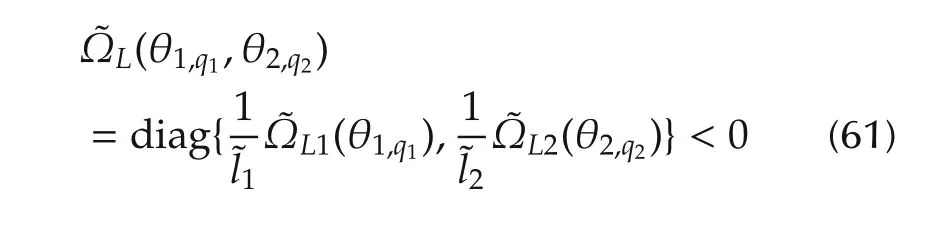
holds for allq1=1,...,4 andq2=1,2.

By matrix factorization,(61)can be rewritten as

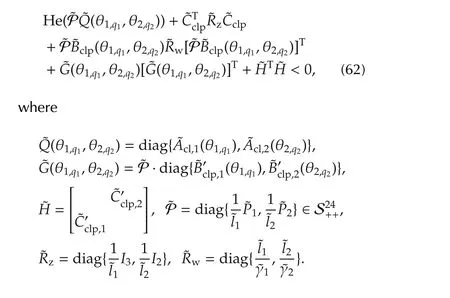
From the inequality

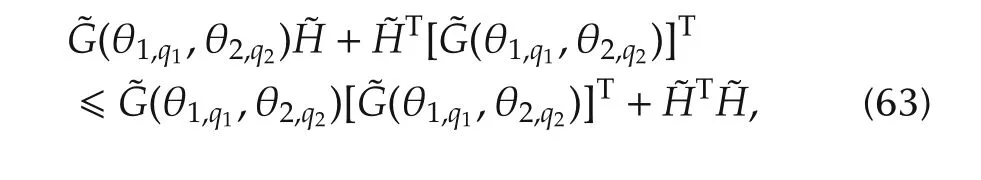
we have

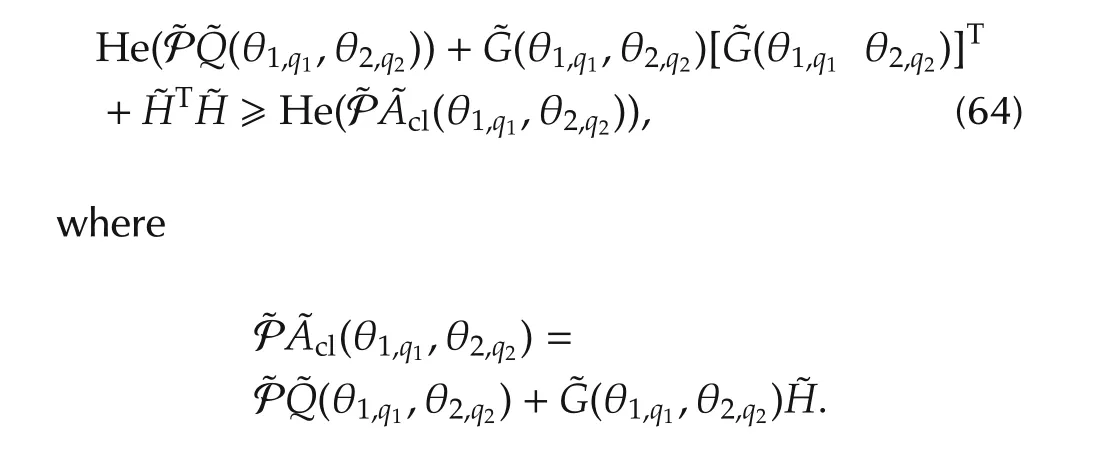
Based on above discussions,it follows that

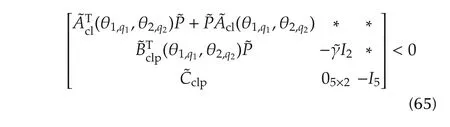
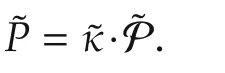
In view of bounded real lemma,it is clear that Theorem 2 holds. □

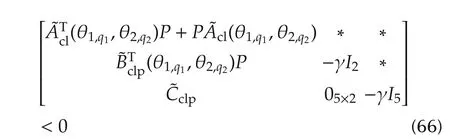
for allq1=1,...,4 andq2=1,2.

The LMI optimization problem to be solved is

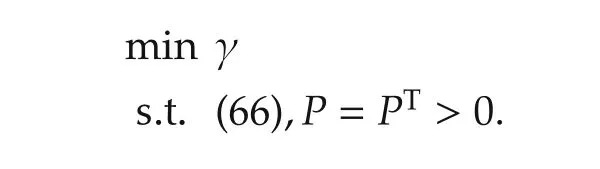
The set of optimal solutions is denoted by

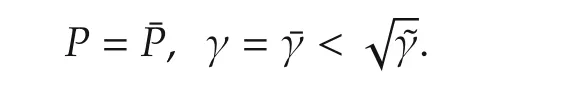
Based on bounded real lemma,we can confirm that

1)in the absence of disturbances,the closed-loop interconnected system is internally stable;and

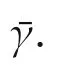
6 Simulation results

The system parameters are listed in Tables 1 and 2.

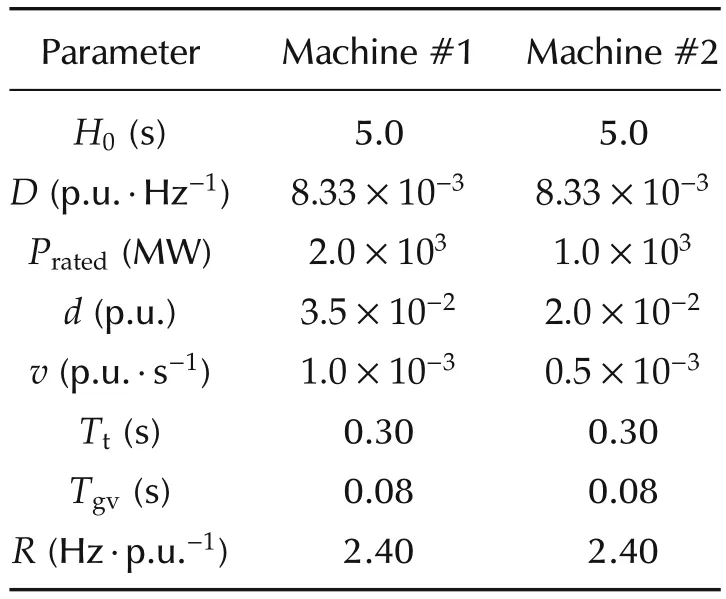
Table 1 Machine parameters.

Table 2 Tie line parameters.

The nominal operating points are

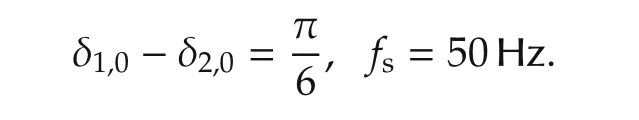
To evaluate the effectiveness of the proposed decentralized control scheme,simulations are carried out under different conditions.

Case 1The uncertain parameters are modeled as

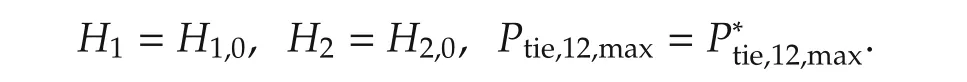
The simulation results are shown in Figs.5 and 6.

Case 2The uncertain parameters are modeled as

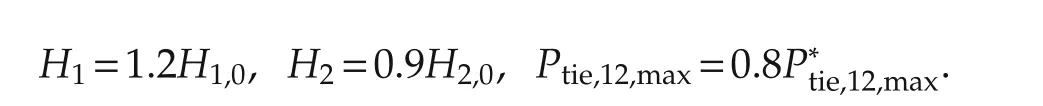
The simulation results are shown in Figs.7 and 8.

Case 3The uncertain parameters are modeled as

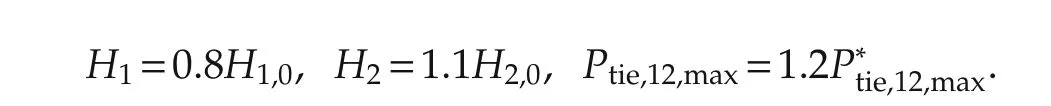
The simulation results are shown in Figs.9 and 10.

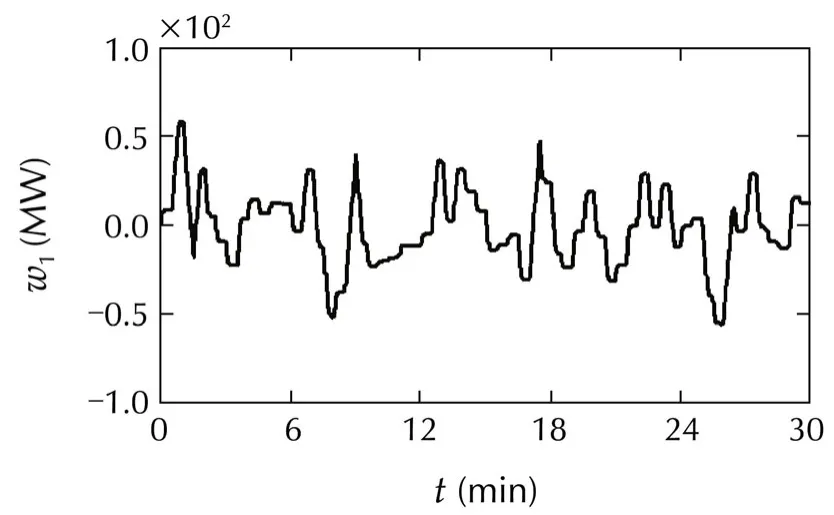
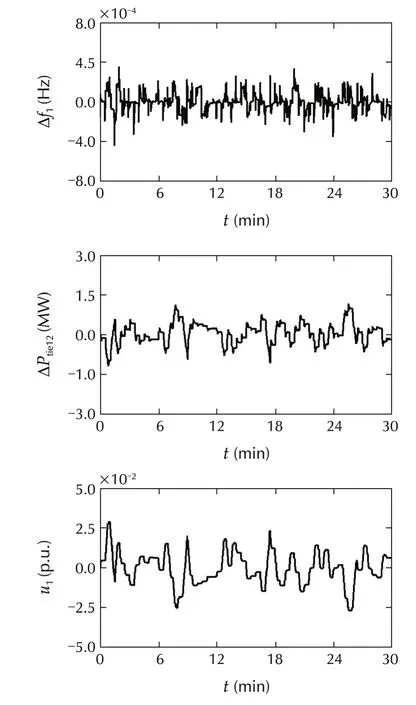
Fig.5 Responses of the first machine:Case 1.

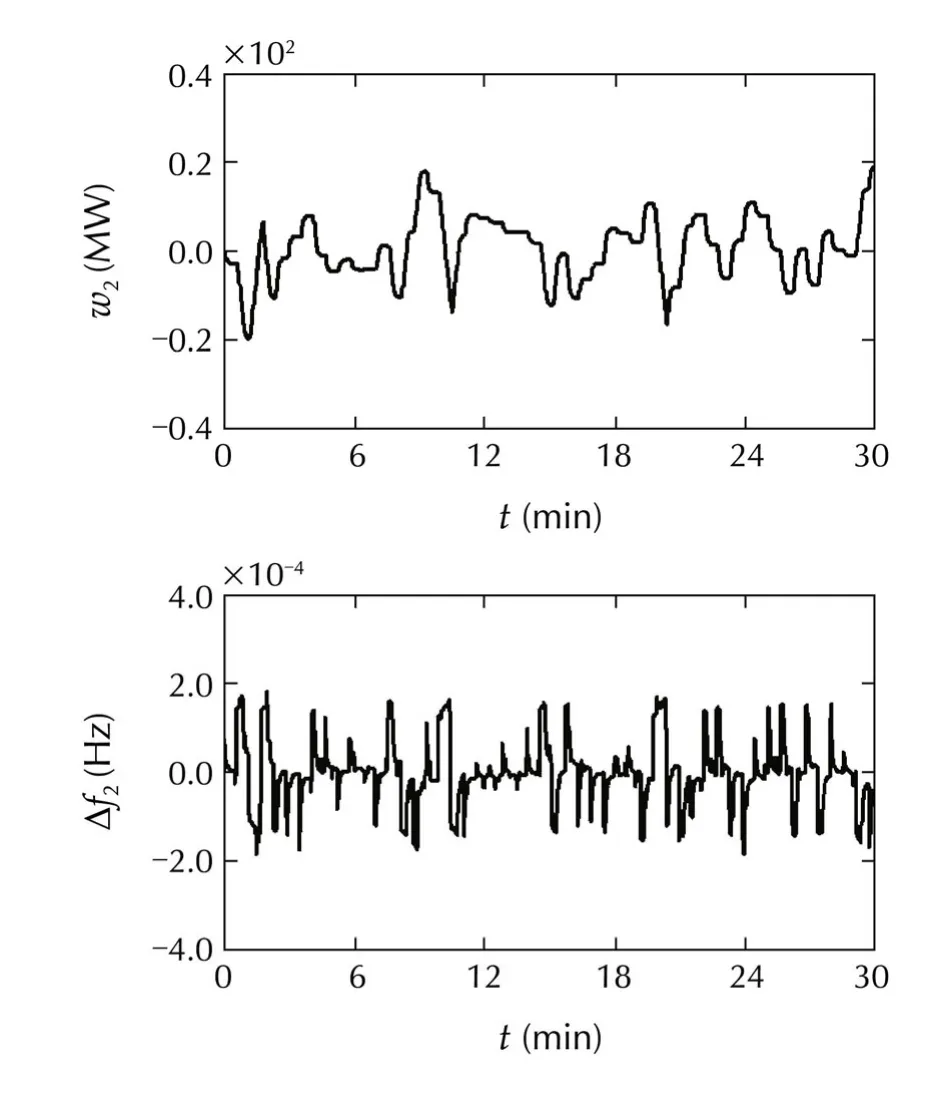
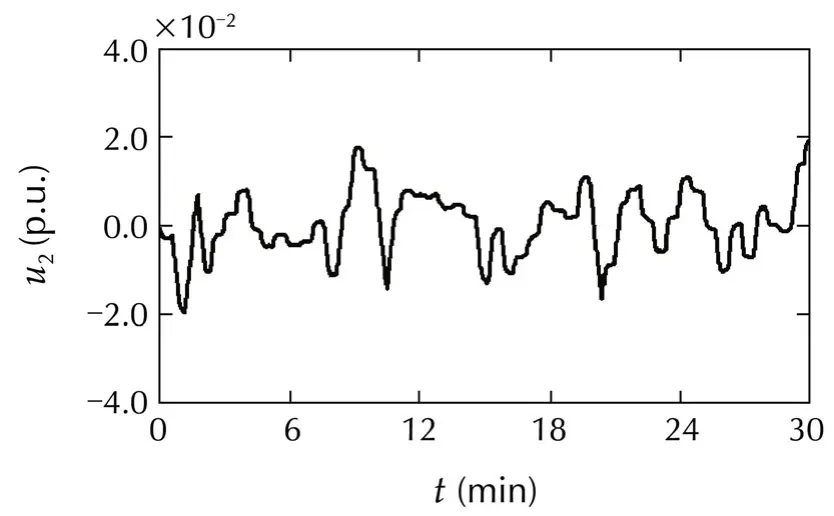
Fig.6 Responses of the second machine:Case 1.

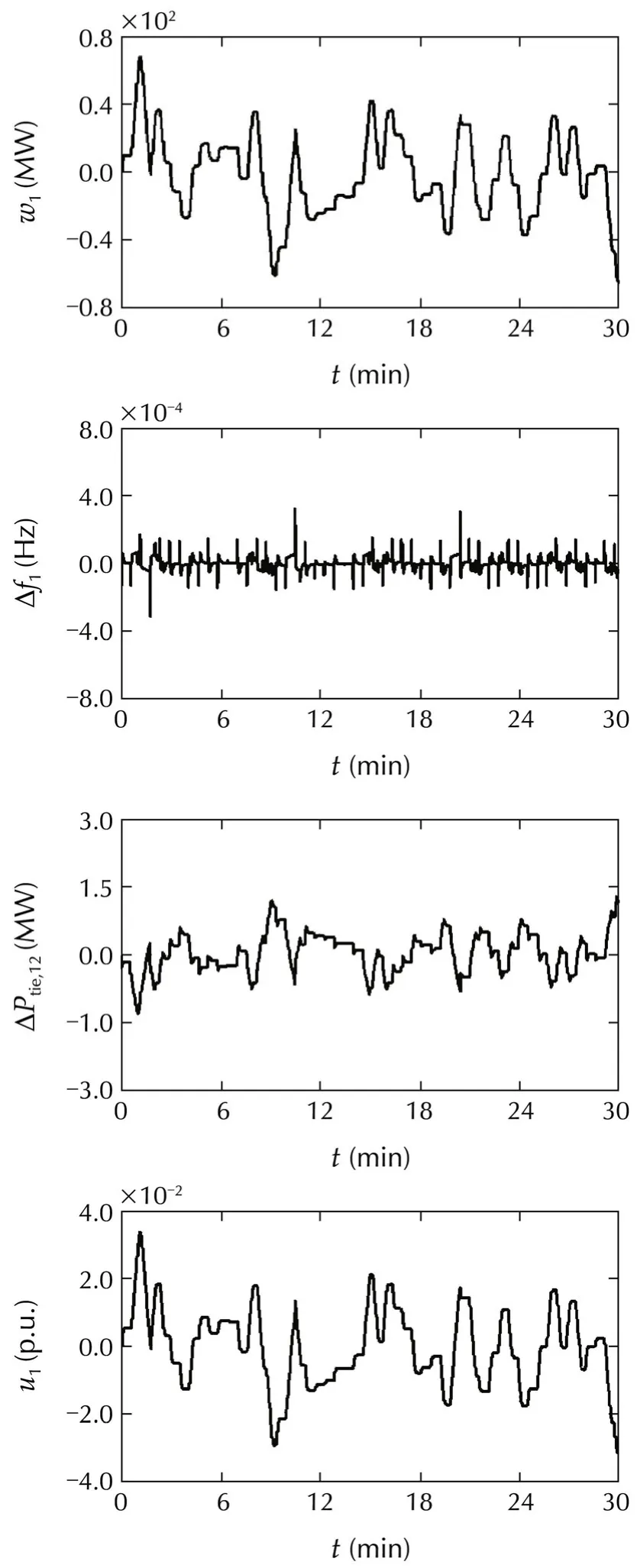
Fig.7 Responses of the first machine:Case 2.

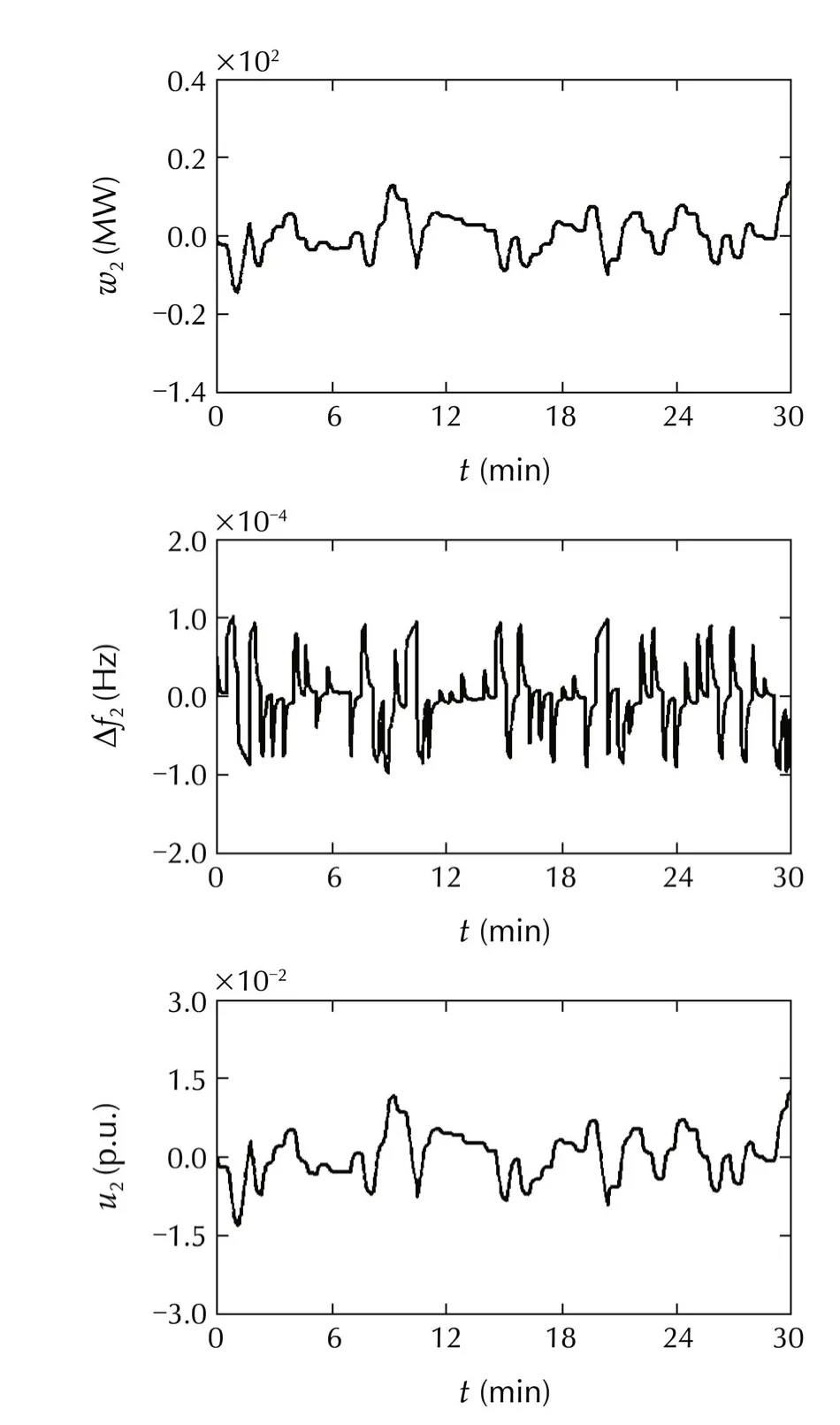
Fig.8 Responses of the second machine:Case 2.

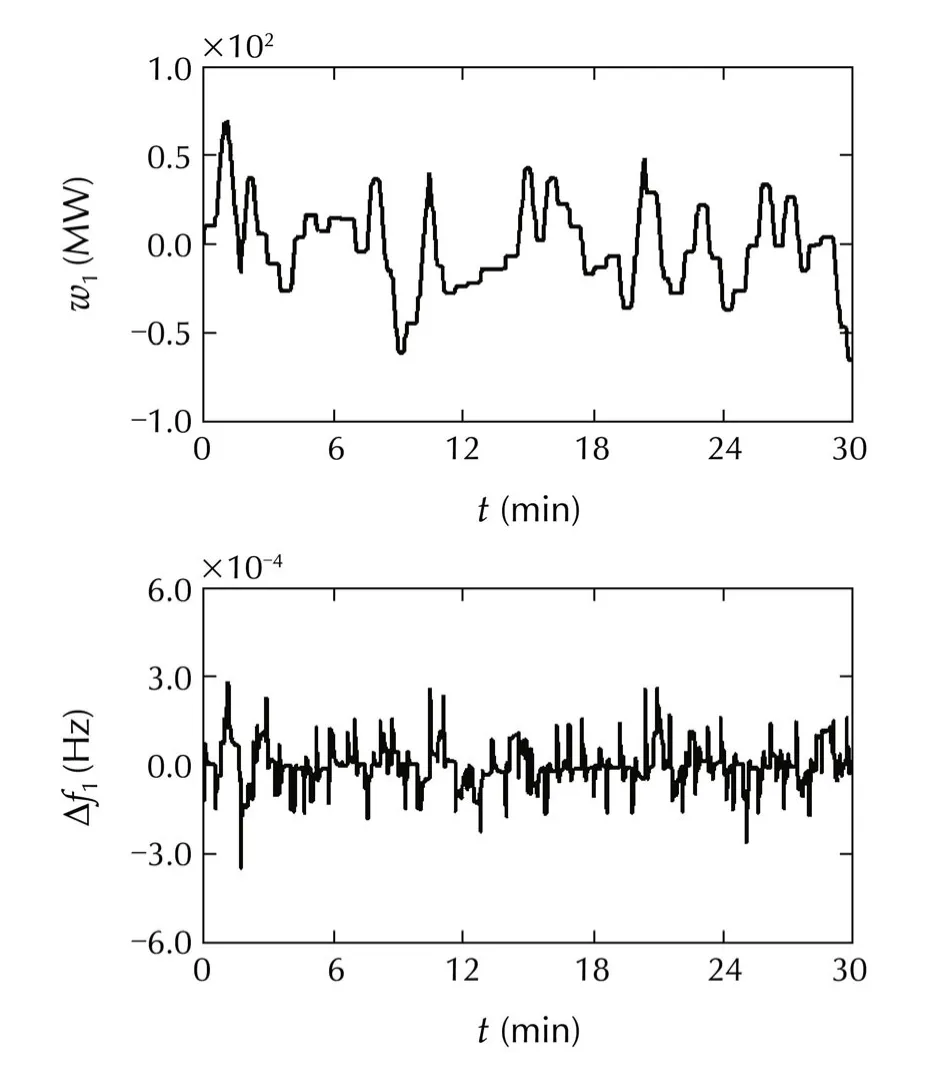
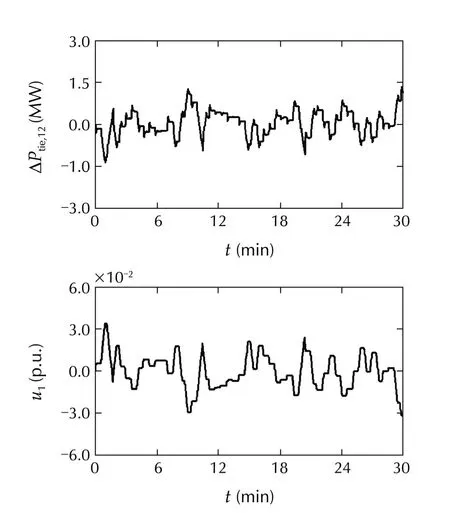
Fig.9 Responses of the first machine:Case 3.

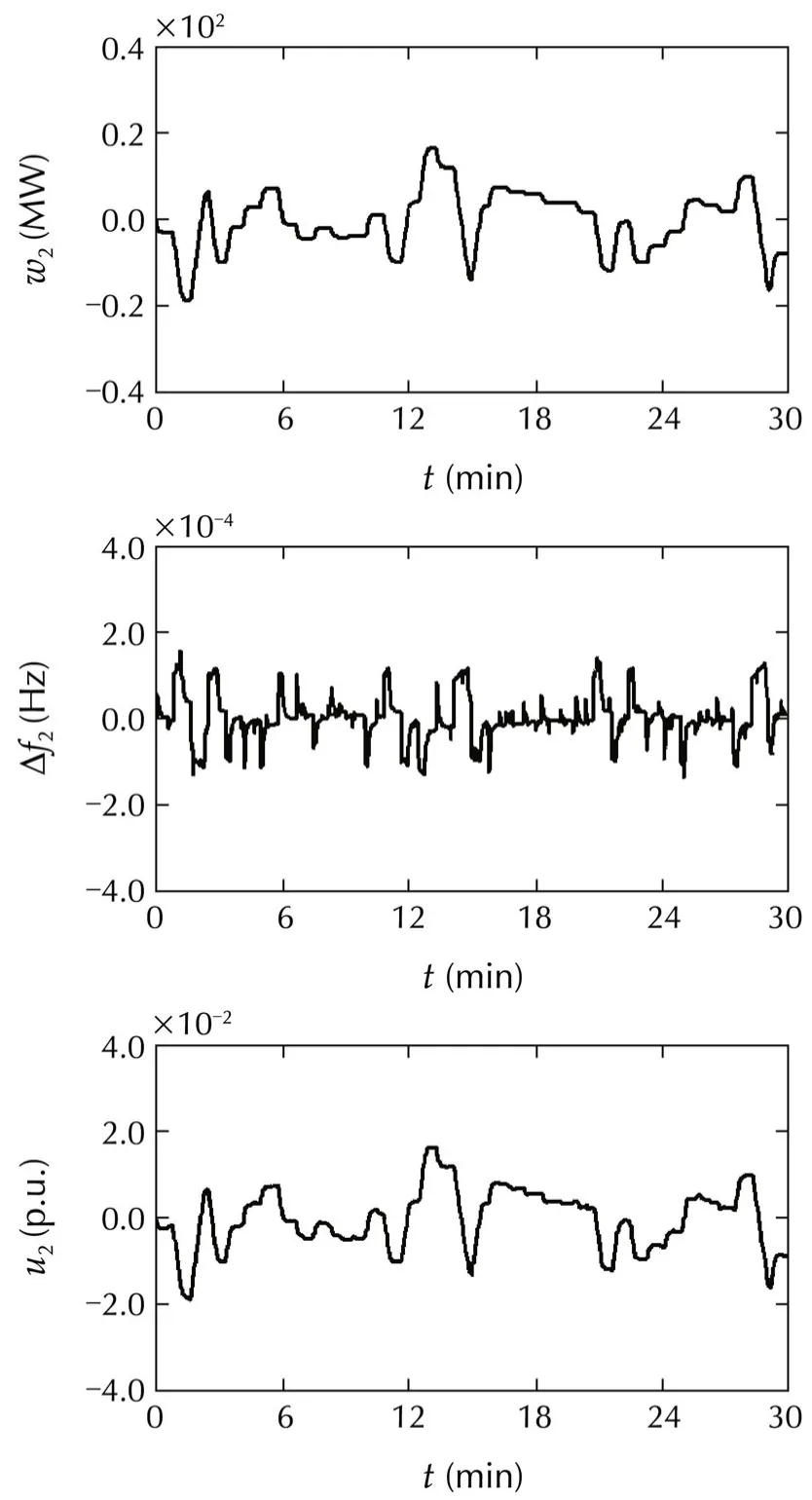
Fig.10 Responses of the second machine:Case 3.

In simulations,w1is modeled as a rapidly changing signal,whilew2is modeled as a slowly changing signal.

For convenience of analysis,load and tie line power deviations are expressed in terms of their actual values.

From the simulation results,we can confirm that

1)the frequencies are almost not influenced by irregular load variations and have been maintained close tofs;and

2)the tie line power deviations stay within their acceptable ranges.

7 Conclusions

In this paper,a decentralized control approach is proposed for a two-area interconnected power system.We formulate the controller synthesis problem as a scaled H∞control problem and propose an LMI-based algorithm to compute the decentralized controller.The synthesized controller enhances the system robustness to parameter uncertainties and attenuates bounded exogenous disturbances in the sense ofL2-gain.Simulation results exhibit a satisfactory performance.As the next step,we will develop the decentralized output feedback control scheme for large-scale power system.

[1]T.Suehiro,T.Namerikawa.Decentralized controlofsmartgrid by using overlapping information.Annual Conference of the Societyof-Instrument-and-Control-Engineers(SICE),Tokyo:Society of Instrument and Control Engineers,2012:125–130.

[2]N.Chen,M.Ikeda,W.Gui.Design of robust H∞control for interconnected systems:a homotopy method.InternationalJournal of Control,Automation,and Systems,2005,3(2):143–151.

[3]P.Kundur.Power System Stability and Control.New York:McGraw-Hill,1994.

[4]M.Miyazaki,K.Liu,O.Saito.Robust decentralized control approach to the multi area frequency control problem of power systems.Transactions of the Institute of Electrical Engineers of Japan–Part C,2002,121(5):953–960.

[5]F.Bianchi,H.De Battista,R.Mantz.Wind Turbine Control Systems:Principles,Modeling and Gain Scheduling Design.London:Springer,2006.

the B.Sc.degree in automatic control from North China Electric Power University,China in 2008,and the M.Sc.degree in Electrical and Electronic Engineering from Chiba University,Japan in 2013.He is currently studying at the Graduate School of Keio University as a Ph.D.candidate.His research interests are decentralized control,robust control,nonlinear control and their applications in power system.E-mail:claudioceke@163.com.

Hiromitsu OHMORIreceived the Bachelor’s Degree of Electrical Engineering,Master’s Degree of Electrical Engineering and Ph.D.from Keio University,Japan in 1983,1985 and 1988,respectively.From April 1988,he was the instructor of Department of Electrical Engineering,Keio University,Japan.From April 1991,he was an assistant professor of the same department.From April 1996,he was a associate professor of Department of System Design Engineering,Keio University.Currently,he is working as Professor at the same department.His research interests are in the field of adaptive control,robust control,nonlinear control and their applications.He is member of IEEE,SICE,ISCIE,IEE,IEICE,and EICA,etc.E-mail:ohm@sd.keio.ac.jp.

†Corresponding author.

E-mail:claudioceke@163.com.

©2015 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg