Circle formation control for multi-agent systems with a leader

2015-12-05LianjieZHAODanMA

Control Theory and Technology 2015年1期

Lianjie ZHAO ,Dan MA †

1.College of Information Science and Engineering,Northeastern University,Shenyang Liaoning 110819,China

2.State Key Laboratory of Synthetical Automation for Process Industries,Northeastern University,Shenyang Liaoning 110819,China

Received 29 June 2014;revision 28 January 2015;accepted 28 January 2015

Circle formation control for multi-agent systems with a leader

Lianjie ZHAO1,2,Dan MA1,2†

1.College of Information Science and Engineering,Northeastern University,Shenyang Liaoning 110819,China

2.State Key Laboratory of Synthetical Automation for Process Industries,Northeastern University,Shenyang Liaoning 110819,China

Received 29 June 2014;revision 28 January 2015;accepted 28 January 2015

In this paper,we focus on circle formation control of multi-agent systems(MAS)with a leader.The circle formation is achieved based on the lead-following and the artificial potential field method.A distributed control law is given to make a group of agents form a circle and consequently achieve an expected angle.Finally,simulation results show that the proposed circle formation strategies are effective.

Circle formation,artificial potential field method,multi-agent systems,distributed control

DOI 10.1007/s11768-015-4092-8

1 Introduction

A multi-agent system is an important system of complex systems,and also a branch of distributed artificial intelligence.The cooperative control of multi-agent systems has got considerable attention[1–10].As a class of problem of cooperative control for multi-agent systems,the formation behavior can be widely found in engineering,biology,robots and entertainment,etc.Especially in military,formation control has been used in spacecrafts,such as the unmanned aerial vehicle(UAV)formation,and the autonomous underwater vehicle(AUV)navigation.

As we all know,there exist lots of formation behavior in the nature,such as birds,fishes,insects,etc.They always form a pattern for the purpose of hunting for food and defending enemy.Through the formation behaviors,they can easily search and hunt,and also reduce the possibility of suffering attack.There are lots of methods to dealwith the formation controlofMAS,such as artificial potential field method[11],leader-following method[12–15],based on behavior[16],based on virtual method[17].However,there still exist lots of problems to be solved on formation control.

As for the pattern formation problem,one usually requires the agents to form a specific pattern,such as linear,triangular,rectangular,and circular.In the study of linear formation,leader-follower method was usually used to achieve the specific pattern under a distributed control law[18].For the triangle formation control,reference[19]analyzed various of distributed control laws and then presented a new control to show that the proposed control law can cause any initially non-collinear,positively-oriented,three agent formation to converge exponentially fast to a desired positively-oriented triangular formation.Reference[20]gave a method based on V function of adjacency information,and achieved the triangle formation for a group of agents.

There are some literatures to study the circle formation control problem.Reference[21]gives a definition of circle formation,and presents a distributed control law for a group of agents that move and only move on a given circle.In[22],the cooperative control of targetcapturing task based on a cyclic pursuit strategy is studied,but the premise is all the agent are distributed on a circle in the initial moments.Reference[23]also studies the circle formation problem,but it does not take the communication range of the agents into account.Reference[24]proposes a simple algorithm to solve the circle formation problem.A control law under some assumption that all the agents move only on a circle is studied in[25].Reference[26]have studied a control law under which the multi-vehicle system’s equilibrium formations are generalized circular pursuit patterns.

In this paper,we study the circle formation control of multi-agent systems with a leader.First,we present an artificial potential function for the follower agents and the leader agent based on the leader-following and the artificial potential field method,consequently achieve the goal that all the agents move to a virtual circle.Second,we propose a distributed control law for the group of agents using the potential function method.Once forming the circle,the follower agents can only use the position information of the adjacent agents and the leader agent.Finally,each follower agent achieves the expected angle.

The rest of the paper is organized as follows.In Section 2,we give a definition of circle formation problem.Then we propose a method to force the agents to form a circle in Section 3.A distributed control law for a group of agents are proposed in Section 4.In Section 5,simulation examples are given to verify the correctness and effectiveness of the method.

2 Problem formulation

We considerNfolloweragents(N1)and one leader agent.Suppose that all the agents distribute clutter in the 2D space,and the leader agent is the center of an expected circle.We also assume that there is no collision among the follower agents.The objective is that theNcooperative agents can form a circle with radiusr;and reach an expected angle ϕij.As it is shown in Fig.1,p0presents the position of the leader agent,pi,i=1,2,...,Ndenote the position of the follower agents.ris the expected distant between the leader agent and each follower agent.ϕijis the expected angle between the follower agent and its neighbor,a desired circle formation is admissible

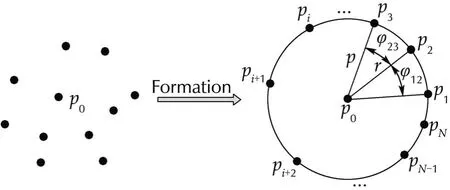
Fig.1 The process of forming a circle.

For simplicity of analysis,we mark the number for each agent once if the circle is forming.Assume that each follower agent can obtain the positions of the leader.We use a graph to describe the relationships among the agents.For a graphG=(v,ε),where is the vertex setv={0,1,2,...,N},which denotes a set includingN+1 nodes and the directed edge set ε={(0,1),...,(0,N),(1,2),(2,3),...,(1,N−1),(N,1)},where ε denotes the adjacency relationship between the nodes.

Denote theith follower agent’s neighbor byj,then we know that

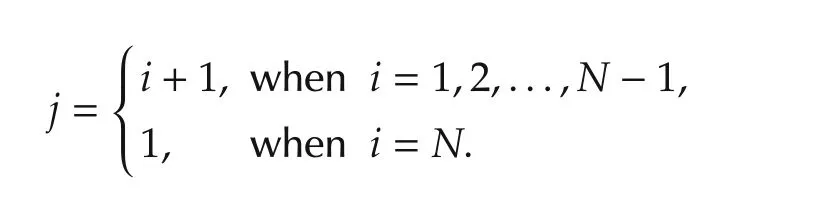
Each follower agent is described by the following firstorder dynamic system:

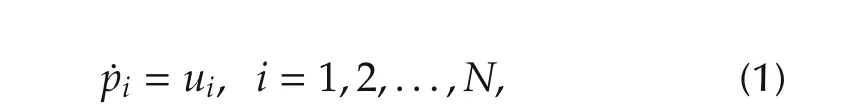
wherepidenotes the position information of the followeragenti.uidenotesthe controlinputofthe follower agent.

The leader agent is described as follows:

Def i nition 1(Circle formation problem) Given an expected radiusr,determine a leader as the center of a circle.Design a potential function to make the distance between each follower agent and leader agent satisfyingpi−p02=r.Then,design distributed control lawui,i=1,2,...,Nfor the follower agents on the formed circle above,and let the angle between the follower agentiand its neighborjreach the expected angles ϕij,which satisfies withMoreover,in the process of reaching expected angle the circle formation is keeping all the time.

Remark 1Different from[21],in which consider a group of agents that move and only move on a given circle,we consider the case that all the agents distribute clutter in a 2D space which are not on a given circle.We need to present control laws for a group of agents combining the potentialfunction method to form a circle and reach the expected angle.

3 Forming circle based on potential function

In this section,we present a control law for theNfollower agents to reach a circle with the centerp0and the expected radiusr.

In what follows,we will find a potential functionVi0forthe leaderagentand the followeragentsbased on the artificial potential field method.EachVi0is used to control the distanceri0between the leader agent and each follower agent,whereri0=pi−p02is a non-negative,differentiable function.Finally,a circle is formed when the relative distanceri0,i=1,...,Nis equal to the expected radiusr.

Theorem 1Multi-agent system(1)with a leader(2)under the distributed control law

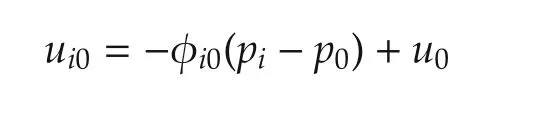
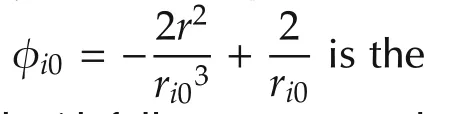
ProofDefine a potential function for the leader agent and the follower agents as follows:

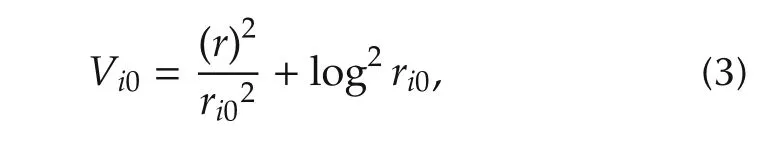
whereris the expected radius,ri0,i=1,...,Nis the distances between the leader agent and each follower agent.

From(3),we can obtain the pulling force function for the leader agent and each follower agent:

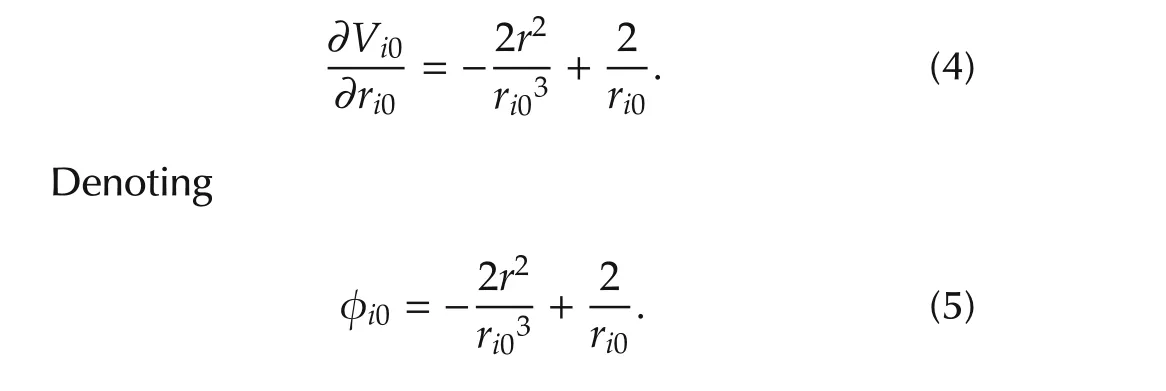
Then we choose the control law for forming the circle as follows,i.e.,

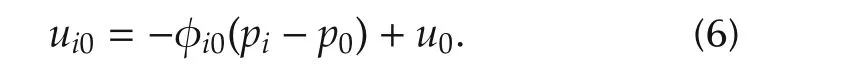
Now,let us analyze how the control law helps the agents form the circle with the expected radiusrand the centerp0,ifri0=r,we know that φi0=0,then the force between the leader agent and the follower agent is zero(keeping the expected distance).Ifri0gt;r,we know thatφi0gt;0,then the force between the leaderagentand the follower agents is greater than zero(pulling back to the expected distance).Ifri0lt;r,φi0lt;0,then the force between the leader agent and the follower agents is less than zero(rejecting to the expected distance).

前言:近年来，我国企业的发展规模随着市场的变化而改变，人力资源管理属于企业发展中的重要环节。为了实现可持续发展，企业必须选择与自身发展相协调的管理模式。人力资源管理虽然能为企业的发展提供动力，但管理不善将会影响企业的运营。笔者依据当今社会时代的发展，探讨了人力资源管理模式及其选择因素，希望提供给企业一定的参考意义。

Remark 2The artificial potential field method is a virtual force method proposed by Khatib[11].It was first used in the obstacle avoidance and path planning of multi mobile robots.The basic idea is that one can design a field of force(including target and obstacle)as the surrounding environment and the mobile robots move in the field.In the field,the force between the target and robots is gravitation and the force between the obstacle and robots is repulsion.In this paper,we use this method to adjust the distance between the follower agents and the leader agent.

4 Distributed control law design

Combining the above forming circle process,we focus on designing distributed control laws for each follower agent to reach the expected angle ϕijbetween the follower agents in this section.Moreover,in the process of reaching expected angle ϕijthe radiusrof the circle will be maintained.

Assumption1ϕijisthe expected angle between the follower agent and its neighbor,and ϕijmin{σi,σj},where σiand σjis the communication radius(scope).

Remark3We draw a new circle with the center(theith follower agent),there are two intersections with the circle formed in Section 3.Then we call the arc between those two intersections is the communication scope.Moreover,the angle transformed by the arc is σi.

Assumption 2After forming the circle,theith follower agent’neighbor is located in the communication scope.

Theorem 2Multi-agent control system(1)and the leader(2).If under the distributed control law,

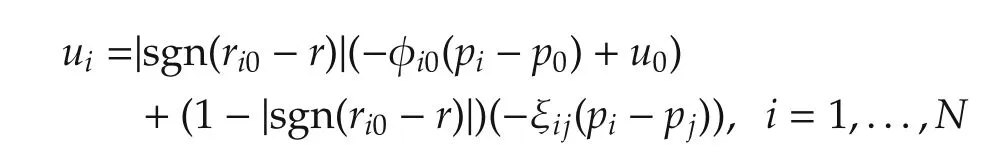
reaches the expected angle ϕijand remains the circle with radiusr,and then,the circle formation problem is solvable.where φi0is the pulling force function between theith follower agent and the leader agent,ϕijis the pulling force function between theith follower agent and its neighbor,andu0is the control input of the leader agent.

ProofDefine the potential function for follower agents located on the circle,which is formed in the above section,

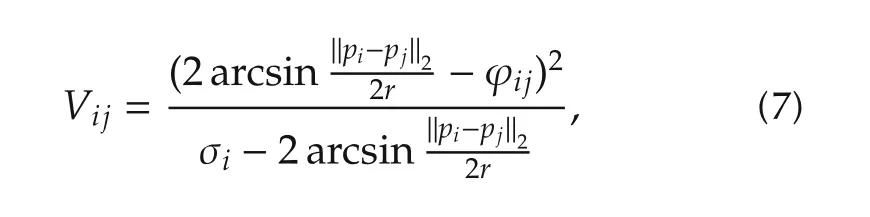
where σiis the communication radius(which can be described by the angle),ris the radius of the circle formed.In the above section,ϕijis the expected angle between any adjacent follower agents,and ϕijmin{σi,σj}.pi−p j2is the distance between the follower agentiand its neighborj.2 arcsinis the angle between the follower agentiand its neighborj.

Lettingrij=pi−p j2and αij=2 arcsinobtain the pulling force function for the follower agents:

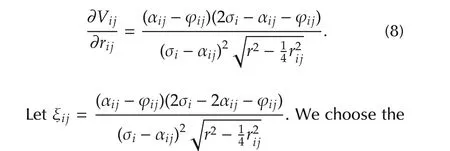
second part of control lawuifor the follower agents,which can force the agents to reach the expected angle ϕij,i.e.,

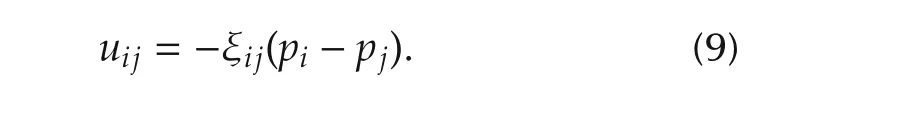
Then we obtain the distributed control lawuifor the follower agents:

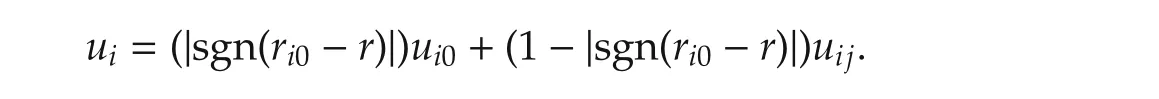
Moreover,the control lawuican be written as

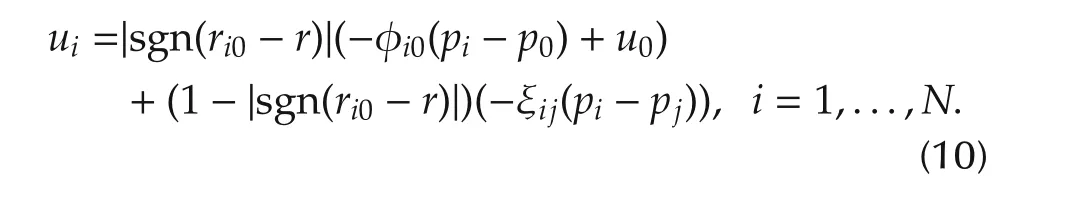
Defining the potential function as follows:

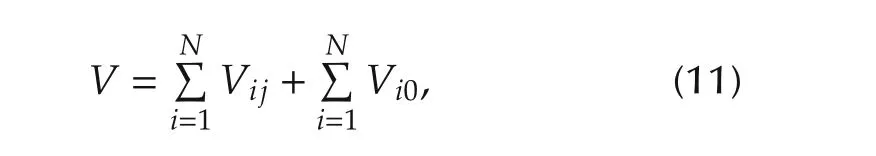
the derivative ofValong systems(1)and(2)is

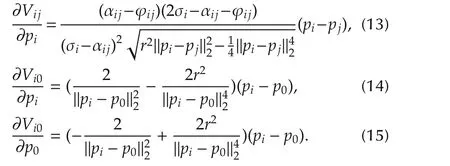
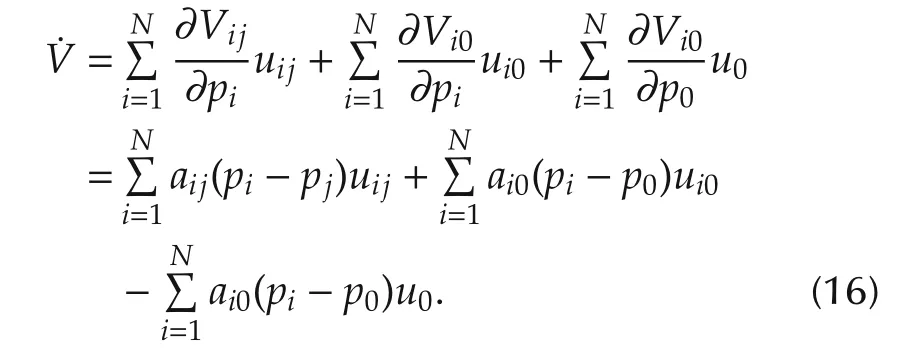
Substituting(10)into(16),withu0=0,we have

Sinceaijand ξij,ai0and φi0are positive or negative simultaneously,we can obtain

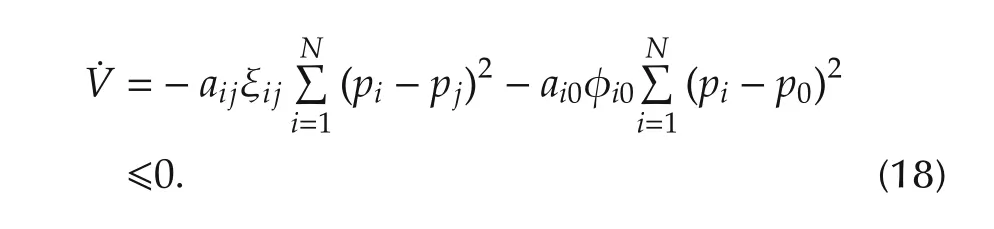
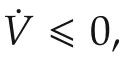
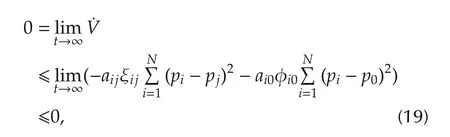
which implies that

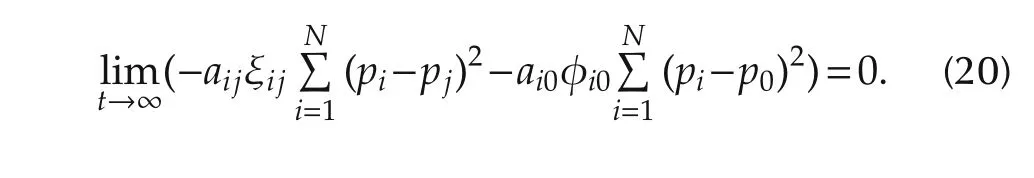
Remark 4In the control law(10),the first term is a force between the follower agentiand the leader agent,in which it is used to keep the distancerbetween the follower agent and the leader agent.The second term is a force between the follower agentiand its neighborj,in which it is used to drive the follower agent to reach the expected angle.In other words,ifri0−r=0,we have|sgn(ri0−r)|=0,then the second term works;ifri0−r?0,we have|sgn(ri0−r)|=1,then the first term works.

5 Examples

In this section,we give two examples to verify the results proposed in Theorems 1 and 2.

Example 1Consider a group of 5 agents(including a leader agent)trying to form a circle,the center of the circle is the leader agent,and the expected radius isr=5.Given the leader agent’s initial position is(5,5),the initial positions of the other four follower agents are(18,5),(5,16),(15,5),(5,8),respectively.The leader agent’s control input isu0=0,the follower agents’control law is satisfied with(10).

Fig.2 indicates the distance variation between the leaderagent(L-agent)and the followeragents(F-agents).We can find that the distances between each follower agentand the leaderagentcan reach the expected radiusr=5,forming and keeping the circle formation.

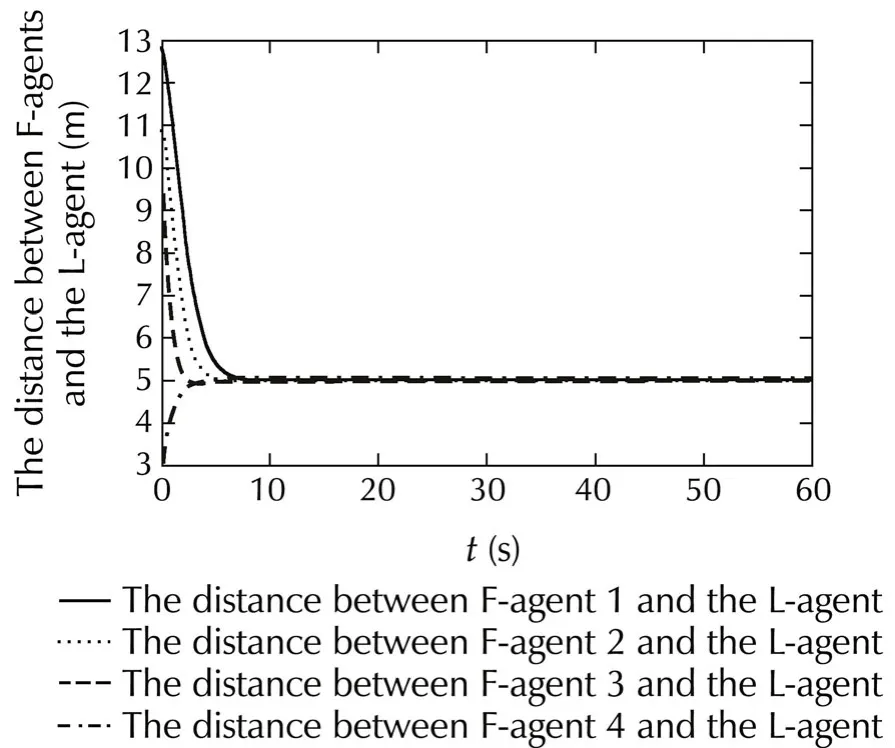
Fig.2 The distance between F-agents and the L-agent.

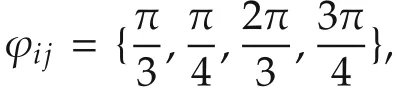
Fig.3 indicates that the distances between any adjacent two follower agents tend to the expected distance(angle),and also all the follower agents maintain the formed circle.

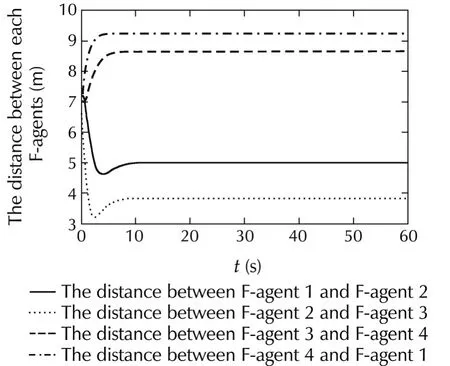
Fig.3 The distance between any two follower agents(reach the expected angle).

6 Conclusions

We have proposed distributed control laws for multiagent systems to achieve circle formation along with a given radius and any expected angle.Based on the potential function and the leader-following method,the proposed distributed control laws lead agents to form a circle.Moreover,we have presented anothercontrollaw to lead the follower agents which locate on the formed circle to reach the expected angle.Simulation results show that effectiveness of the proposed methods.

[1]C.Yan,W.Zhu.Consensus analysis of second-order multiagents systems with multiple time delays and Switching topologies.Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition,2011,23(4):478–482.

[2]R.Olfati-Saber,R.Murray.Consensus problems in networks of agents with switching topology and time-delays.IEEE Transactions on Automatic Control,2004,49(9):1520–1533.

[3]W.Zhu,D.Cheng.Leader-following consensus of second order agents with multiple time varying delays.Automatica,2010,46(12):1994–1999.

[4]Y.Hong,J.Hu,L.Gao.Tracking controlformulti-agentconsensus with an active leader and variable topology.Automatica,2006,42(7):1177–1182.

[5]Q.Hui,W.Haddad.Distributed nonlinear control algorithms for network consensus.Automatica,2008,44(9):2375–2381.

[6]P.K.C.Wang.Navigation strategies for multiple autonomous mobile robots moving in formation.Journal of Robotic Systems,1991,8(2):177–195.

[7]J.Fax,R.Murray.Information flow and cooperative control of vehicle formations.IEEE Transactions on Automatic Control,2004,49(9):1465–1476.

[8]S.Roy,A.Saberi,K.Herlugson.Formation and alignment of distributed sensing agents with double-integrator dynamics and actuator saturation.Sensor Network Applications.New York:Wiley-IEEE Press,2004:Section 3.4.

[9]H.Atrianfar,M.Haeri.Adaptive flocking control of nonlinear multi-agent systems with directed switching topologies and saturation constraints.Journal of the Franklin Institute,2013,350(6):1545–1561.

[10]H.M.La,R.S.Lim.Decentralized flocking control with a minority of informed agents.Proceedings of the 6th IEEE Conference on Industrial Electronics and Applications,Beijing:IEEE,2011:1851–1856.

[11]O.Khatib.Real-time obstacle avoidance for manipulators and mobile robots.Proceedings of IEEE International Conference on Robotics and Automation.Missouri:IEEE,1985:500–505.

[12]J.Desai,J.Ostrowski,V.Kumar.Controlling formations of multiple mobile robots.Proceedings of IEEE International Conference on Robotics and Automation,Leuven,Belgium:IEEE,1998:2864–2869.

[13]L.Consolini,F.Morbidib,D.Prattichizzob,et al.Leader-follower formation control of nonholonomic mobile robots with input constraints.Automatica,2008,44(5):1343–1349.

[14]E.S.Kazerooni,K.Khorasani.Semidecenttalised optimal control technique for a leader-follower team of unmanned systems with partial availability of the lead command.Proceedings of the IEEE International Conference on Control and Automation,Guangzhou:IEEE,2007:475–480.

[15]F.Chen,W.Ren.Surrounding control in cooperative agent networks.Systemsamp;Control Letters,2010,59(11):704–712.

[16]X.Mu,Y,Du,X.Liu,et al.Behavior-based Formation Control of Multi-Missiles.Chinese Control and Decision Conference,Guilin:IEEE,2009:5019–5023.

[17]M.Lewis,K.Tan.High precision formation control of mobile robots using virtual structures.Autonomous Robots,1997,4(4):387–403.

[18]S.Sandeep,B.Fidan,C.Yu.Decentralized cohesive motion control of multi-agent formations.Proceedings of the 14th Mediterranean Conference on Control and Automation,Alcona,Italy:IEEE,2006:944–949.

[19]M.Cao,A.Morse,C.Yu,et al.Maintaining a directed,triangular formation of mobile autonomous agents.Communications in Information and Systems,2011,11(1):1–16.

[20]H.Yu,P.Antsaklis.Formation controlofmulti-agentsystems with connectivity preservation by using both event-driven and timedriven communication.Proceedings of the 51st IEEE Conference on Decision and Control,New York:IEEE,2012:7218–7223.

[21]C.Wang,G.Xie,M.Cao.Forming circle formations ofanonymous mobile agents with order preservation.IEEE Transactions on Automatic Control,2013,58(12):3248–3254.

[22]T.Jim,T.Sugie.Cooperative control for target-capturing task based on a cyclic pursuit strategy.Automatica,2007,43(8):1426–1431.

[23]J.Yan,X.Luo,X.Guan.Multi-target pursuit formation for multiagent systems.Chinese Physics B,2010,20(1):8901–8910.

[24]X.Defago,A.Konagaya.Circle formation for oblivious anonymous mobile robots with no common sense of orientation.Proceedings of the 2nd ACM International Workshop on Principles of Mobile Computing,New York:ACM,2002:97–104.

[25]P.Flocchini,G.Prencipe,N.Santoro.Self-deployment of mobile sensors on a ring.Theoretical Computer Science,2008,402(1):67–80.

[26]J.Marshall,M.Broucke,B.Francis.Formations of vehicles in cyclic pursuit.IEEE Transactions on Automatic Control,2004,49(11):1963–1974.

his B.Sc.degree in Information and Computing Sciences from Ludong University,Yantai,China,in 2013.Currently,he is pursing his M.Sc.degree with Navigation,Guidance and Control in Northeastern University,Shenyang,China.His research interests include formation controland cooperative control.E-mail:adai67@vip.qq.com.

Dan MAreceived the Ph.D.degree in Control Theory and Control Engineering from the Northeastern University,China,in 2007.From 2008 to 2010,she was a postdoctoral fellow at the Northeastern University,China,where she is with School of Information Science and Engineering,and is currently an associate professor.From March 2012 to September 2012,she was a guest professor at the Department of Electrical Engineering,University of Notre Dame.Her current research interests include formation control for multi-agent systems,network-based control systems and hybrid dynamical systems.E-mail:madan@mail.neu.edu.cn.

†Corresponding author.

E-mail:madan@mail.neu.edu.cn.

This work was supported by the National Natural Science Foundation of China(No.61233002)and the Fundamental Research Funds for the Central Universities(No.N120404019).