Discrete-time dynamic graphical games:model-free reinforcement learning solution

Mohammed I.ABOUHEAF ,Frank L.LEWIS ,Magdi S.MAHMOUD ,Dariusz G.MIKULSKI

1.Systems Engineering Department,King Fahd University of Petroleumamp;Mineral,Dhahran-31261,Saudi Arabia;

2.UTA Research Institute,University of Texas at Arlington,Fort Worth,Texas,U.S.A.;

3.State Key Laboratory of Synthetical Automation for Process Industries,Northeastern University,Shenyang Liaoning 110819,China;

4.Ground Vehicle Robotics(GVR),U.S.Army TARDEC,Warren MI,U.S.A.

Received 31 December 2013;revised 2 January 2015;accepted 15 January 2015

Discrete-time dynamic graphical games:model-free reinforcement learning solution

Mohammed I.ABOUHEAF1†,Frank L.LEWIS2,3,Magdi S.MAHMOUD1,Dariusz G.MIKULSKI4

1.Systems Engineering Department,King Fahd University of Petroleumamp;Mineral,Dhahran-31261,Saudi Arabia;

2.UTA Research Institute,University of Texas at Arlington,Fort Worth,Texas,U.S.A.;

3.State Key Laboratory of Synthetical Automation for Process Industries,Northeastern University,Shenyang Liaoning 110819,China;

4.Ground Vehicle Robotics(GVR),U.S.Army TARDEC,Warren MI,U.S.A.

Received 31 December 2013;revised 2 January 2015;accepted 15 January 2015

This paper introduces a model-free reinforcement learning technique that is used to solve a class of dynamic games known as dynamic graphical games.The graphical game results from multi-agent dynamical systems,where pinning control is used to make all the agents synchronize to the state of a command generator or a leader agent.Novel coupled Bellman equations and Hamiltonian functions are developed for the dynamic graphical games.The Hamiltonian mechanics are used to derive the necessary conditions for optimality.The solution for the dynamic graphical game is given in terms of the solution to a set of coupled Hamilton-Jacobi-Bellman equations developed herein.Nash equilibrium solution for the graphical game is given in terms of the solution to the underlying coupled Hamilton-Jacobi-Bellman equations.An online model-free policy iteration algorithm is developed to learn the Nash solution for the dynamic graphical game.This algorithm does not require any knowledge of the agents’dynamics.A proof of convergence for this multi-agent learning algorithm is given under mild assumption about the inter-connectivity properties of the graph.A gradient descent technique with critic network structures is used to implement the policy iteration algorithm to solve the graphical game online in real-time.

Dynamic graphical games,Nash equilibrium,discrete mechanics,optimal control,model-free reinforcement learning,policy iteration

DOI 10.1007/s11768-015-3203-x

1 Introduction

This paper develops an online model-free policy iteration solution[1,2]for a class of discrete-time dynamic graphical games developed in[3].The information flow between the agents is governed by a communication graph.Continuous-time differential graphical games have been developed in[4].Novel model-free policy iteration algorithm is developed to learn Nash solution for graphical game in real-time.This paper brings together cooperative control,optimal control,game theory,and reinforcement learning techniques to find online solutions for the graphical game.

The optimal control theory uses the Hamilton-Jacobi-Bellman(HJB)equation whose solution is the optimal cost-to-go function[5,6].Discrete-time canonical forms forthe Hamiltonian functions are found in[7–9].The cooperative control problems involve the consensus control problems and the synchronization control problems[10–16].The agents synchronize to uncontrollable node dynamics in the cooperative consensus problem.While in the synchronization control problem,the control protocols are designed such that each agent reaches the same state[17–21].

Game theory provides a solution framework formultiagent control problems[22].Non-cooperative dynamic game theory provides an environment for formulating multi-player decision control problems[23].Each agent finds its optimal control policy through optimizing its performance index independently[23].Offline solutions for the games are given in terms of the respective coupled Hamilton-Jacobi(HJ)equations[23–25].

Approximate dynamic programming(ADP)is an approach to solve the dynamical programming problems[1,2,26–31].ADP combines adaptive critics and reinforcement learning(RL)techniques,with dynamic programming[2].ADP techniques are developed to solve the optimal control problem online in[2]and offline in[29].Morimoto et al used the concept of Q-learning to solve the differentialdynamic programming[32].Landelius,used the action dependent heuristic dynamic programming(ADHDP)to solve the linear quadratic optimal control problem and showed that the solution is equivalent to iterating the underlying Riccati equations[33].RL is concerned with learning from interaction in a dynamic environment[34,35].RL algorithms are used to learn the optimal control solutions for dynamic systems in real-time[1,2,34,36,37].These algorithms involve policy iteration(PI)or value iteration(VI)techniques[29,36,38–42].New policy iteration approach employed ADP to find online solutions for the continuous-time Riccati equations in[43].Policy iteration solution for the adaptive optimal control problem can be obtained by relaxing the HJB equation to the equivalent optimization problem[44].RL algorithms are used to solve multi-player games for finite-state systems in[40–42]and to learn online in real-time the solutions for the optimal control problems of the differential games in[36–38,45,46].Actor-critic neural network structures are used to solve the graphical game using heuristic dynamic programming(HDP)in real-time[3].

In this paper,the dynamic graphical game developed herein,is a special case of standard dynamic game[23]and explicitly captures the structure of the communication graph topology.The ADHDP structure for single agent[2]is extended for the case of the dynamic graphical games and it is used to solve the game in a distributed fashion unlike[23].Usually,offline methods are employed to find Nash solutions for the games in terms of the coupled HJ equations(which are difficult to solve)[23–25].Herein an online adaptive learning solution for the graphical game is given in terms of the solution to a set of novel coupled graphical game Hamiltonian functions and Bellman equations.Policy iteration convergence proof for the graphical game is given under mild condition aboutthe graph interconnectivity.In[42],the Q learning update rule will converge to the optimal response Q-function as long as all the other agents converge in behavior.The developed online adaptive learning solution allows model-free tuning of the critic networks,while partial knowledge about the game was required in[3],[4],and[37].

The paper is organized as follows.Section 2 reviews the synchronization control problem for multi-agent systems on graphs.Section 3 formulates the dynamic graphical game in terms of the coupled Bellman equations and the respective Hamiltonian functions.This section finds the solution for the graphical game in terms of the solution to a set of coupled HJB equations.Section 4 shows that,the Nash solution for the graphical game is given in terms of the underlying coupled(HJB)equations.Section 5 develops an online adaptive model-free policy iteration algorithm to solve the dynamic graphical game in real-time along with its convergence proof.Section 6 implements the online policy iteration algorithm using critic network structures.

2 Synchronization of multi-agent systems on graphs

This section reviews the synchronization control problem on communication graphs.

2.1 Graphs

2.2 Synchronization and tracking error dynamics

The dynamics of each agentiis given by

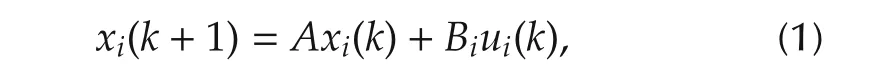
wherexi(k)∈Rnis the state vector of agenti,andui(k)∈Rmiis the control input vector for agenti.

A leader agentv0has the dynamics[47]x0(k)∈Rngiven by

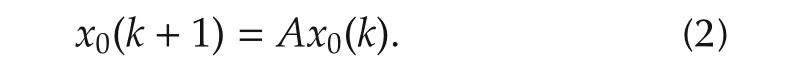
To study synchronization on graphs,define the local neighborhood tracking error[48]εi(k)∈ Rnfor each agentias

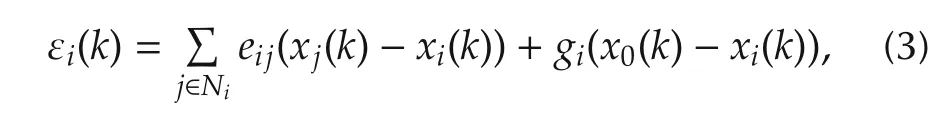
wheregiis the pinning gain of agenti,which is nonzerogigt;0 if agentiis coupled to the leader agentx0[18].

The overall tracking error vector ε =[εT1εT2···εTN]Tis given by

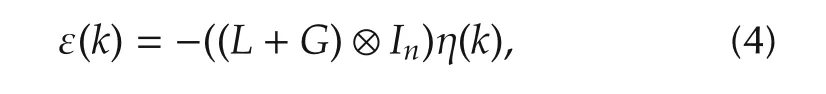
whereG=diag{gi}∈ RN×Nis a diagonal matrix of the pinning gains.The global synchronization error vector η[13]is given by

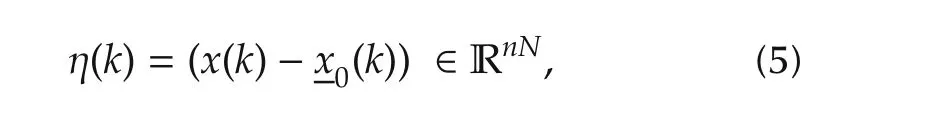
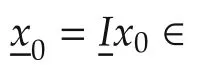
The graph is assumed to be strongly connected and the pinning gain isgigt;0 for at least one agenti,then the graph matrix(L+G)is nonsingular[48].The synchronization error is bounded such that

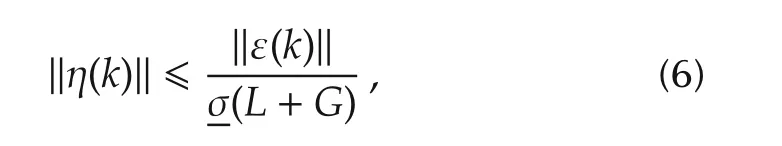
Our objective is to minimize the local neighborhood tracking errors εi(k),which in view of(6)will guarantee approximate synchronization.

The local neighborhood tracking error dynamics for agentiare given by

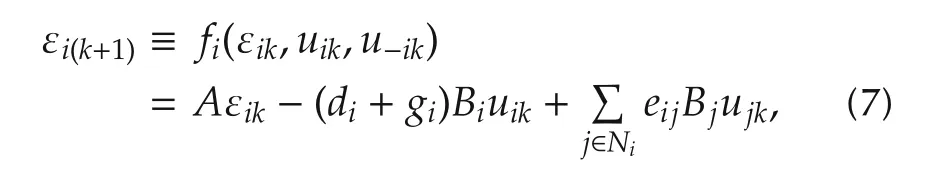
whereu−iare the control actions of the neighbors of each agenti u−i={u j|j∈Ni}.

Define the group of control actions of the neighbors of each agentiand the control actions of the neighbors to the neighbors of each agentiasu−i,−{−i}={u j|j∈Ni,N{−i}}and the actions of all the agents in the graph excludingiasu¯i={u j|j∈N,j?i}.

3 Multi-playercooperative gameson graphs

In this section,solutions for the dynamic games on graphs are developed.These dynamic interacting games are based on the error systems(7),which are locally coupled in the sense that they are driven by the agent’s control actions and those of its neighbors.The solution for the dynamic graphical game is given in terms of the solution to a set of novel coupled Hamiltonian functions and Bellman equations developed herein.The ADHDP structure for single agent[2]is extended to solve the dynamic graphical game without knowing any of the agents’dynamics.

3.1 Graphical games:performance evaluation

Graphical games are based on the interactions of each agentiwith the other players in graph.The local neighborhood dynamics(7)arise from the nature of synchronization problem for dynamic systems on communication graphs.Therefore,in order to define a dynamic graphical game,the local performance index for each agentiis written as

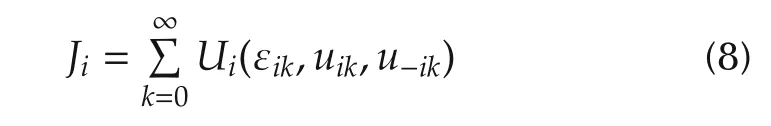
and the utility functionUifor each agentiis given by

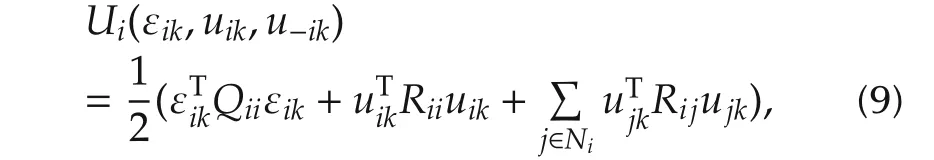
whereQii0 ∈ Rn×n,Riigt;0 ∈ Rmi×mi,andRijgt;0 ∈Rmj×mjare symmetric time-invariantweighting matrices.

For the multi-player graphical game,it is desired to determine the optimal non-cooperative solutions such that the following distributed coupled optimizations are solved simultaneously,

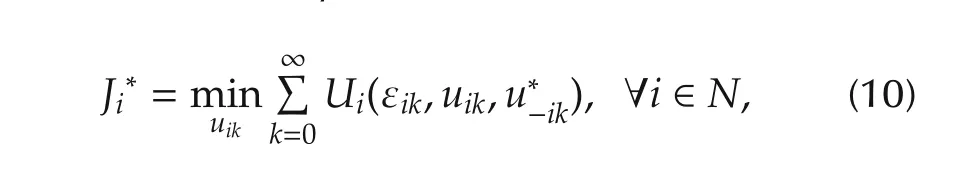
Given fixed policies(μil,μ−il)of agentiand its neighbors,the value function for each agentiis given by

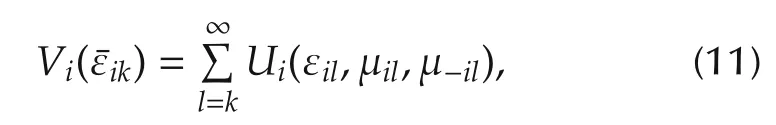
Remark 1The performance index(8)measures the performance of each agenti.The value function for each agenti(11)captures local information.Thus,the solution structure of the value function will be given in terms of the local vector¯εik.This value structure will be used in the mathematical setup for the graphical game.

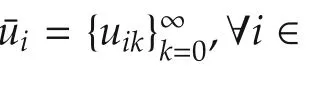
Def i nition2The dynamic graphical game with local dynamics(7)and performance indices(8)is well-formed ifRij?0eij∈E.

3.2 Hamiltonian function for graphical games

Given the dynamics(7)and the performance indices(8),define the Hamiltonian function[6]of each agentias

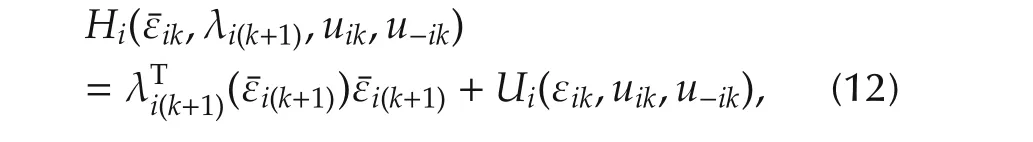
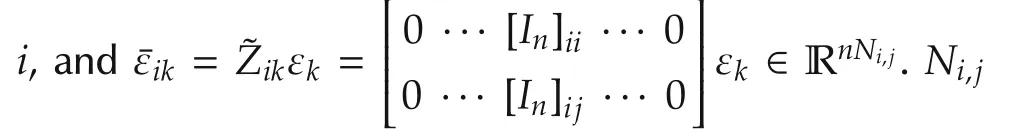
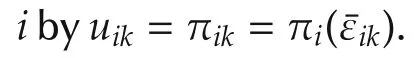
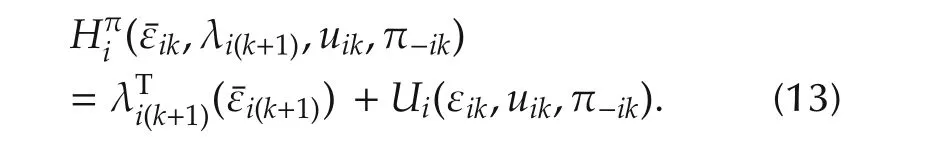
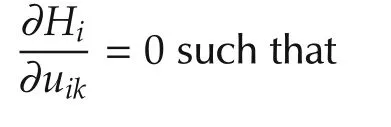
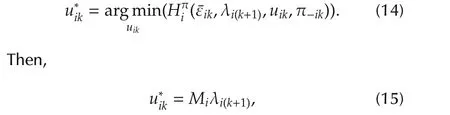
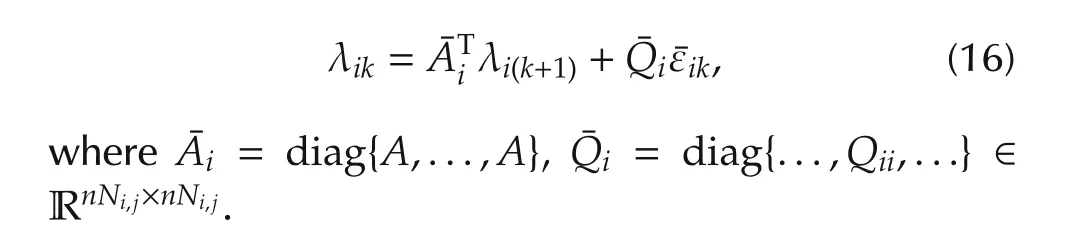
3.3 Bellman equation for graphical games

Herein Bellman optimality equations are developed to solve the graphical games.The value function(11)given stationary admissible policies yields the dynamic graphical game Bellman equations such that

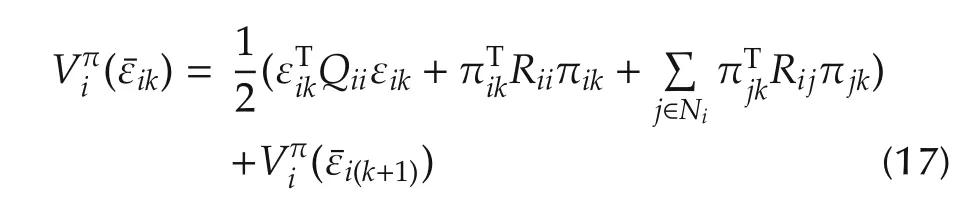
with initial conditionsVπi(0)=0.

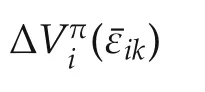
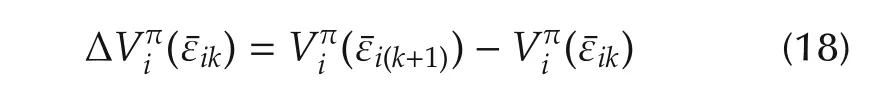
and its gradient as

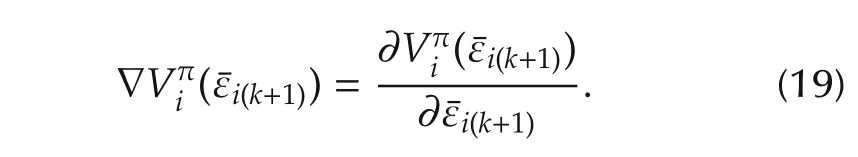
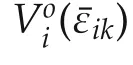
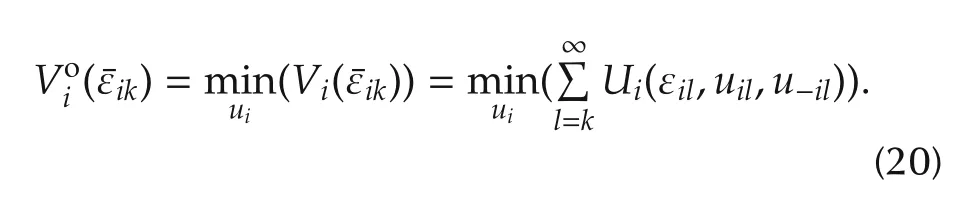
Given stationary admissible polices for the neighbors of agenti.Applying the Bellman optimality principle yields

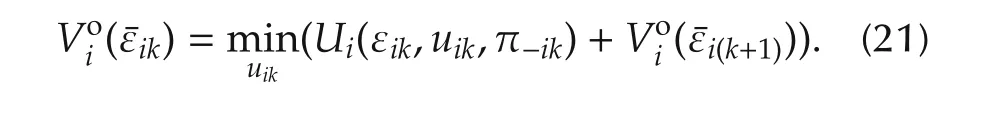
Consequently,the optimal control policy for each agentiis given by

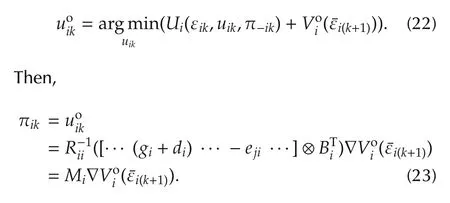
Substituting(23)into(21)yields the graphicalgame Bellman optimality equations

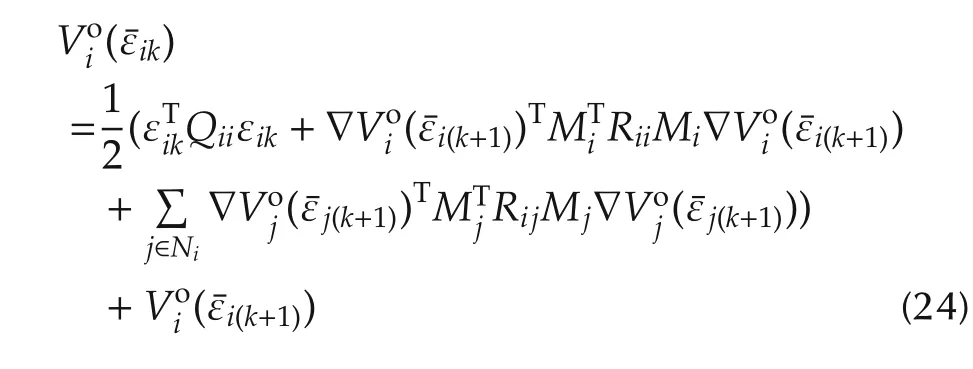
3.4 Q-function based Bellman equations

Herein,ADHDP structure for single agent is extended to formulate and solve the dynamic graphicalgame without knowing any of the agents’dynamics where only local measurements are used.The solution for the graphical game is given in terms of the solution to a set of coupled DTHJB equations.

The Q-function for each agentiis defined as follows:

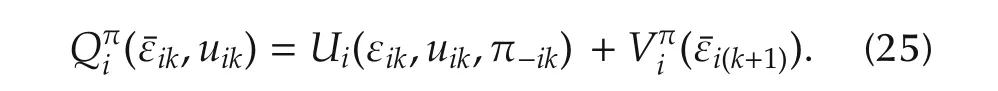
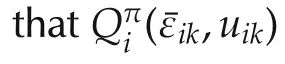
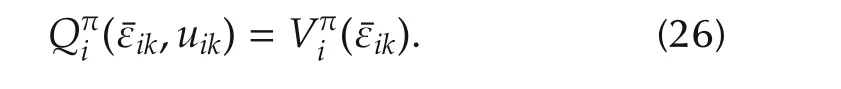
Therefore,the best response Bellman equation is given by

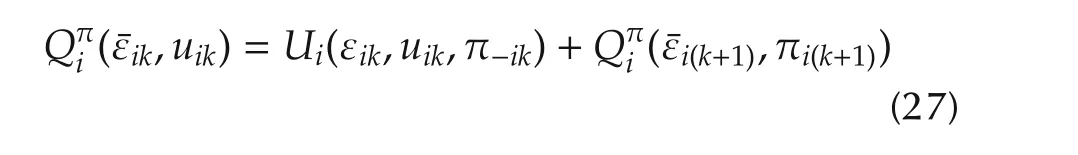
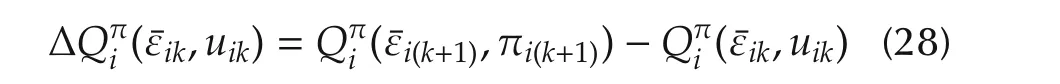
and its gradient as

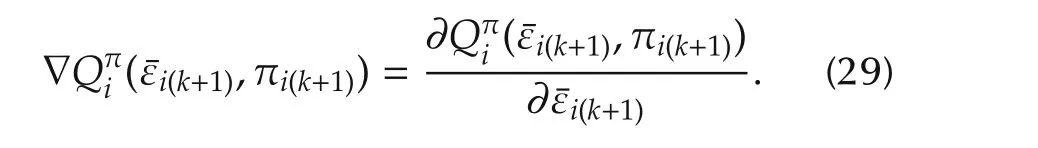
The optimal control policy for each agentiis given such that

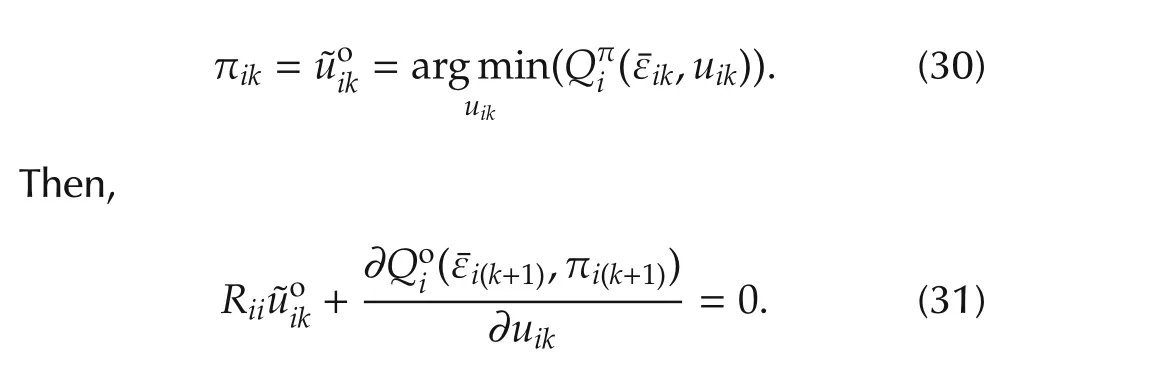
Therefore,the optimal control policy is given by

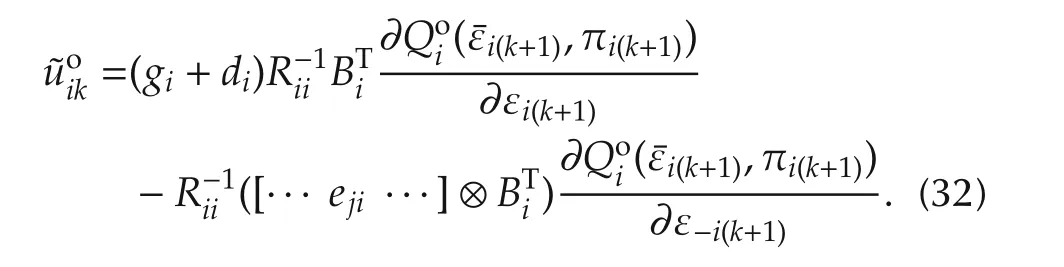
Rearranging this equation yields

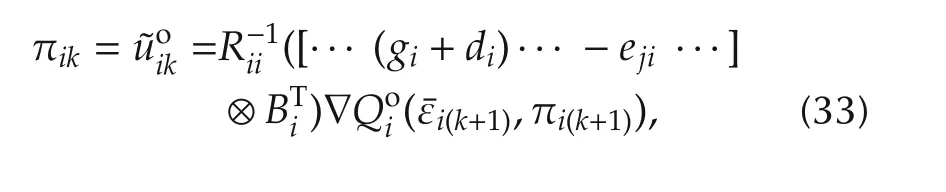
which is the same as(23).Then,

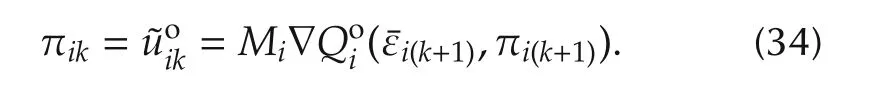
Thus,the best response Bellman optimality equation based on the Q-function(25)and optimal policies(34)is given by

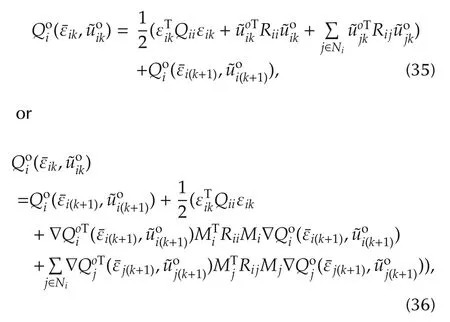
which is equivalent to(24).

3.5 Coupled Hamilton-Jacobi-Bellman equations

The Hamilton-Jacobi theory[9]is used to relate the Hamiltonian functions(13)and the Bellman equations(27).

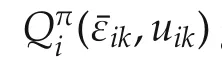
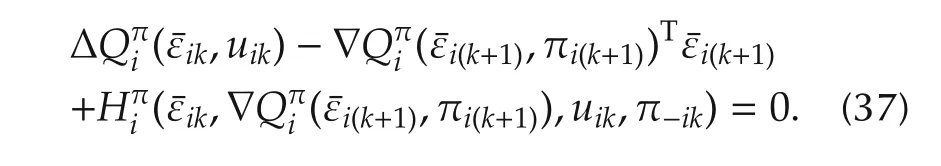
This equation provides the motivation for defining the costate variable λi(k+1)in terms of the Q-function such that

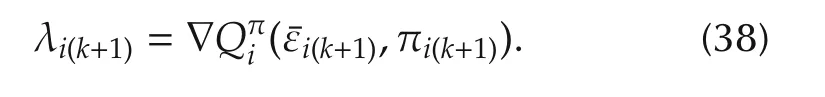
The optimal control policy based on the Bellman optimality equation(27)is given by(34).The next result relates the Hamiltonian(13)along the optimal trajectories and the Bellman optimality equation(36).

Theorem 1(Discrete-time coupled HJB equation)

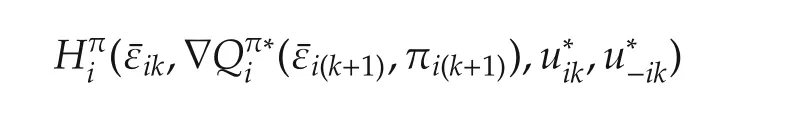
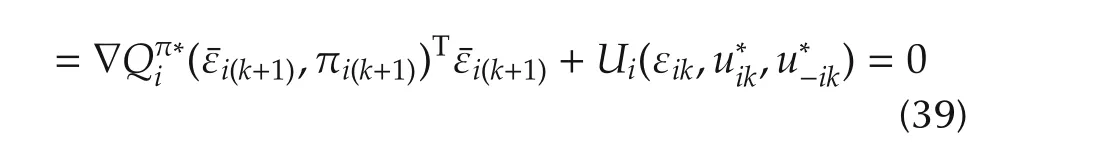
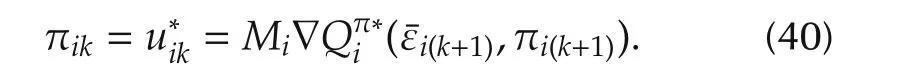
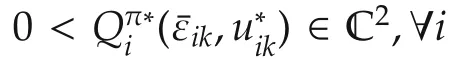
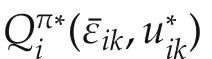
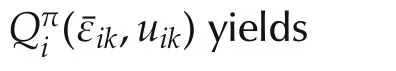
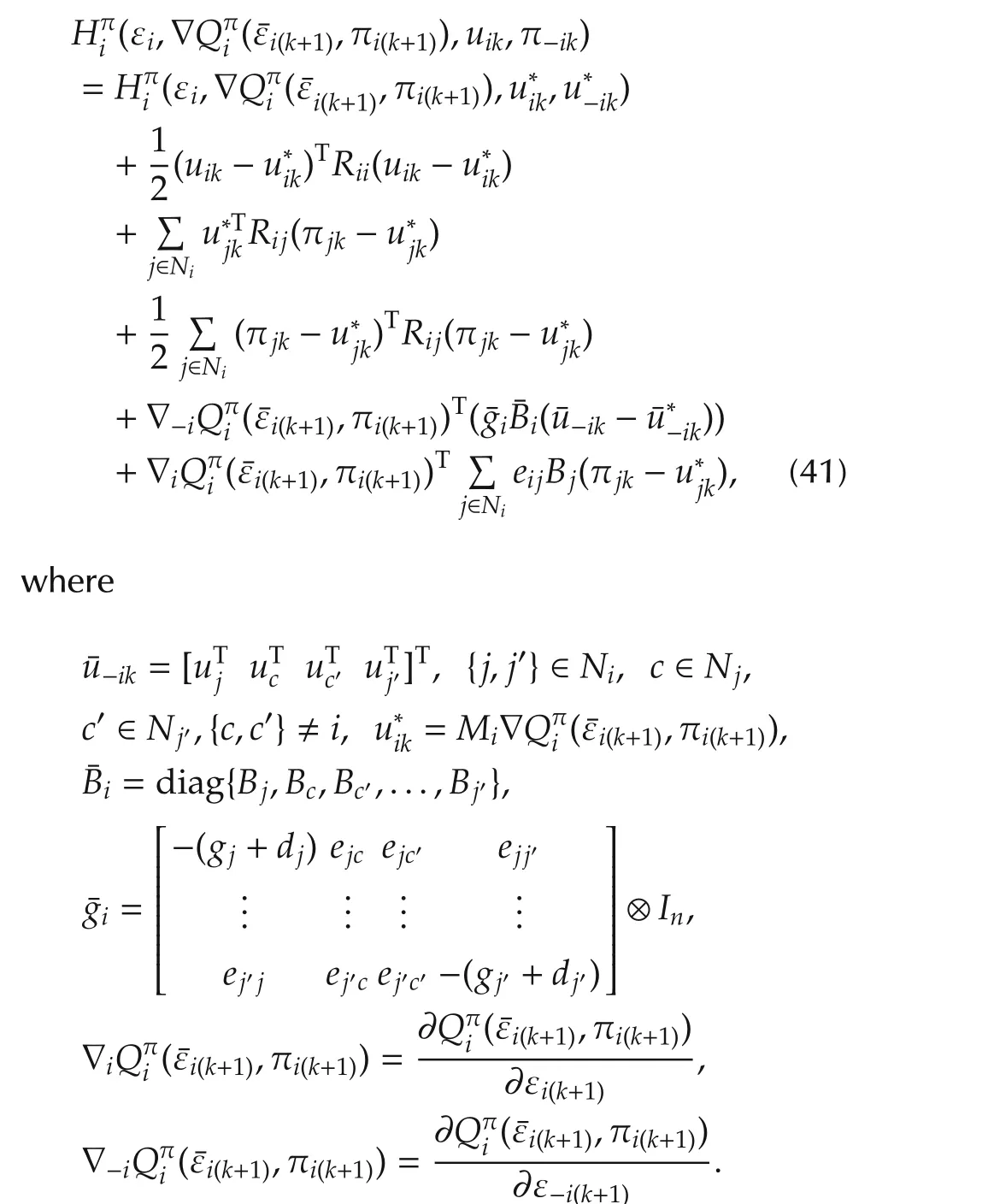
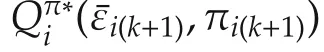
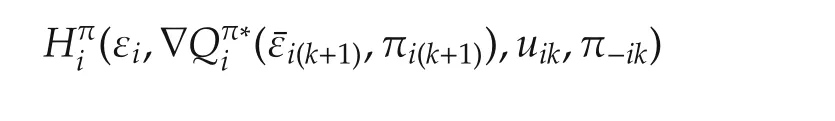
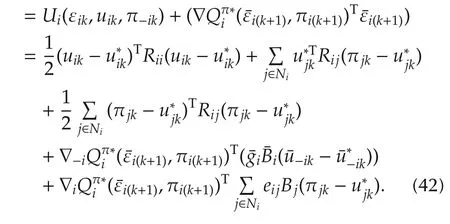
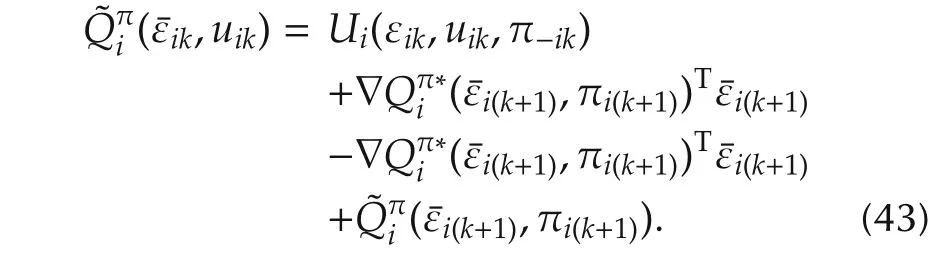
Introducing the Hamiltonian(42)into this equation yields

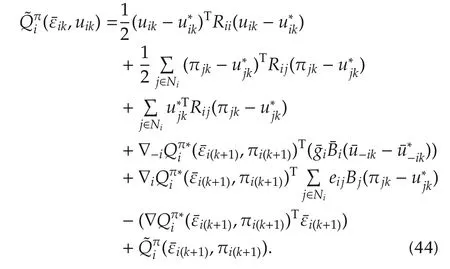
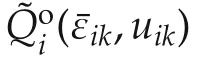
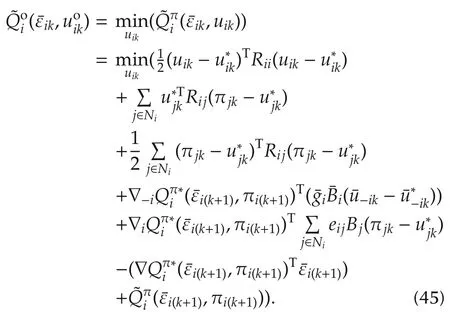
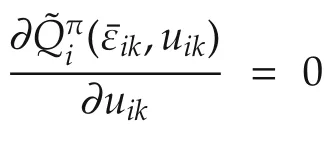
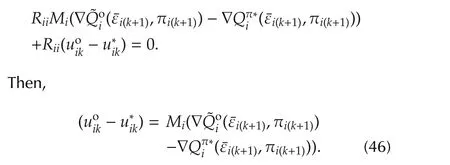
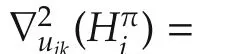
Equations(46)and(16)yield

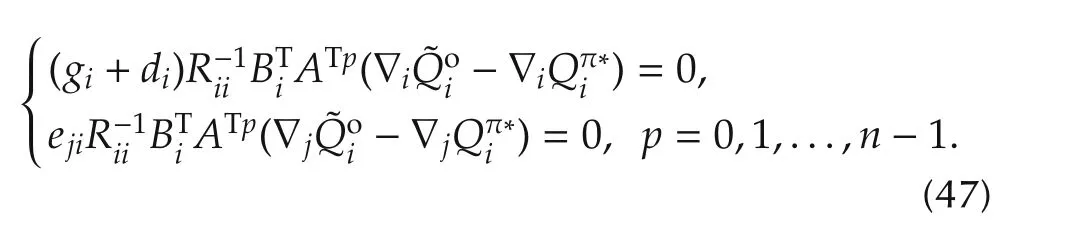
The reachability matrix

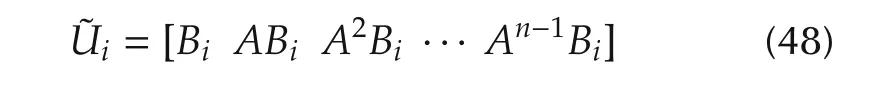
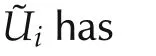
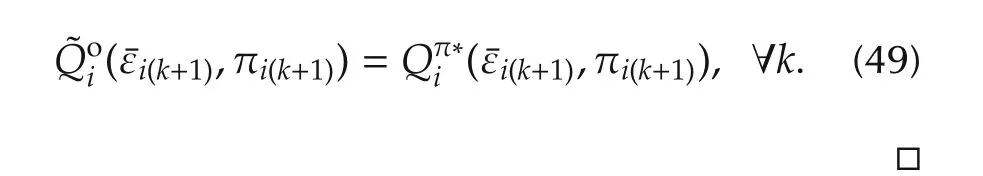
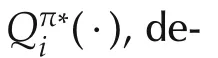
4 Nash solution for the dynamic graphical game

The objective of the dynamic graphical game is to solve the non-cooperative minimization problems(20),which lead to the Bellman optimality equations(36).In this section,it is shown that,the solution of the coupled Bellman optimality equations(36)is a Nash equilibrium solution for the dynamic graphical game.

4.1 Nash equilibrium for the graphical games

Nash equilibrium solution for the game is defined as follows[23]

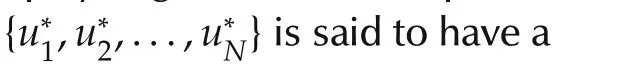
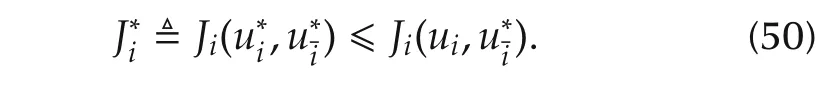
4.2 Stability and Nash solution for the graphical games

Stable Nash solution for the dynamic graphical game is shown to be equivalent to the solution of the underlying coupled Bellman optimality equations(24)or(36).

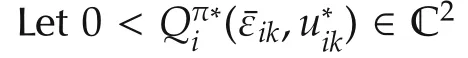
a)all agents synchronize to the leader’s dynamics(2);

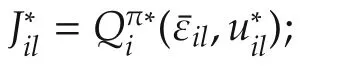
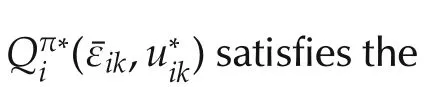
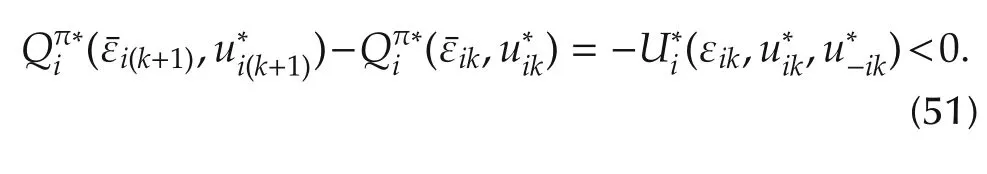
b)Using Theorem 1 and DTHJB(39),then the Hamiltonian(41)for arbitrary control policies is given by

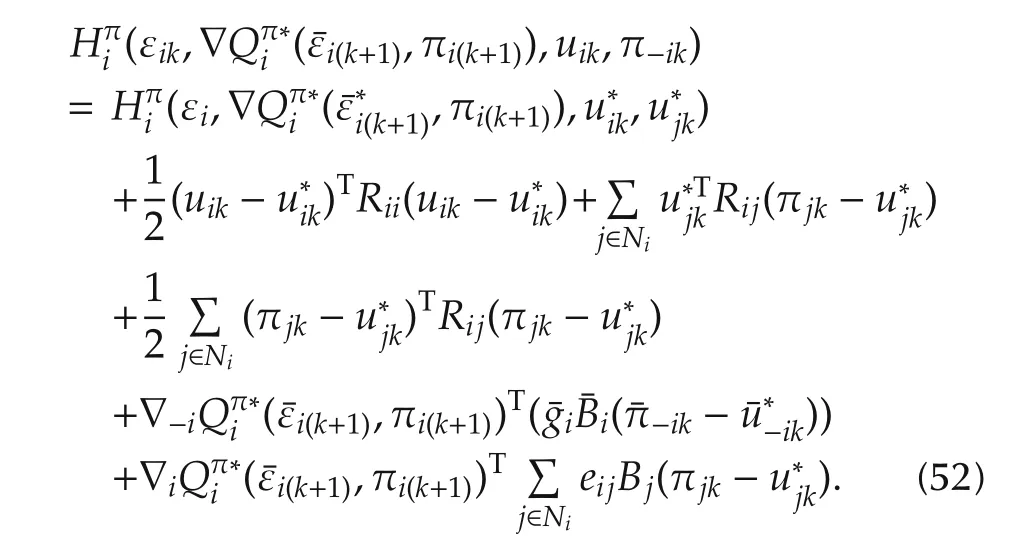
The performance index at time indexlis given by

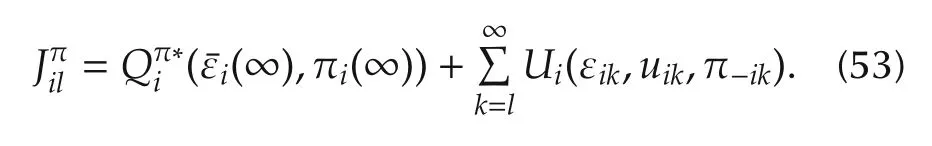
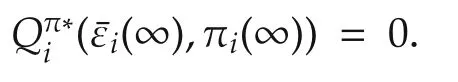
Rearranging(53)yields

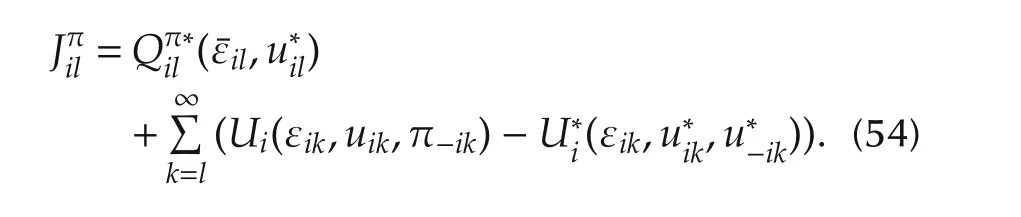
The Hamiltonian for arbitrary control inputs is given by

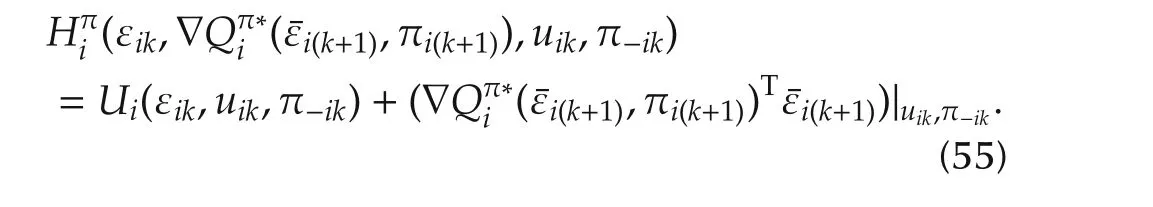
The Hamiltonian for optimal control inputs is given by

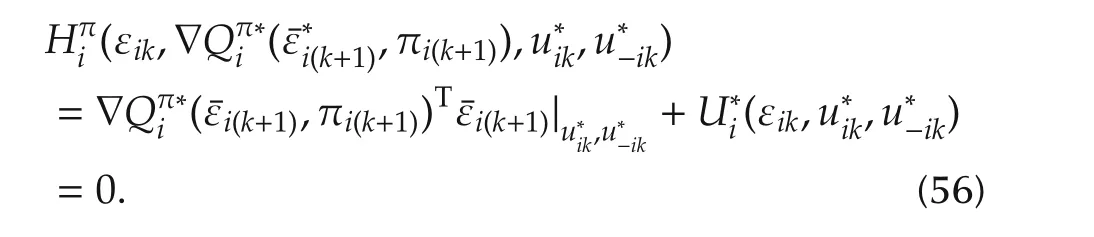
Using(55)and(56)in(54)yields

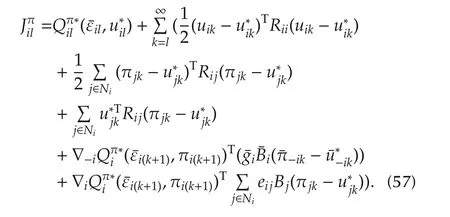
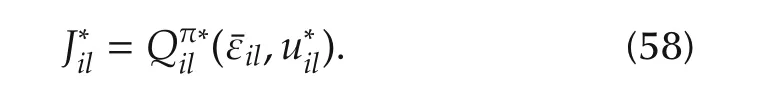
c)Given that the summation of the performance index(54)is always positive for arbitrary control policies such that

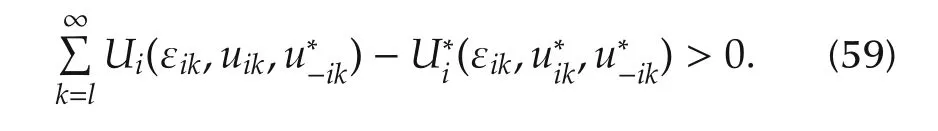
Then,according to(59),the argument of the performance index(57)is positive for arbitrary control policy.Then,(59)and(54)yield

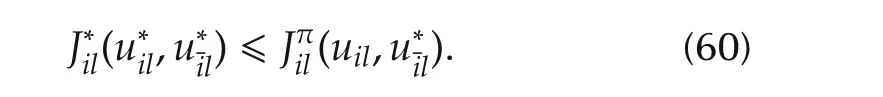
Therefore,Nash equilibrium exists according to Definition 3.

5 Model-free reinforcement learning solution

In this section,an online model-free policy iteration algorithm is developed to solve the discrete-time dynamic graphical games in real-time.This is a cooperative version of the ADP single agent’s methods intro

duced in[1,2].Specifically,the single agent(ADHDP)algorithm is extended to solve the multi-player dynamic graphical game.

The Q-function is expressed in terms of the agent control input,state of each agenti,and the states of its neighbors such that

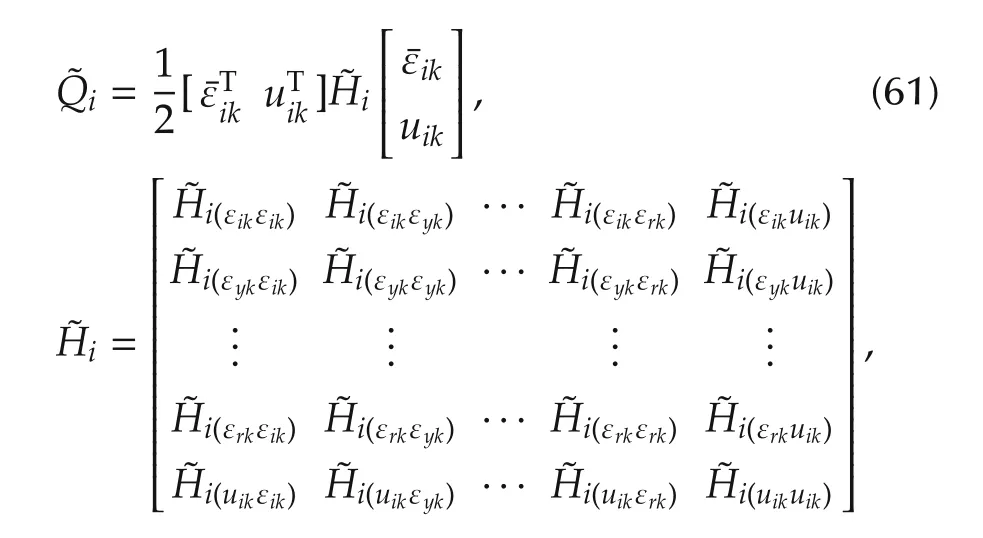
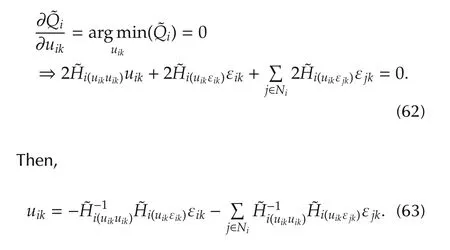
The following algorithm solves the Bellman optimality equations(36)for the optimal game values and policies.

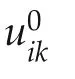
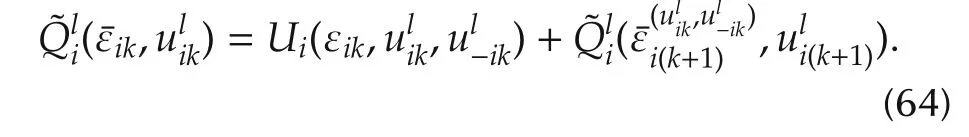
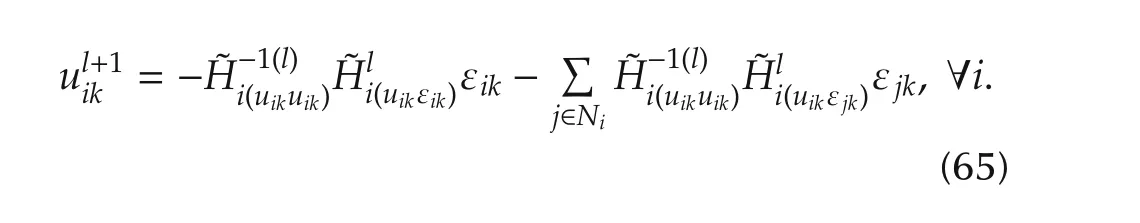
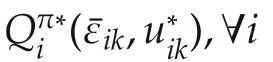
Remark 3This algorithm does not require the knowledge of any of the agents’dynamics in the systems(7).

Remark 4The Policy improvement step(65)in Algorithm 1 does not require the graph to be undirected as previously imposed by the optimal policy structure(34)where the out-neighbor information are required.Thus,step(65)enables Algorithm 1 to solve the dynamic graphical games with directed or undirected graph topologies.

Remark 5To solve the Bellman equations(64),numerous instances of(64)must be obtained at successive time instants.For these equations to be independent,a persistence of excitation condition is needed as per standard usage.This is further discussed in Remark 6 immediately before Section 6.1.

The following theorem provides the convergence proof for Algorithm 1 when all agents update their policies simultaneously.

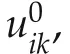
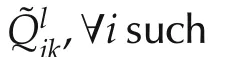
Proofa)Equations(27)or(64)yield,

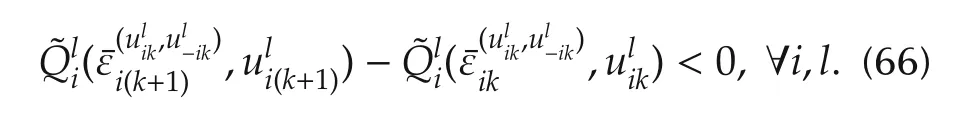
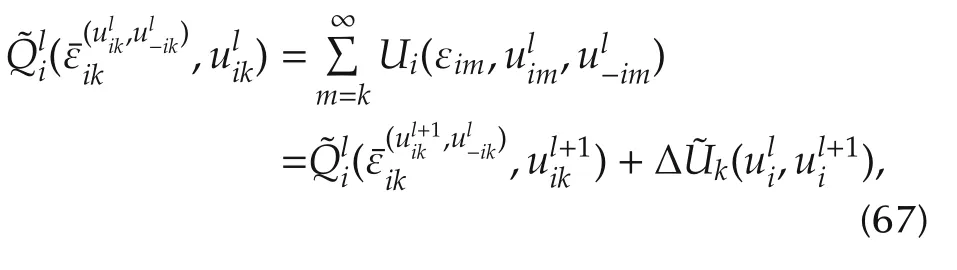
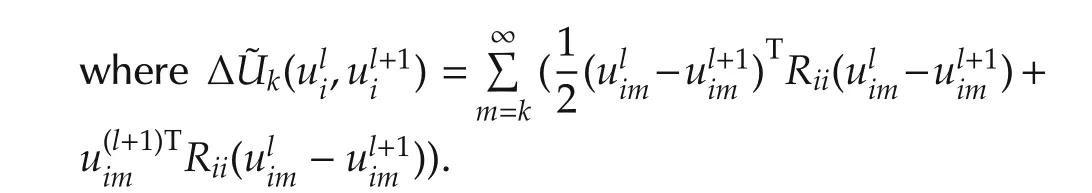
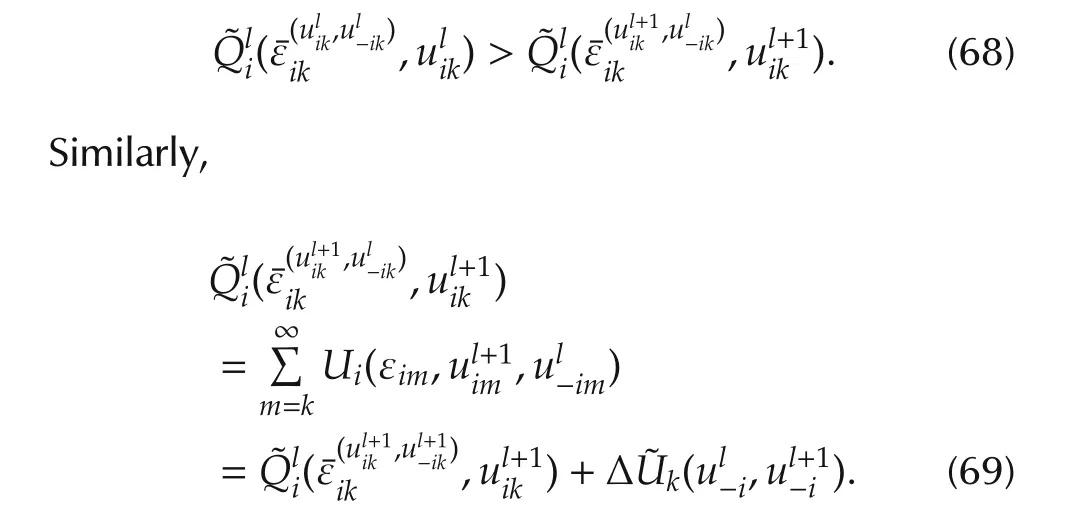
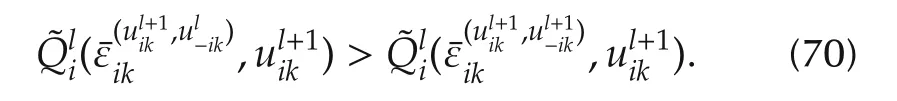
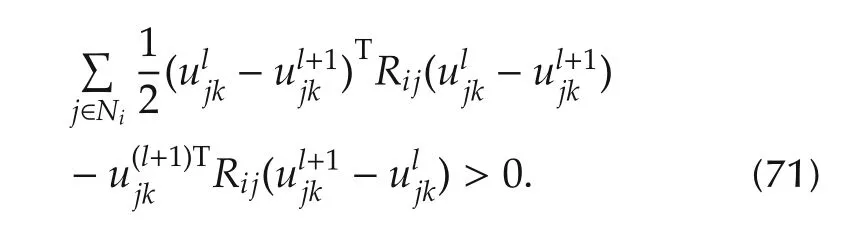
Using the norm properties on this inequality yields

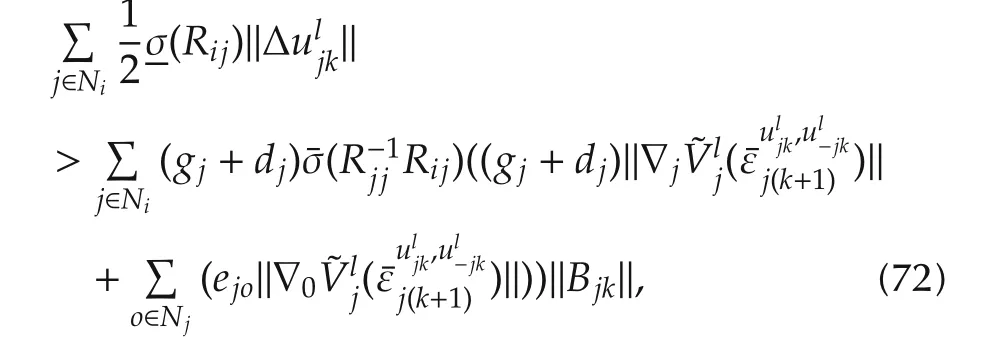
Under the assumption(72).Inequalities(68)and(70)yie ld

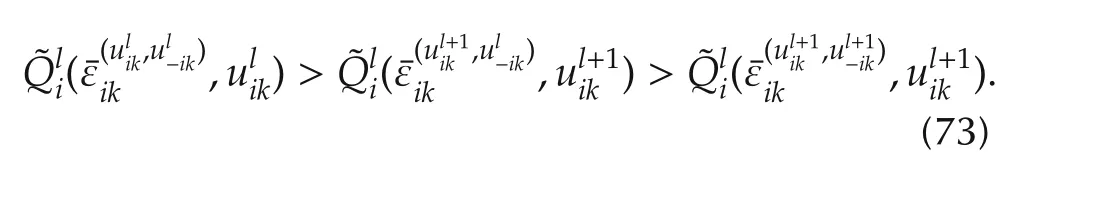
b)Equation(66)yields

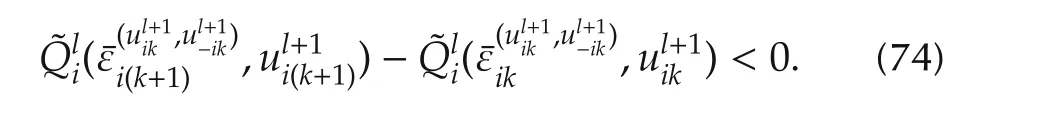
Equation(26)or(64)yields

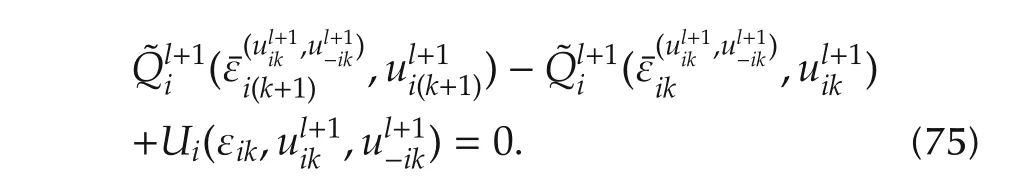
Equations(74),(75),and the assumption(72)yield

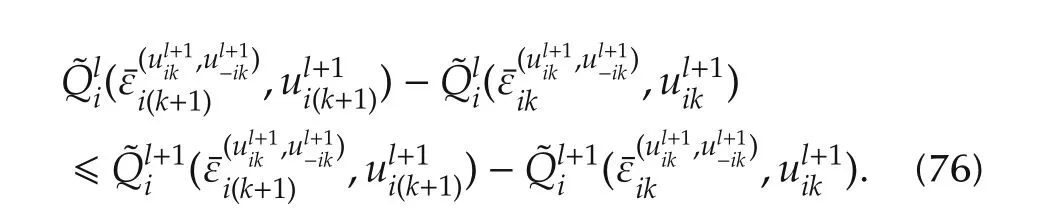
Applying the summation on(76)such that

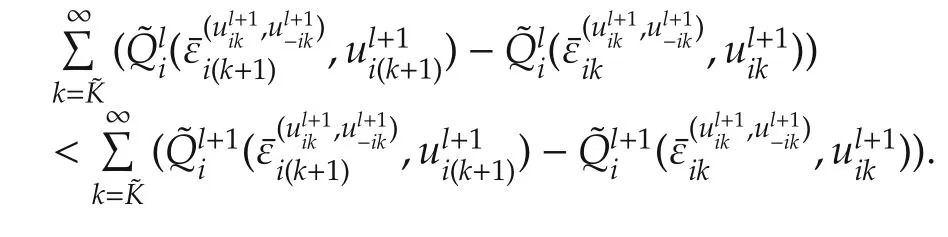
This reduces to

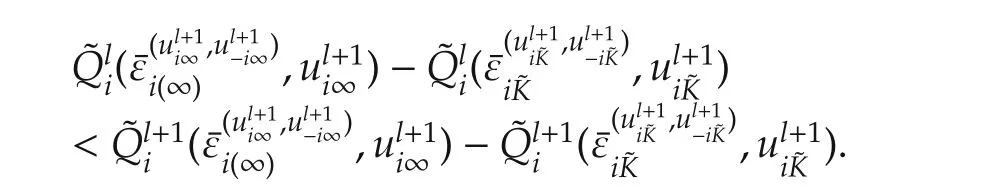
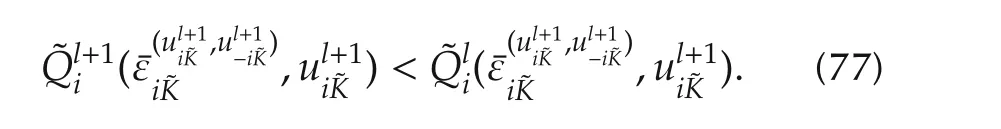
Therefore,by induction(77)yields

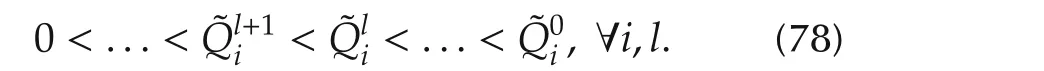
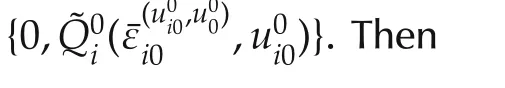
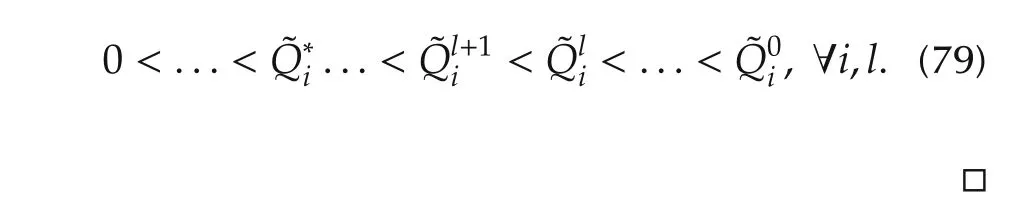
This result shows that Algorithm 1 converges when the performance indices are suitably chosen.

6 Critic network solutions for the graphical games

It is not clear how to best implement Algorithm 1.In the single-agent case the implementation details do not matter too much.Proper implementation of Algorithm 1 isneeded formulti-agentgraphicalgames where numerous agents are learning.There are different methods that are used to implement Policy Iteration Algorithm 1,these involve least squares,batch least squares,Actor-Critic neural network,etc.Herein,we present a novel method for implementing Algorithm 1 for multi-agent learning on graphs,wherein all agents learn simultaneously and computationsare reduced.Algorithm 2 willbe formulated such that it uses only critic networks.This is the easiest way to implement Algorithm 1,without the difficulties that are associated with the other methods.Algorithm 2 will use gradient descent to tune the weights of the critic at each iteration.

This section develops an online model-free critic network structure based on the Q-function value approximation(61)that is used to solve the dynamic graphical gamesin real-time.This ismotivated by the graph games Algorithm 1.Each agentihas its own critic to perform the value evaluation using local information.The policy of each agentiis improved using(65).

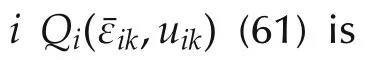
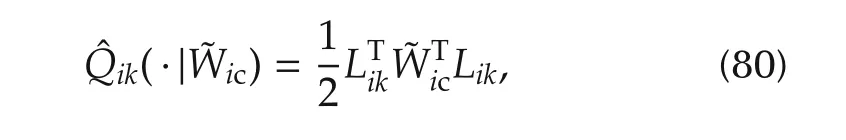
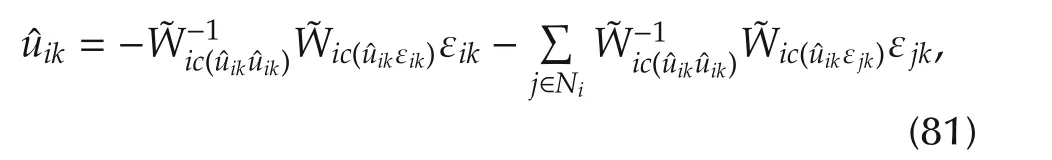
The policy iteration Algorithm 1 requires that the approximation of the Q-function(80)to be written as

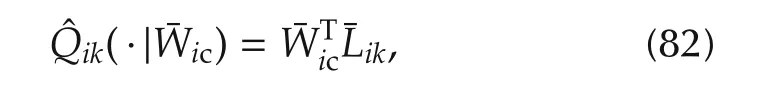
Using(82),the Bellman equation(64)is written such that

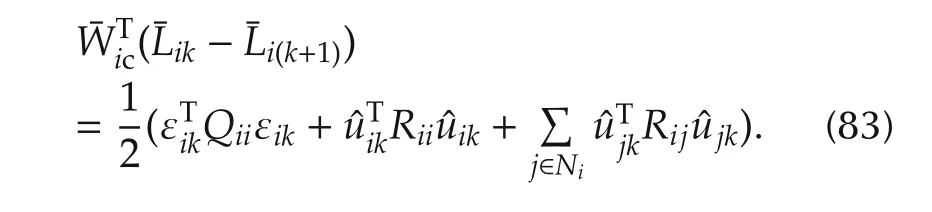
The critic network structure for each agentiperforms the evaluation(64).The policy improvement(65)depends on the evaluated value function(64).

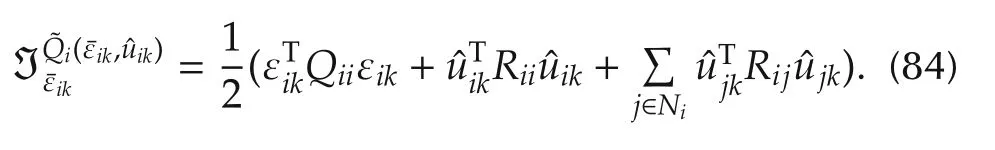
The neural network approximation error is given by

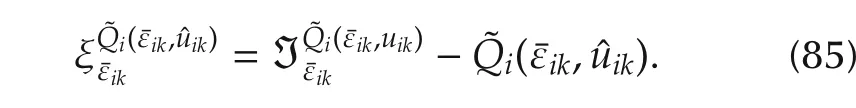
The square sum of the approximation error for each neural networkican be written as

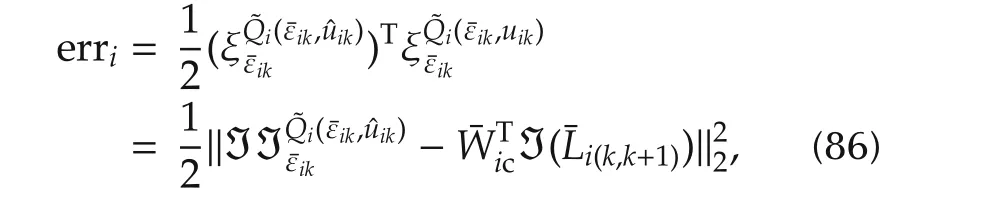
The change in the critic neural network weights is given by gradient descent on this function whose gradient is

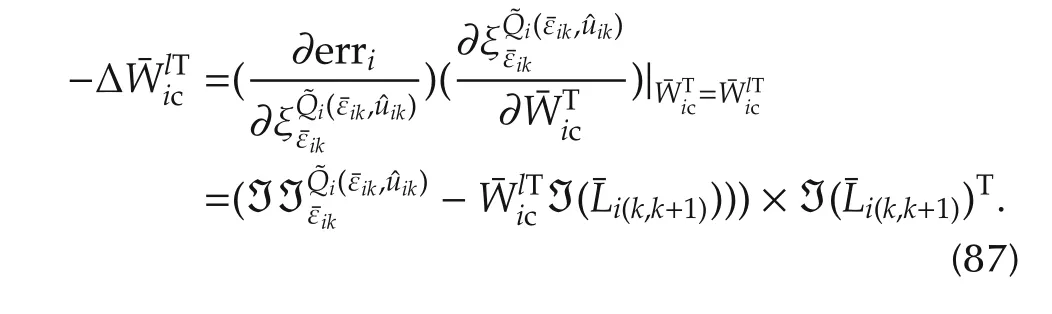
Therefore,the update rules for the network weights are given by

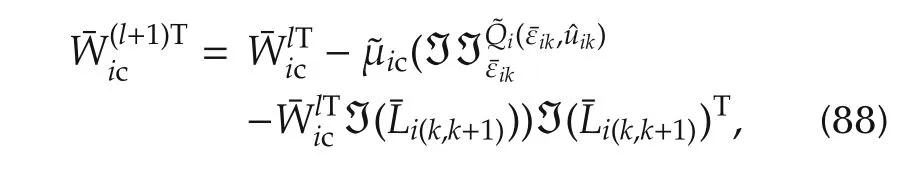
Remark 6To solve for the weights proximated Bellman equation(83),numerous instances of(83)must be obtained at successive time instants.For these equations to be independent,a persistence of excitation condition is needed.Our approach uses the gradient descent algorithm(87)to solve these equations,and hence a PE condition is also needed.This can be achieved by adding probing noise to the control,which is decayed to zero with time as the solution to(83)is learned.

6.1 Network weights online tuning in real-time

The following algorithm is used to tune the critic network weights in real-time using data measured along the system trajectories.

Algorithm 2(Network weights online tuning)

2)Do Loop(literations).

Do Loop(siterations).

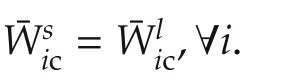
2.2)Critic network weights update rule

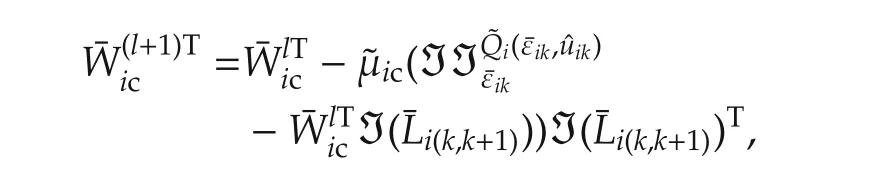
Remark 7Algorithm 2 uses gradient descent technique to tune the critic network weights at each iteration.Theorem 3 proved the convergence of Algorithm 1 at each step.Assuming that the gradient descent algorithms converge exactly at each iteration,then Algorithm 2 at each step solves first the Bellman equation(64)and then the action update(65).Unfortunately,gradient descent cannot always be guaranteed to converge to the exact solutions in the approximation structures.However,simulations have shown the effectiveness of this algorithm.

6.2 Graphical game example and simulation results

In this section the graphical game problem is solved online in real-time using Algorithm 2.Simulations are performed to verify the proper performance of Algorithm 2.

Consider the directed graph with four agents shown in Fig.1.

The data of the graph example are given as follows:

Agents’dynamics:

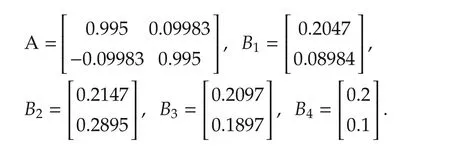
Pinning gains:g1=0,g2=0,g3=0,g4=1.

Graph connectivity matrix:e12=0.8,e14=0.7,e23=0.6,e31=0.8.

Performance index weighting matrices:Q11=Q22=Q33=Q44=I2×2,R11=R22=R33=R44=1,R13=R21=R32=R41=0,R12=R14=R23=R31=1.

The learning rates are˜μic=0.0001,∀i.

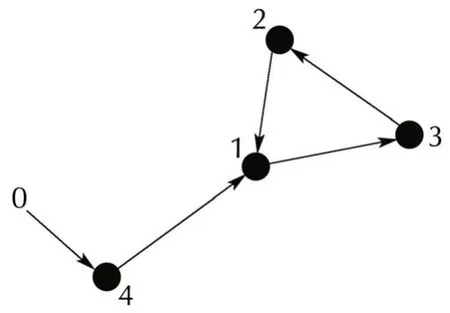
Fig.1 Graphical game example.

Fig.2 shows that,the neighborhood tracing error dynamics go to zero.Fig.3 shows that,the dynamics of the agents synchronize to the leader while preserving the optimal behavior.Fig.4 shows a 3D phase plane plot of the agents’dynamics.This figure shows that,the agents synchronize to the leader agent’s dynamics.These figures show that Algorithm 2 yields stability and synchronization to the leader’s state.As shown in Remark 7,the gradient descent technique is assumed to converge at each step.Thus,a slow learning rate is chosen.The Policy Iteration Algorithm 2,guarantees the convergence of the agents to the leader’s dynamics.For this graphical example,outer loop iterations in Algorithm 2l=60 tol=70 are enough to maintain the synchronization.

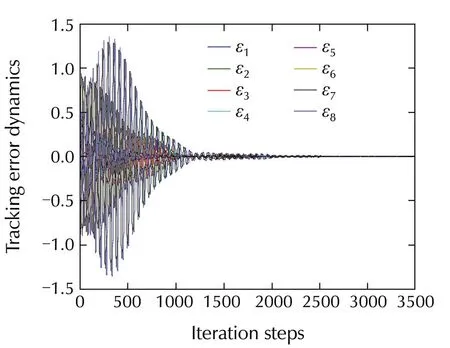
Fig.2 Tracking error dynamics.

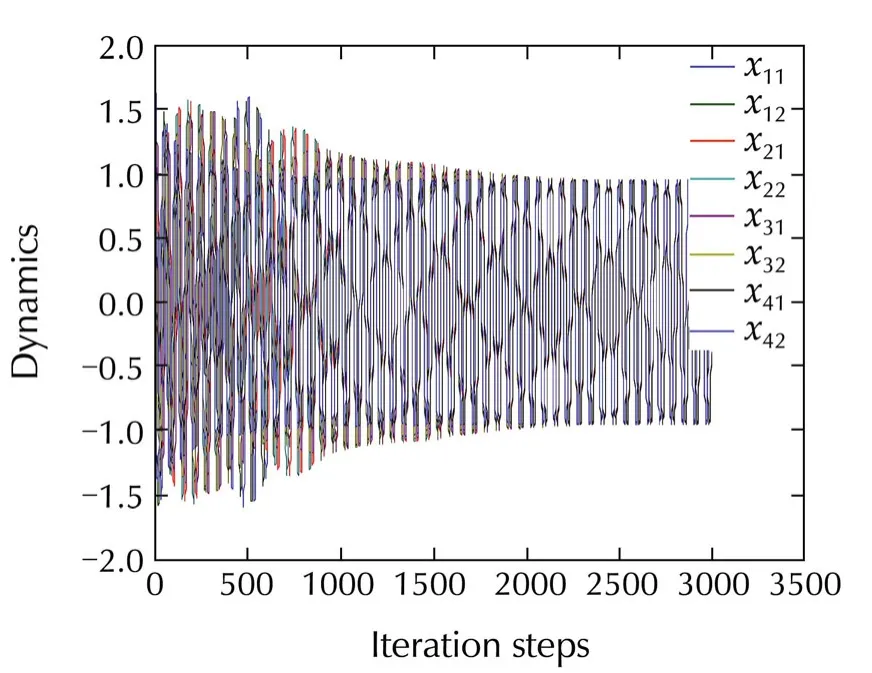
Fig.3 Agents’dynamics.

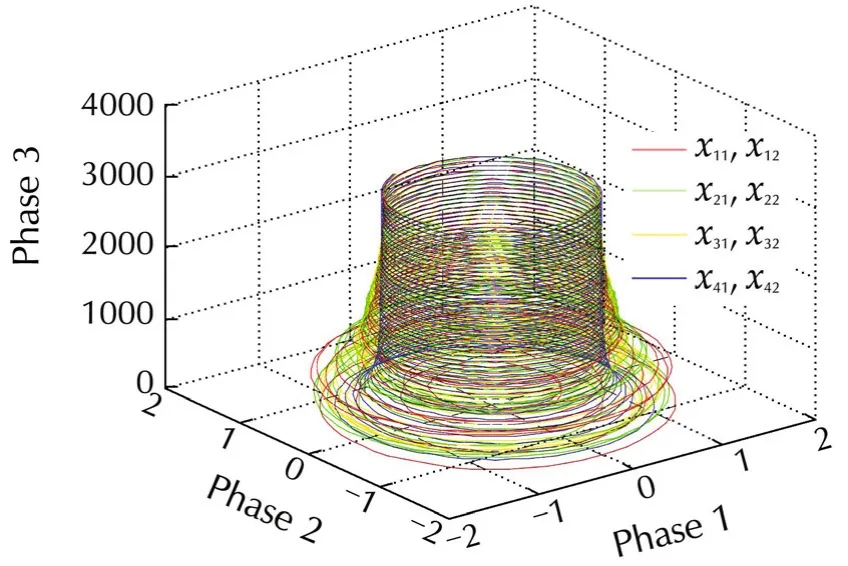
Fig.4 Phase plot of the agents.

7 Conclusions

This paper studies a class of discrete-time dynamical games known as dynamic graphical games.Novel coupled Bellman equations and Hamiltonian functions are developed to solve the graphical game.Optimal control solutions for the dynamic graphical game are given in terms of the solutions to a set of coupled DTHJB equations.The stability and Nash solutions for the dynamic graphical game are proved.An online model-free policy iteration algorithm is developed to solve the dynamic graphical game in real-time.The developed algorithm does not require the knowledge of any of the agents’dynamics.Policy iteration convergence proof for the dynamic graphical game is given.A gradient descent technique with critic network structures is used to implement the online policy iteration algorithm to solve the dynamic graphical game.

[1]P.J.Werbos.Neural networks for control and system identification.Proceedings of the 28th IEEE Conference on Decision and Control,New York:IEEE,1989:260–265.

[2]P.J.Werbos.Approximate Dynamic Programming for Real-time Control and Neural Modeling.Handbook of Intelligent Control.D.A.White,D.A.Sofge(ed.).New York:Van Nostrand Reinhold,1992.

[3]M.I.Abouheaf,F.L.Lewis,S.Haesaert,et al.Multi-agent discrete-time graphical games:interactive Nash equilibrium and value iteration solution.Proceedings of the American Control Conference,New York:IEEE,2013:4189–4195.

[4]K.G.Vamvoudakis,F.L.Lewis,G.R.Hudas.Multi-agent differential graphical games:online adaptive learning solution for synchronization with optimality.Automatica,2012,48(8):1598–1611.

[5]A.E.Bryson.Optimalcontrol-1950 to 1985.IEEE ControlSystems,1996,16(3):26–33.

[6]F.L.Lewis,D.Vrabie,V.L.Syrmos.Optimal Control.3rd ed.New York:John Wileyamp;Sons,2012.

[7]J.E.Marsden,M.West.Discrete mechanics and variational integrators.Acta Numerica,2001,10(5):357–514.

[8] Y.B.Suris.Discrete Lagrangian models.International School on Discrete Integrable Systems,Berlin:Springer,2004:111–184.

[9]S.Lall,M.West.Discrete variational Hamiltonian mechanics.Journal of Physics A:Mathematical and General,2006,39(19):5509–5519.

[10]S.Mu,T.Chu,L.Wang.Coordinated collective motion in a motile particle group with a leader.Physica A,2005,351(2/4):211–226.

[11]R.W.Beard,V.Stepanyan.Synchronization of information in distributed multiple vehicle coordinated control.Proceedings of the IEEE Conference on Decision and Control,Maui:IEEE,2003:2029–2034.

[12]A.Jadbabaie,J.Lin,A.Morse.Coordination of groups of mobile autonomous agents using nearest neighbor rules.IEEE Transactions on Automatic Control,2003,48(6):988–1001.

[13]R.Olfati-Saber,R.Murray.Consensus problems in networks of agents with switching topology and time-delays.IEEE Transactions on Automatic Control,2004,49(9):1520–1533.

[14]Z.Qu.Cooperative Control of Dynamical Systems:Applications to Autonomous Vehicles.New York:Springer,2009.

[15]W.Ren,R.Beard,E.Atkins.A survey of consensus problems in multi-agent coordination.Proceedings of the American Control Conference,New York:IEEE,2005:1859–1864.

[16]J.Tsitsiklis.Problems in Decentralized Decision Making and Computation.Ph.D.dissertation.Cambridge,MA:Department of Electrical Engineering and Computer Science,Massachusetts Institute of Technology,1984.

[17]Z.Li,Z.Duan,G.Chen,et al.Consensus of multi-agent systems and synchronization of complex networks:A unified viewpoint.IEEE Transactions on Circuits and Systems,2010,57(1):213–224.

[18]X.Li,X.Wang,G.Chen.Pinning a complex dynamical network to its equilibrium.IEEE Transactions on Circuits and Systems,2004,51(10):2074–2087.

[19]W.Ren,K.Moore,Y.Chen.High-order and model reference consensus algorithms in cooperative control of multivehicle systems.Journal of Dynamic Systems,Measurement and Control,2007,129(5):678–688.

[20]J.Kuang,J.Zhu.On consensus protocols for high-order multiagent systems.Journal of Control Theory and Applications,2010,8(4):406–412.

[21]S.Zhang,G.Duan.Consensusseeking in multi-agentcooperative control systems with bounded control input.Journal of Control Theory and Applications,2011,9(2):210–214.

[22]R.Gopalakrishnan,J.R.Marden,A.Wierman.An architectural view of game theoretic control.Performance Evaluation Review,2011,38(3):31–36.

[23]T.Ba¸sar,G.J.Olsder.Dynamic Non-cooperative Game Theory.Classics in Applied Mathematics.2nd ed.Philadelphia:SIAM,1999.

[24]G.Freiling,G.Jank,H.Abou-Kandil.On global existence of Solutions to coupled matrix Riccatiequations in closed-loop Nash Games.IEEE Transactions on Automatic Control,2002,41(2):264–269.

[25]Z.Gajic,T.-Y.Li.Simulation results for two new algorithms for solving coupled algebraic Riccati equations.Proceedings of the 3rd International Symposium on Differential Games.Sophia Antipolis,France,1988.

[26]A.G.Barto,R.S.Sutton,C.W.Anderson.Neuron like adaptive elements that can solve difficult learning control problems.IEEE Transactions on Systems Man and Cybernetics,1983,13(5):834–846.

[27]R.Howard.Dynamic Programming and Markov Processes.Cambridge,MA:MIT Press,1960.

[28]R.Bellman.DynamicProgramming.Princeton:Princeton University Press,1957.

[29]D.P.Bertsekas,J.N.Tsitsiklis.Neuro-dynamic Programming.Belmont,MA:Athena Scientific 1996.

[30]P.J.Werbos.Intelligence in the Brain:a theory of how it works and how to build it.Conference on Goal-Directed NeuralSystems,Oxford:Pergamon-Elsevier Science Ltd.,2009:200–212.

[31]D.Vrabie,F.L.Lewis.Adaptive dynamic programming for online solution ofa zero-sumdifferentialgame.JournalofControlTheory and Applications,2011,9(3):353–360.

[32]J.Morimoto,G.Zeglin,C.Atkeson.Minimax differential dynamic programming:application to a biped walking robot.IEEE/RSJ International Conference on Intelligent Robots and Systems,New York:IEEE,2003:1927–1932.

[33]T.Landelius.Reinforcement Learning and Distributed Local Model Synthesis.Ph.D.dissertation.Sweden:Linkoping University,1997.

[34]R.S.Sutton,A.G.Barto.Reinforcement Learning-An Introduction.Cambridge,MA:MIT Press,1998.

[35]S.Sen,G.Weiss.Learning In Multiagent Systems,in Multiagent Systems:A Modern Approach to Distributed Artificial Intelligence.Cambridge,MA:MIT Press,1999:259–298.

[36]K.G.Vamvoudakis,F.L.Lewis.Online actor-critic algorithm to solve the continuous-time infinite horizon optimal control problem.Automatica,2010,46(5):878–888.

[37]K.G.Vamvoudakis,F.L.Lewis.Multi-player non-zero sum games:online adaptive learning solution of coupled Hamilton-Jacobi equations.Automatica,2011,47(8):1556–1569.

[38]D.Vrabie,O.Pastravanu,F.L.Lewis,et al.Adaptive optimal control for continuous-time linear systems based on policy iteration.Automatica,2009,45(2):477–484.

[39]D.P.Bertsekas.Approximate policy iteration:A survey and some new methods.Journal of Control Theory and Applications,2011,9(3):310–335.

[40]L.Busoniu,R.Babuska,B.De-Schutter.A comprehensive survey of multiagent reinforcement learning.IEEE Transactions on Systems,Man and Cybernetics,2008,38(2):156–172.

[41]P.Vrancx,K.Verbeeck,A.Nowe.Decentralized learning in markov games.IEEE Transactions on Systems,Man and Cybernetics,2008,38(4):976–981.

[42]M.L.Littman.Value-function reinforcement learning in Markov games.Cognitive Systems Research,2001,2(1):55–66.

[43]Y.Jiang,Z.Jiang.Computational adaptive optimal control for continuous-time linear systems with completely unknown dynamics.Automatica,2012,48(10):2699–2704.

[44]Y.Jiang,Z.Jiang.Global adaptive dynamic programming for continuous-time nonlinear systems.2013:http://arxiv.org/abs/1401.0020.

[45]T.Dierks,S.Jagannathan.Optimal control of affine nonlinear continuous-time systems using an online Hamilton-Jacobi-Isaacs formulation.Proceedings of the 49th IEEE Conference on Decision and Control,New York:IEEE,2010:3048–3053.

[46]M.Johnson,T.Hiramatsu,N.Fitz-Coy,et al.Asymptotic Stackelberg optimal control design for an uncertain Euler Lagrange system.Proceedings of the 49th IEEE Conference on Decision and Control,New York:IEEE,2010:6686–6691.

[47]F.L.Lewis.Applied Optimal Control and Estimation:Digital Design and Implementation.Englewood Cliffs:Prentice Hall,1992.

[48]S.Khoo,L.Xie,Z.Man.Robust finite-time consensus tracking algorithm for multirobot systems.IEEE/ASME Transactions on Mechatronics,2009,14(2):219–228.

Mohammed I.ABOUHEAFwas born in Smanoud,Egypt.He received his B.Sc.and M.Sc.degrees in Electronics and Communication Engineering,Mansoura College of Engineering,Mansoura,Egypt,in 2000 and 2006,respectively.He worked as an assistant lecturer with the Air Defense College,Alexandria,Egypt(2001-2002).He worked as a planning engineer for the Maintenance Department,Suez Oil Company(SUCO),South Sinai,Egypt(2002-2004).He worked as an assistant lecturer with the Electrical Engineering Department,Aswan College of Energy Engineering,Aswan,Egypt(2004-2008).He received his Ph.D.degree in Electrical Engineering,University of Texas at Arlington(UTA),Arlington,Texas,U.S.A.in 2012.He worked as a postdoctoral fellow with the University of Texas at Arlington Research Institute(UTARI),Fort Worth,Texas,U.S.A.(2012-2013).He worked as Adjunct Faculty with the Electrical Engineering Department,University of Texas at Arlington(UTA),Arlington,Texas,U.S.A.(2012-2013).He was a member of the Advanced Controls and Sensor Group(ACS)and the Energy Systems Research Center(ESRC),University of Texas at Arlington,Arlington,Texas,U.S.A.(2008-2012).Currently,he is Assistant Professor with the Systems Engineering Department,King Fahd University of Petroleum and Minerals(KFUPM),Dhahran,Saudi Arabia.His research interests include optimal control,adaptive control,reinforcement learning,fuzzy systems,game theory,microgrids,and economic dispatch.E-mail:abouheaf@kfupm.edu.sa.

FrankL.LEWISis Member,National Academy of Inventors.Fellow IEEE,Fellow IFAC,Fellow,U.K.Institute of Measurementamp;Control,PE Texas,U.K.Chartered Engineer,UTA Distinguished Scholar Professor,UTA Distinguished Teaching Professor,and Moncrief-O’Donnell Chair at the University of Texas at Arlington Research Institute.He is Qian Ren Thousand Talents Consulting Professor,Northeastern University,Shenyang,China.He obtained the B.S.degree in Physics/EE and the MSEE at Rice University,the M.S.in Aeronautical Engineering from University of West Florida,and the Ph.D.degree at Georgia Institute of Technology.He works in feedback control,intelligent systems,cooperative control systems,and nonlinear systems.He is Author of 6 U.S.patents,numerous journal special issues,journal papers,and 20 books,including Optimal Control,Aircraft Control,Optimal Estimation,and Robot Manipulator Control which are used as university textbooks worldwide.He received the Fulbright Research Award,NSF Research Initiation Grant,ASEE Terman Award,Int.Neural Network Soc.Gabor Award,U.K.Inst Measurementamp;Control Honeywell Field Engineering Medal,and IEEE Computational Intelligence Society Neural Networks Pioneer Award.He received Outstanding Service Award from Dallas IEEE Section,and selected as Engineer of the year by Ft.Worth IEEE Section.He was listed in Ft.Worth Business Press Top 200 Leaders in Manufacturing.He received Texas Regents Outstanding Teaching Award 2013.He is Distinguished Visiting Professor at Nanjing University of Scienceamp;Technology and Project 111 Professor at Northeastern University in Shenyang,China.He is Founding Member of the Board of Governors of the Mediterranean Control Association.E-mail:lewis@uta.edu.

Magdi S.MAHMOUDobtained the B.Sc.degree(Honors)in Communication Engineering,M.Sc.degree in Electronic Engineering,and Ph.D.degree in Systems Engineering,all from Cairo University in 1968,1972 and 1974,respectively.He has been a professor of Engineering since 1984.He is now a distinguished professor at KFUPM,Saudi Arabia.He was on the faculty at different universities worldwide including Egypt(CU,AUC),Kuwait(KU),U.A.E.(UAEU),U.K.(UMIST),U.S.A.(Pitt,Case Western),Singapore(Nanyang)and Australia(Adelaide).He lectured in Venezuela(Caracas),Germany(Hanover),U.K.((Kent),U.S.A.(UoSA),Canada(Montreal)and China(BIT,Yanshan).He is the principalauthorofthirty-four(34)books,inclusive book-chapters and the author/co-author of more than 510 peer-reviewed papers.He is the recipient of two national,one regional and four university prizes for outstanding research in engineering and applied mathematics.He is a fellow of the IEE,a senior member of the IEEE,the CEI(U.K.),and a registered consultant engineer of information engineering and systems(Egypt).He is currently actively engaged in teaching and research in the development of modern methodologies to distributed control and filtering,networked-control systems,triggering mechanisms in dynamical systems,fault-tolerant systems and information technology.He is a fellow of the IEEE,a senior member of the IEEE,the CEI(U.K.),and a registered consultant engineer of information engineering and systems Egypt.E-mail:msmahmoud@kfupm.edu.sa,magdisadekmahmoud@gmail.com,magdim@yahoo.com.

Dariusz MIKULSKIis a research computer scientist in Ground Vehicle Robotics at the U.S.Army Tank-Automotive Research Development and Engineering Center in Warren,MI.He currently works on research to improve cooperative teaming and cyber security in military unmanned convoy operations.Dr.Mikulski earned his Ph.D.degree in Electrical and Computer Engineering at Oakland University in Rochester Hills,Michigan in 2013.He also earned his B.Sc.in Computer Science from the University of Michigan in Ann Arbor and Masters in Computer Science and Engineering from Oakland University.E-mail:dariusz.g.mikulski.civ@mail.mil.

†Corresponding author.

E-mail:abouheaf@kfupm.edu.sa.Tel.:+966(13)860 2968;fax:+966(13)860 2965.King Fahd University of Petroleumamp;Mineral,P.O.Box 1956,Dhahran-31261,Saudi Arabia.

This work was supported by the Deanship of Scientific Research at King Fahd University of Petroleumamp;Minerals Project(No.JF141002),the National Science Foundation(No.ECCS-1405173),the Office of Naval Research(Nos.N000141310562,N000141410718),the U.S.Army Research Office(No.W911NF-11-D-0001),the National Natural Science Foundation of China(No.61120106011),and the Project 111 from the Ministry of Education of China(No.B08015).

©2015 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg