Pinning synchronization of networked multi-agent systems:spectral analysis

Linying XIANG ,Fei CHEN ,Guanrong CHEN

1.Department of Automation,Xiamen University,Xiamen Fujian 361005,China;

2.Department of Electronic Engineering,City University of Hong Kong,Kowloon,Hong Kong,China

Received 10 March 2014;revised 20 September 2014;accepted 28 September 2014

Pinning synchronization of networked multi-agent systems:spectral analysis

Linying XIANG1,Fei CHEN1,Guanrong CHEN2†

1.Department of Automation,Xiamen University,Xiamen Fujian 361005,China;

2.Department of Electronic Engineering,City University of Hong Kong,Kowloon,Hong Kong,China

Received 10 March 2014;revised 20 September 2014;accepted 28 September 2014

Pinning synchronization of a networked multi-agent system with a directed communication topology is investigated from a spectral analysis approach.Some new types of synchronized regions for networked systems with different nonlinear agent dynamics and inner coupling structures are discovered.The eigenvalue distributions of the coupling and control matrices for different types of directed networks are obtained.The effects of the network topology,pinning density and pinning strength on the network synchronizability are examined through extensive numerical simulations.It is shown that the synchronizability of the pinned network can be effectively improved by increasing pinning density and pinning strength for some types of synchronized regions,whereas too large the pinning density and pinning strength will lead to desynchronization for other types.It is found that directed random networks are not always easier to synchronize than directed small-world networks,and a denser eigenvalue distribution may not always imply better synchronizability.

Multi-agent system,directed network,pinning control,spectral analysis,synchronizability,synchronized region

DOI 10.1007/s11768-015-4033-6

1 Introduction

Networked multi-agent system refers to dynamical system with multiple agents interconnected by a communication network.The last decade has witnessed a new arrival of interest and research in the study of consensus,synchronization,and control of networked multi-agent systems[1–5].This is partially due to the rapid development of communication and computation technologies,with wide applications of multi-agent systems in many areas including cooperative control of mobile robots,unmanned air vehicles,and autonomous formation flight.Therein,an important topic is determining the network synchronizability,i.e.,the width of the range of the global coupling strength needed to achieve network synchrony.In particular,the issueof enhancing the synchronizability of a complex networked system with two typical types of synchronized regions,namely unbounded and bounded regions,has stimulated broad interest[6–9].Notice that asymmetric interactions are ubiquitous in natural and technological networks,such as the WWW,airline networks,autonomous robot networks,etc.Additionally,the determination of synchronized regions(or consensus regions[4])not only attributes to the above-mentioned network topologies but also is due to the diversities of individual agent dynamics and inner-coupling functions.Although some work has been carried out for different structures of synchronized regions[10,11],the issue of synchronized regions of more general networks remains an important and interesting problem for study.Exploring generic synchronized regions and then investigating the synchronizability of networked multi-agent systems with various topologies will help develop a better integrated understanding of the interplay between the complexity of the network topology and the collective dynamics of the networked systems.

In the seminal work of Pecora and Carroll[12],an approach based on the master stability function(MSF)was proposed to study the synchronization ofdynamical networks on regularorrelatively simple network topologies.In addition,the spectral analysis approach was developed to analyze the stability of the synchronous states in coupled chaotic oscillator systems[13].Both approaches are represented in the complex plane and provide powerful frameworks to study the relationship between the structure and the synchronizability of a networked system.The weakest condition for all the Lyapunov exponents of the error dynamical system to be negative was suggested to guarantee the stability of the synchronous state,and moreover the critical curve of the synchronized region is determined by the largest Lyapunov exponent.Note that such a criterion assesses the stability of the completely synchronous state,which is necessary but not sufficient for synchronization.In particular,the network model considered in[13]is mainly determined by diffusive and gradient coupling coefficients;therefore,the underlying network can only be a regular or rather simple ones,of which the eigenvalues of the outer-coupling matrices can be calculated explicitly.However,for most real networked systems,the network structures are complex and irregular.Stimulated by this observation,there is growing interest in investigating the synchronization problem of more complicated networked systems and characterizing the structure-dynamics relationships.

From the application perspective,most realistic complex networked systems need external forces to function properly.For instance,when synchronization(or consensus)in a network of dynamical agents cannot be achieved through local interactions of the agents,or when the topology of a network is uncertain,external input to the networked system is necessary.In theory,it is possible to add control input to each agent,but this is usually not implementable due to physical constraints and high cost,particularly when the number of agents is very large.A sensible approach is to use pinning control to guide such a network of coupled dynamical systems onto a desired reference trajectory[14,15].It turns out that placing feedback controllers at a small portion of agents can indeed reduce the control cost dramatically and even improve controlperformances comparing with the strategy of controlling all or most of the agents[16–19].

Motivated by the above discussions,the spectralanalysis method is generalized here for pinning synchronization of multi-agent systems linked by directed networks.Different agent dynamics with chaotic behavior and different inner coupling matrices are considered.Accordingly,some new synchronized regions are discovered,and then some new indicators are given to evaluate the network synchronizability.It is found that for theU-shaped synchronized region of chaotic systems,the synchronizability of directed small-world networks with fixed in-degrees is better than directed random networks,which is in sharp contrast to some observations reported in the literature.It is also surprising to find that denser eigenvalue distribution does not always imply better synchronizability in networks withU,Λ,andM-shaped synchronized regions.

The rest of the paper is organized as follows.A new simple criterion for synchronization is given under the linear system theoretic framework in Section 2.The sign of the largest real part of the Jacobian eigenvalues,including the coupling and control terms,is used to characterize the shapes of the synchronized regions,and various essentially different structures of synchronized regions for arbitrary inner-couplings are identified in Section 3.In Section 4,the eigenvalue distributions of different outer-coupling and control matrices are investigated.The dependence of synchronizability on the network topology,pinning density,and pinning strength is discussed in detail based on spectral analysis and numerical simulation,with special emphasis on the newly found synchronized regions.Finally,Section 5 gives a few remarks as conclusion.

Throughoutthe paper,Rmdenotes them-dimensional Euclidean space and Rm×nthe set of all realm×nmatrices.Then×nidentity matrix is denoted byIn.The superscript“T”stands for matrix transpose and ⊗denotes the Kronecker product.Let diag{a1,...,an}be then×ndiagonal matrix with its diagonal elements beinga1,...,an.Let j denote the imaginary unit satisfying j2= −1 and|·|be the absolute value of a real number.Re(·)is the real part of a complex number and Im(·)its imaginary part.

2 Network stability from spectral analysis

Consider a multi-agent system consisting ofNagents described by

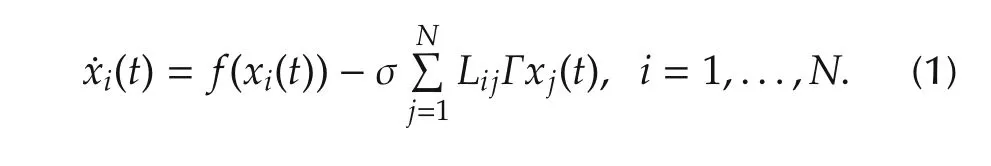
Here,xi∈Rmis the state vector of theith agent,and the nonlinear functionf(·)is continuously differentiable,capable of producing various rich dynamical behaviors.The realparameterσis a positive constantdescribing the global coupling strength.Γ ∈ Rm×mis a constant matrix representing the inner coupling of the agents.In this paper,it is assumed that each entry of the constant matrix Γ is either 0 or 1.The Laplacian matrixL=(Lij)∈ RN×Nsatisfying zero-row sum denotes the outer-coupling among the agents.The topological information on the directed network is encoded in matrixL,whose entriesLijare defined as follows:if there is a directed edge from agentjto agenti,thenLijlt;0;otherwise,Lij=0(j?i).

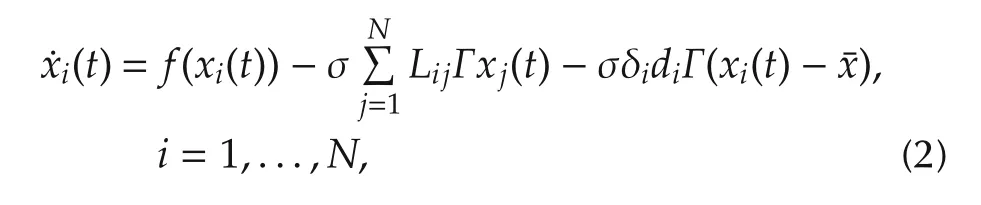
The matrixCcan be written asG=P−1CP,whereGis the Jordan canonical form ofCwhich is upper triangular.Introducing a transformation η(t)=(P−1⊗Im)E(t),along with the error system(3),yields

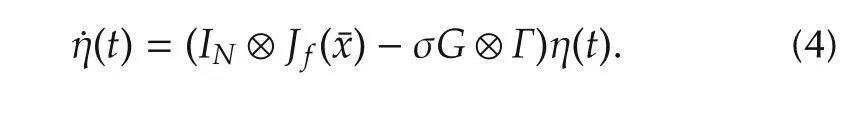
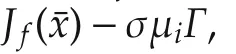
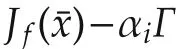
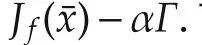
3 Synchronized regions for some typical chaotic systems

3.1 Nonlinear systems

Here,two representative nonlinear systems with chaotic behaviors are introduced.

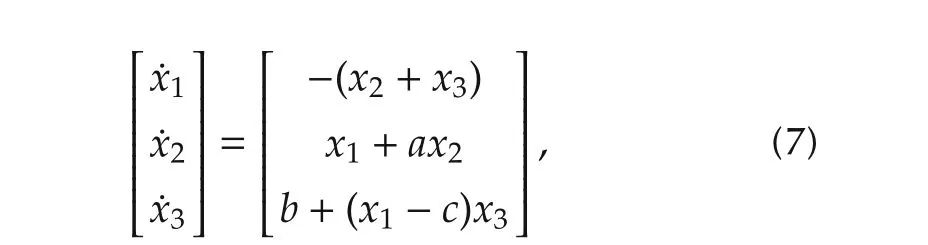
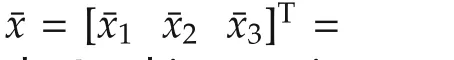
is given by

3.1.2 Chen system

A single Chen system[22]is described by

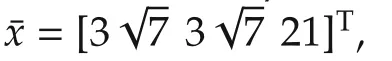
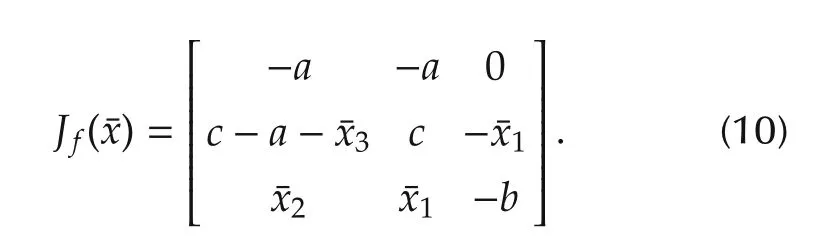
3.2 Generic parameter α is complex

Fig.1 Distributions of synchronized regions(“S”,dark grey shaded areas)of the synchronous state inset in Fig.1(h)shows the synchronized region for Re(λ)∈ [0,2].

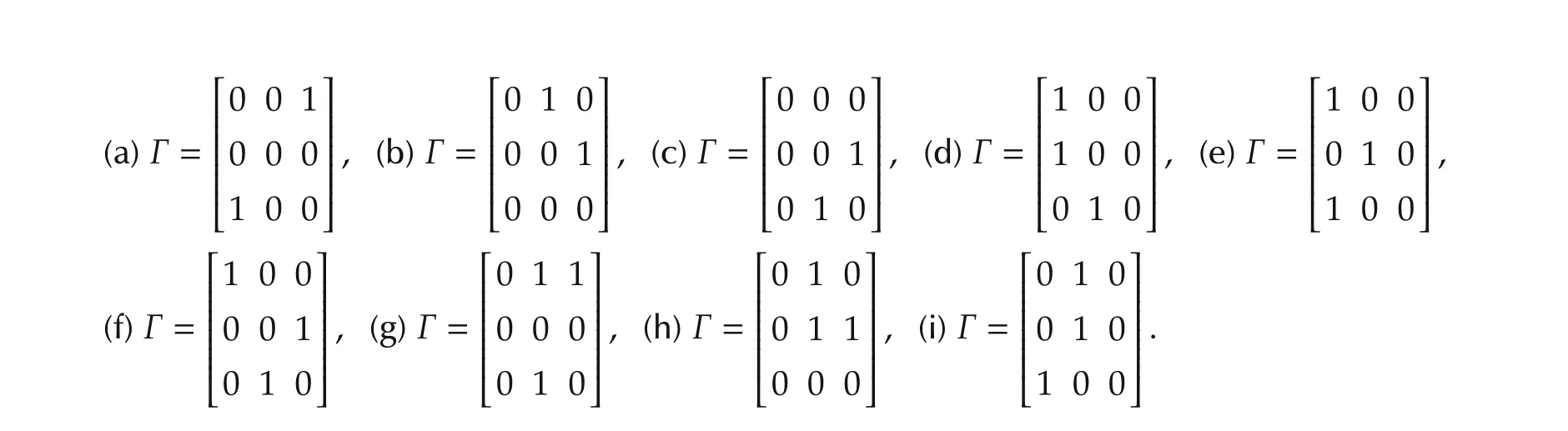
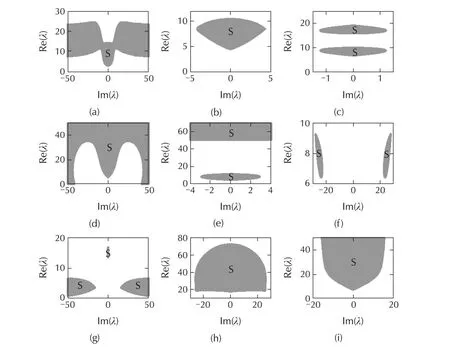
Fig.2 Distributions of synchronized regions(“S”,dark grey shaded areas)of the synchronous state¯x for the Chen system.

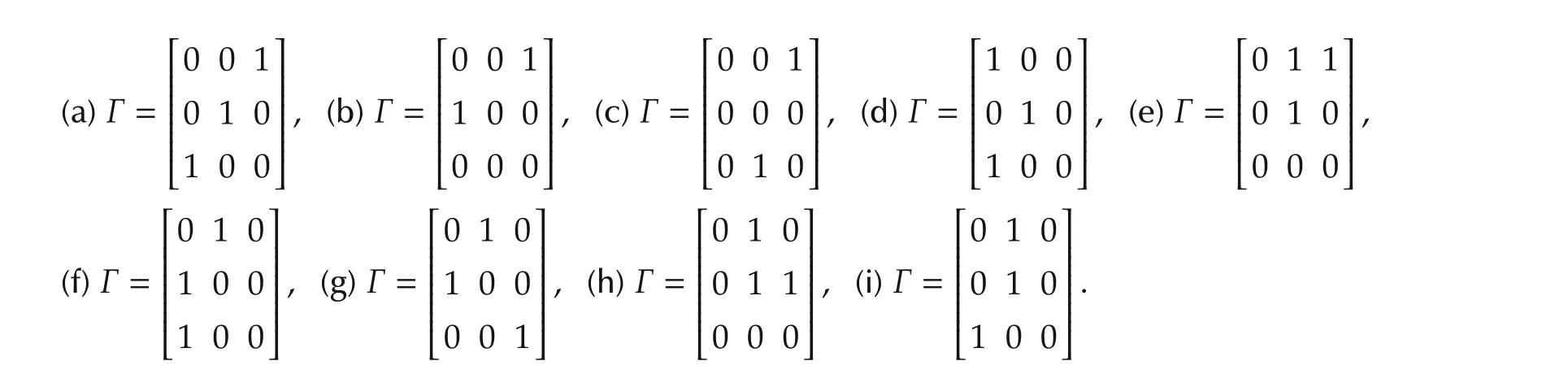
The intricate geometrical structures of synchronized regions in terms of critical boundaries shown in Figs.1 and 2 can be classified into the following classes.

Class i),shown in Figs.1(b),1(g),1(i),2(b),and 2(h):the synchronized region is encircled by a single closed critical curve,i.e.,it is localized in a finite Re(λ)− Im(λ)region.

Class ii),shown in Figs.1(a),2(c),and 2(f):the synchronized region is encircled by two closed critical curves.

Class iii),shown in Fig.2(i):the critical curve isU-shaped.Fig.1(d)is a kind of mixture of classes i)and iii).

Class iv),shown in Fig.1(e):the critical curve is Λ-shaped.

Class v),shown in Fig.2(d):the critical curve isM-shaped.Fig.2(a)is a kind of mixture of classes iii)and(v).

Class vi),shown in Fig.1(c):the critical curve forms two rough quarter-circles.Figs.1(f)and 2(g)can be seen as a kind of mixture of classes i)and vi).

Fig.2(e)is a kind of mixture of class i)and a stripe.Fig.1(h)is a kind of mixture ofVshape and a stripe.

4 Eigenvalue distributions

Regarding the above-mentioned synchronized regions,it is natural to ask:i)what are the synchronizabilities for different types of networked multi-agent systems?ii)what factors are key to the synchronizability?These two intrigued questions are to be answered subsequently.

To stabilize the synchronous state,the crucial issue is to move all the unstable eigenvalues(i.e.,eigenvalues in the desynchronized regions)ofLto the synchronized regions by designing a suitable control matrixD.In this section,various representative topologies of complex networks are considered.The effects of the structural characteristics of networks,pinning density,and pinning strength on the network synchronizability will be examined via extensive numerical tests.

First,starting with a regular ring network,where each nodeireceives directed edges from itskinearest neighbors.Here,the in-degreeki=k(kis chosen to be even)is the same for all nodes.Then,each outgoing edge is randomly cut with a probabilitypand is then rewired to a node chosen randomly from the whole network(avoiding multiple edges and self-loops).Note that an edge is allowed to be rewired back to its original position,and the in-degree of each node remains unchanged in the rewiring process.As the rewiring probabilitypis tuned from 0 to 1,the directed networks interpolate between regular ring networks(p=0),small worlds(lowp1),and completely random networks(p=1).This structural change induces changes in the corresponding graph’s Laplacian spectrum,and thus has a direct influence on the network synchronizability.

To examine how the rewiring probabilitypand the in-degreekaffect the synchronizability,the behaviors ofLfor various network sizesN∈{32,128,512,2048},by varyingpat fixedkand by varyingkat fixedp,are depicted in Figs.3 and 4,respectively.Note that the weights of the Laplacian matrices are fixed to 0 or 1 in Figs.3–5.In Fig.3,one increases the network sizeNbut keeps the in-degree of each node unchanged.It is observed that,the nonzero eigenvalues are uniformly distributed in an ellipse in the complex plane.It is interesting to see from Fig.3 that the whole ellipse is independent of the network sizeN,because largerNonly corresponds to denser distribution of eigenvalues inside the given ellipse.Furthermore,increasingpwill elongate the ellipse along the Im(λ)axisand willincrease the asymmetry ofthe totalcoupling.Note thatimaginary eigenvalues arise from asymmetric couplings.The larger the imaginary eigenvalue is,the stronger the asymmetry of the coupling will be.In Fig.4,when increasingN,the connection probabilitypis kept to be constant 1 whereask∈{2,4,6,10}.It can be seen that,for a large directed random network,the distribution of the nonzero eigenvalues forms an ellipse,and the radius of the ellipse shrinks askdecreases.This implies that the smaller the in-degree per node,the denser the eigenvalue distribution.In addition,the real parts of the nonzero eigenvalues increase askincreases.

In Fig.5,the eigenvalue distributions of σLare presented for those synchronized regions shown in Figs.1(e),1(h),2(d),and 2(i),respectively.It is surprising to see that the synchronizability of directed smallworld networks is better than random networks for theU-shaped synchronized region(see Fig.5(d)),which is different from the cases of classes iv),v)(see Figs.5(a)and 5(c),respectively),and the mixed structure shown in Fig.5(b).This suggests that random networks are not always more easily synchronized than small-world networks.It can be predicted from Fig.4 that,for directed random networks,the synchronizability is improved by increasing the in-degreek,for the synchronized regions shown in Fig.5.

Up to this point,the relevant factors on synchronizability such aspandkhave been discussed.In what follows,the focus is on the effects of both pinning density and pinning strength on the network synchronizability,which is a central issue related to network control.Here,it is assumed that all the nodes have normalized input strengths,i.e.,all the diagonal elementsLii≡ 1,∀i.The matrix is usually called the normalized Laplacian of that graph.

Fig.3 Eigenvalue distribution of L at fixed in-degree k=4.Mauve dots:p=0(purely real due to the initial ring symmetry).Blue dots:p=0.1.Red dots:p=0.4.Green dots:p=1.(a)N=32.(b)N=128.(c)N=512.(d)N=2048.

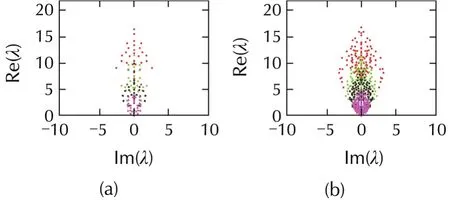
Fig.4 Eigenvalue distribution of L at fixed p=1.Mauve dots:k=2.Black dots:k=4.Green dots:k=6.Red dots:k=10.(a)N=32.(b)N=128.(c)N=512.(d)N=2048.

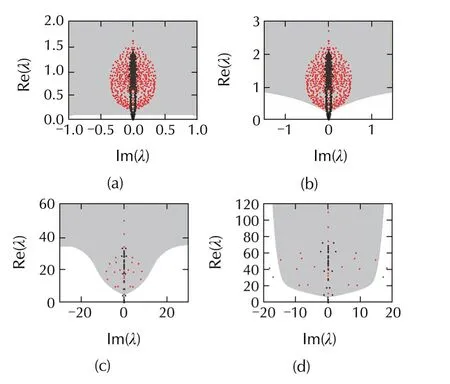
Fig.5 Eigenvalue distribution of σL at fixed in-degree k=4.Black dots:p=0.1.Red dots:p=1.(a)N=512,σ=0.2(the synchronized region in Fig.1(e)is considered).(b)N=512,σ=0.3(the synchronized region in Fig.1(h)is considered).(c)N=32,σ=5(the synchronized region in Fig.2(d)is considered).(d)N=32,σ=11(the synchronized region in Fig.2(i)is considered).

In Fig.6,various eigenvalue distributions ofthe matrix σCfor differentlanddare plotted.The synchronized region in Fig.1(f)is considered.Black dots represent the eigenvalues of σCwithout control,while red dots represent the eigenvalues of σCunder control,where a directed small-world network with in-degreek=2 andp=0.8 is considered.These notations are also used for Figs.7–9.Recall that there are five eigenvalues(black dots)staying in the desynchronized region without control.Settingl=16 andd=0.73,all the eigenvalues(red dots)eventually fall into the synchronized region,as seen in Fig.6(a).Keep all the parameters fixed in Fig.6(a),except increasing the pinning strength tod=0.85.An interesting phenomenon occurs:the top four eigenvalues first cross the upper critical curve and enter the desynchronized region,thus the network fails to synchronize.Continuously increasing the pinning density tol=20 in Fig.6(a),the same phenomenon in Fig.6(b)is also observed.This implies that too strong the pinning density and/or pinning strength will suppress synchronization in networks with bounded stable regions like Fig.1(f).Namely,there exist regions(lmin,lmax)and(dmin,dmax),respectively,among which pinning synchronization can be wellrealized.Itcan be deduced that,to achieve synchronization in the structures of class i)and mixture structures in Fig.2(a)(see Fig.7),pinning control is necessary to obtain similar results.

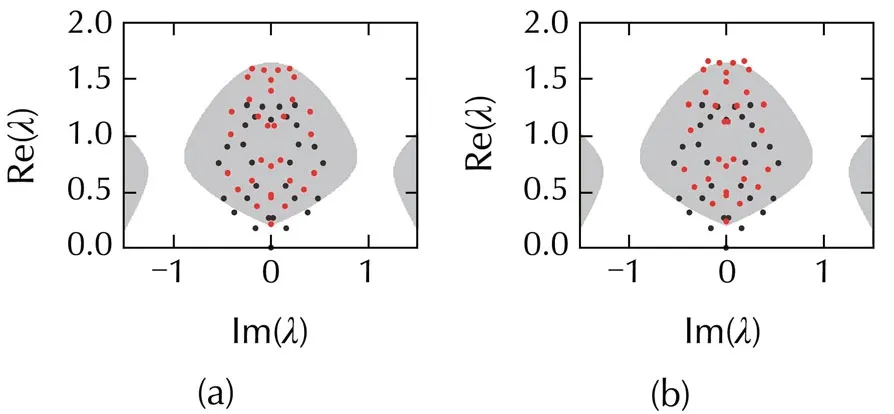
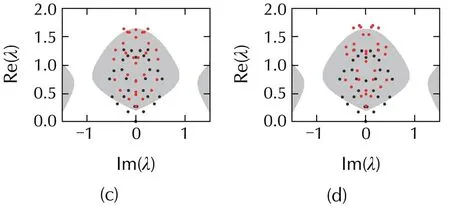
Fig.6 Eigenvalue distribution of the matrix σC(the synchronized region in Fig.1(f)is considered).Black dots denote the eigenvalues of σC without control,while red dots those under control.N=32,σ=0.72,k=2,and p=0.8.(a)l=16,d=0.73.(b)l=16,d=0.85.(c)l=20,d=0.73.(d)l=21,d=0.8.

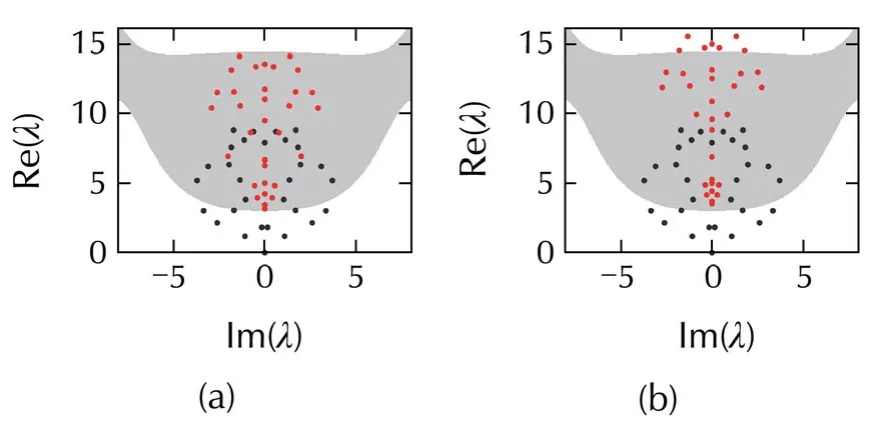
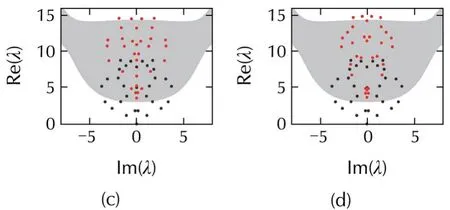
Fig.7 Eigenvalue distribution of the matrix σC(the synchronized region in Fig.2(a)is considered).Notations as Fig.6.N=32,σ=5,k=2,and p=0.8.(a)l=22,d=1.2.(b)l=22,d=1.5.(c)l=26,d=1.2.(d)l=25,d=1.3.

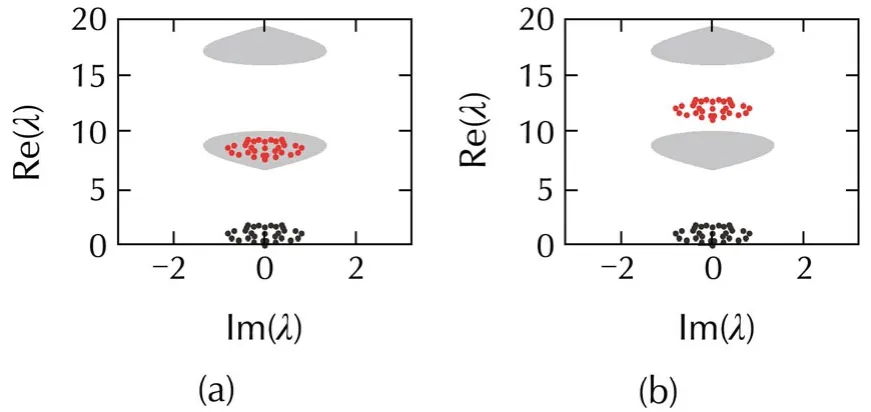
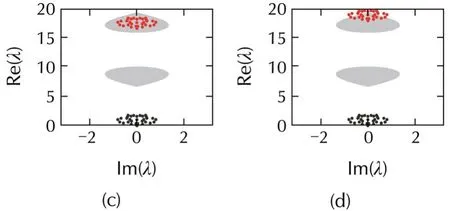
Fig.8 Eigenvalue distribution of the matrix σC(the synchronized region in Fig.2(c)is considered).Notations as Fig.6.N=32,σ=1,k=2,and p=0.8.(a)l=32,d=7.5.(b)l=32,d=11.(c)l=32,d=16.5.(d)l=32,d=17.8.

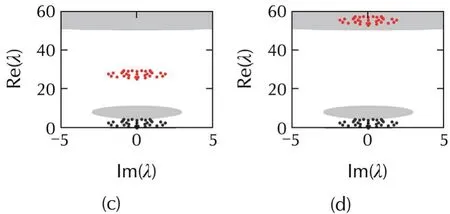
Fig.9 Eigenvalue distribution of the matrix σC(the synchronized region in Fig.2(e)is considered).Notations as Fig.6.N=32,σ=2.5,k=2,and p=0.8.(a)l=32,d=2.3.(b)l=32,d=3.5.(c)l=32,d=10.(d)l=32,d=21.

In Fig.8,the case of Fig.2(c)is considered.It is evident that the area of the bounded synchronized region is very small,and thus all the nodes should be pinned to achieve synchronization.Settingl=32 andd=7.5,all the eigenvalues fall into the first closed synchronized region,thus pinning synchronization is naturally achieved,as shown in Fig.8(a).Further increasing the pinning strength untild=11,as shown in Fig.8(b),reveals that all the eigenvalues cross the first bottom critical curve and move into the desynchronized region,so the pinned network becomes desynchronizable.As can be seen from Fig.8(c),successively increasing the pinning strengthdin Fig.8(b)makes all the eigenvalues move up,but they are located inside the second closed synchronized region.Itis apparentthatthe eigenvalues move up to the desynchronized region once again with the increase ofd(see Fig.8(d)).Therefore,one can conclude that there exist two regions,(d1min,d1max)and(d2min,d2max),among which pinning synchronization can be well realized in the case of Fig.2(c).Furthermore,one can deduce that the reasonable intervals ofdforguaranteeing the synchronization stability are(d1min,d1max)and(d2min,+∞),as shown in Fig.9.

5 Conclusions

A generalized spectral analysis approach to studying networked multi-agentsystems with directed topologies subjected to pinning control has been presented.Under the new formalism,the stability of the completely synchronous state is converted to two sub-problems.The first sub-problem is to identify the synchronized regions in the complex plane,where the modified error dynamical system admits eigenvalues with a negative largest real part.The second sub-problem is to verify whether the eigenvalues of an associated matrix lie in the synchronized regions.The two sub-problems are independent of each other,because the former depends solely on the individual agent dynamics and the innercoupling while the latter depends only on the interactions among the agents and the control mechanism.It should be emphasized that identifying the shapes of the synchronized regions of the given agent dynamics and the inner-coupling links is the prerequisite to investigate several important issues related to synchronization and control of networked multi-agent systems.

In this paper,although numerical simulations are performed with two chaotic systems on complex networks of typical topologies,the extension to other general systems and to other network structures is possible.The interesting results of the present paper give some clues about the concurrent relationship between the topological and the dynamical features of complex networked systems,for example the formation of social collective behaviors such as opinions,news,fashion,rumors,and political orientations.

Future research along the same line could study the settings with noise,uncertainties,time delays,timevarying topologies,and so on.In addition,some relevant problems of complex networks with nonidentical agent dynamics are challenging but worthy of future investigation.The concept of“cluster synchronization”[23,24]may also build up a general framework for future research on similar topics.

[1]W.Ren,R.W.Beard.Consensus seeking in multiagent systems under dynamically changing interaction topologies.IEEE Transactions on Automatic Control,2005,50(5):655–661.

[2]F.Chen,Y.Cao,W.Ren.Distributed average tracking of multiple time-varying reference signals with bounded derivatives.IEEE Transactions on Automatic Control,2012,57(12):3169–3174.

[3]W.Yu,G.Chen,J.L¨u,et al.Synchronization via pinning control on general complex networks.SIAM Journal on Control and Optimization,2013,51(2):1395–1416.

[4]Z.Li,Z.Duan,G.Chen,et al.Consensus of multiagent systems and synchronization of complex networks:a unified viewpoint.IEEE Transactions on Circuits and Systems–I,2010,57(1):213–224.

[5] Z.Li,X.Liu,W.Ren,et al.Distributed tracking control for linear multi-agent systems with a leader of bounded unknown input.IEEE Transactions on Automatic Control,2013,58(2):518–523.

[6]M.Barahona,L.M.Pecora.Synchronization in small-world systems.Physical Review Letters,2002,89(5):DOI 10.1103/PhysRevLett.89.054101.

[7] C.Zhou,A.E.Motter,J.Kurths.Universality in the synchronization of weighted random networks.Physical Review Letters,2006,96(3):DOI 10.1103/PhysRevLett.96.034101.

[8]G.Chen,Z.Duan.Network synchronizability analysis:a graph-theoretic approach.Chaos,2008,18(3):DOI 10.1063/1.2965530.

[9]D.Shi,G.Chen,W.W.K.Thong,et al.Searching for optimal network topology with best possible synchronizability.IEEE Circuits and Systems Magazine,2013,13(1):66–75.

[10]A.Stefa´nski,P.Perlikowski,T.Kapitaniak.Ragged synchronizability of coupled oscillators.Physical Review E,2007,75(1):DOI 10.1103/PhysRevE.75.016210.

[11]Z.Duan,G.Chen,L.Huang.Synchronization of weighted networks and complex synchronized regions.Physics Letters A,2008,372(21):3741–3751.

[12]L.M.Pecora,T.L.Carroll.Master stability functions for synchronized coupled systems.Physical Review Letters,1998,80(10):2109–2112.

[13]G.Hu,J.Yang,W.Liu.Instability and controllability of linearly coupled oscillators:eigenvalue analysis.Physical Review E,1998,58(4):4440–4453.

[14]X.Wang,G.Chen.Pinning control of scale-free dynamical networks.Physica A,2002,310(3):521–531.

[15]X.Li,X.Wang,G.Chen.Pinning a complex dynamical network to its equilibrium.IEEE Transactions on Circuits and Systems–I,2004,51(10):2074–2087.

[16]J.Xiang,G.Chen.On theV-stability of complex dynamical networks.Automatica,2007,43(6):1049–1057.

[17]L.Xiang,Z.Liu,Z.Chen,et al.Pinning control of complex dynamical networks with general topology.Physica A,2007,379(1):298–306.

[18]M.Porfiri,M.di Bernardo.Criteria for global pinningcontrollability of complex networks.Automatica,2008,44(12):3100–3106.

[19]F.Chen,Z.Chen,L.Xiang,etal.Reaching a consensus via pinning control.Automatica,2009,45(5):1215–1220.

[20]C.W.Wu,L.O.Chua.Application of Kronecker products to the analysis of systems with uniform linear coupling.IEEE Transactions on Circuits and Systems–I,1995,42(10):775–778.

[21]O.E.R¨ossler.An equation for continuous chaos.Physics Letters A,1976,57(5):397–398.

[22]G.Chen,T.Ueta.Yet another chaotic attractor.International Journal of Bifurcation and Chaos,1999,9(7):1465–1466.

[23]K.Wang,X.Fu,K.Li.Cluster synchronization in community networks with nonidentical nodes.Chaos,2009,19(2):DOI 10.1063/1.3125714.

[24]W.Qin,G.Chen.Coupling schemes for cluster synchronization in coupled Josephson equations.Physica D,2004,197(3/4):375–391.

her Ph.D.degree in Control Theory and Control Engineering from Nankai University,Tianjin,China,in 2008.From November 2008 to October 2010,she was a Postdoctoral Research Fellow at the City University of Hong Kong.From March 2013 to June 2013,she was a Senior Research Assistant with the Department of Electronic Engineering,City University of Hong Kong,Hong Kong.Since November 2010,she has been with the Department of Automation,Xiamen University,Xiamen,China,where she is currently an Associate Professor.Dr.Xiang was a Program Committee Member of Asian Control Conference and Chinese Conference of Complex Networks.Dr.Xiang’s research interests are in the area of synchronization and control of complex networks,coordinated control of multi-agent systems.E-mail:xiangly@xmu.edu.cn.

Fei CHENreceived his Ph.D.degree in Control Theory and Control Engineering from Nankai University,Tianjin,China,in 2009.From October2008 to January 2009,he was a Research Assistant with the Department of Electronic Engineering,City University of Hong Kong,Hong Kong.From August 2009 to August 2010,he was a Postdoctoral Researcher in the Department of Computer and Electrical Engineering,Utah State University,Logan,UT.From March 2013 to June 2013,he was a Senior Research Associate with the Department of Mechanical and Biomedical Engineering,City University of Hong Kong,Hong Kong.Since November 2010,he has been with the Department of Automation,Xiamen University,Xiamen,China,where he is currently an Associate Professor.Dr.Chen was a Program Committee Member of Asian Control Conference and Chinese Conference of Complex Networks.He was a recipient of the Award for New Century Excellent Talents in Fujian Province University and a recipient of the Distinguished Ph.D.Dissertation Award from Nankai University.Dr.Chen’s research interests are in the area of systems and control,multi-agent networks,and non-smooth analysis.E-mail:feichen@xmu.edu.cn.

Guanrong CHENhas been a Chair Professor and the Director of the Centre for Chaos and Complex Networks at the City University of Hong Kong since year 2000,prior to which he was a Tenured Full Professor at the University of Houston,Texas,USA.He was elected IEEE Fellow in 1997,awarded the 2011 EulerGold Medal,Russia,and conferred Honorary Doctorate by the Saint Petersburg State University,Russia in 2011 and by the University of Le Havre,France in 2014.He is a member of the Academia Europaea.E-mail:eegchen@cityu.edu.hk.

†Corresponding author.

E-mail:eegchen@cityu.edu.hk.

This work wassupported by the NationalNaturalScience Foundation ofChina(Nos.61104151,61104018,61473240),the Science Foundation of Fujian Province(No.2012J01289),and the Hong Kong Research Grants Council under the GRF Grant CityU 1120/14.

©2015 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg