Immersion and invariance adaptive control of a class of continuous stirred tank reactors

Gaiyan HONG ,Xiangbin LIU †,Hongye SU

1.School of Electronic Information Engineering,Beijing Jiaotong University,Beijing 100044,China;

2.Institute of Cyber-System and Control,Zhejiang University,Hangzhou Zhejiang 310027,China

Received 31 July 2014;revised 22 January 2015;accepted 22 January 2015

Immersion and invariance adaptive control of a class of continuous stirred tank reactors

Gaiyan HONG1,Xiangbin LIU1†,Hongye SU2

1.School of Electronic Information Engineering,Beijing Jiaotong University,Beijing 100044,China;

2.Institute of Cyber-System and Control,Zhejiang University,Hangzhou Zhejiang 310027,China

Received 31 July 2014;revised 22 January 2015;accepted 22 January 2015

An immersion and invariance(Iamp;I)manifold based adaptive control algorithm is presented for a class of continuous stirred tank reactors(CSTR)to realize performance-oriented control in this paper.The nonlinear contraction method is combined into the control law design to render the closed-loop CSTR system globally asymptotically stable,firstly.Then,the Iamp;I method is used to form the adaptation law such that the off-the-manifold coordinate(the parameter estimation error)converges to zero usingP-monotone property enforced by selecting tuning function in manifold.As a result,the state of the closed-loop CSTR converges to its desired value asymptotically.The simulation is given to illustrate the effectiveness of the presented algorithm.

CSTR,adaptive control,Iamp;I,nonlinearly parameterized uncertainty

DOI 10.1007/s11768-015-4111-9

1 Introduction

The continuous stirred tank reactor(CSTR)is a crucial device in chemical process,which is widely used in chemical,petroleum production,bio-pharmaceutical and other industrial production processes due to its good heat exchange capacity and stable product quality.On the other hand,CSTR shows strong nonlinearity,such as multi-equilibrium points and inputconstraint[1]and is easily affected by the otheruncertain factors,such as external conditions,concentrations of the raw materials,catalyst,the coolant temperature,flow change and so on in reaction process as well,which result in that the model of CSTR is a complicated and nonlinear uncertain model.

Due to its importance in process industry,there are many research results on the controller design of CSTR.In[2],the satisfying performances of the process can be obtained by the conventional PID controller as control input in reaction varies in small range.However,the desired control performance cannot be guaranteed by above PID controller due to its strong nonlinear charac-teristics to large range control input.In[1,3,4],several adaptive controllers have been presented to diminish the tracking error convergence when CSTR is operated for long periods of time in a neighborhood of one operating point.Due to the slow convergence of parameter estimation,the system may not have the desired transient performance.In[5],a robust control scheme was proposed to stabilize the temperature at any arbitrary set point despite of uncertainties on the kinetics.The final tracking is not satisfying since it does not differentiate between parametric uncertainty and uncertain nonlinearities in the control law.Using backstepping technique,a robust adaptive nonlinear controller for a benchmark CSTR was developed that is used to regulate the concentration of products[6].Asymptotic output tracking can be obtained by the adaptive backstepping and neural network controller in[7,8].In[1],an adaptive fuzzy logic algorithm is used to estimate the concentration dependent terms and other unknown system parameters appearing in control law.

In[9],a semi-adaptive state feedback controllerwhere adaptation only takes place in the region of the state space where convexity can be used to reduce parameter uncertainty is applied to the CSTR system.In the remaining part of the state space the controller would freeze the adaptation law and switch to a robust controller.This scheme ensures semi-global stability for convexly parameterized nonlinear systems with matched uncertainty.

Recently,a new methodology to design direct and indirect adaptive controllers for nonlinear systems,called Immersion and Invariance(Iamp;I)adaptive,has been proposed in[10].The control performance can be guaranteed by utilizing the properties of immersion and invariant manifold,which is realized by adding suitable tuning function to globally render the estimation error between the true value of the unknown parameters and its estimate converge to zero gradually.In fact,Iamp;I adaptive control can be applied for a general class of parameterized systems by selecting the tuning function to shape the converging dynamic of the parameter estimation error.In[11],a framework to design Iamp;I adaptive controllers for nonlinearly parameterized systems was proposed,which relies on a monotonic property enforced by the designer in the whole state space.

On the other hand,the way to construct the base-line controller for Iamp;I adaptive control,which renders the closed-loop system globally asymptotically stable(GAS),is not provided systematically.Thanks to the seminal papers[12,13],a nonlinear contraction method is presented to design GAS controller for nonlinear systems,which makes the way to constructthe Iamp;Ibased adaptive controller for nonlinearly parameterized systems completeness.

Due to the nonlinearly parameterize uncertainties in CSTR,an Iamp;Ibased adaptive controlcombined with nonlinear contraction method is presented to realize performance oriented control in this paper.The main motivation of the presented methods is to avoid the intricacies of Lyapunov function generation.The overall system is viewed as the cascade of a convergent estimator and a disturbed control system.The base-line controller using nonlinear contraction method is designed to make the closed-loop system stable provided knowing the true value of the unknown parameters.The Iamp;I adaptation law is constructed to recover unknown parameters such that the perturbation terms due to estimation error converge to zero monotonically,which results in the whole system globally asymptotically stable at desired state.

The rest of the paper is organized as follows:In Section 2,the dynamic model of CSTR considered is given.Section 3 presents the Iamp;I adaptive controller algorithm for the class of CSTR.The simulation is given to illustrate the effectiveness of the proposed controller in Section 4.The paper is wrapped up with some concluding remarks in Section 5.

2 Dynamic model of the considering CSTR

2.1 The model of the CSTR

The CSTR system consists of a constant volume reactor cooled by a single coolant stream flowing in a concurrentfashion.An irreversible,exothermic reaction,A→B,occurs in the tank.

The dynamic of the process of CSTR considered in this paper can be written in the following form[9]:

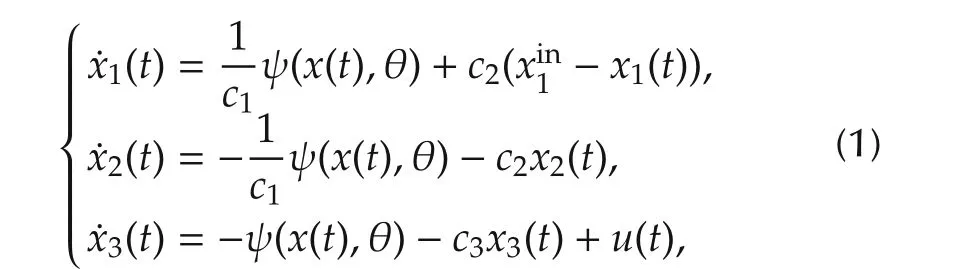
wherex(t)=[x1(t)x2(t)x3(t)]Tis the system state,x1(t),x2(t)denote the concentrations of materialAandB,respectively,u(t)the temperature in the tank of the reactor,xi1nis the constant feed concentration of materialA,andu(t)is the only manipulated variable which provides operating heat for CSTR.The kinetics function of the reactor−ψ(x(t),θ)=c1x1(t)eθ1e−(θ2/x3(t))satisfies Arrhenius law.c1,c2andc3are certain known positive constants;θ1and θ2are unknown parameters of kinetics function in CSTR,respectively,which are nonlinearly parameterized in kinetics function in nature.

To simplify the system expression in(1),the CSTR dynamic can be rewritten as

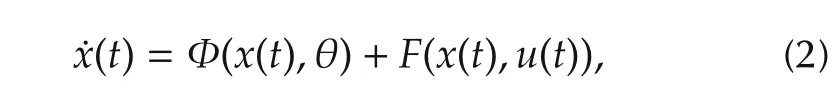
whereF(x(t),u(t))=[0 0u(t)]Tand

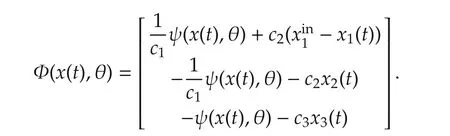
The control objective in this paper is to design the control law to the manipulated variableu(t)to regulate the temperaturex3(t)in(2)to desired valuex∗3such that the material concentrationsAandB,i.e.,x1(t)andx2(t)go to the desired statesx∗1(t)andx∗2(t).

3 Controller design

In this chapter,the Iamp;I based adaptive control is designed for the class of uncertain CSTR system(1).The controller design follows the procedure of Iamp;I adaptive controllerin[11]since the class ofCSTRs are nonlinearly parameterized uncertain systems.

Assumption1There exists a functionφ :Rn×Rq→R,such that the system

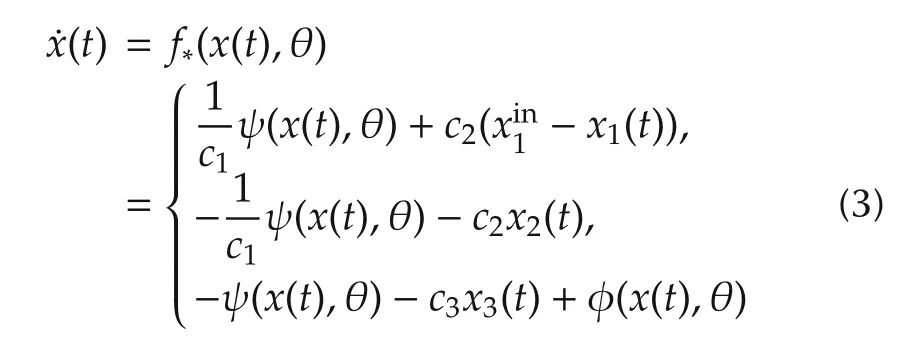
has a globally asymptotically stable equilibrium atx∗(t).

Remark1The design ofthe GAS controllersfornonlinear system is a hard work.Thanks to the seminal works[12,13]for nonlinear contraction method,they provide an systematic way to design GAS controller for nonlinear systems.

The following definitions are used in GAS controller design using nonlinear contraction.

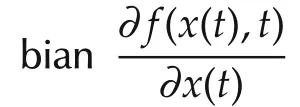
Lemma 1Given the system˙x(t)=f(x(t),t),any trajectory which starts in a ball of constant radius centered about a given trajectory and contained at all times in a contraction region,remains in that ball and converges exponentially to the given trajectory.Further,global exponential convergence is guaranteed if the whole state space region is contracting.

Proposition1Considering the CSTR(1),the control law

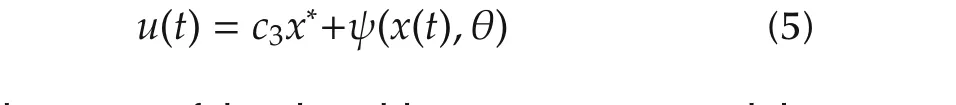
renders the states of the closed-loop CSTR system globally asymptotically converge to its desired statex∗.

ProofSubstituting(5)into(1),the closed-loop system is given as follows:

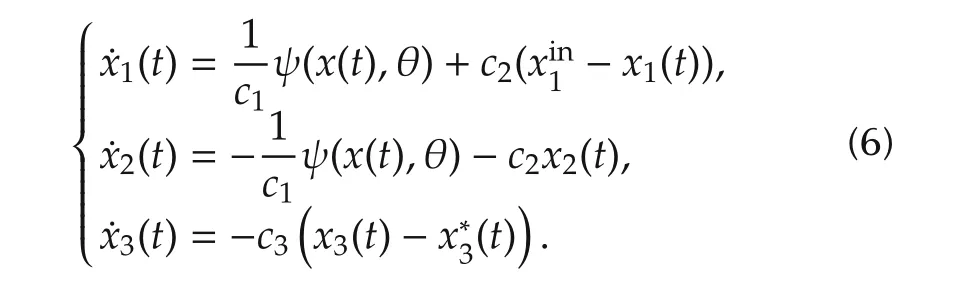
The derivative of variations of the state of(6)is calculated as

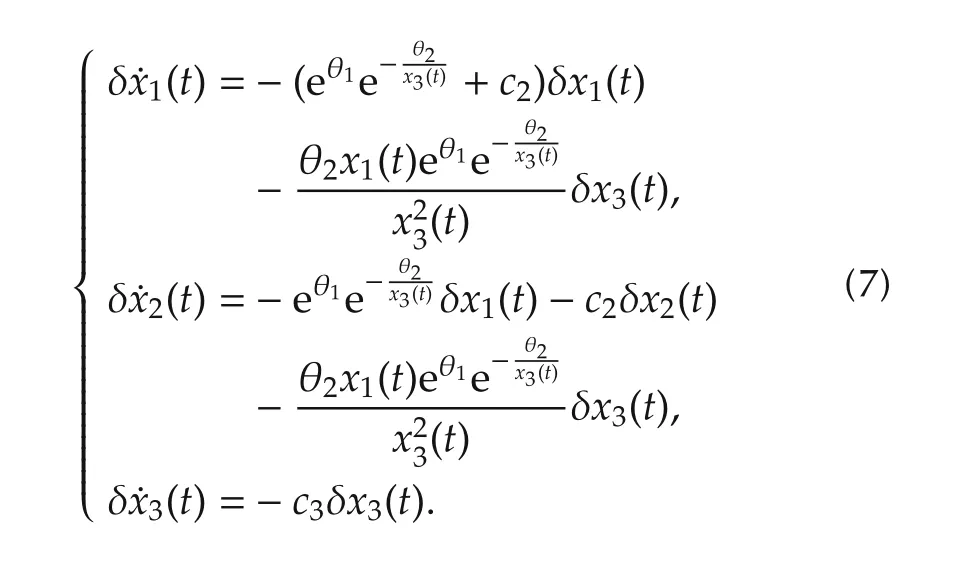
It is easy to verify that system(7)is uniformly negative definition forx(t)∈R3,which implies that the control law renders the CSTR globally asymptotical stable according to Theorem 1 in[12].

Since θ is unknown parameter vector in ψ(x(t),θ),the adaptation law must be adopted to recover θ.According to the controlobjective ofthe CSTR,the adaptive control for the uncertain CSTR is designed as follows:

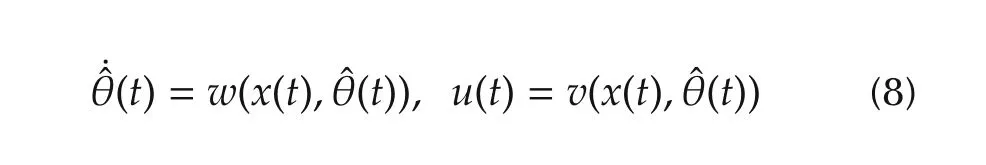
In[11],a framework of Iamp;I based adaptive control of nonlinearly parameterized systems including direct and indirect ways is proposed.In this paper,the direct version of Iamp;I adaptive control is used to realize the control of the class of CSTR.There is a differentiable function which is added to the estimated parameter vector,and the corresponding adaptive control for(8)is given as follows:

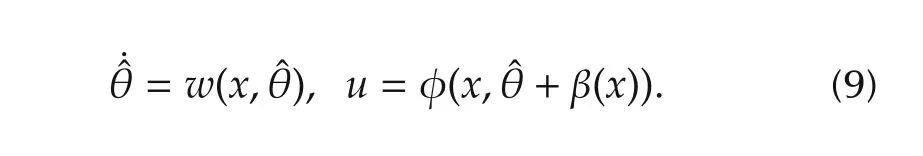
To specify the tuning function for the control objective,P-monotone definition is used in Iamp;Ibased adaptive control.

Def i nition 3(P-monotone)[11]Given a symmetric matrixP:Rq×qgt;0,a mappingL:Rq→ RqisP-monotone[resp.,strictlyP-monotone],if and only if

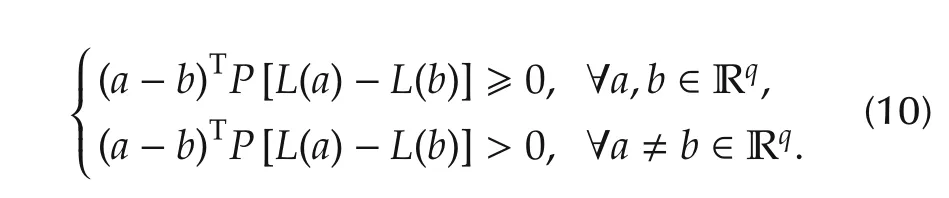
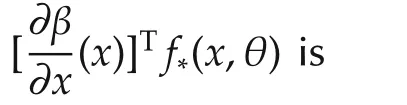
Remark2Assumption 2 iseasy verified forthe CSTR by direct calculation,which is the key requirement related to the class of CSTR to use direct Iamp;I adaptive control.

Assumption 3The parameterized mappingQxD(θ):Rq→Rq,

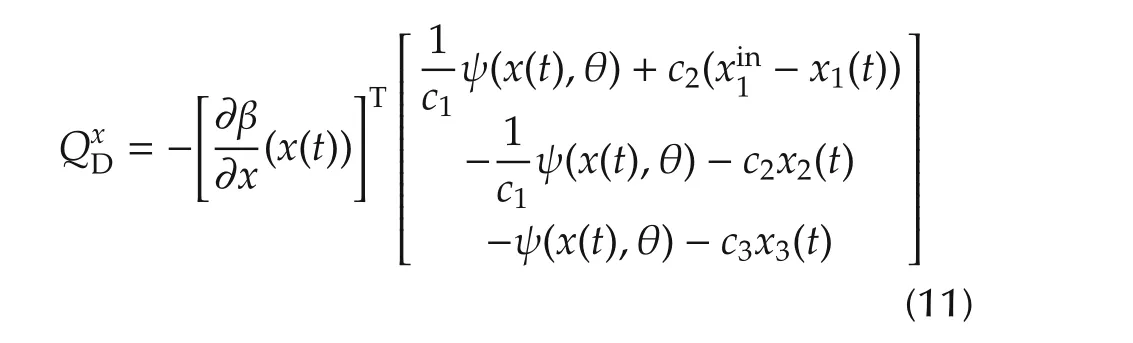
is strictlyP-monotone for allx∈Rn.

Assumption 4The system

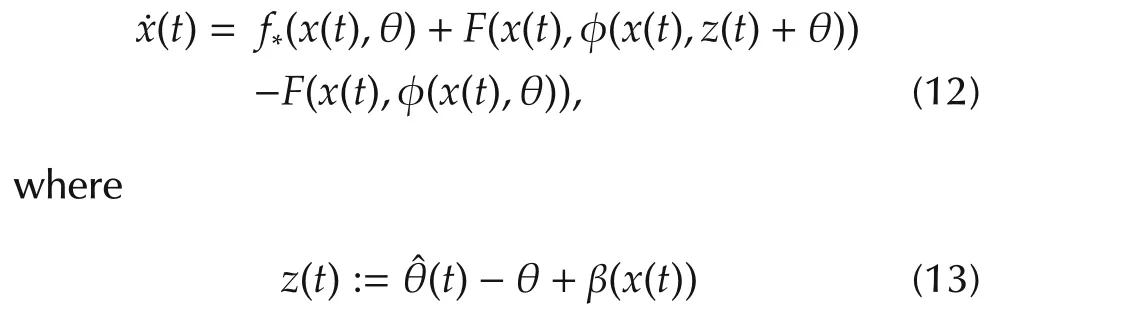
is the off-the-manifold coordinate,with inputz(t),is input-to-state stable[14].

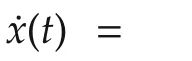
Theorem 1Consider system(1)satisfying Assumption 1,the direct Iamp;I adaptive controller

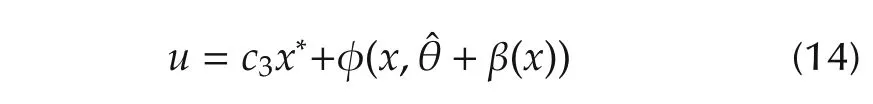
and the estimator

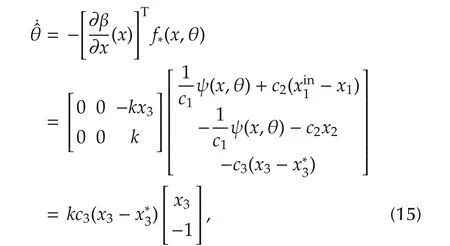
ProofThe objective of adaptation law is to render the manifold asymptotically attractive and invariant,which is achieved by driving the off-the-manifold coordinate(13)to zero.Towards this end,the derivative ofzalong the trajectories of the closed-loop system

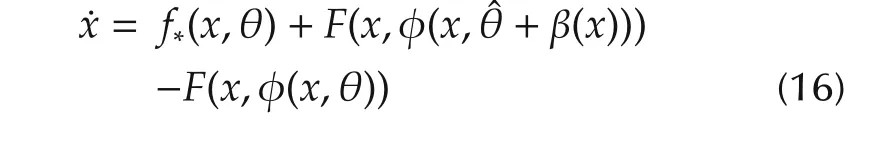
is calculated as

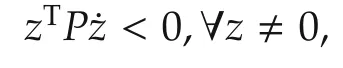
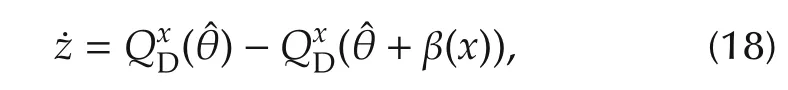
Noting that the definition ofVzand(18),we have

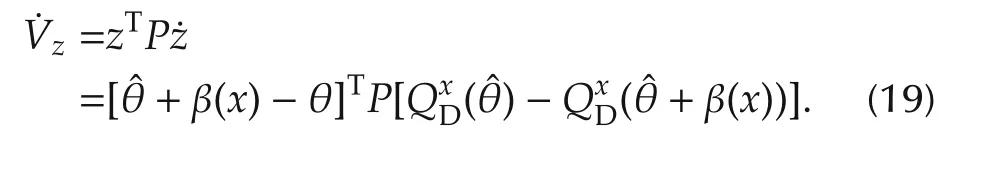
From(19)and β(x)satisfying Assumption 3,the boundedness ofzcan be guaranteed,since the P-monotone makes

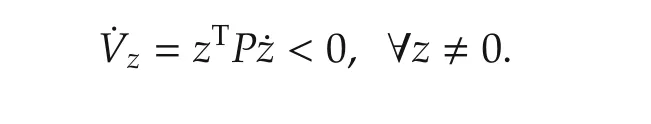
As a result,zconverges to zero as time goes to infinity.

The second part of the proof shows the stability of the perturbed closed-loop system.

Write the closed-loop system(16)in the perturbed form˙x=f∗(x,θ)+ε(x,t),where

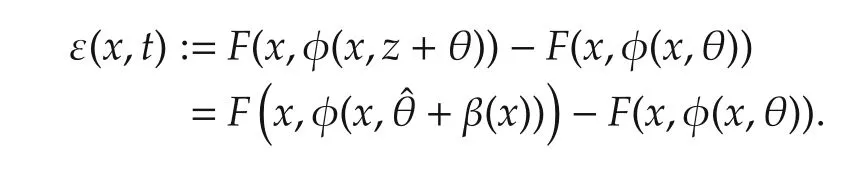
4 Simulation

In this section,a direct Iamp;I adaptive controller is designed for a specified CSTR to verify the effectiveness of the proposed control algorithm.

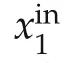
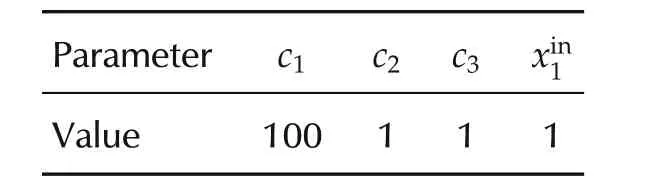
Table 1 The known parameters.

Table 2 Initial conditions of x and

Table 2 Initial conditions of x and

Parameter x1(mol·L−1)x2(mol·L−1)x3(K)ˆθ1ˆθ2 Value 0.2 0.0 300 20 9900

According to the proposed Iamp;I adaptive control law design[11],the specific control law for the given CSTR is designed as follows:

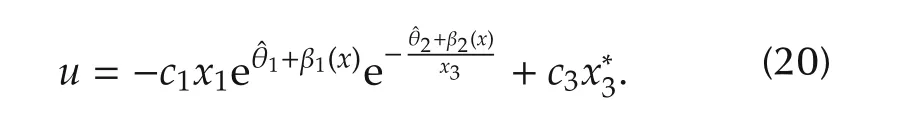
To attenuate the uncertainties in(1),the tuning functions in manifold are chosen as

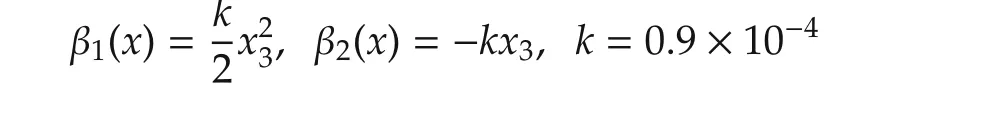
which satisfy Assumption 3 and the corresponding adaptation law is calculated as follows:

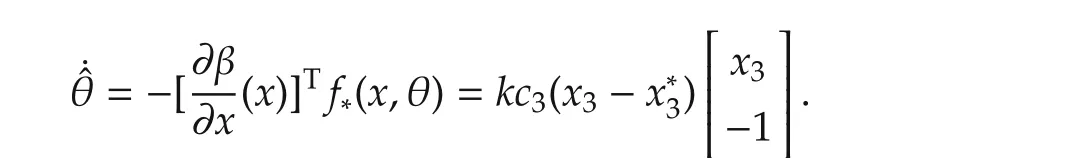
The figures of the simulation shows the evolutions of the allsignalin the closed-loop CSTR.The plots in Figs.1 and 2 show the evolutions of the system state and the tracking error ofx3is given in Fig.3,respectively.Fig.4 shows the control input.The estimates of θ1and θ2are given in Figs.5 and 6,respectively.

As we can observe,the evolutions of the system statexshow good performance in Figs.1 and 2 and the tracking error ofx3is given in Fig.3,which illustrates thatx3converges tox∗3in the presence of nonlinearly parameterized uncertainty ψ(x(t),θ).The plot of control inputu(t)is reasonable in Fig.4.The smooth evolutions of estimates of θ1,θ2are shown in Figs.5 and 6.

Remark 4In Figs.5 and 6,the value of βi(x)+ˆθi(i=1,2)does not converge to θiits true value since the inputsignaldoes notsatisfy persistentexisting condition as has been discussed in[15].

Fig.1 The evolutions of x1 and x2.

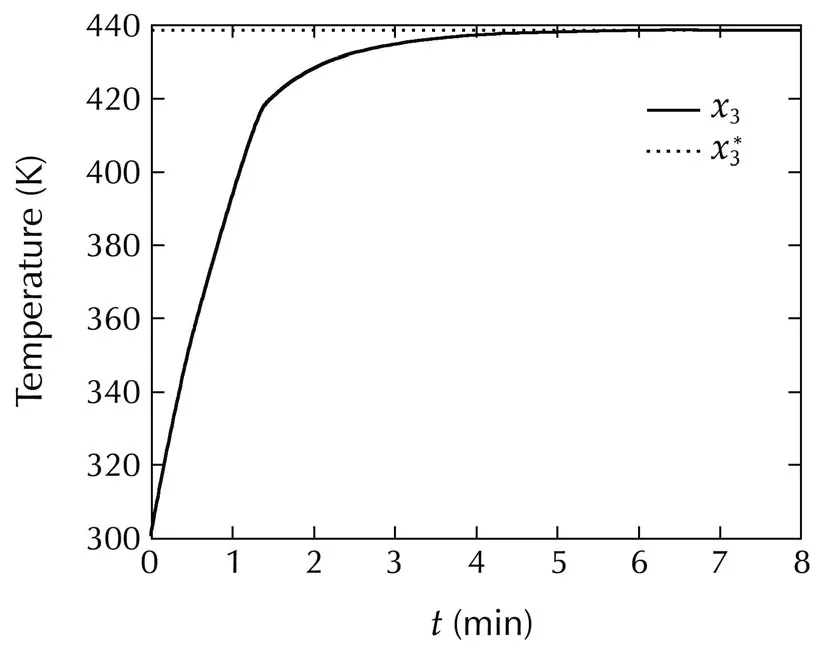
Fig.2 The evolution of x3.

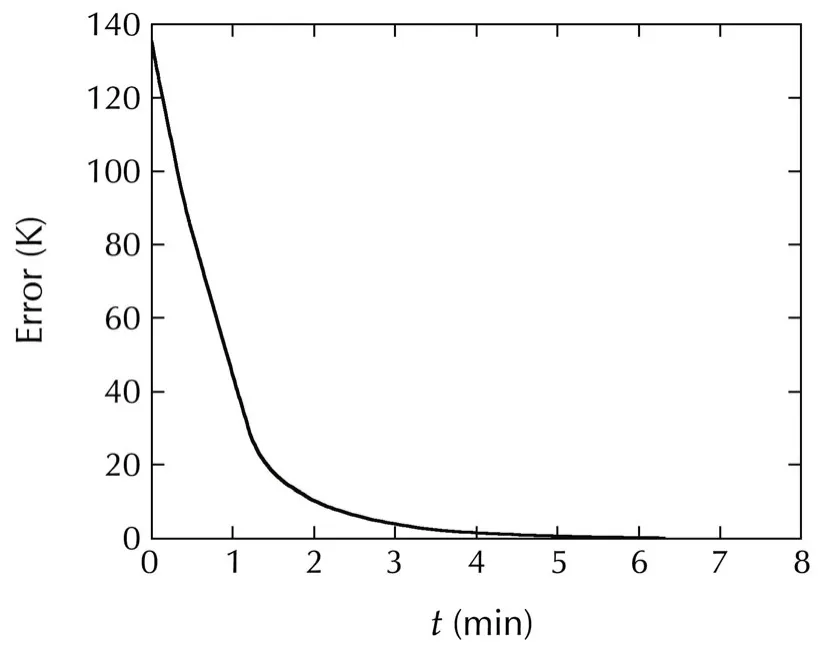
Fig.3 The temperature error e=x∗3 − x3.

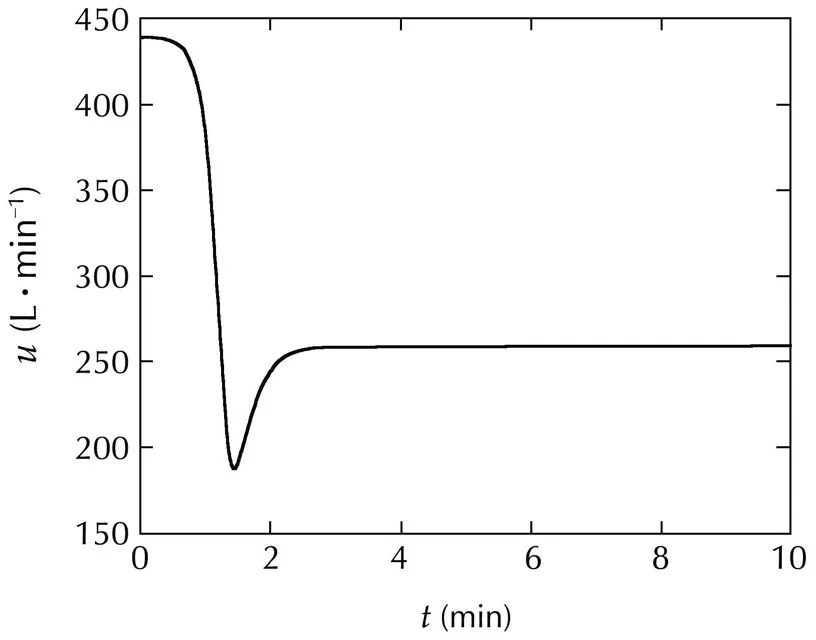
Fig.4 Control inputs.

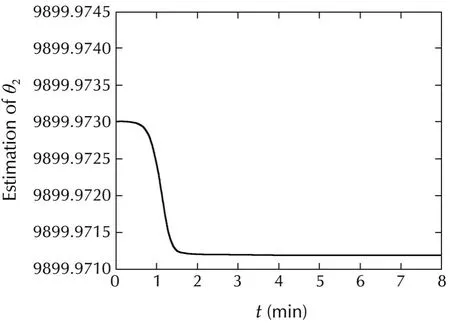
Fig.6 The estimation of θ2.

5 Conclusions

In this paper,an Iamp;I adaptive control algorithm for a class of CSTRs is presented to realize performanceoriented control.The adaptive control includes two parts.First part,the base-line control law using nonlinear contraction method is constructed to render the class of closed-loop CSTRs globally asymptotically stable assuming knowing the unknown parameters.The Second part,the adaptation law is synthesized by Iamp;I method to form such that the off-the-manifold coordinate converges to zero using theP-monotone property,which is enforced by selecting tuning function in manifold.As a result,the system state of the CSTR closed by the presented control law converges to its desired value asymptotically.

[1]S.Salehi,M.Shahrokhi.Adaptive fuzzy backstepping approach for temperature control of continuous stirred tank reactors.Fuzzy Sets and Systems,2009,160(12):1804–1818.

[2]M.Ratto.A theoretical approach to the analysis of PI-controlled CSTRs with noise.Computersamp;Chemical Engineering,1998,22(11):1581–1593.

[3]T.D.Knapp,H.M.Budman,G.Broderick.Adaptive control of a CSTR with a neural network model.Journal of Process Control,2001,11(1):53–68.

[4]H.Zhang,L.Cai.Nonlinear adaptive control using the Fourier integral and its application to CSTR systems.IEEE Transactions on Systems,Man,and Cybernetics–Part B:Cybernetics,2002,32(3):367–372.

[5]F.Viel,F.Jadot,G.Bastin.Robust feedback stabilization of chemical reactors.IEEE Transactions on Automatic Control,1997,42(4):473–481.

[6]R.Gopaluni,I.Mizumoto,S.Shah.A robust nonlinear adaptive backstepping controller for a CSTR.Industrialamp;Engineering Chemistry Research,2003,42(20):4628–4644.

[7]T.Zhang,M.Guay.Adaptive nonlinear control of continuously stirred tank reactor systems.Proceedings of the American Control Conference,Arlington:IEEE,2001:1274–1279.

[8]S.Ge,C.Hang,T.Zhang.Nonlinear adaptive control using neural networks and its application to CSTR systems.Journal of Process Control,1999,9(4):313–323.

[9]A.Fradkov,R.Ortega,G.Bastin.Semi-adaptive control of convexly parametrized systems with application to temperature regulation of chemical reactors.International Journal of Adaptive Control and Signal Processing,2001,15(4):415–426.

[10]A.Astolfi,R.Ortega.Immersion and invariance:a new tool for stabilization and adaptive control of nonlinear systems.IEEE Transactions on Automatic Control,2003,48(4):590–606.

[11]X.Liu,R.Ortega,H.Su,et al.Immersion and Invariance Adaptive Control of Nonlinearly Parameterized Nonlinear Systems.IEEE Transactions on Automatic Control,2010,55(9):2209–2214.

[12]W.Lohmiller,J.-J.E.Slotine.On contraction analysis for nonlinear systems.Automatica,1998,34(6):683–696.

[13]B.Sharma,I.Kar.Contraction based adaptive control of a class of nonlinear systems.Proceedings of the American Control Conference,St Louis:IEEE,1997:808–813.

[14]E.Sontag,A.Teel.Changing supply functions in input/state stable systems.IEEE Transactions on Automatic Control,1995,40(8):1476–1478.

[15]X.Liu,R.Ortega,H.Su,et al.Identification of nonlinearly parameterized nonlinear models:Application to mass balance systems.Joint 48th IEEE Conference on Decision and Control(CDC)and 28th Chinese Control Conference,Shanghai:IEEE,2009:4682–4685.

her B.Sc.degree from Henan University,Kaifeng,China,in 2011.She is pursuing the M.Sc.degree in the School of Electronic Information Engineering,Beijing Jiaotong University,Beijing,China.E-mail:12120248@bjtu.edu.cn.

Xiangbin LIUreceived his B.Sc.degree from Xi’an Institute of Technology,China,in 1995,M.Sc.degree from University of Science and Technology Beijing,China,in 2002,and Ph.D.degree from Zhejiang University,China,in 2009,respectively.He is an associate professor at the School of Electronics and Information Engineering,Beijing Jiaotong University.His research interests include adaptive control,robust control and nonlinear control.E-mail:xbliu@bjtu.edu.cn.

Hongye SUreceived the B.Sc.degree in Industrial Automation from the Nanjing University of Chemical Technology,Jiangsu,China,in 1990,and the M.Sc.and Ph.D.degrees from Zhejiang University,Hangzhou,China,in 1993 and 1995,respectively.He was a lecturer in the Department of Chemical Engineering,Zhejiang University,from 1995 to 1997.From 1998 to 2000,he was an associate professor in the Institute of Advanced Process Control,Zhejiang University.Currently,he is a professor with the Institute of Cyber-Systems and Control,Zhejiang University.His current research interests include robust control,time-delay systems,and advanced process control theory and application.E-mail:hysu@iipc.zju.edu.cn.

†Corresponding author.

E-mail:xbliu@bjtu.edu.cn.Tel.:+86-10-51684105;fax:+86-10-51688617.

This work was supported by National Science Foundation of China(No.61320106009)and Open Research Project of the State Key Laboratory of Industrial Control Technology,Zhejiang University,China(No.ICT1433).

©2015 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg