Topology-preserving flocking of nonlinear agents using optimistic planning

Lucian BU¸SONIU ,Irinel-Constantin MOR˘ARESCU

1.Department of Automation,Technical University of Cluj-Napoca,Memorandumului 28,400114 Cluj-Napoca,Romania;

2.Universit´e de Lorraine,CRAN,UMR 7039 and CNRS,CRAN,UMR 7039,2 Avenue de la Forˆet de Haye,Vandoeuvre-l`es-Nancy,France

Received 22 July 2014;revised 20 January 2015;accepted 20 January 2015

Topology-preserving flocking of nonlinear agents using optimistic planning

Lucian BU¸SONIU1†,Irinel-Constantin MOR˘ARESCU2

1.Department of Automation,Technical University of Cluj-Napoca,Memorandumului 28,400114 Cluj-Napoca,Romania;

2.Universit´e de Lorraine,CRAN,UMR 7039 and CNRS,CRAN,UMR 7039,2 Avenue de la Forˆet de Haye,Vandoeuvre-l`es-Nancy,France

Received 22 July 2014;revised 20 January 2015;accepted 20 January 2015

We consider the generalized flocking problem in multiagent systems,where the agents must drive a subset of their state variables to common values,while communication is constrained by a proximity relationship in terms of another subset of variables.We build a flocking method for general nonlinear agent dynamics,by using at each agent a near-optimal control technique from artificial intelligence called optimistic planning.By defining the rewards to be optimized in a well-chosen way,the preservation of the interconnection topology is guaranteed,under a controllability assumption.We also give a practical variant of the algorithm that does not require to know the details of this assumption,and show that it works well in experiments on nonlinear agents.

Multiagent systems,flocking,optimistic planning,topology preservation

DOI 10.1007/s11768-015-4107-5

1 Introduction

Multi-agent systems such as robotic teams,energy and telecommunication networks,collaborative decision support systems,data mining,etc.appear in many areas of technology.Their component agents usually only have a local,limited view,which means decentralized approaches are necessary to control the overall system.In this decentralized setting,often consensus between the agents is desired,meaning that they must reach agreement on certain controlled variables of interest[1–3].Inspired by the behavior of flocks of birds,researchers studied theflockingvariant of consensus,which only requires consensus on velocities while also using position measurements[3,4].Flocking is highly relevant in e.g.,mobile robot teams[5].

In this paper,we consider a generalized version of the flocking problem,in which agreement is sought for a subset of agent variables,while other variables define the interconnection topology between the agents.These two subsets may,but need not represent velocities and positions.The communication connections between agents are based on a proximity relationship,in which a connection is active when the agents are closer than some threshold in terms of the connectivity variables.Each agent finds control actions(inputs)using the optimistic planning(OP)algorithm from artificial intelligence[6].OP works with discrete actions,like the consensus method of[7],and finds sequences of actions that are near-optimal with respect to general nonquadratic reward functions,for general nonlinear dynamics.The first major advantage of our technique is this inherited generality:it works for any type of nonlinear agents.A controllability property is imposed that,for any connected state,roughly requires the existence of an input sequence which preserves connectivity.We define agent reward functions with separate agreement and connectivity components,and our main analytical result shows that if the connectivity rewards are sufficiently large,the algorithm will preserve the interconnection topology.In interesting cases,the computational complexity of the flocking problem is not larger than if the agent would solve the agreement-only problem.The theoretical algorithm is restrictive in requiring to know the length of action sequences satisfying the controllability property.We therefore also provide a practical algorithm variant which does not use this knowledge,and validate it in simulation to nonholonomic agents and robot arms[8].In the second problem we illustrate that despite our focus on flocking,the method also works in the full-state consensus case.

The main novelty of the OP approach compared to existing methods is that it is agnostic to the specific agent dynamics,and so it works uniformly for general nonlinear agents.In particular,our analysis shows that when a solution that preserves the topology exists(in a sense that will be formalized later),then irrespective of the details of the dynamics the algorithm will indeed maintain the topology.Existing topology preservation results are focused on specific types of agents,mainly linear[9,10],[11,Ch.4],or sometimes nonlinear as in e.g.,[12]where the weaker requirement of connectivity is considered.Our practical flocking algorithm exhibits the same generality,whereas existing methods exploit the structure of the specific dynamics targeted to derive predefined control laws,e.g.,for linear double integrators[3],agents with nonlinear acceleration dynamics[13,14],or nonholonomic robots[12,15].The technical contribution allowing us to achieve these results is the exploitation of the OP algorithm,and of its strong near-optimality guarantees.

The approach presented here is a significantextension of our earlier work[16]:it introduces a new algorithm that is theoretically shown to preserve the topology,and also includes new empirical results for nonholonomic agents.Also related isouroptimistic-optimizationbased approach of[17],which only handles consensus on a fixed graph rather than flocking,and directly optimizes over fixed-length action sequences rather than using planning to exploit the dynamical structure of the control problem.

The remainder of this paper is organized as follows.After formalizing the problem in Section 2 and explaining OP in Section 3,the two variants of the consensus algorithm and the analysis of the theoretical variant are given in Section 4.Section 5 presents the experimental results and Section 6 concludes the paper.

List of symbols and notations

|·| cardinality of argument set;

nnumber of agents;

G,V,E,N graph,vertices,edges,neighbors;

i,jagent indices;

x,u,fstate,action,dynamics;

xa,xcagreement states,connectivity states;

Pcommunication range;

kabsolute time step;

Klength of sequence ensuring connectivity;

udaction sequence of lengthd;

ρ,vreward function,value(return);

γ discount factor;

Δ,Γ agreement reward,connectivity reward;

β weight of connectivity reward;

Toptimistic planning budget;

T,T∗,L tree,near-optimal tree,leaves;

ddepth in the tree(relative time step);

b,ν upper and lower bound on return;

κ branching factor of near-optimal tree.

2 Problem statement

Consider a set ofnagents with decoupled nonlinear dynamicsxi,k+1=fi(xi,k,ui,k),i=1,...,n,wherexianduidenote the state and action(input)of theith agent,respectively.The agents can be heterogeneous:they can have different dynamics and state or input dimensionality.An agent only has a local view:it can receive information only from its neighbors on an interconnection graph Gk=(V,Ek),which can be time-varying.The set of nodes V={1,...,n}represents the agents,and the edges Ek⊆V×V are the communication links.Denote by Ni,k={j|(i,j)∈Ek}the set of neighbors of nodeiat stepk.A path through the graph is a sequence of nodesi1,...,iNso that(il,il+1)∈Ek,1llt;N.The graph is connected if there is a path between any pair of nodesi,j.

The objective can be formalized as

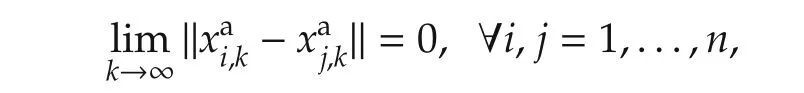
wherexaselects only those state variables for whichagreementis desired,and·denotes an arbitrary norm.We require of course that the selection produces a vector with the same dimensionality for all agents.When all agents have the same state dimension,xa=x,and Ek=E(a fixed communication graph)we obtain the standard full-state consensus problem[1,2].While our technique can be applied to this case,as will be illustrated in the experiments,in the analytical development we will focus on the flocking problem,where the communication network varies with theconnectivitystate variablesxc.Usually,xaandxcdo notoverlap,being e.g.,the agent’s velocity and position[3],so that velocities mustbe synchronized undercommunication constraints dependent on the position.Specifically,we consider the case where a link is active when the connectivity states of two agents are close:

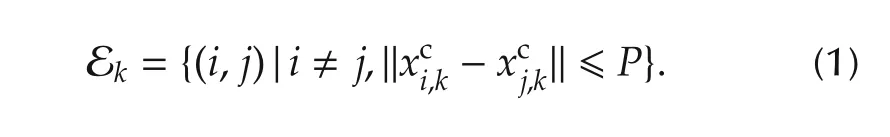
For example whenxcis a position this corresponds to the agents being physically closer than some transmission rangeP.

Our approach requires discretized agent actions.

Assumption1Agentactions are discretized:ui∈Uiwith|Ui|=Mi.

Remark 1Certain systems have inherently discrete and finitely-many actions,because they are controlled by switches.When the actions are originally continuous,discretization reduces performance,but the loss is often manageable.Other authors showed interest in multiagent coordination with discretized actions,e.g.,[7].

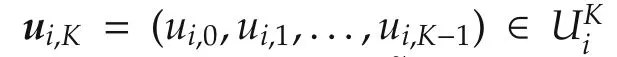
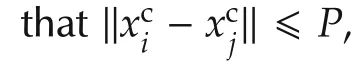
Remark 2This is a feasibility assumption:it is difficult to preserve the topology without requiring such a condition.The condition simply means that for any joint state of the system in which an agent is connected to some neighbors,this agent has an action sequence by which it is again connected afterKsteps,if its neighbors do not move.Therefore,if the assumption does not hold and the problem is such that the neighbors do stay still,the agent will indeed lose some connections and topology cannot be preserved.Of course,in general the neighbors will move,but as we will show Assumption 2 is nevertheless sufficient to ensure connectivity.

K-step controllability properties are thoroughly studied in the literature,e.g.,[18]provide Lie-algebraic conditions to guarantee them.We make a similar assumption in our previous paper[17],where it is however much stronger,requiring thatthe controlis able to move the agent betweenanytwo arbitrary states in a bounded region.With a sufficiently fine action discretization,such an assumption would locally imply Assumption 2 in the present paper.

When making the assumption,we could also use the following definition for the links:

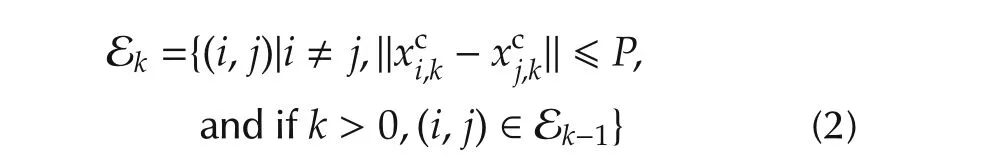
so that the agents never gain new neighbors,and only need to stay connected to their initial neighbors.The analysis will also hold in this case,which is important because with(1),askgrows many or all the agents may become interconnected.For simplicity,we use(1)in the sequel.

3 Background:Optimistic planning for deterministic systems

Consider a(single-agent)optimal control problem for a deterministic,discrete-time nonlinear systemxd+1=f(xd,ud)with statesxand actionsu.Define an infinitelylong action sequenceu∞=(u0,u1,...)and its truncation todinitial actions,u d=(u0,...,ud−1).Given an initial statex0,the return of a sequence is

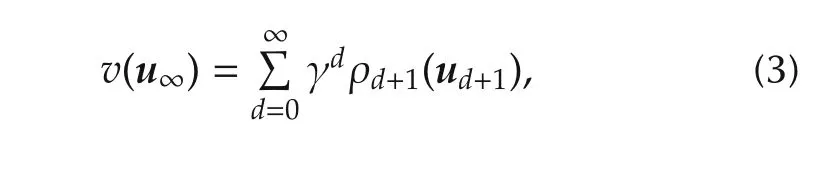
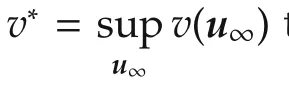
Optimistic planning for deterministic systems(OP)[6,21]explores a tree representation of the possible action sequences from the current system state,as illustrated in Fig.1.It requires a discrete action spaceU=?u1,...,uM?;recall Assumption 1,which ensures this is true forouragents.OP startswith a rootnode representing the empty sequence,and iteratively expandsTwell-chosen nodes.Expanding a node addsMnew children nodes for all possible discrete actions.Each node at some depthdis reached via a unique path through the tree,associated to a unique action sequenceu dof lengthd.We will denote the nodes by their corresponding action sequences.Denote also the current tree by T,and its leaves by L(T).

For a leaf nodeu d,the following gives an upper bound on the returns of all infinite action sequences having in common the initial subsequence up tou d:

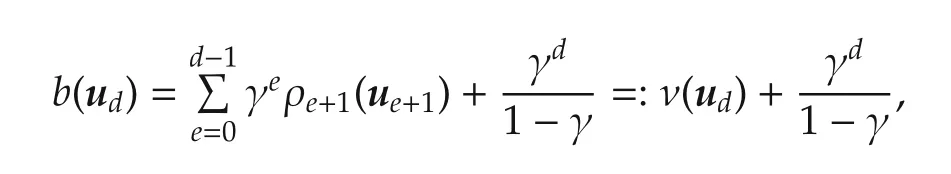
where ν(u d)is a lower bound.These properties hold because all the rewards at depths larger thandare in[0,1].

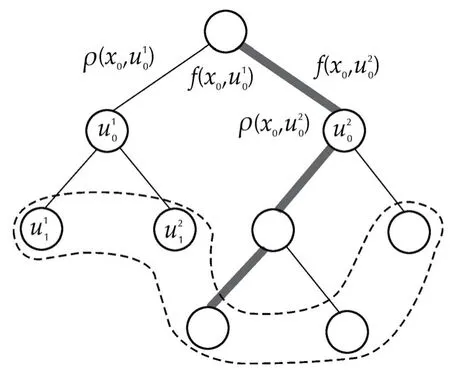
Fig.1 Illustration of an OP tree T.Nodes are labeled by actions,arcs represent transitions and are labeled by the resulting states and rewards.Subscripts are depths,superscripts index the M possible actions/transitions from a node(here,M=2).The leaves are enclosed in a dashed line,while the gray thick path highlights a sequence.

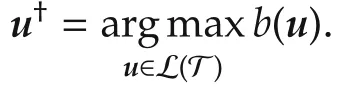
Algorithm 1(Optimistic planning for deterministic systems)Initialize tree:T←?empty sequence u0?;for t=1,...,T do find optimistic leaf:u†← arg max b(u),add to T the children of u†,labeled by u1,...,uM end for;return u∗u∈L(T)d∗,where u∗d∗=arg maxν(u).u∈L(T)

Usually OP and its analysis are developed for timeinvariant reward functions[6,21],such as the quadratic reward exemplified above.However,thisfactis notused in the development,which therefore entirely carriesover to the time-varying case explained here.We provide the algorithm and results directly in the time-varying case,since this will be useful in the consensus context.

To characterize the complexity of finding the optimal sequence from a given statex,we use the asymptotic branching factor of the near-optimal subtree:

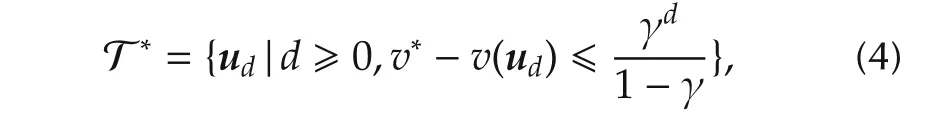
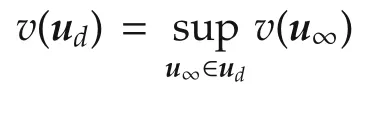
Asequenceudis said to beε-optimalwhenv∗−v(ud)ε.The upcoming theorem is a consequence of the analysis in[6,21].It is given here in a form that brings out the role of the sequence length,useful later.Part i)of the theorem shows that OP returns a long,near-optimal sequence,while part ii)quantifies this length and nearoptimality,via branching factor κ.

Theorem 1When OP is called with budgetT:

i)The lengthd∗of the sequenceu∗

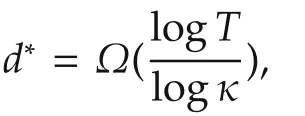
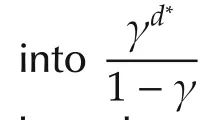
The smaller κ,the better OP does.The best case is κ=1,obtained e.g.,when a single sequence always obtains rewards of 1,and all the other rewards on the tree are 0.In this case the algorithm must only develop this sequence,and suboptimality decreases exponentially.In the worst case,κ=M,obtained e.g.,when all the sequences have the same value,and the algorithm must explore the complete tree in a uniform fashion,expanding nodes in order of their depth.

4 Flocking algorithm and analysis

The OP-based approach to the flocking problem in Section 2 works as follows.At every time stepk,a local optimal control problem is defined for each agenti,using information locally available to it.The goal in this problem is to align the agreement statesxawith those of the neighbors Ni,k,while maintaining the connection topology by staying close to them in terms ofxc.OP is used to near-optimally solve this control problem,and an initial subsequence of the sequence returned is applied by the agent.Then the system evolves,and the procedure is applied again,for the new states and possibly changed graph.

To construct its optimal control problem,each agent needs the predicted behavior of its neighbors.Here,agents will exchange the predicted state sequences resulting from the near-optimalaction sequences returned by OP.Because the agents must act at the same time,how they exchange predictions is nontrivial.If predictions do not match,acoordinationproblem may arise where mismatching actions are applied.Coordination is a difficult challenge in multi-agent systems and is typically solved in model-predictive control by explicit,iterative negotiation over successive local solutions,e.g.,[22].However,it is unlikely that the agents can computationally afford to repeatedly communicate and reoptimize their solutions at every step.Thus we adopt a sequential communication procedure in which agents optimize once per step,similar to the procedure for distributed MPC in[23].We show in Section 4.1 that connectivity can be guaranteed despite this one-shot solution.

To implement the sequential procedure,each agent needs to know its indexias well as the indices of its neighbors.One way to ensure this is an initial,centralized assignment of indices to the agents.Agentiwaits until the neighborsjwithjlt;ihave solved their local optimalcontrolproblemsand found theirpredicted state sequences.These agents communicate their predictions toi.Forjgt;i,agenticonstructs other predictions as described later.Agentioptimizes its own behavior while coordinating with the predictions.It then sends its own,newly computed prediction to neighborsjgt;i.

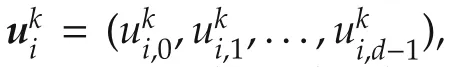
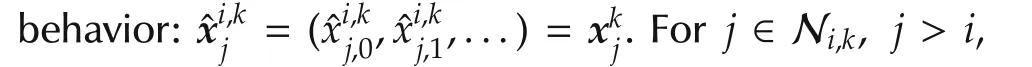
The local optimal control problem of agentiis then defined using the reward function:

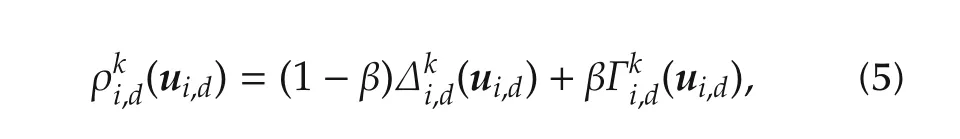
In the implementation,if the agents have their neighbors’models,they could also exchange predicted action sequences instead of states.Since actions are discrete and states usually continuous,this saves some bandwidth at the cost of extra computation to resimulate the neighbor’s transitions up to the prediction length.In any case,itshould be noted thatagents donotoptimize over the actions of their neighbors,so complexity does not directly scale with the number of neighbors.

So far,we have deliberately left open the specific form of the rewards and predictions for neighborsjgt;i.Next,we instantiate them in a theoretical algorithm for which we guarantee the preservation of the interconnection topology and certain computational properties.However,this theoretical variant has shortcomings,so we additionally present a different instantiation which is more suitable in practice and which we later show works well in experiments.

4.1 A theoretical algorithm with guaranteed topology preservation

Our aim in this section is to exploit Assumption 2 to derive an algorithm that preserves the communication connections.We first develop the flocking protocol for each agent,shown as Algorithm 2.Our analysis proceeds by showing that,if sequences preserving the connections exist at a given step,the rewards can be designed to ensure that the algorithm will indeed find one such sequence(Lemma 1).This property is then used to prove topology preservation in closed loop,in Theorem 2.Finally,Theorem 3 shows an interesting computational property of the algorithm:under certain conditions the extra connectivity reward does notincrease the complexity from the case where only agreement would be required.

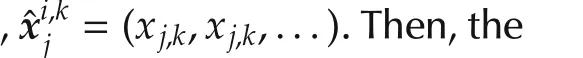
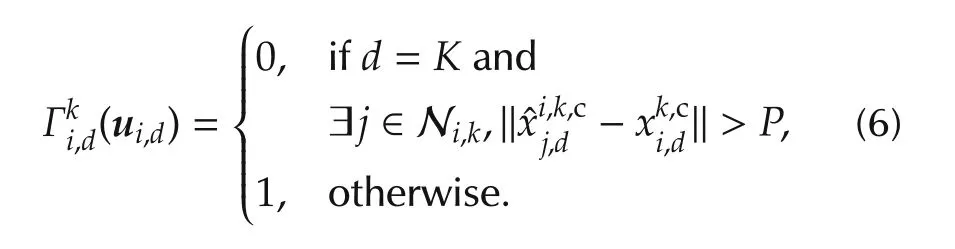
The agreement reward is left general,but to fix ideas,it could be,for instance,

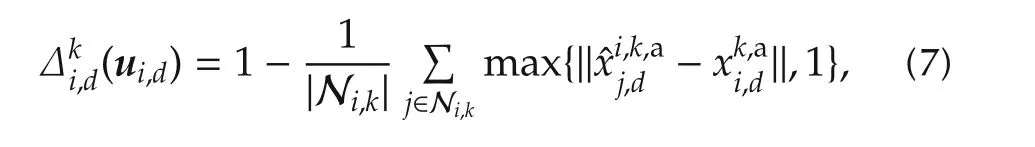
Algorithm 2(OP flocking at agent i–theoretical variant)Set initial prediction x−1i to an empty sequence;for?=0,1,2,...do current step is k←?K,exchange state at k with all neighbors j∈N i,k,send xk−1i to jlt;i,wait to receive new predictionsˆxi,kj from all jlt;i,form predictionsˆxi,kj for jgt;i,run OP with(5)and(6),obtaining uki and xki,send xki to jgt;i,execute K actions uki,0,...,uki,K−1 in open loop end for.

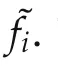
Moving on to the analysis now,we first show that when it is possible,each agent preserves connectivity with respect to the predicted states of its neighbors.

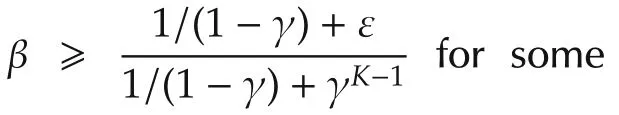
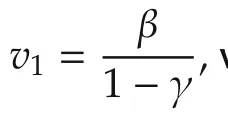
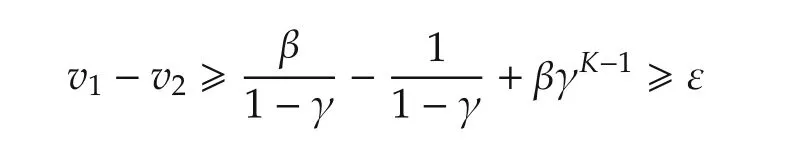
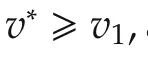
Putting the local guarantees together,we have topology preservation for the entire system,as follows.

Theorem 2Take β andTas in Lemma 1,then under Assumption 2 and if the graph is initially connected,Algorithm 2 preserves the connections at any stepk=?K.

ProofThe intuition is very simple:each agentiwill move so as to preserve connectivity with thepreviousstate of any neighborjgt;i,and then in turnjwill move while staying connected with theupdatedstate ofi,which is what is required.However,since Assumption 2 requires connectivity to hold globally for all neighbors,the formal proof is somewhat technical.

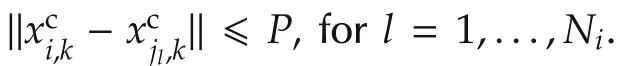
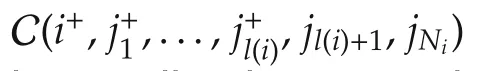
Theorem 2 guarantees that thetopologyis preserved when the initial agent states correspond to a connected network.However,this result does not concern the stability of theagreement.In practice,we solve the agreement problem by choosing appropriately the rewards Δ,such as in(7),so that by maximizing the discounted returnsthe agentsachieve agreement.In Section 5,we illustrate thatthis approach performswellin experiments.Note that Theorem 2 holds whether the graph is defined with(1)or(2).

We will compare performance in the original problem with that in the agreement problem.

Theorem 3Assumev∗=v∗u.For OP applied to theoriginalproblem,the near-optimality bounds of Theorem 1 ii)hold with the branching factor κaof theagreementproblem.

ProofWe startwith a slightmodification to the analysis of OP.For any problem,define the set:

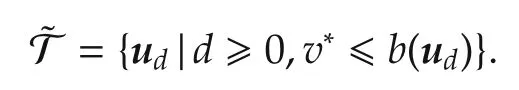
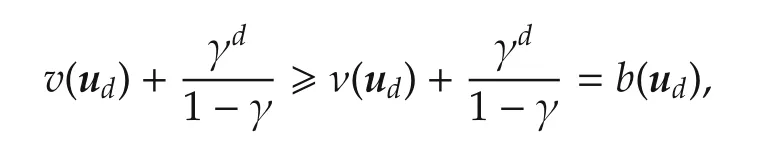
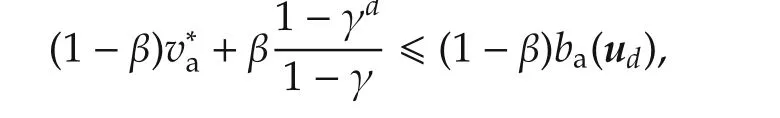
Therefore,finally,

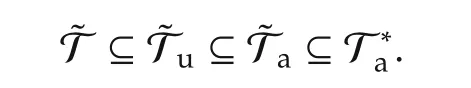
Theorem 3 can be interpreted as follows.If the unconstrained optimal solution would have naturally satisfied connectivity(which is not unreasonable),adding the constraint does not harm the performance of the algorithm,so that flocking is as easy as solving only the agreement problem.This is a nice property to have.

4.2 A practical algorithm

Algorithm 2 has an important shortcoming in practice:it requires knowing a value ofKfor which Assumption 2 is satisfied.Further,keeping predictions constant forjgt;iis safe,but conservative,since better predictions are usually available:those made by the neighbors at previous steps,which may not be expected to change much,e.g.,when a steady state is being approached.

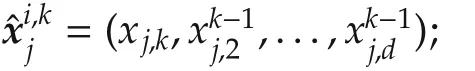
SinceKis unknown,the agent will try preserving connectivity ateverystep,with as many neighbors as possible:

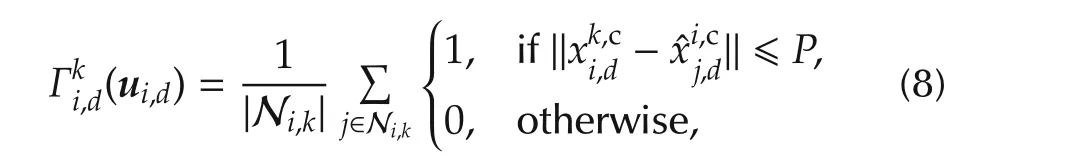
For the links,definition(1)is used,since old neighbors may be lost but the graph may still remain connected due to new neighbors.Therefore,the aim here is only connectivity,weakerthan topology preservation.Forthe agreement component,(7)is employed.Algorithm 3 summarizes the resulting protocol for generic agenti.

A l g o r i t h m 3(O P f l o c k i n g a t a g e n t i–p r a c t i c a l v a r i a n t)S e t i n i t i a l p r e d i c t i o n x−1i t o a n e m p t y s e q u e n c e;f o r s t e p k=0,1,2,...d o e x c h a n g e s t a t e a t k w i t h a l l n e i g h b o r s j∈Ni,k,s e n d xk−1i t o jlt;i,r e c e i v e xk−1j f r o m jgt;i,w a i t t o r e c e i v e n e w p r e d i c t i o n s ˆ xi,kj f r o m a l l jlt;i,f o r m p r e d i c t i o n s ˆ xi,kj f o r jgt;i,r u n O P w i t h(5)a n d(8),o b t a i n i n g uki a n d xki,s e n d xki t o jgt;i,e x e c u t e a c t i o n uk i,0 e n d f o r.

The main advantage of our approach,in both Algorithm 2 and Algorithm 3,is the generality of the agent dynamics it can address.This generality comes at the cost of communicating sequences of states,introducing a dependence of the performance on the action discretization,and a relatively computationally involved algorithm.The time complexity of each individual OP application is between O(TlogT)and O(T2)depending onκ.The overallcomplexity forallagents,ifthey run OP in parallel as soon as the necessary neighbor predictions become available,is largerby a factorequalto the length of the longest path from anyito anyjgt;i.Depending on the current graph this length may be significantly smaller than the number of agentsn.

5 Experimental results

The proposed method is evaluated in two problems with nonlinear agent dynamics.The first problem concerns flocking fora simple type ofnonholonomic agents,where we also study the influence of the tuning parameters of the method.In the second experiment,full-state consensus for two-link robot arms is sought.This experiment illustrates that the algorithm can on the one hand handle rather complicated agent dynamics,and on the other hand that it also works for standard consensus on a fixed graph,even though our analytical focus was placed on the flocking problem.

While both types of agents have continuous-time underlying dynamics,they are controlled in discrete time,as is commonly done in practical computer-controlled systems.The discrete-time dynamics are then the result of integrating the continuous-time dynamics with zero-order-hold inputs.Then,in order for the analysis to hold for Algorithm 2,Assumption 2 must be satisfied by these discretized dynamics.Note that in practice we apply Algorithm 3,and the numerical integration technique introduces modelerrorsthatouranalysis does not handle.

5.1 Flocking of nonholonomic agents

Consider homogeneous agents that evolve on a plane and have the state vectorx=[X Y vθ]withX,Ythe position on the plane(m),vthe linear velocity(m/s),and θ the orientation(rad).The control inputs are the rate of changeaof the velocity and ω of the orientation.The discrete-time dynamics are

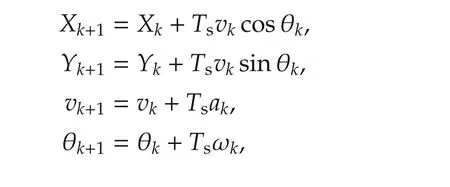
where Euler discretization with sampling timeTswas employed.The aim is to agree onxa=[vθ]T,which represent the velocity vector of the agent,while maintaining connectivity on the plane by keeping the distances between the connectivity statesxc=[X Y]Tbelow the communication rangeP.

The specific multiagent system we experiment with consists of 9 agents initially arranged on a grid with diverging initial velocities,see Fig.2(a).Their initial communication graph has some redundant links.In the reward function,β=0.5 so that agreement and connectivity rewards have the same weight,and the agreement reward is(7)with the distance measure being a 2-norm weighted so that it saturates to 1 at a distance 5 between the agreement states.The range isP=5.The sampling time isTs=0.25 s.

Fig.2 shows that the OP method preserves connectivity while achieving flocking,up to errors due mainly to the discretized actions.The discretized action set was{−0.5,0,0.5}m/s2× {−π/3,0,π/3}rad/s,and the planning budget of each agent isT=300 node expansions.For all the experiments,the discount factor γ is set to 0.95,so that long-term rewards are considered with significant weight.

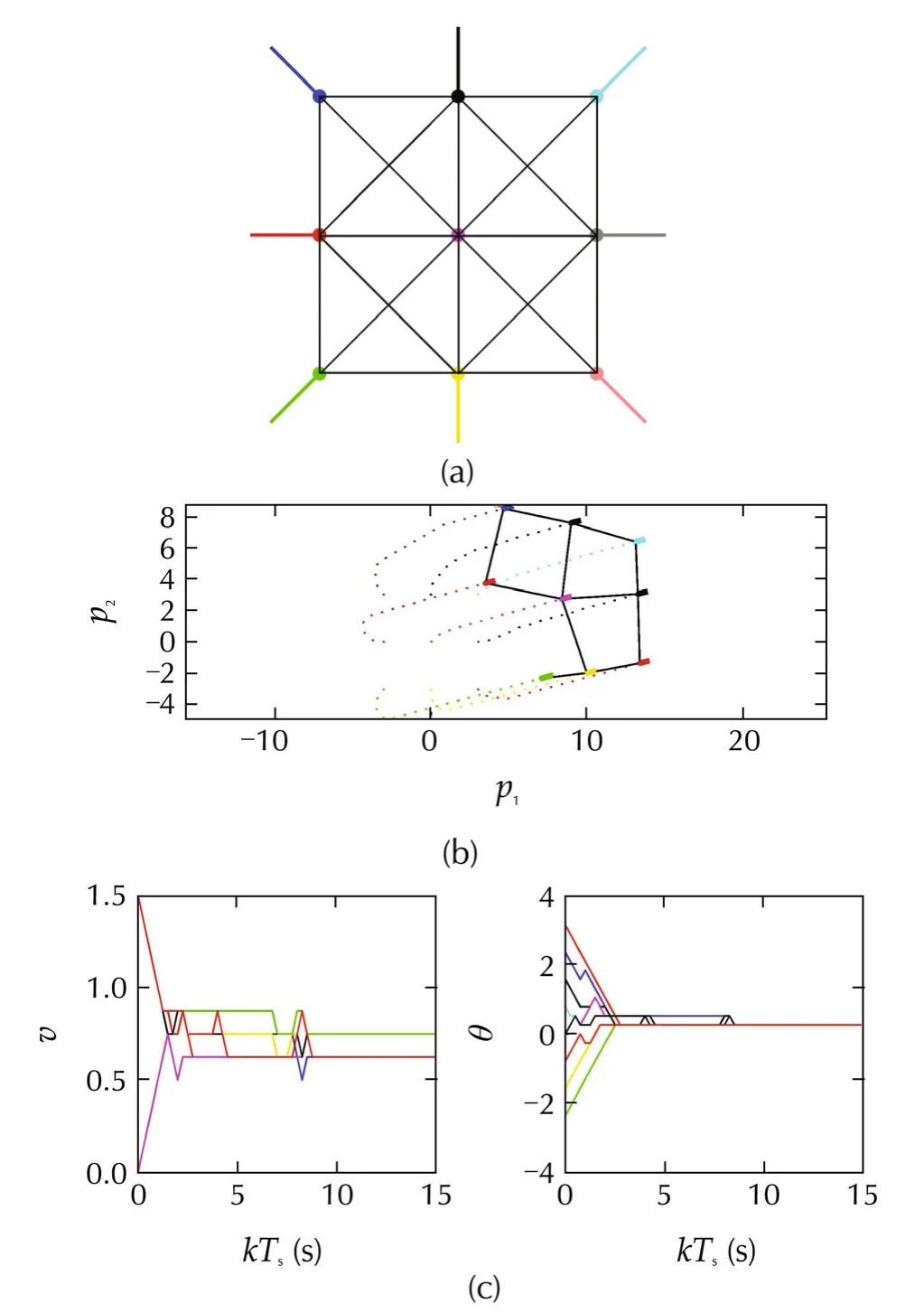
Fig.2 Results for nonholonomic agents.(a)Initial configuration,with the agents shown as colored dots,their initial velocities and orientations symbolized by the thick lines,and their initial graph with thin gray lines,(b)trajectories on the plane,also showing the final configuration of the agents,and(c)evolution of agreement variables.

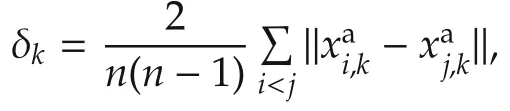
The following budgets are used:T=25,50,75,100,200,...,600,and the length of the predictions is not limited.As shown in Fig.3 and as expected from the theoreticalguarantees ofOP,disagreementlargely decreases withTalthough the decrease is not monotonic1See[24],footnote 4 for an example showing how nonmonotonicity can happen..

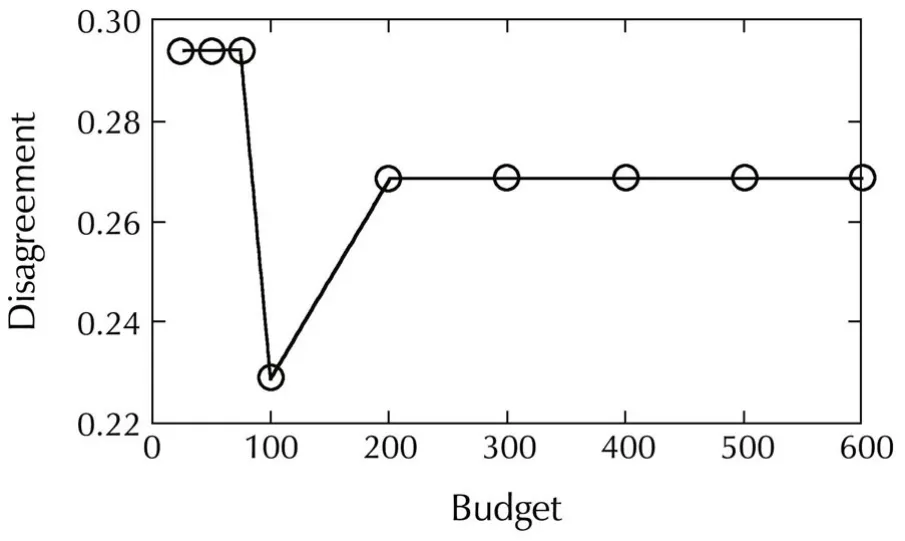
Fig.3 Influence of the expansion budget.

The influence of the prediction length is studied for fixedT=300,by takingL=0,1,3,4 and then allowing full predictions2In effect,predictions with this budget do not exceed length 4 so the last two results will be identical..Fig.4 indicates that performance is not monotonic inL,and medium-length predictions are better in this experiment.While it is expected that too long predictions will not increase performance since they will rarely be actually be followed,the good results for communicating just the current state without any prediction are more surprising,and need to be studied further.

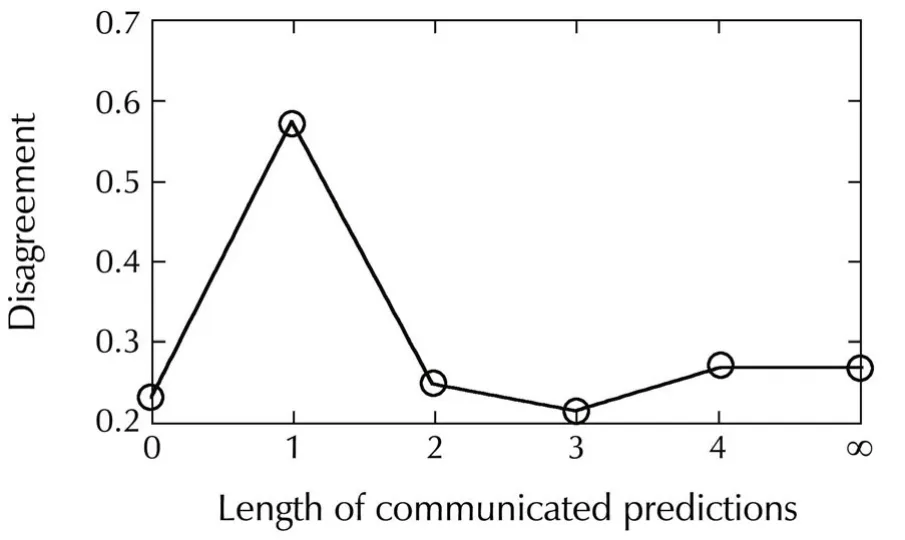
Fig.4 Influence of the maximal prediction length.

5.2 Consensus of robotic arms

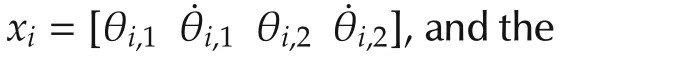
Three robots are connected on a fixed undirected communication graph in which robot 1 communicates with both 2 and 3,but 2 and 3 are not connected.The initial angular positions are taken random with zero initial velocities,see Fig.5.

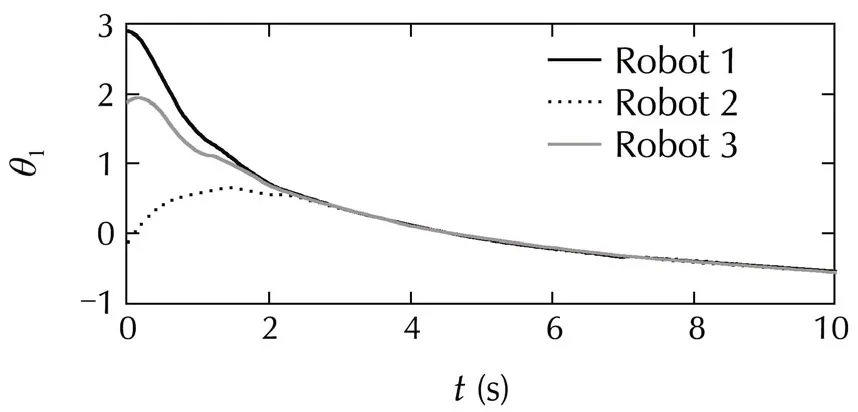
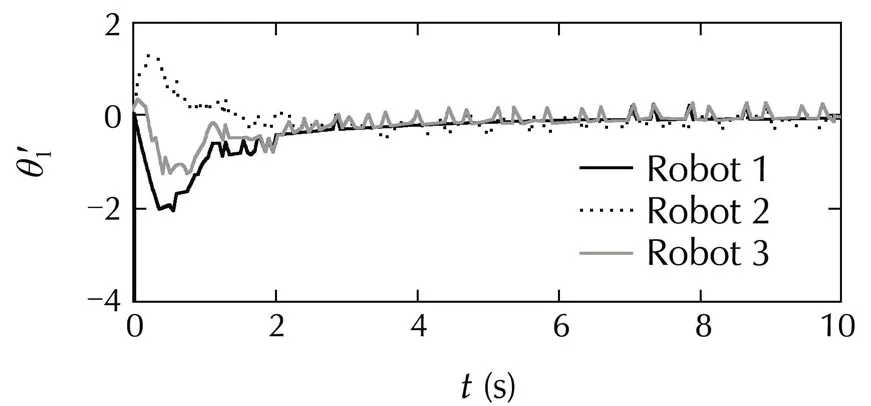
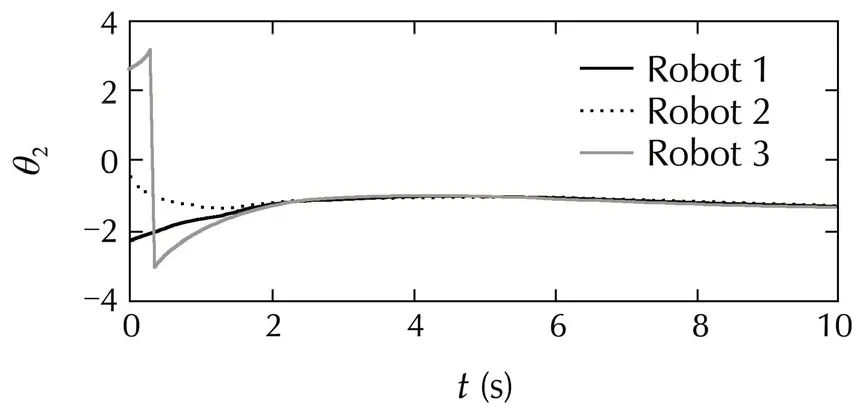
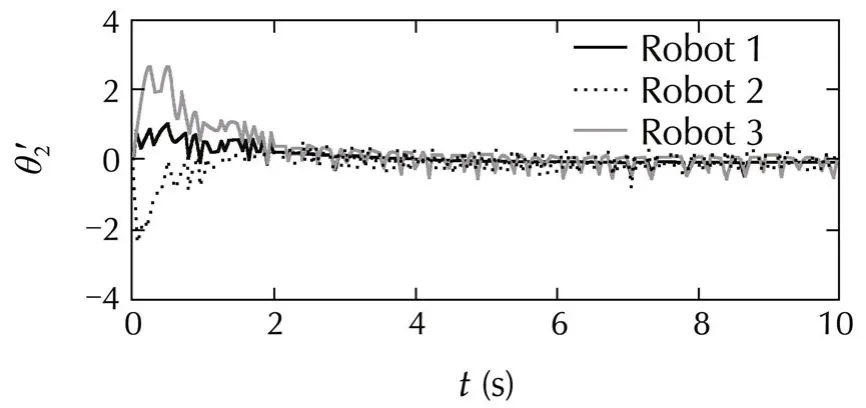
Fig.5 Leaderless consensus of multiple robotic arms:angles and angular velocities for the two links,overimposed for all the robots.Angles wrap around in the interval[−π,π).

The distance measure is the squared Euclidean distance,weighted so that the angular positions are given priority.The discretized actions are{−1.5,0,1.5}N·m×{−1,0,1}N·m,and the budget of each agent isT=400.Consensus is achieved without problems.

6 Conclusions

We have provided a flocking technique based on optimistic planning(OP),which under appropriate conditions is guaranteed to preserve the connectivity topology of the multiagent system.A practical variant of the technique worked well in simulation experiments.

An important future step is to develop guarantees also on the agreement component of the state variable.This is related to the stability of the near-optimal control produced by OP,and since the objective function is discounted such a stability property is a big open question in the optimal control field[26].It would also be interesting to apply optimistic methods to other multiagent problems such as gossiping or formation control.

[1]R.Olfati-Saber,J.A.Fax,R.M.Murray.Consensus and cooperation in networked multiagent systems.Proceedings of the IEEE,2007,95(1):215–233.

[2]W.Ren,R.W.Beard.Distributed Consensus in Multi-vehicle Cooperative Control:Theory and Applications.Communications and Control Engineering.Berlin:Springer,2008.

[3]R.Olfati-Saber.Flocking for multi-agent dynamic systems:Algorithms and theory.IEEE Transactions on Automatic Control,2006,51(3):401–420.

[4]H.G.Tanner,A.Jadbabaie,G.J.Pappas.Flocking in fixed and switching networks.IEEE Transactions on Automatic Control,2007,52(5):863–868.

[5]W.Dong.Flocking of multiple mobile robots based on backstepping.IEEE Transactions on Systems,Man,and Cybernetics–Part B:Cybernetics,2011,41(2):414–424.

[6]J.-F.Hren,R.Munos.Optimistic planning of deterministic systems.Proceedings 8th European Workshop on Reinforcement Learning,Villeneuve d’Ascq,France:Springer,2008:151 – 164.

[7]C.De Persis,P.Frasca.Robust self-triggered coordination with ternary controllers.IEEE Transactions on Automatic Control,2013,58(12):3024–3038.

[8]J.Mei,W.Ren,G.Ma.Distributed coordinated tracking with a dynamic leader for multiple Euler-Lagrange systems.IEEE Transactions on Automatic Control,2011,56(6):1415–1421.

[9]M.M.Zavlanos,G.J.Pappas.Distributed connectivity control of mobile networks.IEEE Transactions on Robotics,2008,24(6):1416–1428.

[10]M.Fiacchini,I.C.Mor˘arescu.Convex conditionson decentralized control for graph topology preservation.IEEE Transactions on Automatic Control,2014,59(6):1640–1645.

[11]F.Bullo,J.Cort´es,S.Martinez.Distributed Control of Robotic Networks:A Mathematical Approach to Motion Coordination Algorithms.Princeton:Princeton University Press,2009.

[12]J.Zhu,J.Lu,X.Yu.Flocking of multi-agent non-holonomic systems with proximity graphs.IEEE Transactions on Circuits and Systems,2013,60(1):199–210.

[13]H.Su,G.Chen,X.Wang,et al.Adaptive second-order consensus of networked mobile agents with nonlinear dynamics.Automatica,2011,47(2):368–375.

[14]J.Zhou,X.Wu,W.Yu,et al.Flocking of multi-agent dynamical systems based on pseudo-leader mechanism.Systemsamp;Control Letters,2012,61(1):195–202.

[15]H.Tanner,A.Jadbabaie,G.Pappas.Flocking in teams of nonholonomic agents.Cooperative Control.V.Kumar,N.Leonard,A.Morse(eds.),Berlin:Springer,2005:458–460.

[16]L.Bu¸soniu,C.Mor˘arescu.Optimistic planning for consensus.Proceedings of the American Control Conference,Washington D.C.:IEEE,2013:6735–6740.

[17]Lucian Bu¸soniu,C.Mor˘arescu.Consensus for blackbox nonlinear agents using optimistic optimization.Automatica,2014,50(4):1201–1208.

[18]B.Jakubczyk,E.D.Sontag.Controllability of nonlinear discretetime systems:A Lie-algebraic approach.SIAM Journal of Control and Optimization,1990,28(1):1–33.

[19]R.S.Sutton,A.G.Barto.ReinforcementLearning:An Introduction.Cambridge,MA:MIT Press,1998.

[20]F.Lewis,D.Liu,eds.Reinforcement Learning and Approximate Dynamic Programming for Feedback Control.Hoboken:John Wileyamp;Sons,2012.

[21]R.Munos.The optimistic principle applied to games,optimization and planning:Towards foundations of Monte-Carlo tree search.Foundations and Trends in Machine Learning,2014,7(1):1–130.[22]R.R.Negenborn,B.De Schutter,H.Hellendoorn.Multi-agent model predictive control for transportation networks:Serial versus parallel schemes.Engineering Applications of Artificial Intelligence,2008,21(3):353–366.

[23]J.Liu,X.Chen,D.M.de la Pe˜na,et al.Sequential and iterative architectures for distributed model predictive control of nonlinear process systems.American Institute of Chemical Engineers(AIChE)Journal,2010,56(8):2137–2149.

[24]L.Bu¸soniu,R.Munos,Robert Babuˇska.A review of optimistic planning in Markov decision processes.Reinforcement Learning and Adaptive Dynamic Programming for Feedback Control.F.Lewis,D.Liu(eds.),Hoboken:John Wileyamp;Sons,2012:DOI 10.1002/9781118453988.ch22.

[25]L.Bu¸soniu,D.Ernst,B.De Schutter,et al.Approximate dynamic programming with a fuzzy parameterization.Automatica,2010,46(5):804–814.

[26]B.Kiumarsi,F.Lewis,H.Modares,et al.Reinforcement Q-learning for optimal tracking control of linear discrete-time systems with unknown dynamics.Automatica,2014,50(4):1167–1175.

the M.Sc.degree(valedictorian)from the Technical University of Cluj-Napoca,Cluj-Napoca,Romania,in 2003,and the Ph.D.degree(cum laude)from the Delft University of Technology,Delft,the Netherlands,in 2009.He is an associate professor with the Department of Automation,Technical University of Cluj-Napoca,Romania.His research interests include planning-based methods for nonlinear optimal control,reinforcement learning and dynamic programming with function approximation,multi-agent systems,and,more generally,intelligent and learning techniques for control.He has authored a book as well as a number of journals,conferences,and chapter publications on these topics.Dr.Bu¸soniu was the recipient of the 2009 Andrew P.Sage Award for the best paper in the IEEE Transactions on Systems,Man,and Cybernetics.E-mail:lucian@busoniu.net.

Irinel-ConstantinMOR˘ARESCUis currently an associate professor at Universit´e de Lorraine and a researcher at the Research Centre of Automatic Control(CRAN UMR 7039 CNRS)in Nancy,France.He received the B.Sc.and the M.Sc.degrees in Mathematics from University of Bucharest,Romania,in 1997 and 1999,respectively.In 2006,he received the Ph.D.degree in Mathematics and Technology of Information and Systems from University of Bucharest and University of Technology of Compi`egne,respectively.His works concern stability and controloftime-delay systems,tracking control for nonsmooth mechanical systems,consensus and synchronization problems.E-mail:constantin.morarescu@univ-lorraine.fr.

†Corresponding author.

E-mail:lucian@busoniu.net.

This work was supported by a Programme Hubert Curien-Brancusi cooperation grant(CNCS-UEFISCDI contract no.781/2014 and Campus France grant no.32610SE).Additionally,the work of L.Bu¸soniu was supported by the Romanian National Authority for Scientific Research,CNCS-UEFISCDI(No.PNII-RU-TE-2012-3-0040).The work of I.-C.Mor˘arescu was partially funded by the National Research Agency(ANR)project“Computation Aware Control Systemsquot;(No.ANR-13-BS03-004-02).

©2015 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg