（G′／G）展开法求解（2＋1）维PBLMP方程的新精确解

袁萍 （长江大学文理学院，湖北 荆州434020）

1 引言

孤立子、浑沌、分形等非线性现象普遍存在于自然科学和社会科学中，而这些现象大都可以通过建立非线性偏微分方程来描述。因此，对非线性偏微分方程精确解的研究已经成为一项重要工作。为解决非线性问题，目前已形成较多的求解方法，如齐次平衡法［1，2］、Backlund变换［3］、逆散射方法［4］等。近年来，G′／G展开法［5］也被提出，该方法具有直接、简洁的特点，能有效地求解许多非线性偏微分方程。

考虑（2＋1）维Potential Boiti－Leon－Manna－Pempinelli方程（PBLMP方程）［6］：

文献 ［7］对PBLMP方程进行了painleve分析，得到了该方程的Lax对和精确解；文献 ［8，9］通过多线性分离变量法得到该方程的钟型解和含2个任意函数的分离变量解；文献 ［10］利用经典李群方法得到了方程的4组相似约化，进而得到了方程的有理函数解、Jacobi椭圆函数解、双曲函数解与三角函数解。下面，笔者利用（G′／G）展开法研究了（2＋1）维PBLMP方程，利用Maple软件得到方程的一些新精确解。

2 PBLMP方程新精确解的求解过程

为了求解方程（1），令：

代入方程（1）得：

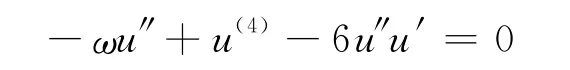
将方程两边同时对ξ积分一次，并置积分常数为0，得：

设方程（2）的解为：

式中，m为正整数；ai与a－i不同时为0；G＝G（ξ）满足二阶常微分方程：

结合式（4），将式（3）代入方程（2），由齐次平衡原理，考虑到方程（2）中最高阶导数u‴与非线性项－3（u′）2的齐次平衡，得，则m＋3＝2（m＋1），得m＝1。记＝p，则：

其中：

将式（5）代入方程（2），并结合式（6），合并p的同次幂，并令其系数为0，得到一组关于a－1，a0，a1，λ，μ，ω的代数方程组：

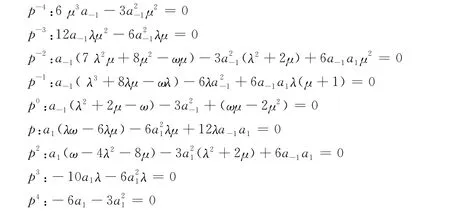
利用Maple求解上面的方程组，得到以下4组系数关系：

（i）λ＝0，ω＝－4μ，a－1＝0，a1＝－2，μ和a0为任意常数；

（ii）λ＝0，ω＝－16μ，a－1＝2μ，a1＝－2，μ和a0为任意常数；

（iii）ω＝λ2－4μ，a－1＝2μ，a1＝0，λ、μ、a0为任意常数；

（iv）λ＝0，μ＝0，ω＝－3a－1，a1＝0，a0和a－1为任意常数。

1）将λ＝0，ω＝－4μ，a－1＝0，a1＝－2代入式（5），得到方程（1）的通解：

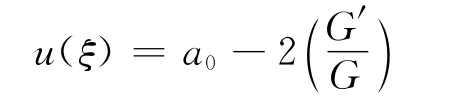
其中，G满足G″＋μG＝0；ξ＝x＋y＋4μt；μ，a0为任意常数。

当μ＜0时，由G″＋μG＝0有：

得方程（1）的双曲函数解：

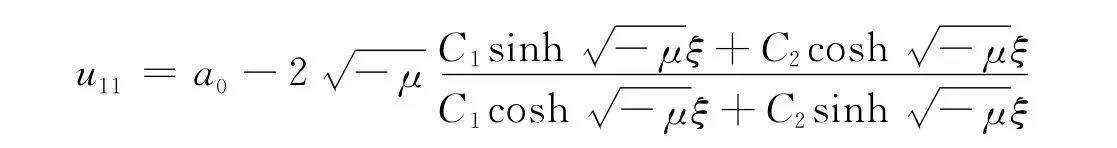
特别地，当C1≠0，C2＝0时，u11＝a0－2，解的形式与文献［10］相同。

当μ＞0时，由G″＋μG＝0有：

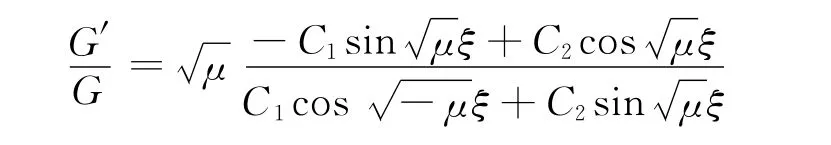
得方程（1）的三角函数解：

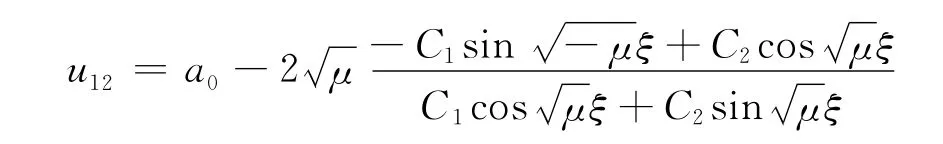
特别地，当C1≠0，C2＝0时，u12＝a0＋2，解的形式与文献［10］相同。

2）将λ＝0，ω＝－16μ，a－1＝2μ，a1＝－2代入式（5），得到方程（1）的通解：

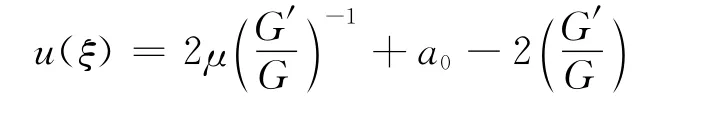
其中，G满足G″＋μG＝0；ξ＝x＋y＋16μt。

当μ＜0时，得方程（1）的双曲函数解：

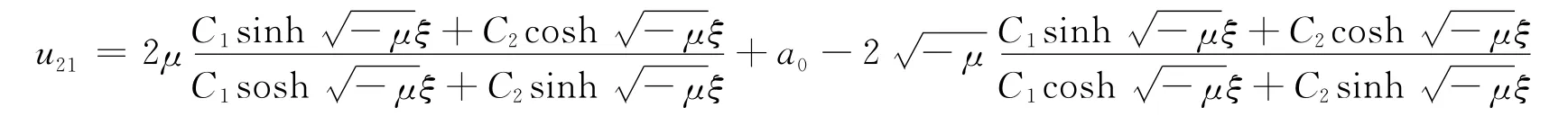
当μ＞0时，得方程（1）的三角函数解：

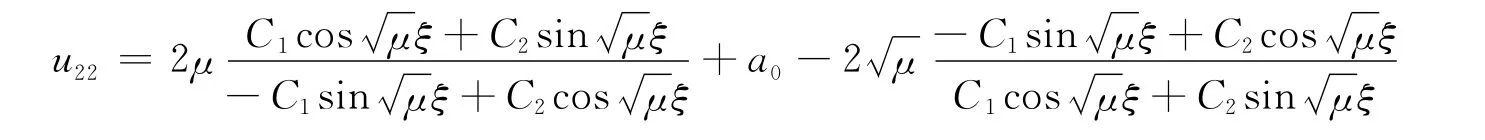
3）将ω＝λ2－4μ，a－1＝2μ，a1＝0代入式（5），得到方程（1）的通解：

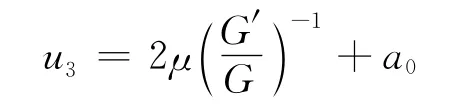
其中，G满足G″＋λG′＋μG＝0；ξ＝x＋y＋（λ2－4μ）t；λ为任意常数。

当λ2－4μ＞0时，由G″＋λG′＋μG＝0有：

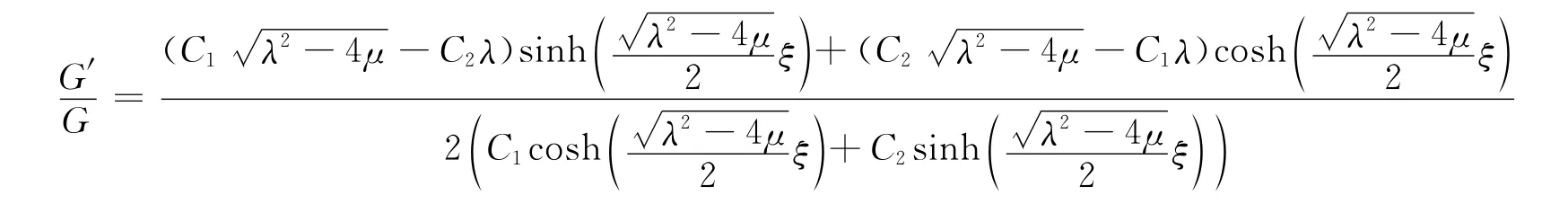
得方程（1）的双曲函数解：

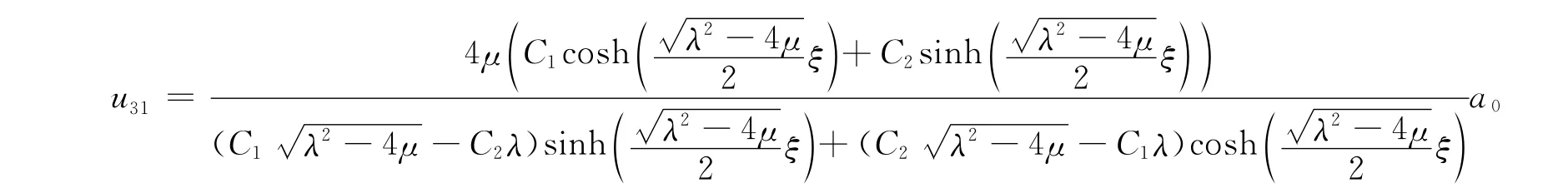
当λ2－4μ＜0时，由G″＋λG′＋μG＝0有：

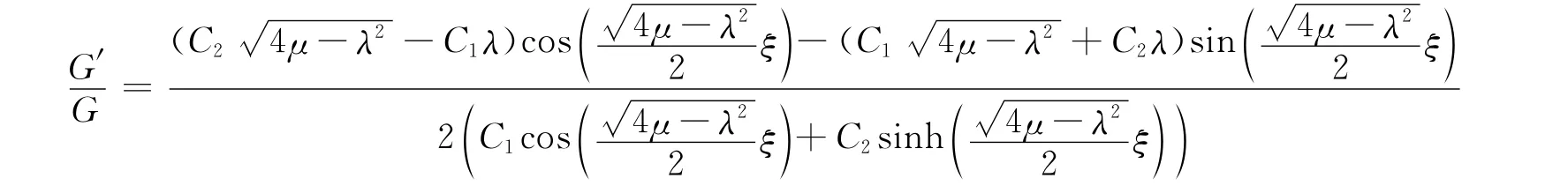
得方程（1）的三角函数解：

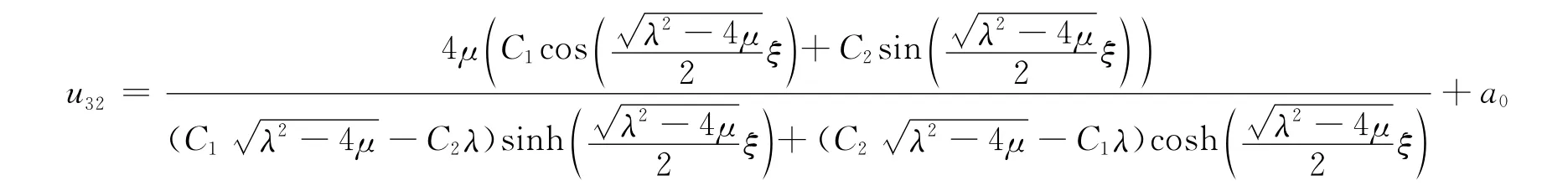
当λ2－4μ＝0时，方程（1）的解没有实际物理意义，不作讨论。

3 结语

利用G′／G展开法对（2＋1）维PBLMP方程进行求解，得到了方程一些与文献 ［8～10］形式不同的新解，拓展了G′／G展开法的应用，丰富了（2＋1）维PBLMP方程的解的形式。从求解的过程可以看出，G′／G展开法具有简洁、直接的特点，此法也可以推广到求更为复杂的非线性偏微分方程的其他精确解。

［1］Wang M L.Exact Solutions for a Compound Kdv－Burgers Equation ［J］.Physics Letters A，1996，213（5－6）：279～287.

［2］王明亮，李志斌，周宇斌 .齐次平衡原理及其应用 ［J］.兰州大学学报（自然科学版），1999，35（3）：8～16.

［3］曾昕，张鸿庆 .（2＋1）维Boussinesq方程的Banklund变换与精确解 ［J］.物理学报，2005，54（4）：1476～1480.

［4］Ablowitz M J P，Clarkson P A.Solitons Nonlinear Evolution Equations and Inverse Scattering ［M］.New York：Cambridge University Press，1991.

［5］Wang M L，li X Z，ZhanG J L.The（G′／G）－Expansion Method and Travelling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics［J］.Physics Letters A，2008，372（4）：417～423.

［6］Dai C Q，Zhou G Q.Exotic Interactions between Solution of the（2＋1）－dimensional Asymmetric Nizhnik－Noyikov－Veselov Systems ［J］.Chinese Physics，2007（615）：1201.

［7］Estevez P G，Lebles.A Wave Equation in 2＋1：Painleve Analysis and Solutions ［J］.Inverse Problems，1995，11（4）：925.

［8］Tang X Y，Lou S Y，Zhang Y.Localized Excitations in（2＋1）－dimensional Systems ［J］.Physical Review E，2002，66（4）：46～60.

［9］Lou S Y，Tang X Y.Methods of Nonlinear Mathematical Physics ［M］.BeiJing：Science Press，2006.

［10］刘勇，刘希强，王振立 .（2＋1）维Potential Boiti－Manna－Pempinelli方程的对称、约化和精确解 ［J］.量子电子学报，2014（31）：533～540.