联系数的一种新的取值方法及其应用

梅晓玲，谢承荣 （郧阳师范高等专科学校数学与财经系，湖北 十堰442000）

保加利亚学者K.T.Atanassov在1999年将仅考虑隶属度的Zadeh模糊集［1］推广到同时考虑隶属度、非隶属度和犹豫度3个方面，提出了直觉模糊集［2］的概念。相比模糊集，直觉模糊集更能形象描述与刻画现实生活中的许多不确定性问题，受到学者们的关注和重视，并取得了不少研究成果。但如何深刻地认识模糊不确定性的本质，并且客观地用适当的数学工具来研究模糊问题中的不确定性是要深入研究的课题。联系数［3］可用于处理模糊、随机、中介和信息不完全所致不确定性问题，联系数理论为研究模糊问题中的不确定性提供新的思路。以联系数为工具研究直觉模糊集的关键是联系数中i的取值问题，笔者在已有的i的取值方法基础上，利用IF点算子提出新的i的取值方法。

1 联系数的概念

联系数是把给定范围内确定性和不确定性联系起来的一种数，其把不确定性与确定性作为一个整体，系统地进行数学处理和辨证分析。联系数的定义式为：

在联系数μ的定义式中，i和j有双重意义［4，5］。

第1个含义是称j为对立系数。j在计算时、取j＝－1；i称为差异系数，i∈［－1，1］且是不确定取值。a称为同一数（同一度），b称为差异数（差异度），c称为对立数（对立度），分别是关于所研究的对象系统的同一性测度、差异性测度和对立性测度。联系数的意义在于把研究对象的同一性测度（同一数）、差异性测度（差异数）和对立性测度（对立数）联系在一起，组成一个同异反系统。在联系数意义下，不仅在宏观上有a＋b＋c＝1这一约束，而且由于j＝－1，i∈［－1，1］同时又刻划出a，b，c在微观层次上的互相联系，互相渗透，因而具有丰富的系统信息。第2个含义是不计较i和j的取值情况，此时仅起标记的作用。关于联系数的运算法则，这里只列举笔者研究所需要的加法、数乘运算及大小比较［4］。

1）加法运算：

2）常数与联系数的乘积：

3）大小比较方法。设u1＝a1＋b1i＋c1j，u2＝a2＋b2i＋c2j，则：

若i∈I⊆［－1，1］时，u1－u2＞0，则在i∈I这个范围内有u1＞u2。同理，u1－u2＜0时，u1＜u2。

2 联系数与直觉模糊数的关系

联系数与直觉模糊数关系密切，在概念、组织形式、应用上有所不同，但在研究刻画不确定系统时有着异曲同工之妙［6］。

联系数μ＝a＋bi＋cj（a＋b＋c＝1），只考虑了离散型且为有限的情况，现在将其推广到一般的离散与连续情形。

对于i∈［－1，1］，i＝－1，i、j仅起标记作用时可以用类似于“内积”的运算求得μ，即：

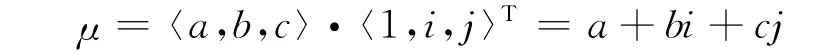
用闭区间［0，1］上的2个函数μA（x），νA（x）分别表示论域X上的任意元素x对问题A的支持和反对的证据，即为联系数表达式中的同一度与对立度，且满足μA（x）＋νA（x）≤1；函数 πA（x）＝1－μA（x）－μA（x）为元素x支持A与否的不确定程度，现为联系数表达式中的差异度，由此联系数与直觉模糊数结合起来，表达式可改写为：

其中，μA（x）＋πA（x）＋νA（x）＝1，πA（x）可以由μA（x），νA（x）确定，即由同一度和对立度来确定差异度（不确定度）。

用表达式μ（A）＝μA（x）＋πA（x）i＋νA（x）j来表达元素x符合A的隶属程度，将联系数和直觉模糊数进一步结合，结合的过程可以说明联系数是直觉模糊（IFS）理论的扩展，而直觉模糊（IFS）是联系数的又一种形式。

3 联系数新的取值方法

联系数表达式μ（A）＝a＋bi＋cj辨证且系统地描述了不确定性，表达式中不确定项bi的给出是关键之处，在一定的条件下用其来对“弃权”这种不确定性进行分解，这里i的取值将弃权中的同一与对立分离出来，定量分析其中的赞同、反对的程度。

直觉模糊集中的犹豫指数πA（x）＝1－μA（x）－νA（x）为x支持A与否的不确定程度，也为联系数表达式中的差异度。直觉模糊集的3个构成指标用投票模型来解释即为赞成、反对和弃权，这里弃权所造成的不确定性对决策的结果会产生直接影响，所以考虑将弃权部分的信息尽可能准确化，由此思考利用IF点算子［7］对“弃权”问题进行深度挖掘与剖析，提高决策的准确性，降低模糊指标的不确定性对决策带来的影响。

将一直觉模糊集A转化为带有如下直觉指数：

从而得到新的赞成、反对和弃权票的比例分别为μA（x）＋αuπA（x），νA（x）＋βuπA（x）和（1－αu－βu）πA（x）。这里，对任意A∈IFS（U），αu，βu∈ ［0，1］，且αu＋βu＜1。

显然对任意x∈U，有≤πA（x），对A∈IFS（U），若记：

则：

进一步有：

推广到一般情形，对任意正整数n有：

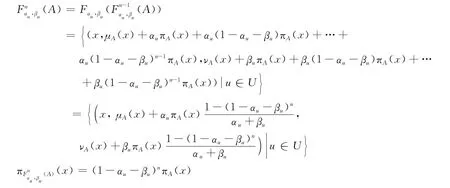
由上面的分析可以得到联系数表达式中i的取值方法：

则得到新的联系数取值方法，即：

这里得到的新的i的取值方法中，若取n＝1，αu＝μA（u），βu＝νA（u）时，取值结果与顺势取值法［7］相同。

一般地取：

也即x符合A的隶属程度：

4 实例分析

例1（空调系统选择问题［8］） 假设有3种空调系统（方案）a1、a2、a3，在选择过程中需要考虑3种属性：u1代表经济属性，u2代表功能，u3代表有效性。已知决策矩阵如表1所示，属性权重为w1＝0.4751，w2＝0.2786，w3＝0.2463。

表1 决策矩阵～X

由联系数的概念，利用笔者提出的i的取值方法取：

将各方案的直觉模糊属性值由式（1）转化为联系数值，然后将得到的各属性联系数值加权求和：

由联系数的大小方法可知方案的排序为：

该结果与文献［6］的结果相同，但比较这2种方法的计算过程，笔者提出的方法大大简化了计算过程，减小了计算量，快速准确。

5 结语

以联系数为工具研究不确定性问题的关键是联系数中i的取值问题，笔者提出的联系数的取值方法对直觉模糊集的犹豫度（不确定性）进行了更准确、更细致的挖掘，不确定性问题的准确性得到进一步提高。但如何深刻地认识模糊不确定性的本质，对不同类型的不确定性问题选择合适的数学工具进行精确与量化需要更进一步的深入研究。

［1］Zadeh L A.Fuzzy sets［J］.Inform and Control，1965，8（3）：338～353.

［2］Atanassov K T.Intuitionistic fuzzy sets ［J］.Fuzzy Sets and Systems，1986，20：87～96.

［3］赵克勤 .集对分析及其应用 ［M］.杭州：浙江科学技术出版社，1992：68～80.

［4］赵克勤 .联系数及其应用 ［J］.吉林师范学院学报，1996，17（8）：50～53.

［5］王坚强 .几类信息不完全确定的多准则决策方法研究 ［J］.长沙：中南大学，2005.

［6］Deschrijver G，Kerre E.on the relationship between some extensions of fuzzy set theory ［J］.Fuzzy Sets and Systems，2003，133：227～235.

［7］Li Dengfeng.Multiattribute decision making models and methods using intuitionistic fuzzy sets ［J］.Journal of Computer and System Sciences，2004，70（1）：73～85.

［8］徐泽水 .不确定多属性决策方法及应用 ［M］.北京：清华大学出版社，2004：58～63.