《数学分析》中的分析与综合方法研究

邹健，宋述刚，陈忠 （长江大学信息与数学学院，湖北 荆州434023）

分析与综合是历史唯物主义与辩证唯物主义的基本思维方法之一，也是形式逻辑的方法之一［1］。按照哲学的观点，分析是把整体事物分解为各个部分、方面、阶段或要素，用相对静止、孤立的观点逐个加以研究的思维方法。分析即为化整为零。分析方法是多种多样的，有定性分析、定量分析、因果分析、结构分析、功能分析等。而综合则是在分析的基础上，将事物各个部分有机整合的思维方法。综合即为积零为整。这种整合，不是简单的、机械的部分相加，而是把思维对象的各个方面按其内在联系有机结合为一个统一的整体，从而把握事物的宏观本质的性质。

分析与综合虽然是2种不同的思维方法，但它们象一对孪生兄弟一样，形影相随，相互依赖，相互影响与转化。首先，分析是综合的前提和基础，没有系统、全面、科学的分析，就不可能有正确的综合。其次，分析离不开综合的指导，分析以综合为目的，综合是分析的完成。分析与综合的思维过程是从感性具体到思维抽象，再从思维抽象到客观具体的过程。一般的，前者多用分析法，后者多用综合法。

《数学分析》的主要内容是微积分理论，其创立者是英国科学家牛顿与德国科学家莱布尼兹［2，3］。微积分的创立是人类文明史上的一个里程碑，其理论在18、19世纪得到了极大的发展，形成了分析数学的基础理论，并在物理学、化学、天文学、生物学等自然科学与工程技术中有着广泛的重要应用。在大学非数学专业中，关于微积分的课程被称为《高等数学》，但在数学专业中，则称为《数学分析》，这表明《数学分析》更着重强调微积分的分析综合思想方法。

虽然微积分研究的对象是函数，但其研究的课题涉及到无穷的世界，包括无穷集合、无穷过程等，如实数集、无穷数列、无穷级数、数列极限、函数极限、函数的导数与积分等。在《数学分析》中，有穷与无穷是一对典型的相互对立统一的矛盾。有穷中包含着无穷，而无穷更是包含着有穷，它们在一定的条件之下可以相互转化。例如，有穷区间（0，1）包含了无穷多个点，无穷区间（0，＋∞）包含了无穷多个有穷区间；在变换y＝tanx之下，两者相互转化。

人类对无穷的认识，经历了一个艰难、漫长的过程。第1次数学危机（无理数危机）、第2次数学危机（无穷小量危机）、第3次数学危机（无穷集合悖论）都与对无穷的认识有关。无穷的世界千姿万态，充满了难以想象的奥秘。这是因为人的认识、思维过程乃至生命都是有限的。如何运用有限的思维过程去认识、把握无限的集合与变化过程？适当的方式就是化无穷为有穷、化复杂为简单，这就需要运用分析与综合方法。

下面，笔者以《数学分析》课程中极限和定积分这2个重要概念为例，探讨其中的分析与综合方法。

1 极限概念中的分析与综合方法

极限理论是《数学分析》的基础与工具，而数列极限又是极限论的基本概念。这里，笔者仅以数列极限的概念为例，探讨其中的分析与综合方法。考虑数列极限：

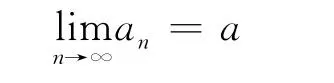
其定性的定义为：当n趋近于无穷大时，an无限趋近于a。如何寻求其定量的定义呢？事实上，an趋近于a是一个无穷的复杂过程，运用分析的方法，可以把它分解为各个变化阶段，如：

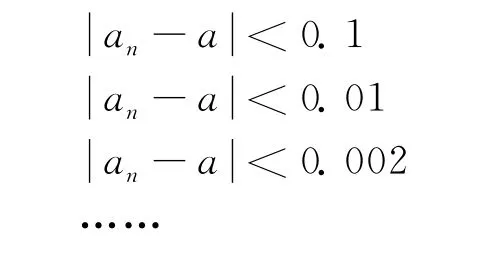
对于进入每个变化阶段，可以用相对静止、孤立的观点研究它们需要具备什么样的条件。以具体的极限＝0为例，要求：

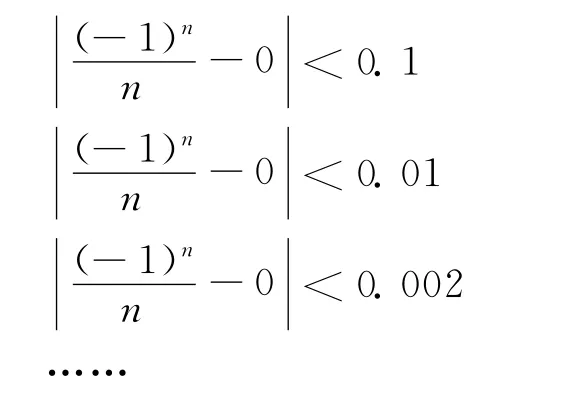
所得条件是自变量n必须分别大于某个正整数N＝10，N＝100，N＝500。这成为每个变化阶段所具备的共性，即可以综合为：对于给定的任意小的正数，总存在一个正整数，使得数列的项数大于这个正整数时，数列的变化进入相应的阶段。

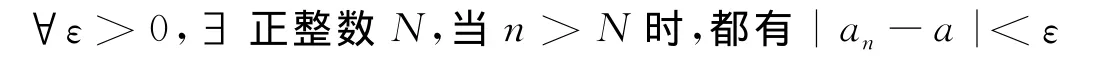
正是运用了分析与综合的方法，德国著名数学家魏尔斯特拉斯才首次给出了极限的现代定义。

运用同样的思维方法，可以得到函数极限的定义。以此为基础，又可定义函数连续的概念与导数的概念。

2 定积分概念中的分析与综合方法

首先，使用分析法，将曲边梯形用铅锤的直线分割成若干个小的窄曲边梯形，然后对每个小曲边梯形，用孤立、静止的观点处理，将其近似看着小矩形，即函数f（x）在每个小区间［xi－1，xi］上看作是不变的，其值可任取f（ξi），ξi∈ ［xi－1，xi］。于是第i个小曲边梯形面积近似值为f（ξi）Δxi（Δxi＝xi－xi－1）。

其次，使用综合法，将各小曲边梯形面积近似值相加，得到整个曲边梯形面积的近似值：

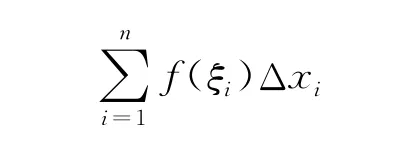
但这仅仅是一个近似值，需要有机整合。不难发现，随着分割越来越细密，和式（ξi）Δxi的近似程度就越高。因此，有机整合的手段就是让分割T越来越细密，当分割的细度 ‖T‖ →0时，和式的极限（如果存在的话）就是该曲边梯形的面积（精确值）。经过抽象概括，即得定积分的定义：

由此可知，在定积分的定义中，分割、近似即为分析过程，作和、取极限则为综合过程。可以说，定积分的定义是分析法与综合法相结合的完美范例。

运用同样的思维方法，可以定义重积分、曲线积分、曲面积分等概念。

3 结语

《数学分析》现已成为现代分析数学（包括函数论、泛函分析、微分方程等学科）的重要基础，因而学好该课程就显得尤为重要。由于大学与中学数学教学的差异与衔接等问题，导致相对一部分大学新生往往不能适应《数学分析》的学习，特别是感到基本概念难于理解，思维方式与表达形式不易掌握。因此，对《数学分析》课程中基本概念与思维方式教学的探讨就显得十分重要。极限、导数、积分等概念是《数学分析》中至关重要的基本概念，对它们的理解与掌握，是学好该课程的关键所在。而对这些概念的认识，又恰好是教学的重点与难点。由上所述，当了解了导入这些概念的分析与综合的思想方法以后，化解难点、突出重点就变得迎刃而解了。当然，除了上述探讨的分析与综合思维方法以外，《数学分析》中还蕴含客观世界普遍联系与运动、发展的观念，人类认识与实践的观念与规律，唯物辩证法的基本发展规律如质量互变规律、对立统一规律、否定之否定规律等等［4］。因此，在《数学分析》教学中，注重相关的哲学思想与方法，可以提升教师与学生双方的认识高度与水平，真正培养学生发现问题、分析问题、解决问题的能力，对指导《数学分析》及其相关后继课程的教学，提高教学质量，都有十分重要的意义。

［1］李秀林，王于，李怀春 .辩证唯物主义和历史唯物主义原理 ［M］.第5版，北京：中国人民大学出版社，2004.

［2］华东师大数学系 .数学分析 ［M］.第4版 .北京：高等教育出版社，2010.

［3］徐利治 .数学方法论选讲 ［M］.第3版 .武汉：华中科技大学出版社，2000.

［4］张景中 .数学哲学 ［M］.北京：北京师范大学出版社，2010.