笛卡尔乘积图K2×Cn及C3×Cn的符号边domatic数

李金强，朱智博，成纯波，姚萍萍，李向军 （长江大学信息与数学学院，湖北荆州434023）

记G＝（V（G），E（G））为一个图，V（G）和E（G）分别是G的顶点集和边集。若e∈E（G），用NG（e）表示G中与e相邻的边的集合，称为e的边邻域，称NG［e］＝NG（e）∪｛e｝为e的闭边邻域。当所指的图G很明确时，在记号中可以省略下标。Kn，Cn分别表示阶为n的完全图和圈。G×H表示G和H的笛卡尔乘积，其顶点集是V（G）×V（H），对x，y∈V（G），a，b∈V（H），（x，a）与（y，b）相邻当且仅当x＝y且ab∈E（H）或a＝b且xy∈E（G）。这里，笔者只考虑有限简单（无环，无平行边）无向图，未说明的符号和术语同文献［1］。文献［2］中引入了图的符号边控制数的概念。

定义1［2］设G是一个非空图，如果存在一个双值函数f：E（G）→｛1，－1｝，使得对任意e∈E（G）均有≥1成立，则称f为图G的一个符号边控制函数。图G的符号边控制数定义为：

domatic数通过控制集的数目来刻画。对V（G）的一个划分，若所有类都是一个控制集合，这个划分称为G的domatic划分，domatic划分的最大类数为domatic数［3］。Volkman L与Zelinka B［4］引入符号domatic数（ds（G）），是一个针对图顶点的符号控制概念，Li等［5］类似考虑针对边的符号控制问题，定义符号边domatic数。

定义2［5］G是一个非空图，G的符号边控制函数集合为｛f1，f2，…，fd｝，若满足对任意e∈E（G），≤1，则称为符号边控制集。图G的符号边domatic数为：

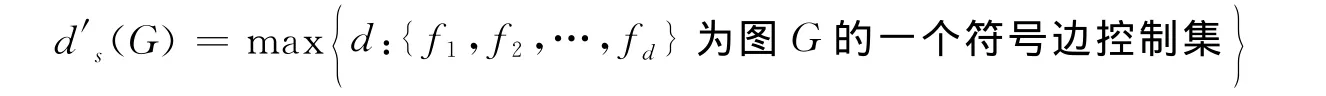
即G的最大符号边控制集含有符号边控制函数的个数为G的符号边domatic数。

对任意给定的图，确定其符号边domatic数是相当困难的，转而计算某些特殊图的符号边domatic数是很有价值的。Li等［5］确定了圈、星、扇、完全图及笛卡尔乘积图Pm×Pn的符号边domatic数。下面，笔者研究确定笛卡尔乘积图K2×Cn，C3×Cn的符号边domatic数。

引理1［5］图G的符号边domatic数是一个奇数。

引理2［5］若γ′s（G）为图G符号边控制数，ε（G）为图G边数，则d′s（G）γ′s（G）≤ε（G）。

引理3［5］令δ′（G）＝min，则d′s（G）≤δ′（G）。

1 笛卡尔乘积图K2×Cn的符号边domatic数

考虑图K2×Cn，其顶点可看作2×n点阵，记为 ｛xij：i∈ ｛0，1｝，j∈ ｛0，1，…，n－1｝｝。

定理1 对图K2×Cn，d′s（K2×Cn）为其符号边domatic数，则d′s（K2×Cn）≤3。

证明 设d＝d′s（K2×Cn），由于δ′（K2×Cn）＝min＝5，根据引理3可知d≤5。

假设d＝5，｛f1，f2，f3，…，fd｝为对应的符号边控制集，e0为任意边，则：

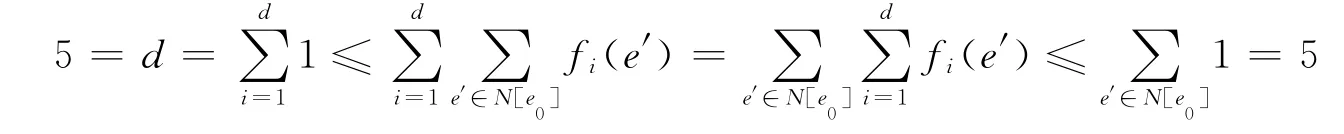
故任意边e0满足：

根据对称性，不妨设f（x0，0x0，1）＝－1。若要使＝1对边e0＝x0，0x0，1成立，则存在唯一e′∈N［e0］使得f（e′）＝－1，由对称性，考虑f（x0，1x1，1）＝－1，f（x0，1x0，2）＝－1这2种情况。

若f（x0，1x1，1）＝－ 1，则f（x0，1x0，2）＝f（x0，2x0，3）＝f（x0，2x1，2）＝f（x1，1，x1，2）＝1，令e0＝x0，2x1，2， 则与＝1相矛盾（见图1（a））。

若f（x0，1x0，2）＝－ 1， 则f（x0，1x1，1）＝f（x0，2x1，2）＝f（x1，0x1，1）＝f（x1，1，x1，2）＝1，令e0＝x1，1x1，2，则＝1相矛盾（见图1（b）），即证d≤4。

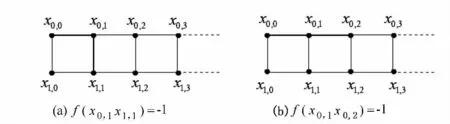
图1 定理1证明示意图

再结合引理1知，定理1得证。

下面用［a］表示不超过a的最大整数，［a］U表示不小于a的最小整数，脚标加法都为取modn的运算，示意图中粗边取值为－1，细边取值为1。

定理2 对任意正整数n≥3，d′s（K2×Cn）＝3。

证明 当n≥3时，令：

f1，f2，f3如图2所示，容易验证f1，f2，f3都是K2×Cn的符号边控制函数，且对任意e∈E（K2×Cn），（e）＝1，故 ｛f1，f2，f3｝是K2×Cn的符号边控制集，从而d′s（K2×Cn）≥3。结合定理1，可得d′s（K2×Cn）＝3。

2 笛卡尔乘积图C3×Cn的符号边domatic数

图2 K2×Cn符号边控制函数示意图（n为奇数）

考虑图C3×Cn，其顶点可看作3×n点阵，记为。第一脚标相同的点导出图为Cn，第二脚标相同的点导出图为C3。文献［6］中确定了C3×Cn的符号边控制数。

引理4［6］对于任意正整数n（n≥3），都有：

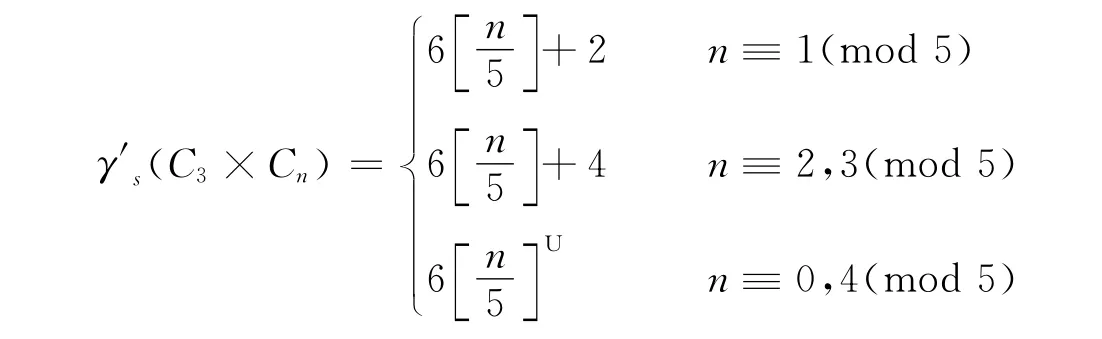
定理3 对任意正整数n（n≥3），都有：

证明 当n≡0（mod 5）时，对j＝0，1，2，…，；i＝1，2，3，4，5，令W（i，j）是C3×Cn中 以为顶点的K1，3子图，其中x1，5j＋i是W（i，j）的3度点。记：

是C3×Cn中的一条路。令E（i，j）＝E（W（i，j））∪E（P（i，j））。

根据引理2和引理4知，d′s（C3×Cn）≤5。对i＝1，2，3，4，5，令：

容易验证f1、f2、f3、f4、f5都是C3×Cn的符号边控制函数，且对任意e∈E（C3×Cn）＝1，故｛f1，f2，f3，f4，f5｝是C3×Cn的符号边控制集，故d′s（C3×Cn）＝5。

当n＝1，2，3，4（mod 5）时，根据引理4，结合引理2知，d′s（C3×Cn）≤3，对i＝1，2，3，令：

容易验证f1、f2、f3都是C3×Cn的符号边控制函数，且对任意e∈E（C3×Cn）＝1，故｛f1，f2，f3｝是C3×Cn的符号边控制集，故d′s（C3×Cn）＝3。

综上，定理3得证。

3 结语

研究确定了笛卡尔乘积图K2×Cn及C3×Cn的符号边domatic数，对任意正整数n≥3，图K2×Cn符号边domatic数d′s（K2×Cn）＝3，图C3×Cn符号边domatic数d′s（C3×Cn）＝。对一般的正整数m（m≥4），确定Cm×Cn符号边domatic数是值得进一步研究的问题。

［1］Bondy J A，Murty U S R.Graph theory with applications ［M］.London：Macmillan，1976.

［2］Xu B G.On signed edge domination numbers of graphs ［J］.Discrete Math，2001，239：179～198.

［3］Cockayne E J，Hedetniemi S T.Towards a theory of domination in graphs ［J］.Networks，1977，7：247～261.

［4］Volkmann L，Zelinka B.Signed domatic number of a graph ［J］.Discrete Applied Math，2005，150：261～267.

［5］Li X J，Xu J M.The signed edge－domatic number of a graph ［J］.Graphs and Combinatorics，2013，29（6）：1881～1890.

［6］李向军，袁旭东 .C3×Cn的符号边控制数 ［J］.广西师范大学学报（自然科学版），2006（1）：49～52.