空间相关MIMO信道下的OSTBC有限反馈预编码
2015-12-02
(杭州电子科技大学通信工程学院,浙江 杭州310018)
0 引 言
文献[1]提出了酉预编码的正交空时分组码(Orthogonal Space-Time Block Coding,OSTBC)有限反馈系统。基于此系统,文献[2]根据预编码设计准则[3]提出了新的预编码设计方案,具有更低误码率和快速选码特点。但上述码本的设计都是在信道为独立同分布情况下进行的。在实际多输入多输出(Multiple-Input Multiple-Output,MIMO)通信环境中,天线收发两端往往会有很大的相关性,针对空间相关MIMO信道,利用发送相关矩阵对独立同分布信道下的码本进行修正,所得码本具有不错的性能[4-5]。本文考虑酉预编码OSTBC有限反馈系统,首先推导了接收端信噪比(Signal to Noise Ratio,SNR)平均失真的上界,得到了预编码矩阵的结构,然后利用发送相关矩阵的平方根对码本进行旋转,设计了适用于空间相关MIMO信道下的新码本,同时设计一种快速选码方案。新码本不仅进一步提高了误码率性能,而且在快速选码方案下,选码复杂度有了很大的降低。
1 系统模型
酉预编码OSTBC有限反馈系统框图如图1所示。假设MIMO系统有Nr根接收天线,Nt根发射天线。H是有发送相关和接收相关的平坦衰落信道。相关模型采用Kronecker模型[6],表示为:

式中,Rt为发送相关矩阵,Rr为接收相关矩阵,G为独立同分布的复高斯随机变量矩阵。
预编码矩阵Pi是由接收端依据当前的信道实现而选出的最佳码字,并将码字序号i 反馈回发送端。假定波束矢量上等功率分配,那么与一个OSTBC 符号矩阵对应的接收信号可表示为:

式中,ρ为信噪比;X=[x1,x2,…,xT]是一个M×T 维的空时码矩阵,向量xt表示t时刻OSTBC编码器输出;W是Nr×T 维的噪声矩阵,其每一个元素均是零均值、单位方差的复高斯白噪声。
为了表述方便,本文将后面的数学符号进行说明。(·)H表示矩阵的共轭转置,表示绝对值,表示向量的Euclidean 范数,表示矩阵的Frobenius 范数。EH[·]表示对H的期望值,arg max(arg min)表示使表达式取得最大值(最小值)的任意变量,Ⅰk表示k×k的单位矩阵。
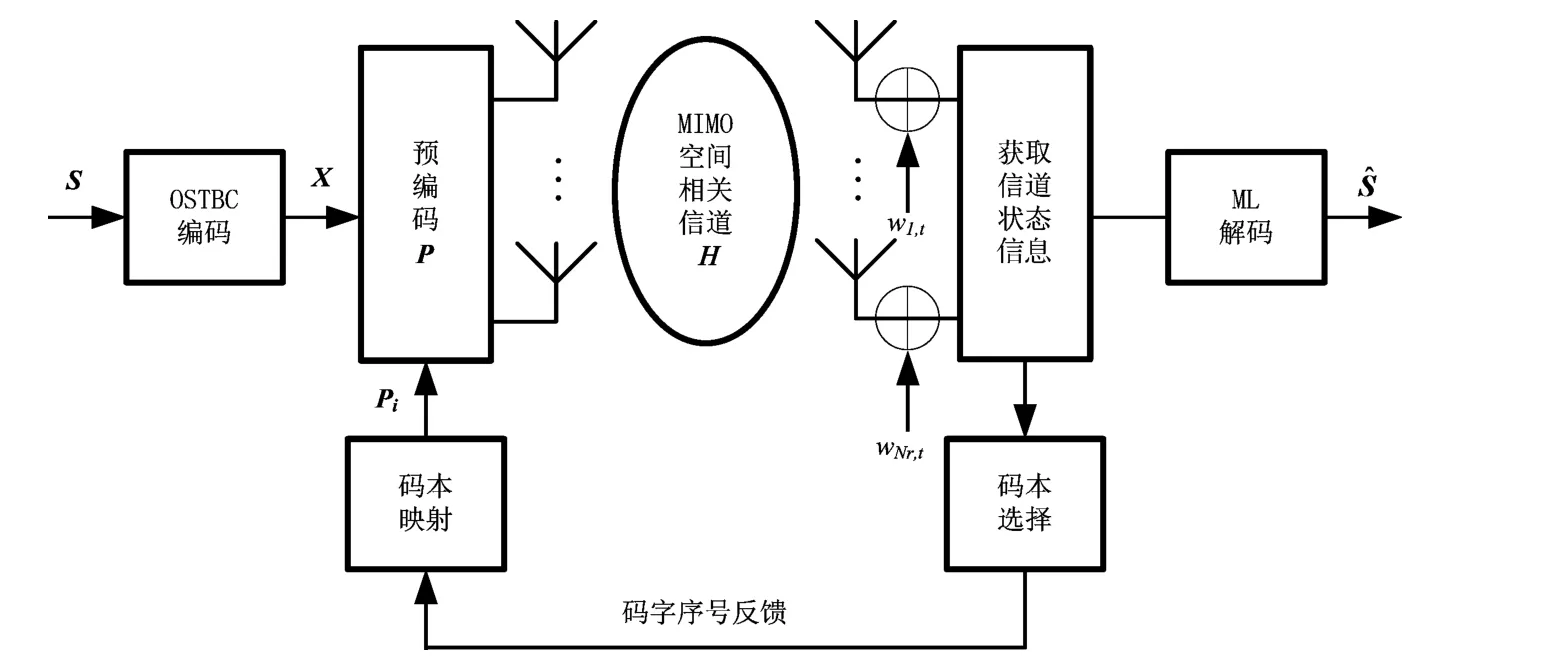
图1 酉预编码OSTBC有限反馈系统框图
2 空间相关信道下预编码的码本设计
2.1 多层码字的结构
文献[2]中的码本是为了最小化系统错误概率而设计的。它是把反馈比特分解成M个比特数,预编码矩阵是按列向量逐列地进行构造,形成具有M层结构的码字空间。假设系统接收端反馈r 比特,使得r=r1+r2+…+rM,令Jm=2rm(1≤m≤M),系统码本码字个数为J =2r。根据预编码设计准则,得到的J1个Nt维的复列向量v1,1,v1,2,…,v1,J1,将其作为第一层选码空间VJ1={v1,1,v1,2,…,v1,J1}。第二层选码空间为VJ2={v2,j1,1,v2,j1,2,…,v2,j1,J2}(1≤j1≤J1),其中每J2个向量都对应着上一层选码空间中的一个向量。应用预编码设计准则,直到得出第M层的选码空间VJM={vM,j1,j2,…,1,vM,j1,j2,…,2,…,vM,j1,j2,…,JM}(1≤j1≤J1,1≤j2≤J2,…)。通过最优选码或快速选码准则,在每一层选码空间中选出最优向量,然后组合成最优的预编码码字矩阵Fi(1≤i≤J)。
2.2 码本设计
文献[4]证明了当信道只有接收相关性,系统仍可用Grassmannian 码本进行预编码,但当信道还具有发送相关性,仍是本文需要解决的问题,下面考虑既有发送相关性又有接收相关性的情况。
通过最小符号错误概率准则得到的最佳预编码码字矩阵如下:

令m×n维矩阵A的奇异值分解[7]为:

式中,UA、QA、∑A分别是A的左奇异向量矩阵、右奇异向量矩阵、奇异值矩阵;k个非零奇异值以降序排列为σ1≥…≥σk,k为矩阵A的秩。文献[1]通过对H和P 实行奇异值分解,得到的上界为的前M列构成的矩阵,此时最优预编码矩阵为是QH前M列所构成的矩阵。
针对空间相关的MIMO信道,对于一个给定码本,定义一个平均失真函数:

为了最小化式(5),可以最小化式(5)的上界值。其上界值可由下式确定:
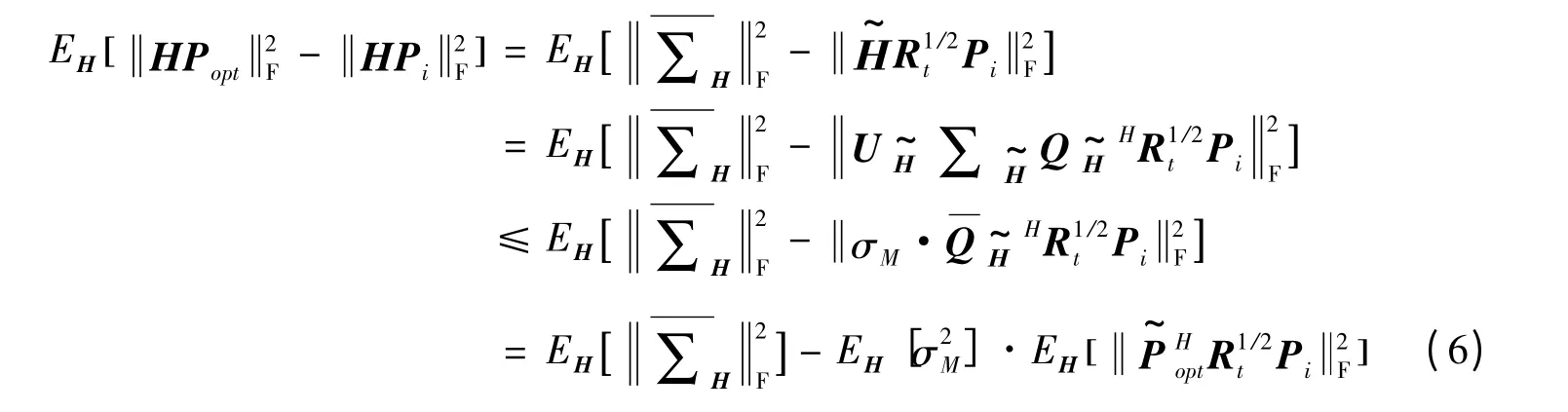
1)产生各层码字空间。如上节所述,生成适用于独立同分布瑞利衰落信道下各层码字空间,设在各层码字空间选择出来的列向量所组合成的码本F={F1,F2,…,FJ},码本包含J个码字;
3)码本量化。因为每个码字为酉矩阵,所以需要对每个码字进行酉矩阵化,使每个码字满足= ⅠM,最终得到新码本为P,P={P1,P2,…,PJ},其中
2.3 快速选码准则
接收端可根据式(3)确定出适合于当前信道实现的最佳预编码码字矩阵的序号,并将码字序号i 反馈回发送端。但这种选码准则计算量未免很大。因为码字是逐列地进行构造,所以预编码码字矩阵也可以逐列地进行选择,因此可以设计一种快速选码方案。

最佳码字矩阵中第二列向量下标i2为:

依此类推,直到得出最佳码字矩阵中的第M列向量的下标iM,经过上述M次下标确定后,可以直接得到最佳预编码码字矩阵。
3 仿真结果与分析
系统仿真参数为:H是3×4 维的空间相关的衰落信道,相关模型采用Kronecker模型,天线阵列为归一化线性阵列,发射天线间距离为dt=3λ,接收端天线间距离为dr=0.5λ,λ是载波波长。天线接收端到达角为0°,发送端和接收端的角度扩展分别为2°和60°。角度功率谱服从拉普拉斯分布。输入数据采用QPSK调制,OSTBC编码采用全速率的2×2 维Alamouti 编码。在不同反馈比特下,新码本和文献[2]码本在空间相关MIMO信道中的误码率性能曲线如图2、图3所示。

图2 反馈6 bit时不同码本误码率性能对比
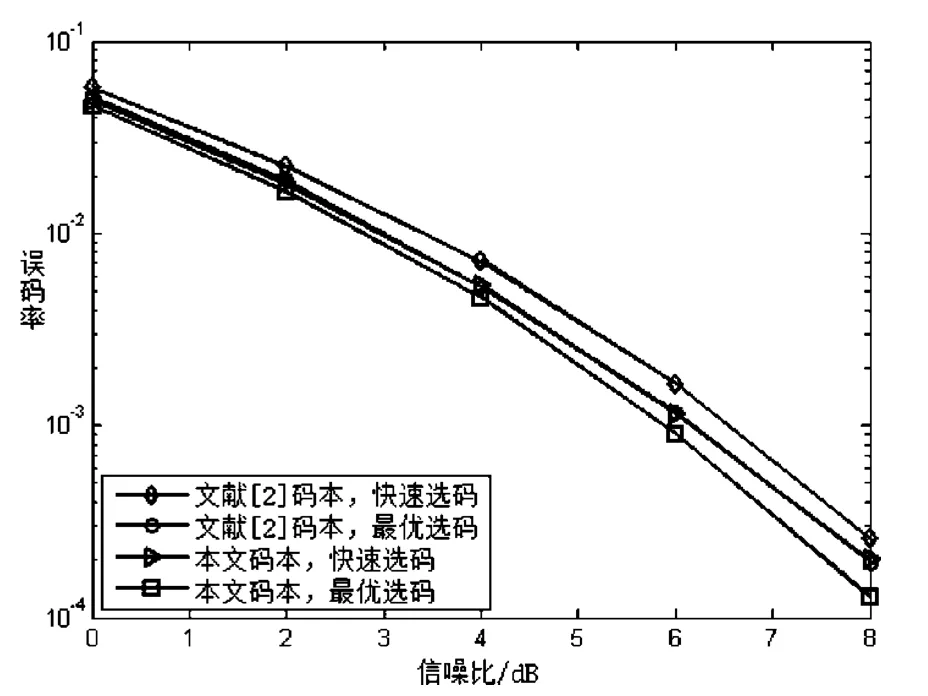
图3 反馈8 bit时不同码本误码率性能对比
在图2中,反馈比特r=6 且r=r1+r2=3+3。由图2可知,新码本在最优选码方案和快速选码方案下所表现出的性能都优于文献[2]中码本性能。在图3中,反馈比特r=8 且r=r1+r2=5+3,新码本在最优选码方案下的系统性能得到进一步的提升。
在图2中,针对一个具体信道实现H,为了选出最佳预编码码字矩阵,最优选码方案要对比26=64次,而快速选码方案只需要进行2次选择,每次需要对比23=8次,则一共只需进行16次选择,两者相差3倍。在图3中,最优选码方案要对比28=256次,而快速选码方案只需要进行2次选择,需要对比25=32和23=8次,则一共只需进行40次选择,两者相差5.4倍。很显然,最优选码方案需要计算J=J1×J2×·…×JM次矩阵HPi的Frobenius 范数,而快速选码方案只需要计算J1+J2+…+JM次两个向量的内积,因此系统在快速选码方案下,选码复杂度有了很大的降低。
图4描述了反馈6 bit时新码本在仅接收相关、仅发送相关、发送和接收同时相关信道下的误码率性能对比。在信道仅接收相关时,系统误码率性能优于仅发送相关、发送和接收同时相关这两种情况,而在信道仅发送相关时,系统误码率性能曲线与发送和接收同时相关情况下的基本重合,这也说明了前文所说的当信道只有接收相关性时系统仍可用原有码本进行预编码。
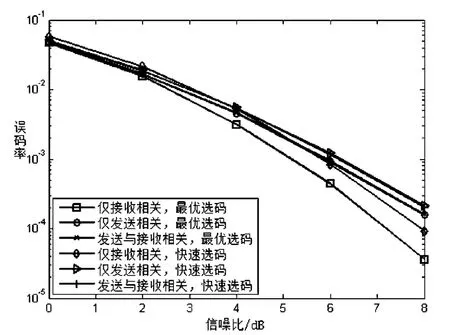
图4 信道在不同相关情况下新码本的性能对比
4 结束语
针对酉预编码OSTBC有限反馈系统,本文通过理论推导,得到了信道具有空间相关性时预编码矩阵的结构,利用发送相关矩阵对独立同分布信道下的酉预编码码本进行旋转操作,设计出适用于空间相关信道下的新码本。同时设计一种快速选码方案。此新码本不仅进一步提高了误码率性能,而且在快速选码方案下,选码复杂度有了很大的降低。
[1]Love D J,Heath R W.Limited feedback unitary precoding for orthogonal space-time block codes[J].IEEE Transactions on Signal Processing,2005,53(1):64-73.
[2]刘顺兰,刘艳艳,王海泉.基于OSTBC的有限反馈预编码设计[J].电路与系统学报,2013,18(1):443-448.
[3]Wang H Q,Zhao Z J.A MIMO system with finite-bit feedback based on fixed constellations [J].Science China Information Sciences,2013,56(6):1-14.
[4]Love D J,Heath R W.Grassmannian beamforming on correlated MIMO channels[J].Global Telecommunications Conference,2004.IEEE,2004:106-110.
[5]Xia P,Giannakis G B.Design and analysis of transmit-beamforming based on limited-rate feedback[J].IEEE Transactions on Signal Processing,2006,54(5):1 853-1 863.
[6]Pourahmadi V,Kohandani F,Mobasher A.On the accuracy of channel modeling based on the Kronecker product[J].
Vehicular Technology Conference Fall (VTC 2010-Fall),2010 IEEE 72nd,2010:1-5.
[7]张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004∶344-354.
