TiO2忆阻器的磁控模型分析及电路实现

刘　威，王光义

(杭州电子科技大学射频电路与系统教育部重点实验室，浙江 杭州 310018)

摘要：为了建立忆阻器的电导模型，基于TiO2忆阻器的荷控数学模型分析了其无源和有源的磁控数学模型，并设计了实现其伏安特性的双口电路模型，对电路模型进行了理论分析。利用Multisim对磁控忆阻器的电路模型进行了仿真验证，不同参数条件下的仿真结果与磁控忆阻器模型的特性完全一致。

关键词：忆阻器；磁控忆阻器；等效电路模型

DOI: 10.13954/j.cnki.hdu.2015.02.002

TiO2忆阻器的磁控模型分析及电路实现

刘威，王光义

(杭州电子科技大学射频电路与系统教育部重点实验室，浙江 杭州 310018)

摘要：为了建立忆阻器的电导模型，基于TiO2忆阻器的荷控数学模型分析了其无源和有源的磁控数学模型，并设计了实现其伏安特性的双口电路模型，对电路模型进行了理论分析。利用Multisim对磁控忆阻器的电路模型进行了仿真验证，不同参数条件下的仿真结果与磁控忆阻器模型的特性完全一致。

关键词：忆阻器；磁控忆阻器；等效电路模型

DOI:10.13954/j.cnki.hdu.2015.02.002

收稿日期：2014-08-29

基金项目：国家自然科学基金资助项目(61271064，60971046)；浙江省自然科学基金重点资助项目(LZ12F01001)；浙江省重点科技创新团队资助项目(2010R50010)

通信作者：

作者简介：刘威(1989-)，男，安徽阜阳人，在读研究生，非线性电路与智能信息处理.王光义教授，E-mail: wanggyi@163.com．

中图分类号：TN601

文献标识码：A

文章编号：1001-9146(2015)02-0005-04

Abstract:This paper aims at establishing the conductivity model of the memristor. On the basis of charge-controlled TiO2memristor， build the passive and positive flux-controlled mathematical model， through which two-port-circuit model is designed and verified by a theoretical analysis. Present a simulation and verification for the flux-controlled circuit model using Multisim and the results turn out to be exactly the same as characteristics of the flux-controlled memristor under different conditions．

0引言

2008年，HP实验室的Stanley Williams等在《Nature》上报导了一种新型的具有忆阻特性的纳米级固态元件，从而验证了1971年L.O.Chua提出的衔接磁通与电荷之间关系的第四种基本电路元件，即忆阻器的存在[1-2]。忆阻器是一种具有记忆性的无源非线性电阻，在非线性电路、非易失性存储器、神经网络等方面有着广阔的潜在应用前景[3]。文献[4]介绍了磁控忆阻器SPICE模型，文献[5]提出了一个具有光滑连续的三次单调上升的非线性函数的归一化磁控忆阻器。目前人们对忆阻器展开了一些初步研究，HP忆阻器至今也仅仅为使用忆阻器的存储芯片设计出发展架构，尚未被商业化，因此构建HP忆阻器的等效电路模型成为目前研究的关键。HP实验室提出的忆阻器模型实际上是荷控忆阻器模型，荷控忆阻器比较容易实现，但是在电路设计与应用中，尤其在研究忆阻器并联电路时，利用磁控记忆电导更为方便。因此，本文研究了磁控忆阻器的数学模型，设计了其等效电路，对数学和电路模型进行了理论分析和仿真验证，设计的电路模型可替代实际忆阻器进行实验和应用研究。

1忆阻器模型

1.1　HP忆阻器模型

L.O.Chua提出了电阻、电容和电感之外的第4种基本电路元件——忆阻器。忆阻器分为荷控与磁控两类，电荷q与磁通量φ之间的关系分别如下[1]：

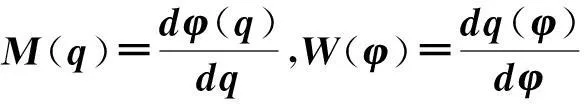
(1)

由式(1)，推导出忆阻器两端的电压和电流的基本关系为：

u(t)=M(q)i(t)，i(t)=W(φ)u(t)

(2)

式中，M(q)是记忆电阻，W(φ)是记忆电导。

2008年，HP实验室Strukov等证明了实际忆阻器的存在，并制作出纳米级的TiO2忆阻器[2]，其模型如图1所示，它由一片厚度为D的双层二氧化钛薄膜构成，左半部分是掺杂的，右半部分是非掺杂的，W是掺杂层的厚度。当两端施加不同方向的电压时，掺杂部分的离子漂移引起两层薄膜之间的边界发生移动，导致忆阻器的阻值发生变化。

图1　TiO2忆阻器模型

HP实验室对TiO2忆阻器的研究表明，其端口电压与电流有如下的关系式[2]：

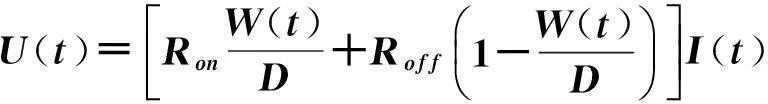
(3)

式中，Ron是W(t)=D时的忆阻器阻值，Roff是时的忆阻器阻值。

1.2　磁控忆阻器数学模型

电路设计中，通常是以电压源作为激励源，荷控型忆阻器的阻值是受流经自身电流大小控制的，使得荷控忆阻器在电流源激励下才表现出磁滞回环特性[4]。因此利用电路实现一个磁控型忆阻器模型具有十分重要的意义。

根据文献[6]磁控型忆阻器模型：

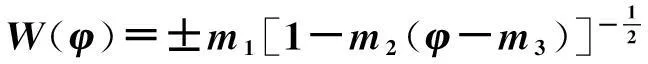
(4)

式中，m1=1/Roff，m2=2μvRon/RoffD2，m3=φ0，可以得到两个根，其中一个为正根，对应的是无源忆阻器，另外一个为负根，对应的是有源忆阻器。

2磁控忆阻器等效电路设计

根据对磁控型忆阻器理论模型的分析，采用T型电阻网络构建一个磁控型忆阻器模型。T型网络由3个电阻R1、R2、R3构成，R1、R2电阻的A、B两个端口作为忆阻器模型的二端口，R3电阻的一端口C点作为忆阻器AB端口电压的一个反馈信号接入点，磁控型忆阻器的完整电路如图2所示。采用的仪用差分放大器AD620AN标记为U1，采用的运算放大器LM324AD分别标记为U2，U3，U4，U5，U6，U7，U8。利用U1取忆阻器AB端口电压值并放大，U2，C1，R5构成积分运算电路，将U￣￣1的输出通过积分运算电路后得到UO2，由于积分后的结果UO2中含有直流分量，会影响后端的乘法器运算，因此在B点连接一个RC高通滤波器滤除直流。U3构成反相比例运算电路，U4起到反相的作用，U5与乘法器A1构成求根电路，U6与A2构成除法电路，U7与A3等构成反相比例运算电路，最后通过U8反馈到T型网络的端口C。

图2　磁控忆阻器电路原理图

对以上电路进行推导分析，利用仪用差分放大器取出忆阻器T型网络AB端口的差模信号，采用仪用差分放大器的高输入阻抗特性可以避免在取信号时对T型网络AB端口电压的干扰，R4为仪用差分放大器U1的外接电阻。则U1输出为：

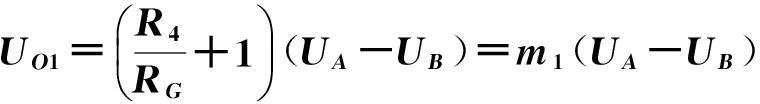
(5)

将仪用差分放大器U1输出电压UO1经过积分运算得到UO2：

(6)

UD≈m3UO2

(7)

通过比例运算电路将V1和UD输入到集成运放U3，反向后得到UO4，将乘法器A1的两个输入端接到集成运放U5的输出端构成求根运算电路，将其输出UO5作为乘法器A2构成的除法运算电路的输入，输出是UO6，再通过乘法器A3将信号UO6与UO1相乘得到输出：

(8)

通过U7构建的反相比例运算电路和U8反向电路求得：

(9)

对T型网络的O节点由基尔霍夫电流定律得到：

(10)

设R1=R2=R3，可得：

(11)

3磁控忆阻器的电路实现

激励源为幅度2 V的正弦电压信号时，在f=800 Hz、f=1 500 Hz频率下的Matlab与Multisim仿真实验结果分别如图3、图4所示。图3(a)为端口电压与端口电流的时域特性图，图3中幅度高者表示忆阻器端口电压UAB，幅度低者表示取忆阻器模型中R1两端的差模电压信号UR1，作为流经忆阻器的电流IAB，即UR1=IABR1。

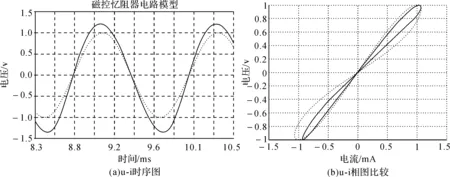
图3　f=800 Hz激励为正弦波时的仿真结果

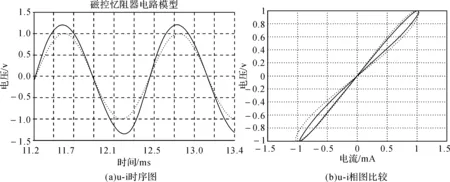
图4　f=1 500 Hz激励为正弦波时的仿真结果

图3(b)中虚线与图4(b)中虚线分别是输入信号频率f=800 Hz与输入信号频率f=1 500 Hz下的u-i相图，表明频率越大，磁滞回环曲线向内收缩。同时，Multisim仿真结果图3(b)与图4(b)中实线相比较也是呈现磁滞回环曲线向内收缩，在相同频率下Matlab仿真结果与Multisim仿真结果基本重合，表明等效电路模型的精度比较好。

4结束语

本文基于HP实验室的TiO2忆阻器数学模型，建立了磁控的忆阻器数学模型及其等效电路，通过电路仿真观察忆阻器在不同频率信号激励下的滞回伏安特性，验证了方案的正确性。本模型可替代实际忆阻器进行应用于忆阻器的基本特性研究与应用电路的分析和设计之中。

参考文献

[1]Chua L O. Memristor-the missing circuit element[J]. Circuit Theory， IEEE Transactions on，1971，18(5)：507-519．

[2]Strukov D B， Snider G S， Stewart D R， et al. The missing memristor found [J]. Nature，2008，453(7 191):80-83．

[3]王小平，沈轶，吴计生，孙军伟，等.忆阻及其应用研究综述[J].自动化学报，2013，39(8)：1 170-1 184．

[4]Batas D， Fiedler H. A Memristor SPICE Implementation and a New Approach for Magnetic Flux-Controlled Memristor Modeling[J]. IEEE Transactions on Nanotechnology，2011，10(2)：250-255．

[5]包伯成，胡文，许建平，等.忆阻混沌电路的分析与实现[J].物理学报，2011，60(12)：58-65．

[6]Wang G Y， He J L， Yuan F， et al. Dynamical Behaviors of a TiO2 Memristor Oscillator[J]. Chinese Physics Letters，2013，30(11)，110 506．

Flux-controlled Model Analysis and

Circuit Implementation of TiO2Memristor

Liu Wei， Wang Guangyi

(KeyLab.ofRFCircuitandSystem，MinistryofEducation，HangzhouDianziUniversity，HangzhouZhejiang310018，China)

Key words: memristor; flux-controlled memristor; equivalent circuit model