外加应力作用下Ni75Al11.5V13.5合金时效沉淀相的定向粗化

曾 霞，杨晓平，刘 磊

(1.陕西国防工业职业技术学院，西安 710300;2.西北工业大学材料学院，西安 710072)

固态相变由于沉淀相与母相间的晶格失配导致弹性应变能升高，且外加应力也导致系统产生均匀外加应力从而改变系统的弹性能，而系统中的弹性能显著影响时效沉淀生长和粗化行为［1］.在外加应力场作用下，晶格失配沉淀优先在外加应力方向的粗化称定向粗化［2］，或称筏化.对弹性均匀系统，KHACHATURYAN［2］就合金相变过程中晶格失配应变能对合金沉淀行为的影响进行了详细的论述.VERON等对Ni基合金的定向粗化行为进行了研究［3］.已有很多方法研究弹性应力作用下定向粗化类型的决定因素，如基于能量方法研究在外加应力作用下单一颗粒的沉淀过程能量最小化对颗粒形态和位向的影响［4］;采用热力学研究方法研究在应力作用下失配不均匀颗粒周围化学势的瞬态分布［3］;动力学研究方法则基于嵌入原子法［5］和连续相场方法［6－7］.上述研究方法在介观尺度研究定向粗化颗粒的形态以及影响定向粗化因素方面有效，但无法揭示定向粗化过程沉淀和母相结构以及原子配置，尤其是在有序结构间的反相畴界和点缺陷等方面上述方法无效，而微观相场在这方面具有优势.PODURI等［8］利用微观相场研究了Ni－Al－V合金的时效行为，但未考虑由于母相与沉淀相间由于结构差异引起的晶格适配导致的晶格适配应变能，以及沉淀相在外加应力作用下的定向粗化行为.

本文将 KHACHATURYAN［2］的微观弹性理论扩展到微观相场模型中，并利用该模型模拟Ni基Ni75Al11.5V13.5合金在外加应力作用下L12结构的γ'(Ni3Al)相和D022结构Ni3V相沉淀相的定向粗化行为.

1 计算模型

本文在 PODURI［8］基础上，发展了外加应力作用下三元合金微观相场沉淀演化动力学模型.在该模型中，原子配置和相的形态由原子占位概率函数Φα(r，t)表示，其意义为某一时刻在空间的某一点r找到α溶质原子的概率.在高温下，三元系统平衡态是均匀的无序状态，将一定溶质浓度的均匀无序系统降到低温时效，系统因为原子的有序化或簇聚而失稳.在时效温度，系统从初始的不稳定态向稳定态的演化是一个高度非线性的复杂过程.KHACHATURYAN［9］等发展了一种 Onsager型微观扩散方程来描述该过程.空间点r处的溶质原子占位概率Φα(r，t)满足动态方程

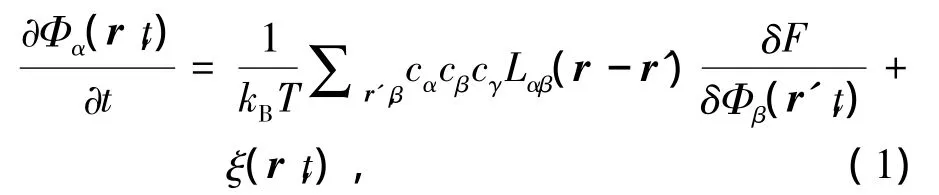
式中:kB是 Boltzmann 常数;T 是温度;Lαβ(r－r)是r处的原子与r'处的原子对在单位时间内交换概率;F是系统的总Helmholtz自由能;ξ(r，t)是系统外加成分起伏以利于新相形核，成分起伏项ξ(r，t)是期望为0 的高斯随机分布，满足〈ξ(r，t)〉=0，且

在平均场近似下，离散格点二元系统的总自由能F可以表示为

其中

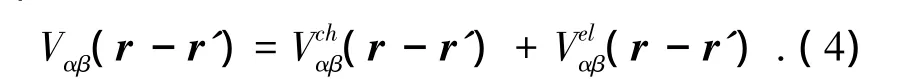
式中:Vch(r－r')为无畸变晶格中r点原子与r'原子间的化学交互作用能;Vel(r－r')为有畸变晶格r点原子与r'点原子间的弹性交互作用能.化学交互作用能

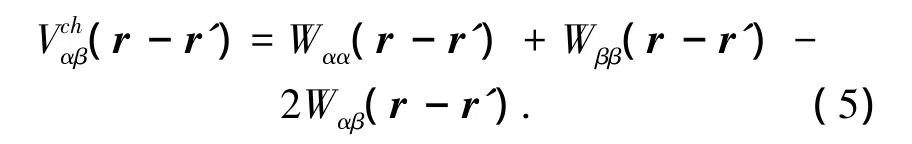
其中，Wαβ(r－r')是无畸变晶格位置 r和r'的α、β原子对间的两两相互作用能.立方结构的母相的弹性常数由 KHACHATUYRAN［9］的微观弹性理论，可以写出沉淀颗粒的嵌入对三元系统总弹性能的贡献.

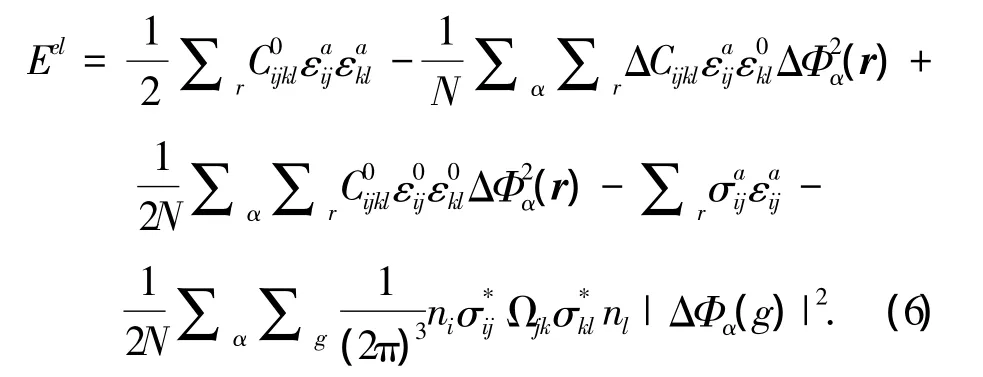
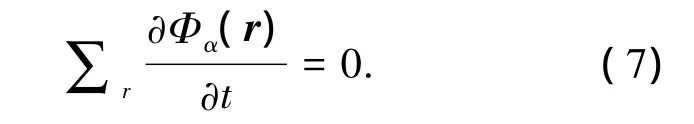
将式(4)、式(7)代入式(1)得到三元体系微观相场方程组，对方程组中的每个方程进行Fourier变换，得到倒易空间微观相场动力学方程

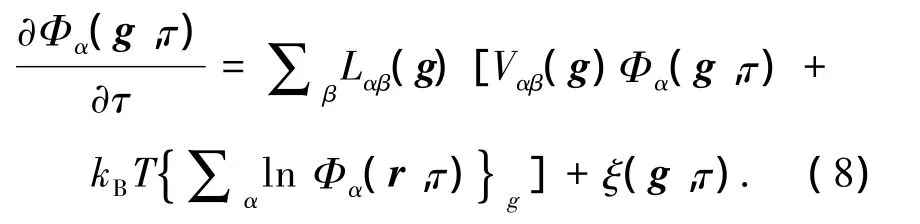
式中 τ =cαcβcγt/(kBT)为无量纲化的时间，这里cα(r，t)、cβ(r，t)是系统中任意平衡浓度，为了计算的方便，这里用合金浓度代替.是相应实空间变量的Fourier变换.而Vch(g)可以展开为临近晶格原子间的相互作用能叠加，

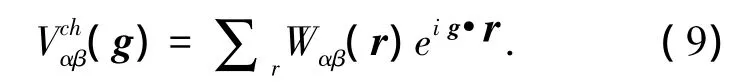
假设原子只在最临近格点间跳跃，由于系统总原子数守恒，对于 f.c.c 晶格，

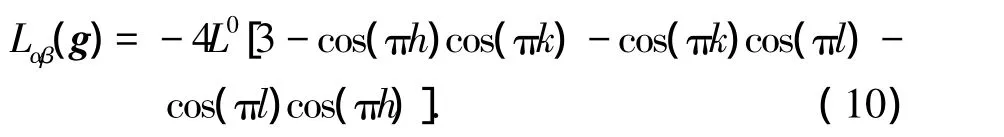
其中L0与最临近的原子对间单位时间内跃迁的概率成正比［3］.

上述过程是在三维空间进行的，对于二维空间只需令z=0即可.立方晶格在(001)面上进行二维投影得到的是四方晶格，该四方晶格的晶格常数是面心立方的一半.即二维四方晶格的单位格矢与面心立方晶格单位格矢满足

式中:a1、a2是面心立方晶格的单位格矢;b1、b2是该面心立方晶格二维投影面上四方晶格的单位格矢.相应的四方晶格在倒易空间的格矢满足

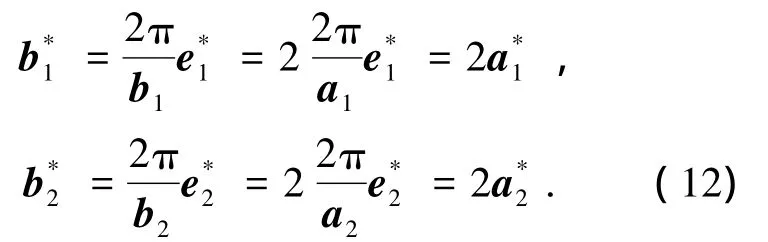
式中:b*1、b*2是四方晶格的倒易单位格矢;a*1、a*2是相应立方晶格的倒易单位格矢.L12相和D022的晶体结构参数列于如表1所示，其中Ni3V的弹性常数为第一性原理计算得到.

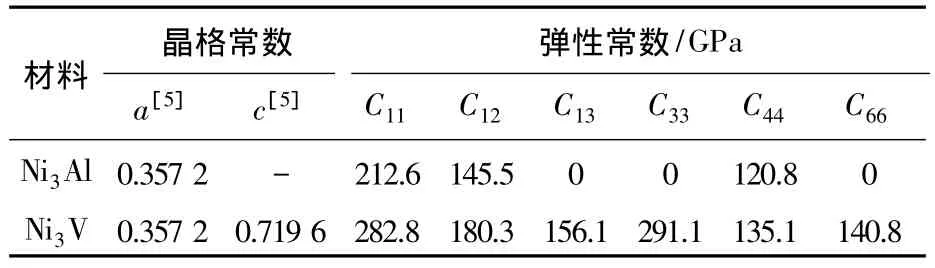
表1 Ni3Al和Ni3V的弹性常数

2 外加应力作用下γ'相沉淀的定向粗化

在外加应力σaij作用下，系统中产生均匀的外加应力 εaij，将外加应力 εaij施加于系统，可以模拟外加应力σaij作用下合金的沉淀行为.在外加应力场作用下，颗粒除了受上述的扩散、畸变能和反相畴界三者作用外，还受到外加应力场引入的应变能的作用.外加应力场作用下单一颗粒和多颗粒的形态演化都与没有外加应力场存在明显差异.

图1是微观相场场模拟Ni75Al11.5V13.5合金于1 046.5 K等温时效过程中，在［100］方向对合金持续施加σaxx=200 MPa拉应力，得到的γ'沉淀相定向粗化形态，计算区域为0.363 μm×0.363 μm.图1(c)是外力场微观相场模型模拟Ni75Al11.5V13.5合金在［100］方向持续施加σaxx=200 MPa拉应力作用下 1 046.5 K等温时效 28.6 h γ'沉淀相形态，可以看出，颗粒被外加拉应力拉长的同时，所有颗粒沿［100］方向分布.沉淀颗粒在哪个方向被拉长与沉淀、母相的弹性常数有关，也与沉淀相、母相弹性各向异性有关［10］.在沉淀的总弹性能表达式(6)中，与沉淀形态有关的项称有效应变能(Eema)为

其中σ*ij称有效应力.由有效应力可以得到有效应变 ε*ij，

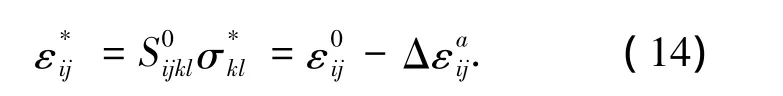
为有效外加应力.有效应变是在外加应力的激励下，系统可能产生的应变的一级近似［9］.在系统最小应变能的要求下，沉淀将沿应变能最小的方向生长.

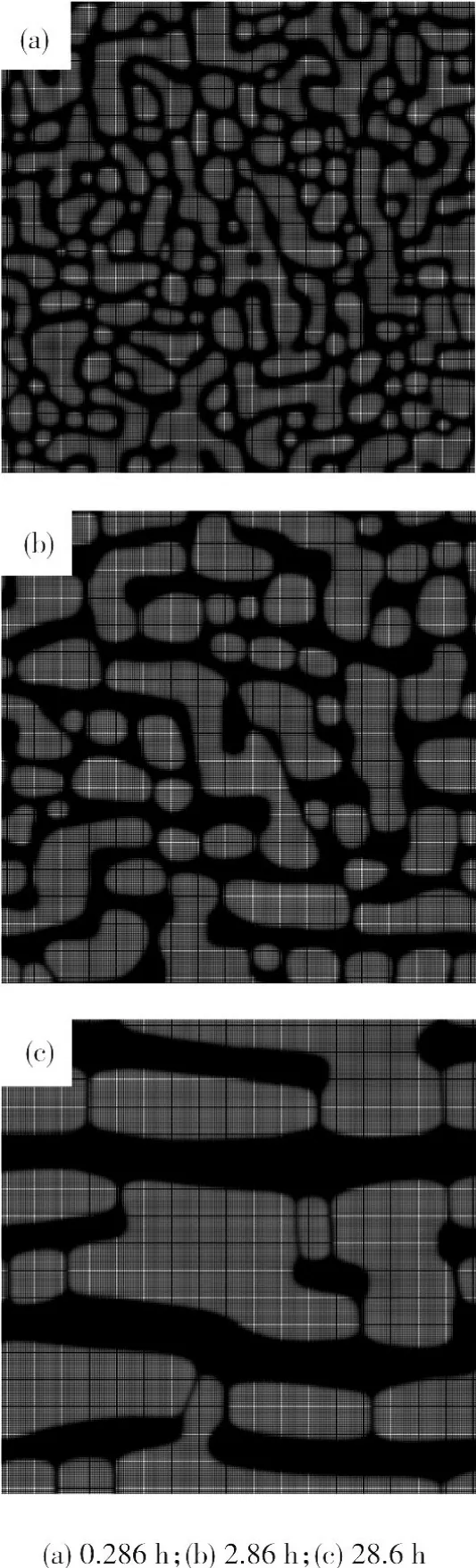
图1 微观相场模拟的L12沉淀形态

可用有效应力来分析外加应力场对颗粒形态的影响.对Ni75Al11.5V13.5合金时效过程析出 γ'相的情况，由于沉淀与母相的弹性常数相差不大，可以用母相的弹性常数代替平均弹性常数，由此得，由式(13)可以导出沉淀沿{1 00 }面生长时 Eel取最小值［9］.在外加拉应力的作用下，如沿［100］方向外加一个拉应力σaij，该拉应力将在沉淀界面上产生应变εaij，沉淀在拉应力的作用下沿［100］方向拉伸而在［010］和［001］方向上Poisson压缩，因此，有 εaxx＞0 和εayy=εazz＜0.

对于Ni75Al11.5V13.5，由表1可知沉淀相 γ'与母相 γ 弹性常数差 ΔCijkl＞0，由式(15)有 ε*xx＜ε*yy=ε*zz，因此，问题简化为矩形沉淀形状如何优化.根据 PRIKHODKO［11］的结论，如果 C011－C022－2C044＜0且0＜t=ε*xx/ε*yy＜1，则最小应变能约束将促使沉淀生长为(010)和(001)面上的碟形沉淀，即沉淀将在［100］方向被拉长.相反，如果在［100］方向施加压应力，最小应变能的约束将促使沉淀生长为(010)面上的碟形沉淀.图2(a)是连续相场模拟γ'相沉淀定向粗化结果;图2(b)是实验发现的L12结构沉淀相的定向粗化形态.将微观相场、连续相场与实验比较发现，相场方法模拟的γ'相定向粗化颗粒形态与实验得到的γ'沉淀相形态以及理论分析结果相符［10－12］.

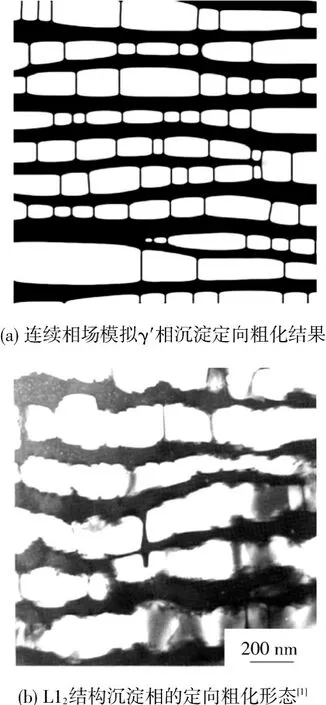
图2 连续相场模拟和实验观察到的γ'相的定向粗化形态

3 外加应力作用下D022相沉淀的定向粗化

在外加应力情况下，沉淀相D022首先在L12相与母相的相界面形核，图3(a)是沉淀时效2.86 h的形貌，晶核在{100}面呈层片状分布，这是由于在两相的相界面上满足D022形核所需的条件.

图3是Ni75Al11.5V13.5合金 1 046.5 K等温，在［100］方向施加σaxx=200 MPa拉应力，D022沉淀形态，计算区域为0.363 μm×0.363 μm，其中浅色为D022相，深色为L12相，与图1颜色互补.对于Ni75Al11.5V13.5合金1 046.5 K下等温时效，L12沉淀体积分数约为50%，两种沉淀相没有体积的优势，尽管如此，两项的形态仍有所不同.图3(b)是Ni75Al11.5V13.5在 1 046.5 K 时效28.6 h D022和L12两相的形态分布情况.由图3(c)可以看出，以反向畴界分隔的A、B区D022相的c轴转向拉伸方向，从而可以判断在定向粗化状态下，合金力学性能会出现一定的各向异性.

图3 微观相场模拟的D022沉淀形态

图4是 Ni75Al11.5V13.5在 1 046.5 K下拉伸28.6 h，不同的拉应力对沉淀定向粗化的影响.为了定量研究在同一温度下时效相同时间不同拉应力对沉淀定向粗化的影响，可以用不同应力作用下沉淀颗粒的长、宽比(p)来表示这种影响的强度.在1 046.5 K下等温时效，Ni75Al11.5V13.5在不同拉应力下时效相同的时间28.6 h，不同拉应力下长、宽比p的变化用图4所示.图4(a)表示L12颗粒长、宽比，图4(b)表示D022颗粒长、宽比，其中ξ=σxx/σ0xx，且 σaxx=200 MPa.可见外加应力大小对Ni75Al11.5V13.5沉淀定向粗化行为有显著影响.

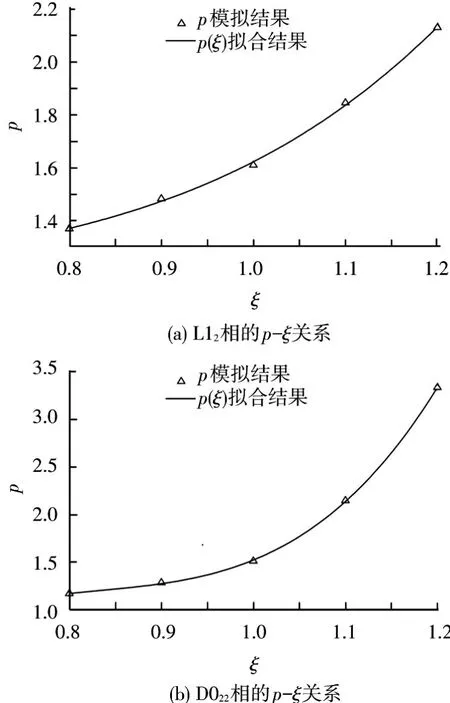
图4 拉应力对沉淀粗化的影响

4 结论

1)微观相场模型在原子尺度可以模拟相结构和晶格中的原子配置，并能清晰模拟有序相沉淀颗粒间的界面.

2)在外加应力作用下，γ'相的定向粗化行为与外加应力大小和方向以及持续施加的时间对γ'沉淀时效行为有显著影响.施加的外加应力越大、持续时间越长，外加应力方向的定向粗化效应越明显.

3)时效过程中D022在L12与母相界面形核，因此，D022相总是在L12相的夹缝中生长，其形态始终受L12相的制约而与L12相协调生长.

4)在外加应力作用下，D022的c轴转向外力的拉伸轴，由此可以推断Ni75Al11.5V13.5在定向粗化状态下力学性能呈各向异性.

［1］ PARIS O，FAHRMANN M，et al.A thermokinetic description of nanoscale grain grouth:Analysis of the activation energy effect［J］.Acta materialia，1997，45(3):1085－1097.

［2］ KHACHATURYAN A G.Theory of Structural Transformations in Solids［M］.New York:Wiley，1986.

［3］ VERON M，BRECHET Y，LOUCHET F.Strain induced directional coarsening in Ni based superalloys［J］.Scripta materialia，1996，34(12):1883－1886.

［4］ BERNARD FEDELICH，ALEXANDER EPISHIN，at al.Experimentalcharacterization and mechanical modeling of creep induced rafting in superalloys［J］.Computational Materials Science，2012，64:2－6.

［5］ CAHN J W，LARCHE F.A simple model for coherent equilibrium［J］.Acta matallurgica，1984，32(11):1915－1923.

［6］ LEE J A.Accumulation of radiation damage in plutonium［J］.Cryogenics，1962，2(3):183－184.

［7］ LI D Y ，CHEN L Q.Shape evolution and splitting of coherent particles under applied stresses［J］.Acta materialia，1999，47(1):247－257.

［8］ PODURI R，CHEN L Q.Computer simulation of atomic ordering and compositional clustering in the pseudobinary Ni-based system［J］.Acta mater，1998，46(5):1719－1729.

［9］ KHACHATURYAN A G，SEMENOVSKAYA S，TSAKALAKOS T.Elastic strain energy of inhomogeneous solids［J］.Physical review B，1995，52(22):15909－15919.

［10］ PRIKHODKO S V，ARDELL A J.Coarsening of γ'in Ni－ Al alloys aged under uniaxial compression:I.Early-stage kinetics［J］.Acta Mater，2003，51(17):5001－5012.

［11］ ARDELL A J，PRIKHODKO S V.Coarsening of γ'in Ni－ Al alloys aged under uniaxial compression:II.Diffusion under stress and retardation of coarsening kinetics［J］.Acta Mater，2003，51(17):5013－5019.

［12］ PRIKHODKO S V，ARDELL A J.Coarsening of γ'in Ni－ Al alloys aged under uniaxial compression:III.Characterization of the Morphology［J］.Acta Mater，2003，51(17):5021－5036.