分段平移相渗曲线方法校准网格粗化效果

张继成，闫志明，范佳乐，包智魁

（东北石油大学石油工程学院，黑龙江大庆163318）

油藏模拟网格粗化就是把细网格模型粗化成一个等效的粗网格模型，保持两个模型系统的油藏物性与渗流特征尽可能相同[1⁃3]。Mansoori将油藏模型网格粗化的方法划分为数值计算法、统计分析法和矢量法三大类[4]。D.C.Li[5]将油藏模型网格粗化的方法划分为单相流和多相流两大类，17种方法，而Cristie的分类是五大类。王家华等[6]利用渗透率粗化算法的线性相关系数和相对偏差对比的散点图分析粗化算法的误差。何吉祥[7]将误差分析方法划分为3种：平均累计误差分析、单点误差分析、Sablok误差计算方法分析。代曙光[8]将误差分析方法划分为相对误差、相对误差绝对值及平均累计3种。M.Murugesu[9]将粗化方法分为解析(静态)方法和数值(动态)方法。权勃等[10⁃11]通过小尺度等效表征技术提高了单井历史拟合精度及井间剩余油分布预测精度。目前的粗化方法一般都是在地质方面的油藏物性上尽量满足粗化前和粗化后的一致性，并没有在开发效果上达到完全一致，本文对粗化后的相渗曲线进行修改，最终达到粗化后和粗化前的开发效果一致[12⁃14]。

1 问题的提出

1.1 网格粗化的必要性

由于油藏的非均质性，油藏模拟网格粗化既要考虑满足油藏数模软件对网格数的处理能力，又要尽可能地保留原细网格模型的重要地质特征。对于可相加性的物性参数，如孔隙度、饱和度等，可采用算数平均法，其标准差将随样本数的增大而减小。因此，在油藏模拟粗化中，关键问题是如何处理不可相加性的物性参数——相对渗透率。

目前的网格粗化研究都是围绕着渗透率等地层属性参数展开研究，其目的是如何在地质上实现粗化后与粗化前的等效，但忽略了开发效果的等效问题。在网格粗化过程中，最终的目的是达到能够准确地预测油田开发效果。因此，有必要对粗化前后的模型进行开发效果对比，分析粗化过程中导致开发效果变化的原因，从而进行调整，最终得到最优的粗化方法。

1.2 网格粗化中存在的问题

根据油田的实际情况，利用Eclipse数值模拟软件，建立概念模型，模型为三层，原油黏度为12.2 mPa⋅s，地层中水的黏度为0.6 mPa⋅s，原始地层压力为10 MPa，含水饱和度为0.3，采用非平衡启动进行计算。网格粗化前，采用调和平均和算数平均计算方法，得到每层的平均渗透率分别为9.28、18.60、37.10、34.30、68.60、137.24 mD，纵向上呈正韵律分布，调和平均法如式（1）所示：

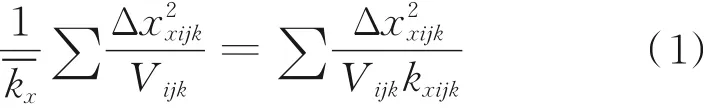
算数平均法如式（2）所示：

网格数量为16×16×3的模型经过粗化变为网格数量为4×4×3的模型，粗化前和粗化后概念模型如图1所示。

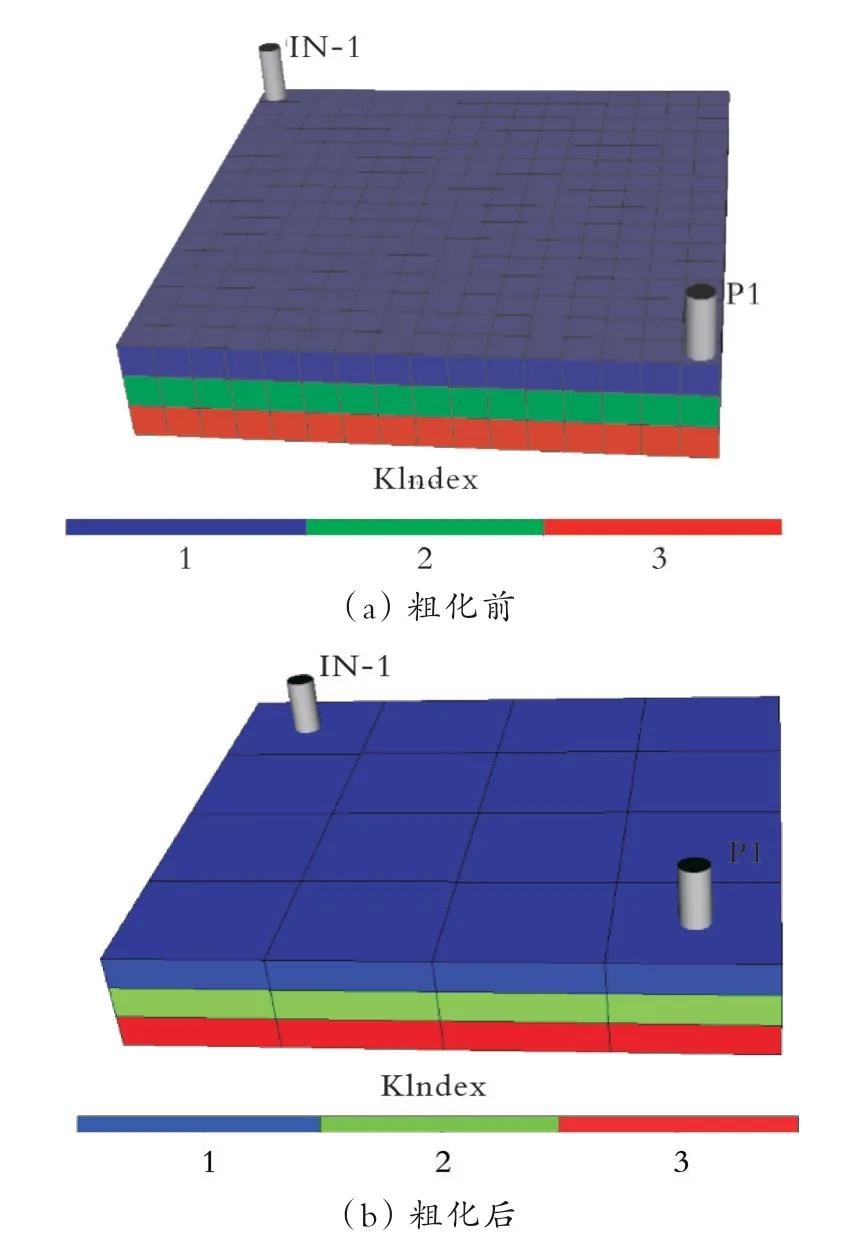
图1 粗化前与粗化后概念模型示意Fig.1 Schematic diagram of conceptual model before and after upscaling

粗化前和粗化后油水井设置相同的工作制度，水井以50 m3/d定注入量注入，油井以50 m3/d定产液量生产，保持注采平衡，设置生产年限为20 a，最终得到粗化前和粗化后含水率与采出程度的变化曲线，如图2所示。

图2 调和平均法和算术平均法粗化前含水率与采出程度关系Fig.2 The relationship between water cut and recovery degree before upscaling by harmonic average and aritmetic average

由图2可知，无论采用调和平均法还是算术平均法，粗化前与粗化后曲线存在明显差异，粗化后的含水率明显上升较快，采出程度相对较低，主要原因是网格步长增大后，水驱前缘变化较快，使油藏含水率增大较快，产水量增大，油藏中剩余油增大，导致采出程度降低。

2 水油比与采出程度关系式与相渗曲线的关系推导

水驱油田油、水相对渗透率比值可以比较简便地表达成饱和度的函数，方法是处理成幂指数的关系[11⁃12]，即从油、水相对渗透率（Kro/Krw）与含水饱和度（Sw）关系曲线中读出油相相对渗透率和水相相对渗透率的值，计算其比值及相应的含水饱和度，并绘制在半对数坐标轴上，结果如图3所示，该曲线的主体是直线，两端发生弯曲，直线段的表达式为：

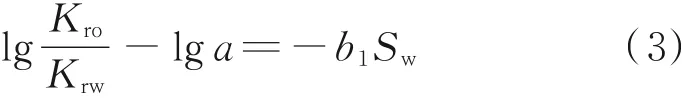
式中，Kro为油相相对渗透率；Krw为水相相对渗透率；Sw为含水饱和度；a为直线段延长线在纵坐标轴上的截距；b1为直线段的斜率。

图3 Kro/Krw与Sw的关系Fig.3 The relationship curve between Kro/Krw and Sw

整理式（3）得：

根据达西定律，油和水渗过岩石断面的流量分别为：

式中，qo为产油量，m3/d；K为岩石绝对渗透率，mD；qw为产水量，m3/d；μo为油相黏度，mPa⋅s；μw为水相黏度，mPa⋅s；A为渗流面积，m2；dp/dx为压力梯度，MPa/m。

含水率fw可写成：

将式（4）代入式（7）整理得：

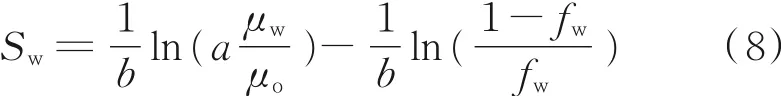
采出程度R可写为：

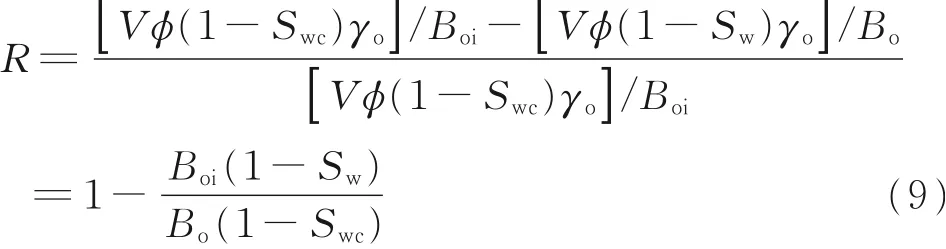
式中，V为岩石总体积；φ为孔隙度；γo为原油相对密度；Boi为原始原油体积系数；Bo为原油在地层压力p下的体积系数；Swc为束缚水饱和度。

将式（8）代入式（9）整理得：

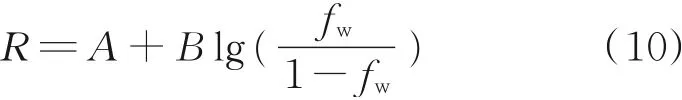
其中，

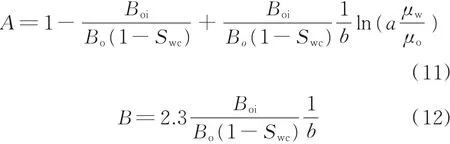
3 相渗曲线修改方法

3.1 计算粗化后油水相对渗透率的比值

算术平均方法计算水油比与采出程度之间的关系如图4所示，其粗化后与粗化前均为两条直线。

图4 16×16×3概念模型粗化前、粗化后和含水饱和度+0.01后水油比与采出程度关系Fig.4 The relationship curve between water oil ratio and recovery degree before and after upscaling of 16×16×3 conceptual model

对粗化前和粗化后的水油比与采出程度的关系曲线进行拟合，得到其对应线性方程的斜率和截距，如表1所示。

表1 粗化前与粗化后拟合曲线参数Table1 Fitting curve parameter tables before and after upscaling

表1 中，A粗化前、A粗化后分别为粗化前、粗化后采出程度与水油关系曲线截距；B粗化前、B粗化后分别为粗化前、粗化后采出程度与水油关系曲线斜率。

由于水油比与采出程度关系曲线与Kro/Krw与Sw的关系曲线存在一定的关系，根据式（11）、（12）将粗化前与粗化后的关系式进行联立并代入表1中的相关参数可以得出粗化后的相对渗透率曲线，其具体推导过程为：

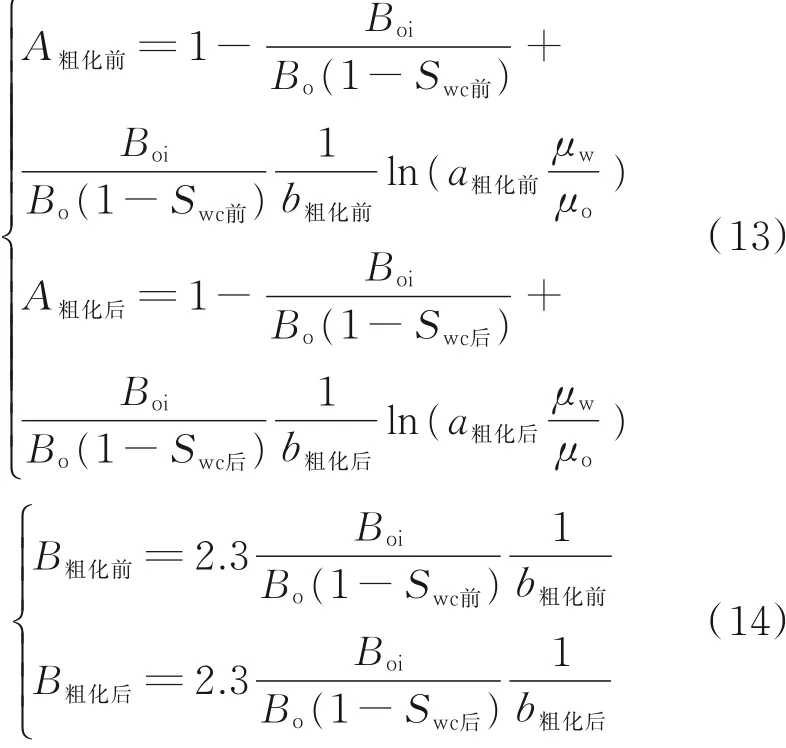
对式（13）联立作差得到：

假设各端点含水饱和度的值不变，即Swc前=Swc后，代入式（15）、（16）得到：

整理得：

式中，Swc前、Swc后分别为粗化前、粗化后束缚水饱和度，取值为0.17；a粗化前、a粗化后分别为粗化前、粗化后Kro/Krw与Sw的关系曲线直线段延长线在纵坐标轴上的截距；b粗化前、b粗化后分别为粗化前、粗化后Kro/Krw与Sw的关系曲线直线段的斜率；

将表1的数据代入式（19）、（20），得b粗化后=14.545 2，a粗化后=885.676 3，lna粗化后=6.786 4。从而可以得到粗化后的Kro/Krw与Sw的关系曲线直线段的表达式为：

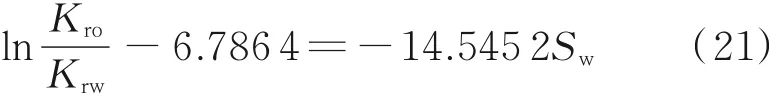
根据修改后的Kro/Krw和Sw，保持含水饱和度和油相相对渗透率不变，通过比值计算出水相相对渗透率，并运用数值模拟软件对开发效果进行预测，得到图5所示的结果。

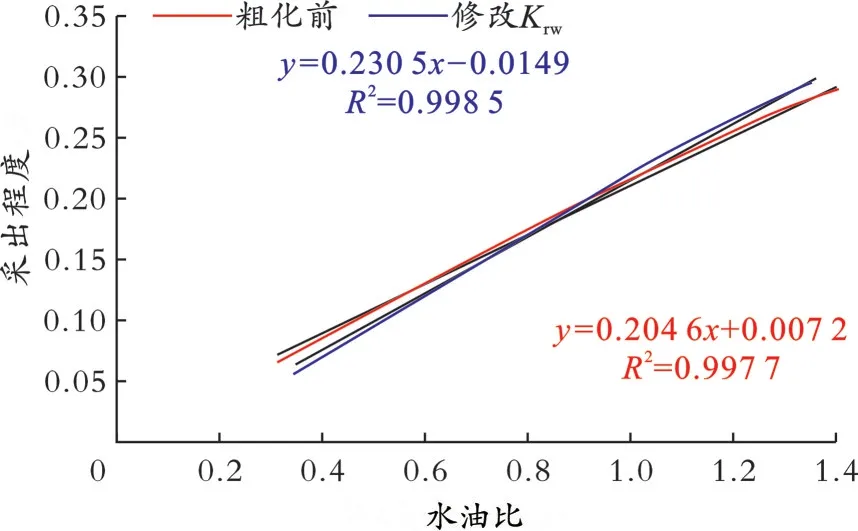
图5 16×16×3概念模型粗化前与修改Krw后水油比与采出程度关系Fig.5 The relationship curve between water⁃oil ratio and recovery degree before upscaling and after rewriting Krw of 16×16×3 conceptual model

采用修改后的相渗曲线计算出的效果并不能与粗化前完全重合，但是修改Krw后的水油比与采出程度关系曲线在位置上发生改变，证明通过计算相对渗透率曲线和水油比与采出程度关系并不能使开发效果实现完全的一致，因此我们需要对方法进行改进，以减少相互转化的误差和其他因素的影响，从而实现效果的一致。

6.种后管理。伊乐藻生长需要光照，但不能冒出水面，因此要根据水草长势逐步增加水位，始终确保水草顶部不冒出水面，可根据水草长势追肥或补种。

3.2 平移相对渗透率曲线法

在实际应用过程中，为了应用方便，可以将粗化后与粗化前的水油比与采出程度关系曲线近似看做两条平行的直线，由lg(Kro/Krw)与Sw关系函数可知，通过改变式（22）的截距可以改变油水两相的相对渗透率，从而起到改变开发效果的作用。因此，在油水两相相对渗透率比值保持不变的情况下，采用改变含水饱和度的大小来改变ln(Kro/Krw)与Sw关系函数的截距。

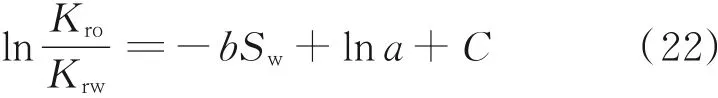
通过相渗曲线平移发现，含水饱和度值增加0.01时，水油比与采出程度关系曲线与粗化前基本重合，如图4所示，认为粗化后的开发效果可以与粗化前保持一致。

根据含水饱和度平移得到的规律，对含水饱和度平移距离与水油比和采出程度规律曲线截距进行曲线拟合，结果如图6所示，含水饱和度的增加值和水油比与采出程度拟合曲线的截距存在线性关系。

3.3 平移相渗曲线规律验证

根据某油田的渗透率数据，利用Eclipse数值模拟软件，建立概念模型。模型为三层，各小层的平均渗透率分别为2 549.89、4 736.15、1 828.57 mD，孔隙度为30%，厚度为10 m。模型中地层原油黏度为58.1 mPa⋅s，地层中水黏度为0.49 mPa⋅s，原始地层压力为14.28 MPa，含水饱和度为0.3，采用非平衡启动模拟，网格划分情况如表2所示。

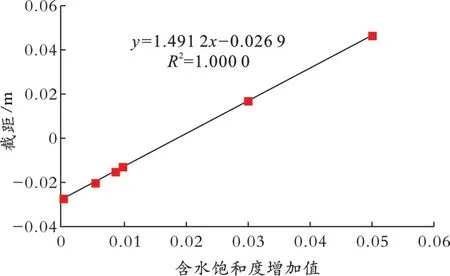
图6 16×16×3概念模型水油比与采出程度拟合截距随含水饱和度变化Fig.6 The change between water-oil ratio and recovery degree fitting intercept with water saturation of 16×16×3 conceptual model

表2 网格划分情况Table 2 Grid partitioning table

运用Eclipse数值模拟软件进行模拟计算，粗化前和粗化后油水井设置相同的工作制度，水井以80 m3/d定注入量注入，油井以80 m3/d定产液量生产，保持注采平衡，设置生产年限为30 a，得到粗化前和粗化后水油比与采出程度的变化曲线，结果如图7所示。由图7可知，粗化前与粗化后两条曲线存在明显差异，证明采用算数平均的方法对网格进行粗化并不能完全表征粗化前的渗透率属性。

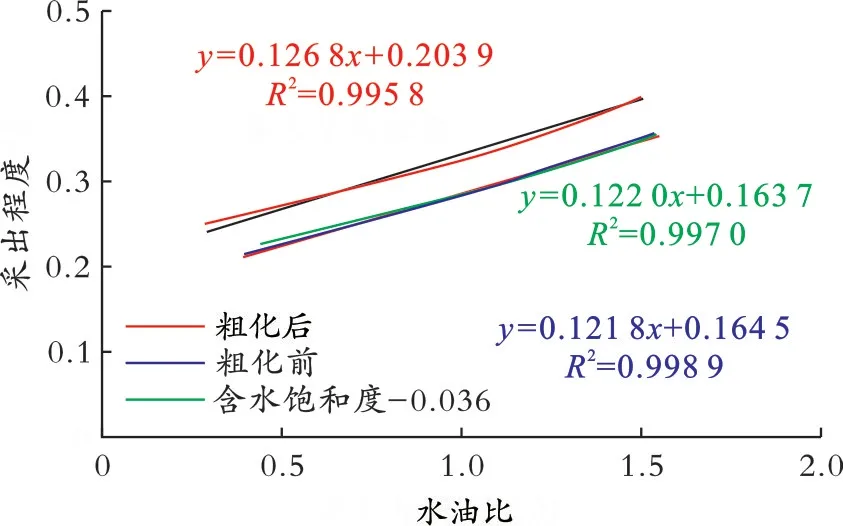
图7 27×27×3概念模型粗化前后和含水饱和度−0.036后水油比与采出程度关系Fig.7 The relationship between water⁃oil ratio and recovery degree before and after upscaling,after water saturation⁃0.036 of 27×27×3 conceptual model

通过整理粗化后相渗平移前后平移值和水油比与采出程度的截距，得到图8所示的关系曲线。该条直线可以计算出当粗化后与粗化前开发效果相同时需要含水饱和度的变化。计算得到当含水饱和度减小至0.036时，开发效果相同，证明了含水饱和度平移和水油比与采出程度的截距存在线性关系。

图8 27×27×3概念模型水油比与采出程度拟合截距随含水饱和度变化Fig.8 The change between water⁃oil ratio and recovery degree fitting intercept with water saturation of 27×27×3 conceptual model

3.4 分段平移相渗

在对水油比与采出程度关系曲线修正的过程当中，由于只考虑直线段的拟合，使最终的开发效果相同，但是忽略了油田开采早期水油比与采出程度曲线不满足直线段的部分，从而导致早期的开发效果并不能完全等效，结果如图9所示。根据直线段对相渗平移得到的规律，在此我们采用将开发效果分段拟合的方法，即分段平移相渗的方法，分别把每一段相渗曲线平移不同的距离，使前期也能达到相同的开发效果。

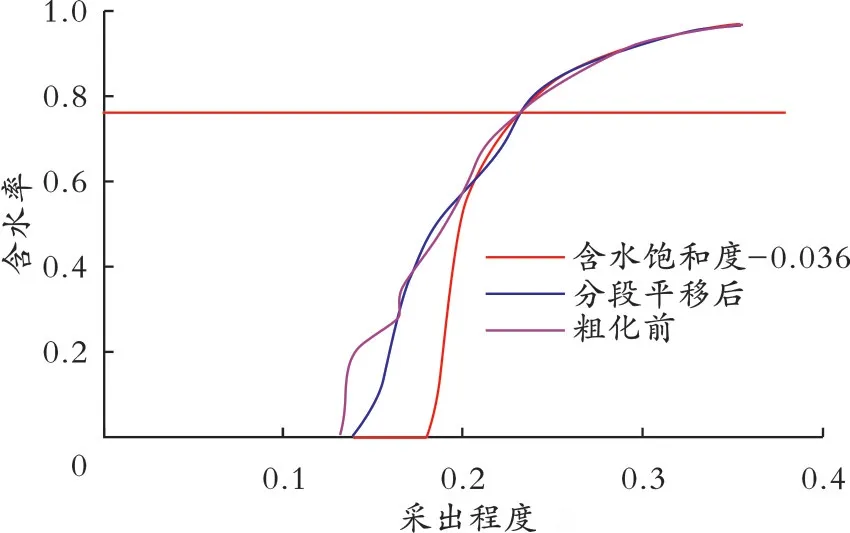
图9 27×27×3概念模型粗化前、含水饱和度−0.036后和分段平移后采出程度与含水率关系Fig.9 The relationship between recovery degree and water cut between before upscaling,after segmental translation and after water saturation-0.036

由图9可知，当含水率在74.8%以下时，粗化前与粗化并且修改含水饱和度后的采出程度与含水率关系曲线不能重合，证明在含水率为74.8%之前修改后的开发效果与粗化前不同，因此对相渗曲线中含水率为74.8%以前的点进行修改，含水饱和度减去0.05并把含水率为74.8%周围的点进行修改，使相渗曲线光滑，水油比与采出程度未成直线段的部分明显改变，粗化后采出程度与含水率的曲线明显在向粗化前靠近，得出通过分段平移相渗使非直线段的水油比与采出程度曲线与粗化前重合，从而达到开发效果的一致。

4 实例验证

4.1 井组模型建立

根据某油田实际地质模型，优选井组对调整相渗等效表征方法进行验证，其井组如图10所示，井组共有油水井12口，其中水井包括B6、B8、B13、B15、L21、L22、L23、L24，油 井 包 括B7、B14、L4、L7。

井组模型粗化前采用网格步长为30 m×30 m，网格数为36×33×120，粗化后采用网格步长为60 m×60 m，网格数为18×17×120，井组模型中的地层原油黏度为58.1 mPa⋅s，地层中水黏度为0.49 mPa⋅s，原始地层压力为14.28 MPa，采用非平衡启动模拟。渗透率属性采用调和平均的方法进行粗化，而孔隙度、净毛比和含水饱和度采用算数平均方法进行粗化，分别得到粗化前与粗化后的模型，结果如图11所示。

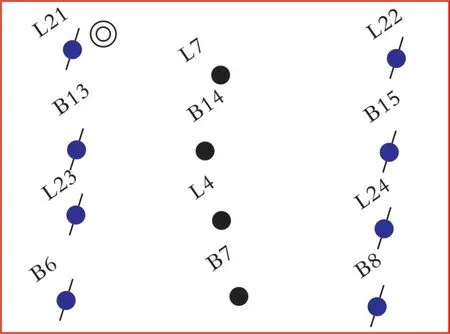
图10 实际井组井位示意Fig.10 Well location of actual well group

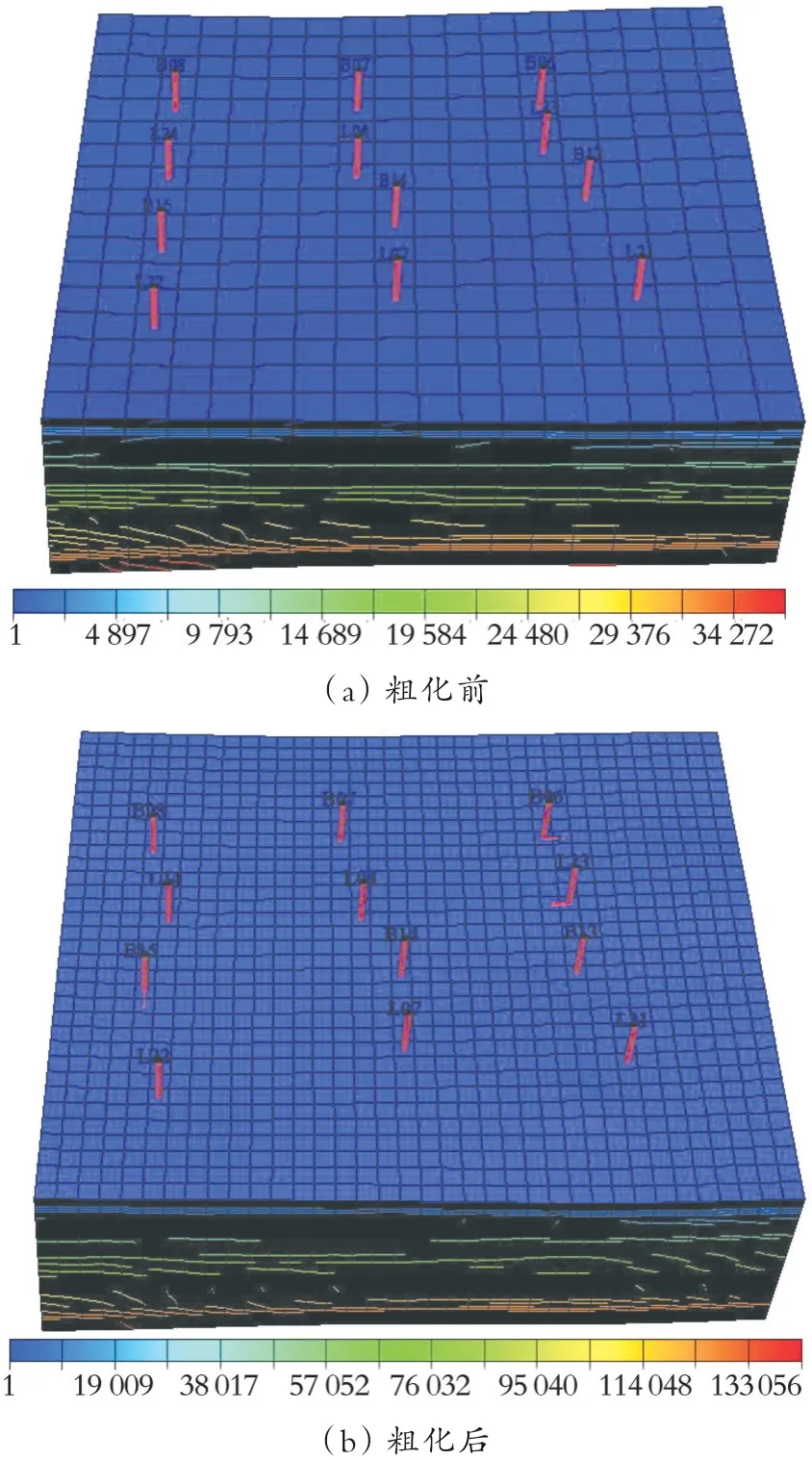
图11 粗化前与粗化后实际井组模型示意Fig.11 Schematic diagram of actual well group model before and after upscaling

4.2 井组模型平移规律验证

运用Eclipse数值模拟软件进行模拟计算，粗化前和粗化后油水井设置相同的工作制度，水井以300 m3/d定注入量注入，油井以600 m3/d定产液量生产，保持注采平衡，设置生产年限为30 a，计算得到水油比与采出程度的关系曲线，结果如图12所示。对粗化前与粗化后的水油比与采出程度的关系曲线取直线段处理，并对直线段进行拟合，得到其基本上为平行关系，可以采用平移相渗的方法对其水油比与采出程度曲线进行平移，最终达到开发效果的一致性。

图12 实际井组粗化前、粗化后和含水饱和度−0.03后水油比与采出程度关系Fig.12 The relationship between water⁃oil ratio and recovery degree before and after upscaling,after water saturation－0.03

通过整理粗化后相渗平移前和平移后的平移值和水油比与采出程度的截距得图13所示的关系曲线，该条直线可以计算出当粗化后与粗化前开发效果相同时需要含水饱和度平移的距离大小。由于粗化前水油比与采出程度关系曲线的截距为0.025 8，通过计算得到当含水饱和度减小0.03时，效果基本相同。计算相渗平移相渗后与粗化前的水油比与采出程度关系曲线之间的误差为3.16%，误差较小。

5 结论

（1）采用调和平均和算数平均两种方法对模型的渗透率进行粗化，其粗化后的采出程度与含水率的关系曲线与粗化前存在一定的差别，因此无论是调和平均还是算术平均都很难完全的等效表征粗化前的地质特征。

（2）基于油藏工程方法推导得到，Kro/Krw与Sw的关系曲线的斜率与截距和水油比与采出程度关系曲线的斜率与截距存在一定的函数关系，因此可以通过修改相渗曲线最终达到开发效果的一致。

（3）通过研究发现相渗曲线的平移距离和水油比与采出程度关系曲线的拟合直线的截距大小存在线性关系，因此可以根据粗化前水油比与采出程度关系曲线的截距，计算得到相渗曲线的平移距离，从而最终达到粗化后与粗化前开发效果曲线的相同。

（4）采用实际油田数据对相渗平移规律进行验证，采用平移后的相渗对粗化后的模型进行数值模拟，最终得到平移后与粗化前的水油比与采出程度关系曲线之间的误差为3.16%，精度较高。

图13 实际井组水油比与采出程度拟合截距随含水饱和度变化Fig.13 The change between water⁃oil ratio and recovery degree fitting intercept with water saturation of actual well group