基于自适应射频指纹地图的WSN室内定位算法研究*

刘晓叶，徐玉斌

（1.太原科技大学电子信息工程学院，太原030024；2.太原科技大学计算机科学与技术学院，太原030024）

基于自适应射频指纹地图的WSN室内定位算法研究*

刘晓叶1，徐玉斌2*

（1.太原科技大学电子信息工程学院，太原030024；2.太原科技大学计算机科学与技术学院，太原030024）

针对目前基于无线传感器网络进行室内定位时由于节点间收发信号的强时变特性而造成的定位精度不高、自适应性差的问题，提出了一种基于自适应射频指纹地图的WSN室内定位算法。该算法利用固定位置处信标节点间的信号强度来实时刻画环境的动态变化，从而构建出自适应环境变化的射频指纹地图；实时定位阶段，利用贝叶斯估计法计算目标初始位置，通过有限状态自动机滤除目标移动过程中出现的不可能跳变位置。实验结果表明，该方法在增加环境自适应性的同时大大提高了定位精度。

无线传感器网络；射频指纹地图；室内定位；有限状态自动机

随着对室内位置服务要求的不断增加，找到一种适用于室内环境的高精度、低复杂度及强环境自适应性的定位算法成了近年研究的热点。对于室内复杂环境来说，适用于室外定位的GPS系统和蜂窝移动网络在室内中的定位精度明显恶化，无法满足室内用户精确定位的需求。无线传感器网络以其具有灵活的网络拓扑结构、成本低、易于布署且能够自主组网等优点在室内定位中得到了广泛应用。

基于接收信号强度（RSSI）［1-2］的室内定位机制不用额外附加硬件，以其低成本、低能耗的优点受到了国内外研究者的青睐。基于RSSI的定位机制又可分为基于信号传播模型［3-4］及基于射频指纹地图［5］两种，由于室内环境复杂多变，信号传播模型并不能很好地表征目标接收信号强度与矩离间的关系，故本文采取基于射频地图的模式匹配法避免了信号传播模型的不确定性所造成的定位误差。

由于节点接收的信号强度具有较强的时变特性，采用静态射频指纹地图与实时测量的目标接收信号强度进行模式匹配的方法已不能满足某些场合的定位精度需求。为此，文献［6-7］中提出在定位区域中增加参考节点，通过挖掘参考节点信号与目标信号间的关联性，利用神经网络来动态构建射频地图，其成本与复杂度较高；文献［8-9］中采用补偿法对目标接收信号强度加上一个修正量后与原来的静态地图进行匹配，但定位精度不高；文献［10］提出利用众包更新指纹库的方法，但需定期对过期指纹进行筛减。

对于移动目标来说，传统的定位算法都是将目标的移动过程看作是一系列的目标定位过程，由于目标处于不断的移动过程当中，在某一位置处接收到的信号强度受噪声影响很大，采用与射频指纹地图全局匹配的定位算法不但计算复杂度高，还容易形成大的跳变，造成定位精度下降。

本文利用无线传感器网络中的信标节点来实时监测环境的时变特性，从而构建出自适应环境变化的射频地图，在不增加额外附加节点开销的同时提高了定位精度。对于移动目标来说将有限状态自动机计算模型引入到移动目标的定位过程中，滤除了目标的不可能跳变位置，大大提高了定位精度。

1 自适应射频指纹地图的构建

基于射频指纹地图的定位过程主要分为射频地图的离线构建与目标实时定位两个阶段。为达到高精度定位，构建出能自适应环境变化的射频指纹地图至关重要。由于无线传感器节点的无线通信模块具有收发信号的功能，所以本文中采用的方法如图1所示无需附加额外参考节点，直接运用提前布置在固定位置处的信标节点间的信号强度来实时监测环境的变化并将此变化动态地反映到射频指纹地图中，从而构建出自适应环境变化的射频指纹地图。其中Bij表示信标节点j接收到的来自信标节点i的信号强度，Sig表示目标在位置g处接收到的来自信标节点i的信号强度。

图1 信号强度分布图

1.1 静态射频指纹地图的改进

传统的静态射频指纹地图的形式为S=（x，y，Sig），离线时将待定位区域划分成网格状，每一网格中心处为一参考点，用二维坐标（x，y）表示射频地图中参考点的位置坐标，Sig表示目标在参考点位置g处接收到的来自信标节点i的信号强度均值，此地图的缺点是没有固定的反映当前地图环境特性的量。为此，找到一个能刻画环境变化的量至关重要，由于无线通信模块具有收发信号的功能，而基于射频地图的定位方法中信标节点位置是固定的，所以本文利用信标节点间的信号强度Bij来刻画当前环境特性，射频地图形式可表示为S=（x，y，Sig，Bij，Wijg），Wijg表示目标位置处接收到来自信标节点i的信号强度Sig与信标节点j（j≠i）接收到信标节点i的信号强度Bij间的关联性矩阵。

文献［7］［9］中提出不同位置点处接收到的来自同一信标节点的信号强度具有空间关联性，其模型可用线性方程近似表示为

本文实验在平均每12米的覆盖区内布置四个信标节点，分别记为B1、B2、B3、B4，以信标B1发射信号为例，各参考点处接收到的来自该信标节点的信号强度S1g=［S11S12… S1g］，其它信标节点接收到来自B1的信号强度B1j=［B12B13B14］；其中S1j与B1g分别取单位时间内接收信号强度的几何平均值，它们之间的空间关联性可表示为：

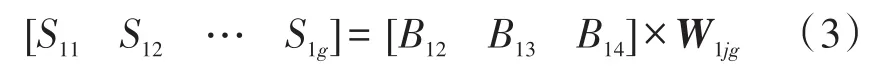
其中

同理可以求得各信标节点间信号强度Bij与各参考点处接收信号强度Sig间的关系矩阵Wijg。

1.2 射频指纹地图的实时更新阶段

实时定位时观测到的目标接收信号强度可表示为o=（o1，o2，o3…oi），其中oi表示目标接收的由信标节点i发射的K个数据样本，oi=［oi1，oi2…oik］T；信标节点间的信号强度为Bij′=（B1j′，B2j′，B3j′），其中Bij′表示实时观测到的信标节点j接收到的由信标节点i（i≠j）发射来的信号强度均值。利用1.1节求出的关系矩阵根据式Sig′=Bij′×Wijg，可以得到自适应环境变化的射频指纹地图S′=（x，y，S1g，S2g，S3g，S4g）。

2 实时定位阶段

定位问题即为找到一个函数映射ƒ，通过定位观测值o与射频指纹地图信息进行模式匹配最终得到目标节点位置z。基于射频指纹地图的模式匹配算法大致可分为两种：确定型定位算法［11］与概率型［12-13］定位算法。概率型定位算法充分考虑到了位置的先验信息及复杂环境因素干扰导致的不确定性，具有较好的抗干扰性能和较高的定位准确度，其性能优于确定型定位算法。

本文采用基于最大后验概率的贝叶斯估计法与自适应射频指纹地图进行匹配得到目标初始位置，然后通过有限状态自动机模型来滤除不可能的跳变位置。

2.1 贝叶斯估计法

定位时，设目标节点观测到接收信号强度为o=（o1，o2，o3…），目标节点位置为z，其目标定位问题可看做是基于最大后验概率的贝叶斯估计问题

式中：p（zi）为先验概率函数，分母是一个归一化权值，后验概率值实际上只与p（o|zi）有关。

长时间内目标接收到的来自同一信标节点的信号强度频率直方图如图2所示近似为高斯分布。所以p（ok|zi）可用高斯核函数的和来表征：

式中：ni表示在线阶段目标位置处收集到的观测样本数目，okj表示在线阶段目标位置处接收到的来自信标节点K的第j个观测值，Sk表示射频地图中对应位置处的目标接收信号强度，h为高斯窗的宽度。

图2 目标接收信号强度分布图

由于目标接收到各个信标节点的信号强度是互不影响的，所以目标接收信号强度的概率密度函数p（o|zi）为各个信标处的概率密度函数的乘积：

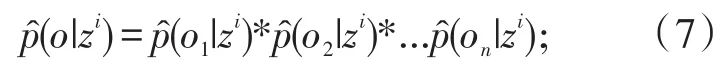
具体的贝叶斯估计算法流程如表1所示。

表1 贝叶斯估计算法流程

2.2 移动节点运行状态的有限状态自动机模型

有限状态自动机是一具有离散输入输出系统的数学模型，它能够实现状态转移，对于一个给定的属于该自动机的状态和一个属于该自动机字母表的字符，它都能根据事先给定的转移函数转移到下一个状态。用五元组可表示为：A=（Q，∑，δ，q0，F）。Q为状态的非空集合，∀q∈Q,q为A所处的状态；∑为输入字母表或是状态转移条件，∑={a，b，c…}；δ为状态转换函数，δ：Q×∑=Q，例：δ（q，a）=p，（p，q∈Q）；q0为非空的开始状态，q0∈Q；F为终止状态或是一个接受状态的集合，F∈Q。

上式中所定义的有限状态自动机的转移状态是确定的，称为确定性有限状态自动机，它从起始状态开始，一个字符一个字符地读入字符串｛a，b，…｝，并根据给定的转移函数一步一步地转移至下一个状态。在读完字符串后，如果该自动机停在一个属于F的接受状态，那么它就接受该字符串，反之则拒绝该字符串。

基于有限状态自动机原理，可将移动节点的状态划分成四类：Q={开始状态q0、正常预测状态q1、异常状态q2、错误状态q3}；定义∑=｛a，b｝为移动节点状态转移条件；其具体情况为

①状态转移条件a：移动节点的运动过程符合马尔科夫模型，即当前时刻位置在前一时刻位置为中心最大移动距离为步长的位置集合中；实验统计得出目标接收信号强度与位置集合匹配的概率阈值P*及前后几次定位误差阈值d*；将实际定位时满足匹配概率P＞P*且定位误差d＜d*为真的条件定为a。

②状态转移条件b：将P＞P*且d＜d*为假的条件定为b。

③开始状态q0：据2.1节贝叶斯估计法匹配得到的目标位置。

④正常预测状态q1：满足条件a（错误态除外）的目标状态。

⑤异常预测状态q2：目标预测时出现异常态的原因大致有两种。一种是上次定位有误差，以上次位置为中心进行搜索匹配时会出现误差的积累；另一种是由于环境变化导致接收信号产生奇异值。此时不能满足条件a，出现异常。

⑥错误状态q3：目标产生异常状态时可采用扩大搜索区即取2倍的最大移动步长为搜索区域的方法继续匹配，如满足条件a会转移到正常状态q1，如仍不能满足a则产生错误态，产生此态时应滤除。

移动节点运行状态的有限状态自动机模型如图3所示。

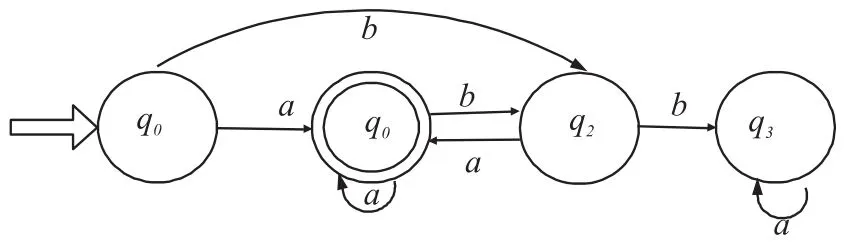
图3 移动节点运动状态的自动机模型

状态转移表如表1所示。

表2 状态转移表

对应的转移函数为：δ（q0，a）=q1；δ（q0，b）=q2；δ（q1，a）=q1；δ（q1，b）=q2；δ（q2，a）=q1；δ（q2，b）=q3；δ（q3，a）=q3；δ（q3，b）=q2。

通过有限状态自动机模型，逐渐滤除了目标的跳变位置（错误态q3），接受了目标的正常预测态q1，提高了移动目标的预测精度。

3 实验结果与分析

3.1 实验平台与环境

本文硬件部分采用的是Crossbow公司的MIB520接口板和IRIS传感器节点。IRIS节点平台是基于ATmegal1281微处理芯片和RF230射频芯片且工作在2.4 GHz、支持IEEE 802.15.4协议的Mote模块，它支持的最大数据传输率为250 kbit/s，在户外视距内无信号放大器的情况下信号可传播500 m，可用于低功耗的无线传感器网络；用MIB520接口板作为无线传感器网络与PC机的通信网关。

本实验是在包括1个房间和1个走廊的面积为20 m×15 m（如图4所示）的区域内进行。构建射频地图之前将待定位区域划分为1m×1m的网格状，图中黑色圆点为地图训练阶段的参考点位置，用二维坐标（x，y）来表示，信标节点布置在矩形区域的4个顶点上，以保证每个参考点处都有4个信标节点覆盖。

图4 实验环境布局图

3.2 节点接收信号强度的时变特性实验与分析

由于室内环境复杂多变，节点接收到的信号强度受反射、散射及噪声等干扰具有较强的时变特性。图5、图6分别表示不同时间段在位置Z1、Z2处观测到的来自不同信标节点的信号强度直方图。

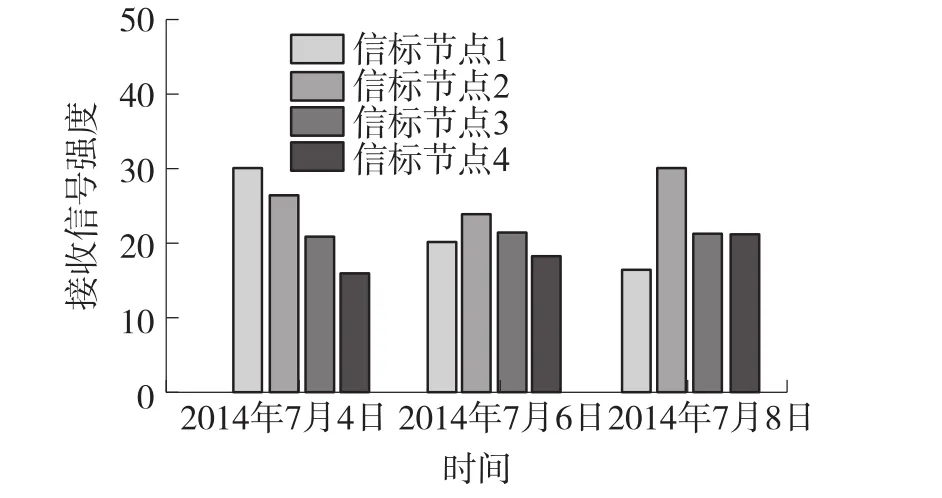
图5 位置Z1处目标接收信号强度直方图

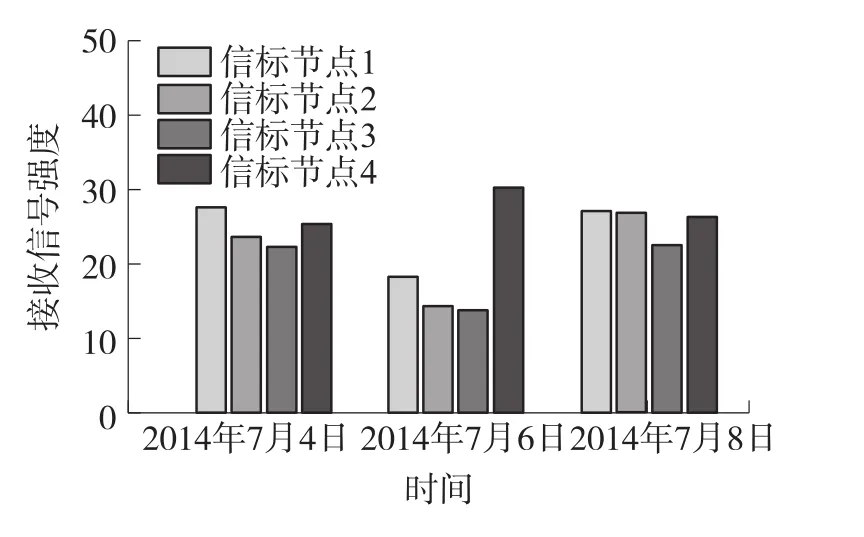
图6 位置Z2处目标接收信号强度直方图

实验表明节点间的信号强度存在较强的时变特性，定位匹配时仍采用静态射频地图的方法已不能满足高精度定位的需求。

3.3 定位效果比较与分析

本文利用贝叶斯估计法与自适应射频指纹地图进行匹配来得到目标初始位置，定位结果如图7所示。与静态地图匹配方法和直接补偿方法相比，本文采用自适应射频指纹地图匹配方法的定位精度能以80%的概率达到2 m，100%的概率达到3 m，以1 m的平均定位误差优于传统算法。

图7 不同方法的位置误差比较

3.4 不同信标节点数对定位误差的影响

对于一常见的室内矩形区域来说，不同信标节点数对定位误差有很大影响。如图8所示，结果表明信标节点在2个及以下时定位误差较大，信标节点数为4个时定位精度较高，能以80%的概率达到2 m的误差，而信标节点数为5个时，定位精度并没有很大的提高，所以对常见的室内矩形区域覆盖来说，采用4个信标节点即可达到室内定位需求。

图8 不同信标个数误差比较

3.5 采用有限状态自动机对定位精度的影响

本文采用贝叶斯估计法计算出目标的初始位置，然后采用马尔科夫模型对目标进行局部搜索，同时结合有限状态自动机模型滤除目标的不可能跳变位置。

移动目标跟踪图如图9所示，其中x、y表示平面区域的二维坐标，移动目标沿着坐标位置（1.5，1.5）到（16.5，16.5）并由（16.5，16.5）到（29.5，1.5）的对角线方向移动。用（Xi，Yi）坐标标示的点为几个典型的用贝叶斯法估计位置，距离目标实际位置误差较大，文中将这些位置点称作跳变位置；用（Xi′，Yi′）坐标标示点为本文方法所估计出的对应（Xi，Yi）的目标位置。实验结果显示本文给出的方法与单用基于最大后验概率的贝叶斯估计法相比显著提高了目标的定位精度。

图9 位置跟踪图

4 结束语

由于室内环境复杂多变，无线传感器节点间的信号强度具有较强的时变特性，采用传统静态地图匹配的定位方法误差较大。本文利用信标节点来监测环境的实时变化，并根据信号强度的空间关联性模型，在离线阶段得到信标节点间与各参考点处来自各信标节点间的关联性矩阵，用实时监测到的信标节点间的信号强度来动态更新射频指纹地图，该方法具有较强的环境自适应能力。此外将有限状态自动机模型运用到移动目标定位过程中，滤除了不可能的跳变位置，进一步提高了定位精度。

［1］Bahl P，Padmanabhan V N.RADAR：An in-Building RF-Based User Location and Tracking System［C］//IEEE Infocom，2000（2）：775-784.

［2］苟胜难.基于改进的RSSI无线传感器网络节点定位算法研究［J］，计算机应用仿真，2012，29（5）：1867-1869.

［3］方震，赵湛，郭鹏，等.基于RSSI测距分析［J］.传感技术学报，2007，20（11）：2526-2530.

［4］赵昭，陈小惠.无线传感器网络中基于RSSI的改进定位算法［J］.传感技术学报，2009，22（3）：391-394.

［5］赵方，罗海勇，马严，等.基于公共信标集的高精度射频指纹定位算法［J］.计算机研究与发展，2012，49（2）：243-252.

［6］Yin J，Yang Q，Ni L.Learning Adaptive Temporal Radio Maps for Signal Strength Based Location Estimation［J］.IEEE Trans on Mobile Computing，2008，7（7）：869-883.

［7］林以明，罗海勇，李锦涛，等.基于动态Radio Map的粒子滤波室内无线定位算法［J］.计算机研究与发展，2011，48（1），139-146.

［8］郭红成，罗海勇，尹浩，等.基于线性插值和动态指纹补偿的分布式定位算法［J］.传感技术学报，2009，22（12）：1795-1801.

［9］李方，王铁成，佟为明.基于空间变异理论的电子地图构建方法［J］.哈尔滨工程大学学报，2012，33（6）：715-719.

［10］李燕君，徐凯锋，邵剑集.利用众包更新Wi-Fi室内定位指纹库的方法研究［J］.传感技术学报，2014，27（12）：1692-1698.

［11］Lo C C，Hsu L Y，Tseng Y C.Adaptive Radio Maps for Pattern-Matching Localization via Inter-Beacon Co-Calibration［J］.Perva-sive and Mobile Computing，2012，8（2）：282-29.

［12］宋越明，于宏毅.采用概率密度分布和粒子滤波的室内跟踪算法［J］.计算机工程与应用，2010，46（1）：237-240.

［13］崔丽珍，李蕾，员曼曼，等.基于核函数法及粒子滤波的煤矿井下定位算法研究［J］.传感器技术学报，2013，26（12）：1728-1733.

刘晓叶（1989-），女，硕士生，主要研究方向为无线传感器网络，yeziliu89@sina.com；

徐玉斌（1964-），男，教授，主要研究方向为无线传感器网络、物联网、工业控制网络等，xyub@163.com。

Indoor Localization Algorithm Research Based on Adaptive Radio Fingerprinting Map and WSN*

LIU Xiaoye1，XU Yubin2*
（1.School of Electronics and Information Engineering，Taiyuan University of Science and Technology，Taiyuan 030024，China；2.College of Computer Science and Technology，Taiyuan University of Science and Technology，Taiyuan 030024，China）

In order to improve the positioning accuracy and environmental adaptability which is caused by the fluctuation of the received signal strength for the WSN-based indoor positioning systems，this paper presents a new indoor location algorithm which is based on adaptive radio fingerprinting map and WSN.It utilizes signal strength between beacon nodes at the fixed location to describe the environmental dynamic changes in real time and develops the adaptive radio fingerprinting map.In real-time positioning stage，it uses the Bayesian estimation method to get target initial position，and then filter the impossible mobile target position by utilizing the finite state automation.Extensive experiments show that the proposed algorithm not only increases the environmental adaptability，but also greatly improves the positioning accuracy.

WSN；radio fingerprinting map；indoor location；finite state automata

TP393

A

1004-1699（2015）08-1215-06

��7230；6210

10.3969/j.issn.1004-1699.2015.08.019

项目来源：晋城市科技计划项目（201501004-1）

2014-11-10 修改日期：2015-05-13