电热驱动Bimorph微执行器对流系数估算方法研究*

刘骏文，徐大诚，陈 巧，丁金玲，谢会开

（1.苏州大学电子信息学院，江苏苏州215000；2.无锡微奥科技有限公司，江苏无锡214000；3.美国佛罗里达大学电气与计算机工程系，美国佛罗里达州32611）

电热驱动Bimorph微执行器对流系数估算方法研究*

刘骏文1，2，徐大诚1*，陈 巧2，丁金玲2，谢会开3

（1.苏州大学电子信息学院，江苏苏州215000；2.无锡微奥科技有限公司，江苏无锡214000；3.美国佛罗里达大学电气与计算机工程系，美国佛罗里达州32611）

随着电热驱动MEMS器件尺寸进一步缩小，传统热对流系数的取值已无法满足微系统分析建模需求。针对电热型Bimorph结构的MEMS微镜驱动器，通过分析其温度分布，并以其平均温度为参考指标建立简单热阻和对流热阻分段模型，推算出微尺度下精确的对流系数，提高了微执行器设计模型的驱动性能。经理论计算和实验测试验证，对流系数值的误差在8.1%以内，满足实际设计需求，验证了该方法的合理性和可行性。

对流系数；电热Bimorph结构；微执行器；热阻模型

近年来，微机电系统（MEMS）获得了高速发展，电热驱动MEMS器件应用越来越广泛［1-3］。对微小尺寸下热传递的探讨与研究也就显得越来越重要，成为当前研究的热点［4］。在宏观尺度下，对流系数典型值为2 W/（m2·℃）～25 W/（m2·℃）［5］；当尺度在100μm以下，Peirs建议对流系数可取100 W/（m2·℃）［5］。但是随着尺寸进一步减小，研究发现，已有的对流系数参考值已无法满足实际要求。在MEMS微镜模型创建和性能分析时，采用电热驱动Bimorph执行器的几何尺度为14 μm×700 μm，若用上述对流系数参考值来计算Bimorph温度时，发现与实际测得温度有很大差距，给执行器驱动能力的设计带来较大困难。

目前，微小尺寸下的自然对流系数测量和计算的方法已有一些研究，如：（1）考虑边界条件的理论研究计算方法［4］；（2）瑞利数、格拉晓夫数、普朗特数、努赛尔数的经验公式，如经典的Morgan［6］、Churchill［7］和Yang［8］关系式；（3）微细金属丝的实验测试方法［9-10］，等等。但基于边界条件的方法过于复杂，经验公式法和经典公式有诸如尺寸及形状等条件的限制，实验测试法又受限于实验对象和条件的影响，很多时候都不太实用。这样就很有必要找到一种简单可行方法，计算出热驱动环境的实际对流系数。

本文针对电热型MEMS微镜的执行器Bimorph结构，在建立简单热阻和对流热阻分段模型的基础上，推算出微尺度下的对流系数。该方法求得的对流系数能够满足MEMS微镜热驱动系统的设计要求。

1 电热Bimorph结构及原理

图1为电热驱动MEMS微镜执行器［11］结构。如图1（a）中所示，此微执行器由两个相同的双S型结构轴对称连接而成，而每个“S”都是由两个相同的Bimorph结构反向串联而成。通过对称设计使执行器末端消除了侧向位移，实现了单一垂直位移功能。

如图1（c）所示，Bimorph是由Al和SiO2两种不同材料组成的两层结构［12］。由于Al和SiO2的热膨胀系数不同，故在相同温度下，两者膨胀大小不同，致使Bimorph结构发生弯曲；当Bimorph一端固定时，另一端就实现了偏转运动，从而达到致动的效果，其运动过程如图1（c）所示。在Al和SiO2两层之间嵌入一层薄而窄的金属Ti作为Bimorph的加热器；当给Ti两端通电时，Ti开始发热，并将热量提供给Al和SiO2。

图1 Bimorph及微镜执行器结构图

2 Bimorph热传导分析

2.1 建立Bimorph热阻模型

为了分析Bimorph的热传导过程，需建立简单模型，并以此模型分析Bimorph的温度分布和空气对流系数。

如图1所示，为使加热器产生的热量尽可能作用于Bimorph上，需要抑制Bimorph上的热量流向衬底，故在Bimorph与衬底之间连接了一段SiO2热隔离块。Bimorph本身热阻用R0表示，相应的SiO2热隔离块热阻用R1表示，空气对流热阻用RBC表示，且RBC=1/（h·s）其中h为对流系数，S为Bimorph的对流面积。由于Bimorph整个长度上都与Ti并联，故Bimorph顺着延伸方向的每个点都是热源。为方便和简化，将Bimorph平均分为n段，且每一段都作为一个热源。

Bimorph分为n段后，其本身热阻表现为串联，对流热阻表现为并联，故两者分段后每段的热阻值分别为其原热阻值的1/n和n倍，即nRBC和R0/n。同时，根据热传递原理，Bimorph上的温度差ΔT、功率P和热阻Rr存在关系［13］：ΔT=P*Rr。由此，建立满足上述要求的热阻模型，如图2所示。其中：Ti（i=1+…n+1）为第i段左端的温度，Pi（i=1+…n+1）为Bimorph各段的输入功率。

图2 n段热阻模型

2.2 模型分析

图2热阻模型中，空气对流系数直接影响对流热阻RBC，导致热传递发生变化，最终影响到Bimorph的温度分布和功率分布。

对于Bimorph，初始时Ti和Bimorph结构每一处的温度是相同的，故每一段的电阻也相同，都为总电阻的1/n。当加入电压后，因热传递影响，Bimorph在其延长方向上产生了温度梯度。

考虑到Ti是温度敏感材料，其电阻在一定范围内随温度变化成线性关系，即Re（T）=Reo*（1+α*ΔT），其中Re0为初始电阻，α为电阻温度系数，ΔT为温度变化。故当Bimorph在延长方向上有温度梯度时，加热器Ti在延长方向上也会产生电阻梯度，即Bimorph温度分布影响Ti电阻分布。由于Bimorph上仅有一条电通路，故其每一段通过的电流都一样；而功率P=I2*R，故Bimorph上各段功率随电阻的不同而不同，即电阻的分布影响功率的分布。

由上述可知，Bimorph温度分布影响功率分布。而功率作为热的根本来源，其分布也必然会影响热传递，从而造成温度的分布。此时就形成了温度与功率互相关联的状态，给两者的求解带来了困难。

2.2.1 Bimorph温度分布的推导

由于温度分布与功率分布相互关联，故分三步来解这个问题：①假定温度分布已知，求此时的功率分布；②假定功率分布已知，求此时的温度分布；③综合上两步获得的关系式，求解温度与功率分布。

①假定温度分布已知，求此时的功率分布。

设初始温度为0℃。故加热器Ti电阻平均分成n段后，第i段电阻随温度的关系为：

简记，表示第i段的温度。

由此可知第i段的功率：

同时，又有总功率：

由式（2）（3）消去变量电流I可得：

令 Jn=[1,…,1]T，其中有 n个元素 1；令 t= [t1,…，tn]T，P=[p1,…，pn]T，则式（4）可拓展为：

式（5）就是已知温度分布求功率分布的公式。

②假定功率分布已知，求此时的温度分布。

根据图2的n段热阻模型，若Pi（i=1…n）已知，则Bimorph的各段的温度为：

式中，ai,j.是模型中功率 pj对温度ti的等效热阻，并由热阻模型本身决定。对其拓展可得：

因热阻模型中存在T和P，故为求矩阵A，可先求t与T的关系、T与P的关系。

ti代表Bimorph第i段的平均温度；图2中，Ti和Ti+1为第i段左右两端的温度，则ti=(Ti+Ti+1)/2。令T=[T1…Tn]，则有：

由图2模型，对温度TI有：

式中的系数ci,j是模型中功率 pj对温度Ti的等效热阻，由热阻模型本身决定。对式（9）拓展可得：

由式（7）～式（10）可得：

其中矩阵B已经获得，则对矩阵A的求解归结为矩阵C的求解。

由图2模型可知，当将某个功率分布代入模型后，就可以得到对应的温度分布。由此可知，n个不同的功率分布列向量PK（k=1…n），对应着n个不同的温度分布列向量，且有关系TK=CPK,(K=1…n)。则有：

由式（12）可得：

为简化计算，令P1…Pn分别取n阶单位矩阵的n个列向量，即Pjk=1,j=k;Pjk=0，j≠k;。将上述产生的n个功率分布向量分别代入到软件Multisim或Simulink中建立的热阻模型中（如图2所示），获得对应的n个代表温度分布的列向量，即，则由式（14）即可得到矩阵C：

式中：Pe=1，单位为mW。

由式（11）可求得矩阵A，则此时就得到由功率分布求温度分布的关系式（7）。

③综合式（5）和式（7），利用MATLAB软件就可以解出所需的温度分布和功率分布。

3 空气自然对流系数的推导

热量传递有3种方式：热传导、热对流和热辐射［13］。因材料热传导系数几乎不变，故热传导的热阻值都可认为是定值。计算得到，温度低于500 K时，Bimorph热辐射消耗功率不到总功率的0.7%，故可忽略其影响。故通过建立Bimorph结构的热阻模型，可以分析其热对流，进而得到相应的自然对流系数。

热对流系数在微小尺寸下，是一个不确定量，即对流热阻RBC的不确定，如此就导致模型热传递随之发生变化，最终使温度与功率分布发生变化。则根据Bimorph平均温度与对流系数的关联性，利用所建的热阻模型，就可以找到满足特定平均温度的对流系数值。

为了寻找满足要求的对流系数值，需通过搜索法来查找最优解。考虑到查找的准确性和速度，具体选取黄金分割法来搜索最优的对流系数h。首先设定初始对流系数值，代入到模型中；利用上节的知识推导出Bimorph的温度分布，再对其积分并取平均作为Bimorph的平均温度；若Bimorph平均温度与实际测试的平均温度TC相等或在误差范围内，则结束搜索，否则改变对流系数值，重复之前的步骤。具体过程如图3所示。

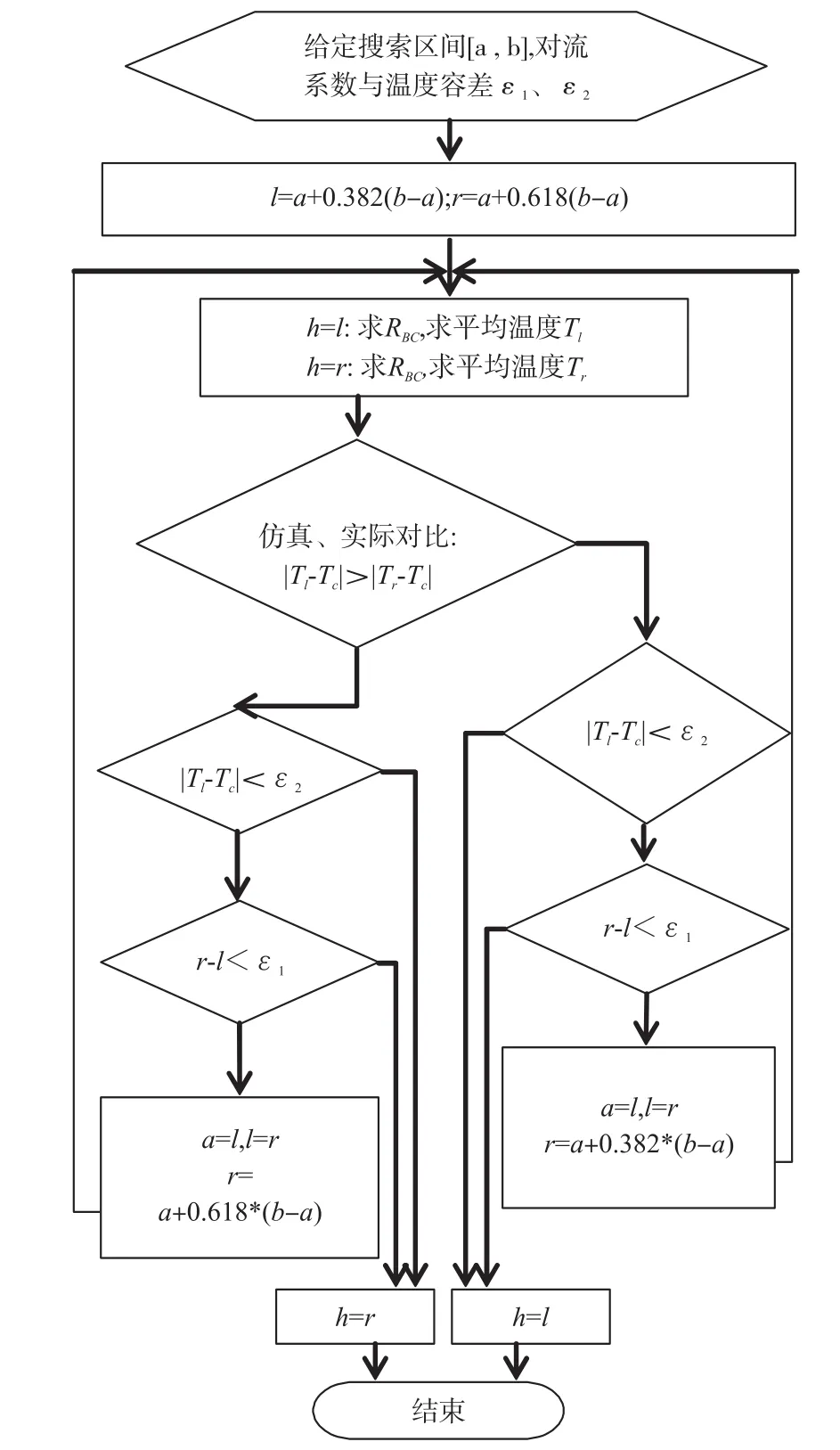
图3 对流系数推导流程图

4 模型仿真测试结果及对比分析

为验证模型及算法的可行性，本文分别对5、10、20、40、80、160段的模型进行仿真，其中平均温度精度取0.01℃。仿真中所需参数如表1所示，仿真结果如表2所示。

表1 仿真测试参数表

表2 对流系数仿真结果表

经典的Morgan经验关系式［6］：

式中：Nμd为努塞尔数，d为特征长度，λ为空气热导系数，Rad为瑞利数。

根据Morgan关系式计算得到的对流系数为hL= 1 058 W/（m2·℃）。对比可知，通过简单实验及模型关联推导的对流系数h与Morgan经验公式获得的值非常接近，误差为5.1%～8.1%，说明了该方法的合理性。当前模型中的参数除对流热阻是不确定的以外，其他参数都是确定的，故在温度不影响到这些确定参数时，该方法获得的流系数依然是正确的，在此温度范围内对流系数结果提取具有重复性。考虑到Bimorph的结构、材料等因素的不同会造成模型的变化，需在本文模型基础上，进行改善重新推导对流系数。

5 总结

提出了一种基于电热Bimorph微执行器空气自然对流系数的估计方法。建立Bimorph结构的简单热传递模型，分析Bimorph的温度和功率分布，进而获得其温度分布；以平均温度为参考指标，利用MATLAB及其Simulink工具，搜索到满足要求的自然对流系数。通过与经验公式比较，其误差在8.1%以内，是常用大尺度下自然对流系数的44倍以上［14］［15］。该对流系数的推算方法，验证了对流系数在微尺度下远大于宏观尺度，解决了微尺度下对流系数难以确定的问题，对电热型MEMS的散热及其温度分布等的研究具有一定的参考价值。

［1］SamuelsonSean R，Wu Lei，SunJingjing，et al.A 2.8-mm Imaging Probe Based on a High-Fill-Factor MEMS Mirror Andwire-Bonding-Free Packaging for Endoscopic Optical Coherence Tomography［J］.J Microelectromech Syst，2012，21（6）：1291-1302.

［2］Wu Lei，Dooley Sarah，Watson Edward A，et al.A Tip-Tilt-Piston Micromirror Array for Optical Phased Array Applications［J］.J Microelectromech Syst，2010，19（6）：1450-1461.

［3］陈建君，朱永，刘波，等.基于MEMS微镜的傅里叶变换光谱仪原理与分析［J］.光谱学与光谱分析，2012，32（11）：3151-3154.

［4］HuXJack，JainAnkur，GoodsonKennethE.InvestigationoftheNatural Convection Boundary Condition in Microfabricated Structures［J］.InternationalJournalofThermalSciences，2008（47）：820-824.

［5］Peirs Jan，ReynaertsDominiek，BrusselHendrikVan.Scale Effects and Thermal Considerations for Micro-actuators［C］//Proceeding of the 1998 IEEE International Conference on Robotics and Automation，1998（2）：1516-1521.

［6］Morgan V T.Advance in Heat Transfer［M］.New York：Academic Press Inc，1975：199-264.

［7］Churchill Stuart W，Chu Humbert H S.Correlating Equations for Laminar and Turbulent Free Convection from a Horizontal Cylinder［J］.Heat Mass Transfer，1975，18（9）：1049-1053.

［8］杨世铭.细长竖圆柱外及竖圆管内的自然对流换热［J］.西安交通大学学报，1980，14（3）：114-130.

［9］侯亚丽，王秀春，张承武，等.微细金属丝在空气中的自然对流换热的实验研究［J］.工程热物理学报，2007，28（3）：460-462.

［10］管宁，刘志刚，梁世强，等.微细金属丝在空气中自然对流换热［J］.北京工业大学学报，2009，35（7）：977-981.

［11］Chen Q，Zhang H，Zhang X，et al.Repeatability Study of 2D MEMS Mirrors Based on S-Shaped Al/SiO2Bimorphs［C］//Proc of 8th IEEE International Conference on Nano/Micro Engineered and Molecular Systems（NEMS）.Suzhou：IEEE，2013，817-820.

［12］Samuelson S R，Xie H.A Large Piston Displacement MEMS Mirror with Electrothermal Ladder Actuator Arrays for Ultra-Lowtilt Applications［J］.Micro-Electro-MechanicalSystems，2013，23（1）：39-49.

［13］章皓，徐大诚，陈巧，等.一种电热式MEMS微镜多自由度模型解析方法［J］.传感器与微系统，2014，33（10）：17-24.

［14］刘庆海，黄见秋.表面微机械MEMS温度传感器研究［J］.传感技术学报，2015，28（3）：325-329.

［15］刘莹，苑伟政，常洪龙.基于TPWL方法的MEMS热微执行器的热电耦合宏建模［J］.传感技术学报，2015，28（4）：455-461.

刘骏文（1990-），男，硕士研究生，研究方向为MEMS传感器建模与控制研究，liujunwen1990@foxmail.com；

徐大诚（1963-），男，教授，从事信息获取与智能处理技术和传感器信息融合与处理研究，xudacheng@suda.edu.cn；

陈 巧（1982-），男，博士，技术经理，从事MEMS传感器设计研究；

丁金玲（1982-），女，硕士研究生，MEMS工程师，从事MEMS传感器设计研究；

谢会开（1967-），男，博士，美国佛罗里达大学电气与计算机工程系教授，从事半导体、微纳机电系统（MEMS）等领域研究。

A Studyon the Convection Coefficient of an Electro-Thermal Bimorph Actuator*

LIU Junwen1，2，XU Dacheng1*，CHEN Qiao2，DING Jinling2，XIE Huikai3
（1.College of Electronics and Information Science，Soochow University，Suzhou 215000，China；2.WiO Technology Co.Ltd，Wuxi 214000，China；3.Department of Electrical and Computer Engineering，University of Florida 32611，Florida，USA）

A method of estimating the convection coefficient at microscale is presented in this paper，based on the modeling and experimental data of a microfabricated electrothermal bimorph actuator.In this method，an analytical heat transfer model of the electro-thermal bimorph actuator is established first.Then the model is used to analyze the temperature distribution and extract the convection coefficient from measurement data.The convection coefficient obtained by this method matches the experimental result within 8.1%，which validates the rationality of this method.

convection coefficient；electro-thermal Bimorph；micro-actuator；thermal resistance model

TP215；TK124

A

1004-1699（2015）08-1120-05

��2575；8460；7320R

10.3969/j.issn.1004-1699.2015.08.004

2015-03-19 修改日期：2015-05-29