短龄期再生混凝土三轴受压力学性能及其本构关系

陈宗平，应武挡，陈宇良，姚 侃

（1.广西大学 土木建筑工程学院，广西 南宁 530004；2.广西大学 工程防灾与结构安全教育部重点实验室，广西 南宁 530004；3.同济大学 建筑工程系，上海 200092）

随着城市建筑垃圾的累增，再生混凝土的相关性能已成为当前国内外研究的热点问题.再生混凝土是指将废弃混凝土经过破碎、筛分、清洗，并按一定比例和级配重新配制的混凝土.它能有效解决建筑垃圾处理的问题，实现建筑材料的循环利用，具有很好的应用前景.国内外学者［1－8］对再生混凝土的强度、弹性模量和断裂能等力学性能进行了深入研究，分析了再生粗骨料规格、取代率、原生混凝土强度以及骨料缺陷等因素对再生混凝土力学性能的影响，为再生混凝土的推广应用奠定了坚实基础.然而已有成果主要集中于再生混凝土在单轴应力状态下的力学性能方面，对其在复杂应力状态下力学性能的研究成果尚不多见.而实际工程中混凝土结构常处于复杂应力状态，如梁柱节点核心区混凝土、螺旋箍筋约束混凝土、钢管混凝土、大体积混凝土等，仅仅掌握单轴应力状态下再生混凝土的力学性能，尚不能满足工程应用的实际需求.此外，在实际工程中，迫于工期紧张、加快模板周转等现实需要，常在满足使用要求和承载力要求的条件下适当缩短混凝土结构的养护龄期，力求取得较好的经济效益.在30d的短龄期内再生混凝土力学性能如何变化，特别是其在三轴受压状态下承载能力及变形性能如何，目前在国内外文献中尚未见相关报道.为了丰富再生混凝土的研究内容并进一步推广其应用，本文以龄期和围压值为变化参数，设计了14个再生混凝土试件进行三轴受压试验，研究其力学性能及其本构关系.

1 试验

1.1 试验材料

再生粗骨料来源于某省级工程检测中心测试完毕的强度等级为C35的碎石类混凝土试块，经颚式破碎机破碎、筛分和清洗后获得，粒径为5～20mm，连续级配，堆积密度为1 270kg／m3，吸水率为3.18%（质量分数）；细骨料为中粗河砂；水泥采用42.5R 普通硅酸盐水泥；水为城市自来水.再生混凝土设计强度为C35，其配合比为m（水）∶m（水泥）∶m（砂）∶m（再生粗骨料）＝1.00∶2.50∶2.71∶5.77.

1.2 试件设计

以试件龄期（t）和围压值（σw）为变量，设计直径为100mm、高度为200mm 的圆柱体试件14个，各试件的设计参数见表1.

1.3 加载装置及加载制度

再生混凝土的三轴受压试验在中科院和SIMENS公司联合研发的RMT－201试验机上完成，采用荷载和位移混合控制的加载制度.首先按预定设计参数施加围压值（σw），并按与围压值1∶1的比例同步施加轴向荷载（σv），然后，保持围压值恒定（荷载控制），轴向荷载以0.01 mm／s的速率加载（位移控制），直到试件破坏.试件的受力模型如图1所示，其中σi为各试件对应的围压值.

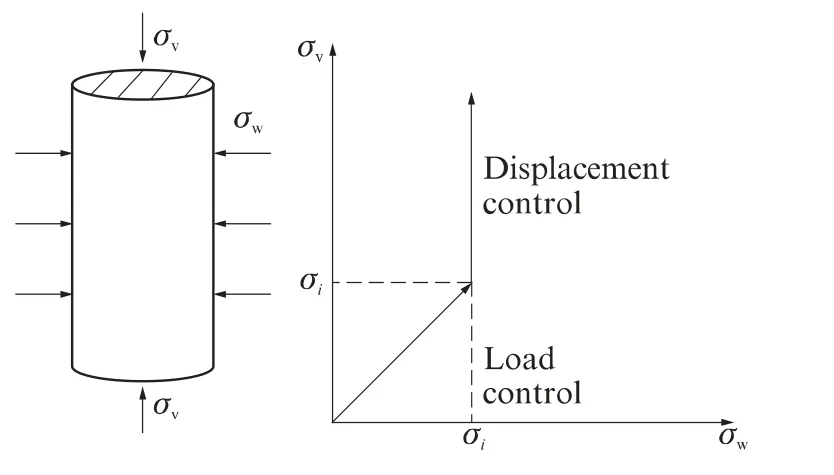
图1 试件受力模型Fig.1 Mechanical model of specimen

2 结果与分析

2.1 破坏形态

图2 试件的破坏形态Fig.2 Failure patterns of specimens

部分试件的破坏形态如图2所示.由图2可见：围压值σw＝0MPa时，破坏时试件中部出现多条竖向裂缝，其中1条或几条竖向裂缝贯穿试件两端；随着σw的增大，裂缝由竖向逐渐向斜向发展，当σw＝9MPa时，斜裂缝发展方向与水平方向呈60°～70°夹角；随着σw继续增大，夹角有微量减小的趋势；当σw＞6MPa时，斜裂缝贯穿整个试件，并出现少量的横向裂缝，裂缝两侧的混凝土相对剪切错开，并在试件中部局部鼓出，且σw越大，这种现象越为明显.通过对断裂界面的细致观察，发现再生粗骨料和水泥砂浆均为剪切破坏，局部出现压碎粉末.

2.2 轴向应力－应变曲线

图3为各试件的轴向应力－应变（σ－ε）曲线.各试件的峰值应力（σu）、峰值应变（εu）和弹性模量（E）等力学性能见表1.峰值应力和峰值应变取轴向应力－应变曲线最高点对应的应力、应变值；弹性模量取曲线在0.4σu处的割线模量.

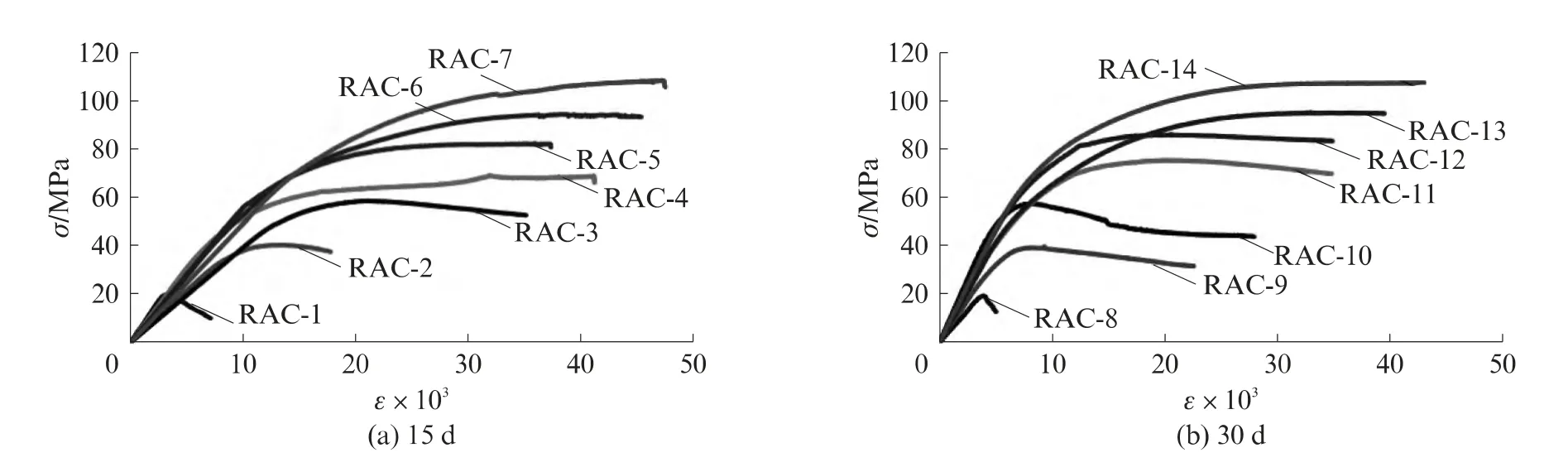
图3 试件的轴向应力－应变曲线Fig.3 Axial stress－strain curves of specimens

表1 试件的设计参数及力学性能Table 1 Designed parameters and mechanical properties of specimens

由图3和表1可见，随着围压值σw的变化，再生混凝土试件的轴向应力－应变曲线发生了显著的变化.σw为零时（即单轴受压状态下），试件的峰值应力、峰值应变和弹性模量均比有围压时的试件小，并且过峰值后曲线下降段陡峭；随着σw的增加，试件的峰值应力、峰值应变和弹性模量逐渐增大，特别是过峰值后曲线下降段有较为显著的变化；σw为3，6MPa时，曲线还存在下降段，σw达到9，12 MPa时，曲线过峰值后保持水平，几乎不再下降；σw为15，18MPa时，曲线一直上升，在应变达到40×10－3时，依然没有下降段，这说明围压能够显著改善再生混凝土的脆性.

由图3 和表1 还可见，σw相同时，龄期为15，30d再生混凝土试件的峰值应力、峰值应变相差不大，轴向应力－应变曲线走势也大致相同，但是龄期30d试件的轴向应力－应变曲线在初始阶段的斜率明显大于龄期15d的试件.

2.3 力学性能

2.3.1 龄期的影响

表2给出了不同围压值下再生混凝土30d峰值应力σu2和15d峰值应力σu1的比值（σu2／σu1）.由表2可见，σu2／σu1基本保持在1附近，这表明短龄期内龄期的变化对再生混凝土三轴受压时的极限承载力影响不大.这可能是由于受到围压的约束，再生混凝土试件的破坏形态发生了改变，不仅再生粗骨料和水泥浆体界面之间的黏结失效，而且再生粗骨料本身也被剪断；三轴受压强度的大小主要取决于再生粗骨料的抗剪能力，而短龄期对再生粗骨料本身的抗剪能力影响不大.

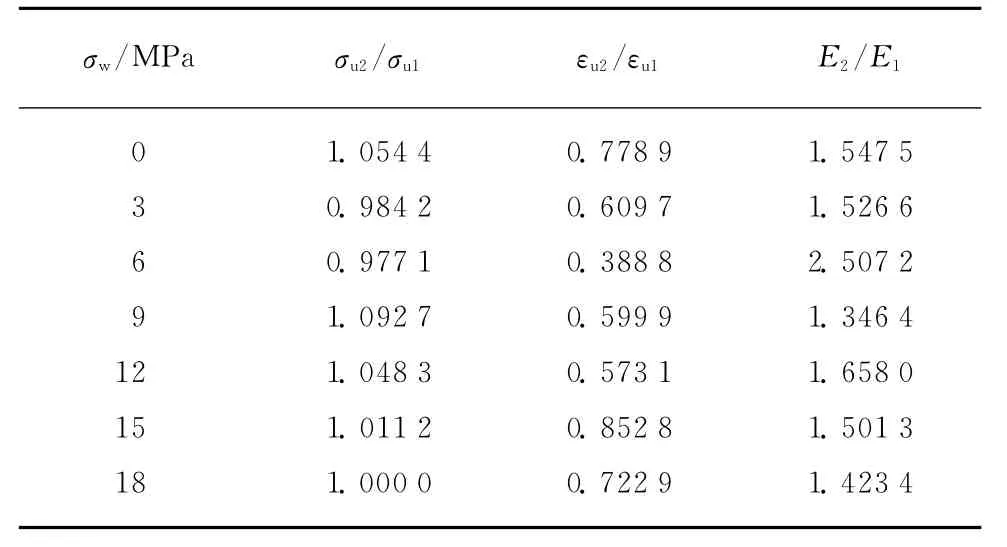
表2 不同龄期试件的力学性能比较Table 2 Mechanical properties comparison of specimens under different aging times

再生混凝土试件30d峰值应变εu2和15d峰值应变εu1的比值（εu2／εu1）见表2.由表2可见，试件30d峰值应变比15d峰值应变要小，其比值在0.6附近上下波动.这可能是由于随着龄期的适当延长，再生混凝土内部的水泥浆体水化反应更为充分，导致其更脆的缘故.

表2还给出了再生混凝土30d弹性模量E2和15d弹性模量E1的比值（E2／E1）.由表2可见，试件30d弹性模量普遍比15d弹性模量要大，其比值在1.5上下波动.

2.3.2 围压值的影响

不同围压值下，短龄期再生混凝土的15，30d峰值应力变化趋势基本一致.随着围压值的增大，再生混凝土的峰值应力基本呈线性上升的趋势.参照文献［9］的研究方法，结合实测值（见表1），利用围压值与轴向应力的关系确定再生混凝土峰值应力σu的计算公式为：

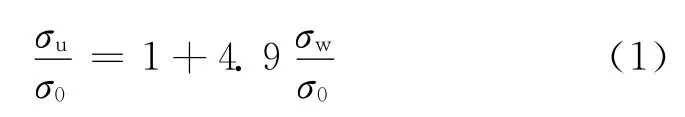
式中：σ0为围压值为零时（即单轴应力状态下）试件的峰值应力.计算值与实测值的相对误差在7%以内，表明该公式可用于三轴受压再生混凝土峰值应力的计算.

不同围压值下，短龄期再生混凝土的峰值应变变化趋势基本一致.随着围压值的增大，再生混凝土的峰值应变基本呈线性上升的趋势，但不同龄期试件峰值应变的上升速率不一致.根据表1的试验数据，拟合了不同龄期再生混凝土在不同围压值下峰值应变εu的计算公式：

式中：ε0为围压值为零时试件的峰值应变；α 为龄期的修正系数，龄期15，30d 时其值分别取1.2 和1.0.计算值与实测值的相对误差在6%以内.

随着围压值的增大，再生混凝土的弹性模量基本呈线性上升的趋势，但不同龄期试件弹性模量的上升速率不一致.根据表1 的试验数据，参照文献［10］的研究方法，拟合了不同龄期再生混凝土在不同围压值下弹性模量E 的计算公式：

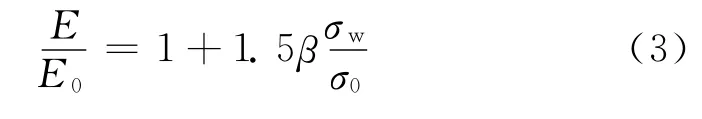
式中：E0为围压值为零时试件的弹性模量；β为龄期修正系数，龄期15，30d时其值分别取0.5和1.0.

3 再生混凝土的三轴受压强度计算

国内外学者［9－11］对普通混凝土的三轴受压强度计算方法进行了大量研究，并取得许多重要成果，部分成果已经应用到规范中［12－13］.本文尝试运用文献［12－13］的方法计算再生混凝土的三轴抗压强度，并与σu实测值进行对比分析，如表3所示.由表3可见：参照CEB－FIP（1990）方法的计算值σc1与实测值吻合较好；参照GB 50010—2010方法的计算值σc2比实测值小，偏于安全，并且随着围压值的增大，计算值与实测值的偏差越来越大，这可能是由于GB 50010—2010规范给出了最高强度的限制，且围压值越大，最高强度的限制效果越明显，从而导致偏差值较大的缘故.

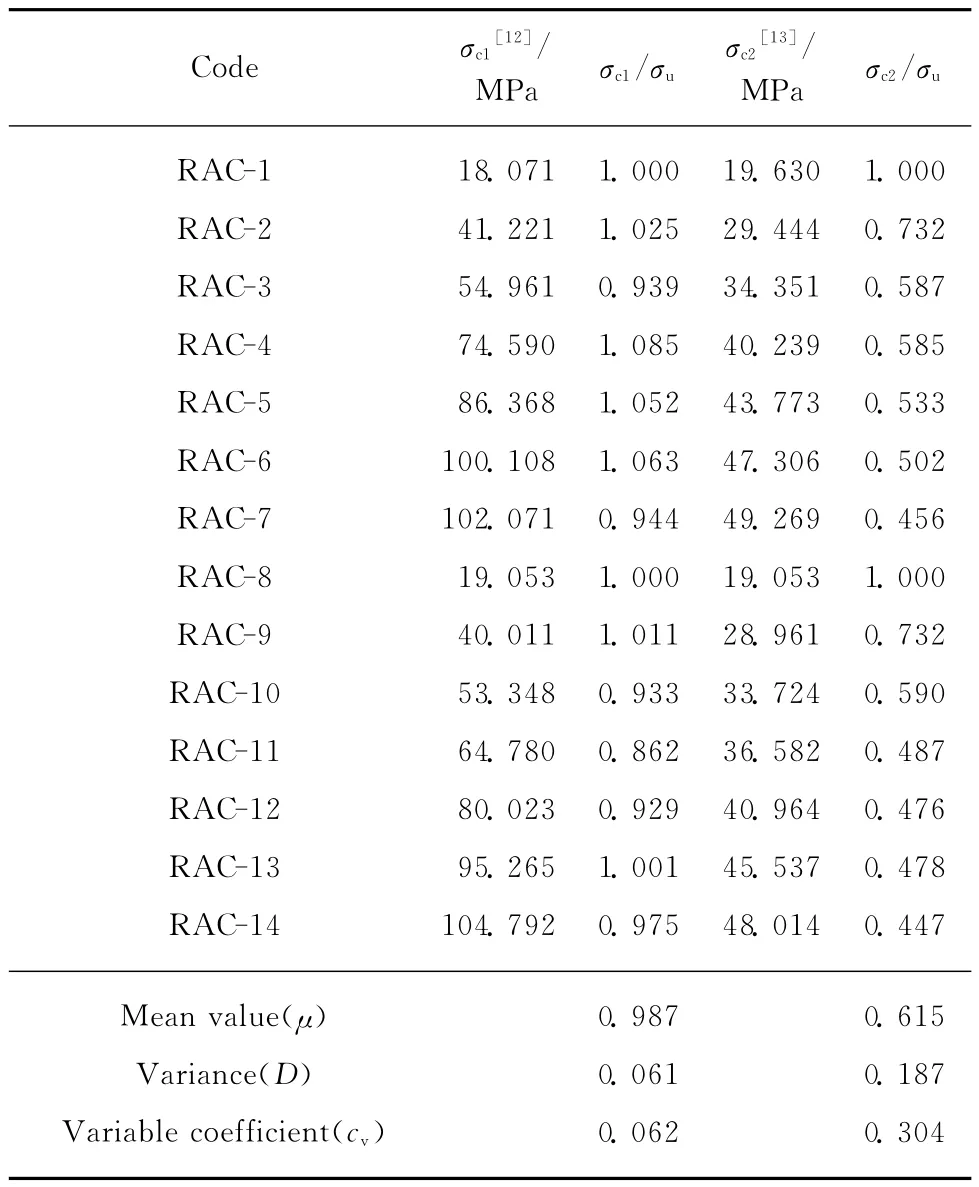
表3 计算值与实测值比较Table 3 Comparison between calculated results and experimental results

4 应力－应变本构方程

为方便再生混凝土三轴抗压性能的理论分析和工程应用，需确定其轴向应力－应变曲线的数学表达式.为消除变化参数的影响，以σ／σu为纵坐标，ε／εu为横坐标，给出归一化处理后的应力－应变曲线，见图4.龄期15，30d时的归一化应力－应变曲线形态相似，但其上升段的曲线斜率不同.参照文献［11］的研究方法，并考虑σw的影响，提出了以下分段式本构方程：

当围压值σw＝0MPa时：

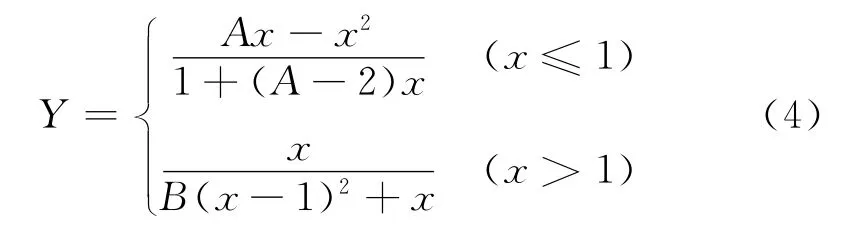
式中：Y＝σ／σu；x＝ε／εu；A，B 分别为曲线上升段和下降段的控制参数.龄期15 d 时，A＝1.1，B＝10.0；龄期30d时，A＝1.2，B＝8.5.

当围压值σw≠0MPa时：

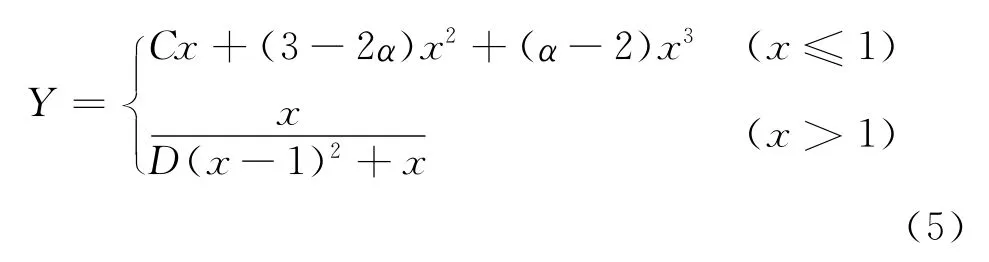
式中：C 为上升段参数，其计算公式见式（6）；D 为下降段参数，当曲线无明显下降时D 取0.1，其计算公式见式（7）.

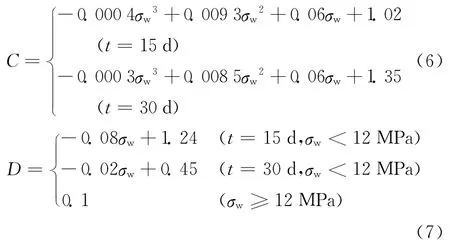
全部试件按式（4）～（7）拟合后的归一化应力－应变曲线如图4所示.由图4可见，除试件RAC－4（t＝15d，σw＝9 MPa）外，其余试件拟合得到的归一化应力－应变本构关系曲线均与试验结果吻合良好.

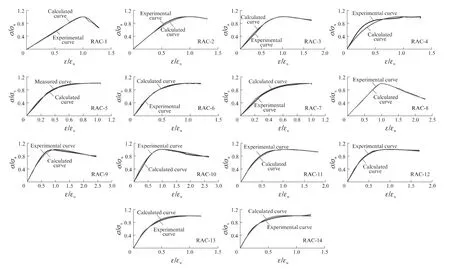
图4 试验与理论计算的归一化应力－应变曲线对比Fig.4 Comparison between calculated and experimental normalized stress－strain curves

5 结论

（1）围压能有效提高短龄期再生混凝土的峰值应力、峰值应变以及弹性模量.

（2）龄期从15d延长到30d时，再生混凝土的峰值应力变化不大，但其峰值应变减小，弹性模量变大.

（3）采用CEB－FIP（1990）中的方法，计算再生混凝土的三轴抗压强度，计算值与实测值吻合较好.采用GB 50010—2010中的方法，计算值比实测值小，偏于安全.

（4）基于试验数据建立了短龄期再生混凝土三轴受压状态下的应力－应变本构方程，以及不同围压值下各龄期再生混凝土的峰值应力、峰值应变和弹性模量的计算公式，计算值与实测值吻合较好，可供再生混凝土研究领域的强度计算、数值模拟分析和工程应用参考.

［1］ACHTEMICHUK S，HUBBARD J，SLUCE R，et al.The utilization of recycled concrete aggregate to produce controlled low－strength materials without using Portland cement［J］.Cement and Concrete Composites，2009，31（8）：564－569.

［2］ETXEBERRIA M，VAZQUEZ E，MARI A，et al.Influence of amount of recycled coarse aggregates and production process on properties of recycled aggregate concrete［J］.Cement and Concrete Research，2007，37（5）：735－742.

［3］POON C S，SHUI Z H，LAM L，et al.Influence of moisture states of natural and recycled aggregates on the slump and compressive strength of concrete［J］.Cement and Concrete Research，2004，34（1）：31－36.

［4］AMNON K.Properties of concrete made with recycled aggregate from partially hydrated old concrete［J］.Cement and Concrete Research，2003，33（5）：703－711.

［5］肖建庄，杜江涛.不同再生粗集料混凝土单轴受压应力－应变全曲线［J］.建筑材料学报，2008，11（1）：111－115.XIAO Jianzhuang，DU Jiangtao.Complete stress－strain curve of concrete with different recycled coarse aggregates under uniaxial compression［J］.Journal of Building Materials，2008，11（1）：111－115.（in Chinese）

［6］陈宗平，徐金俊，郑华海，等.再生混凝土基本力学性能试验及应力－应变本构关系［J］.建筑材料学报，2013，16（1）：24－32.CHEN Zongping，XU Jinjun，ZHENG Huahai，et al.Basic mechanical properties test and stress－strain constitutive relations of recycled coarse aggregate concrete［J］.Journal of Building Materials，2013，16（1）：24－32.（in Chinese）

［7］寇世聪，潘智生.不同强度混凝土制造的再生骨料对高性能混凝土力学性能的影响［J］.硅酸盐学报，2012，40（1）：7－11.KOU Shicong，PAN Zhisheng.Effect of quality of parent concrete on the mechanical properties of high performance recycled aggregate concrete［J］.Journal of the Chinese Ceramic Society，2012，40（1）：7－11.（in Chinese）

［8］朋改非，黄艳竹，张九峰.骨料缺陷对再生混凝土力学性能的影响［J］.建筑材料学报，2012：15（1），80－84.PENG Gaifei，HUANG Yanzhu，ZHANG Jiufeng.Influence of defects in recycled aggregate on mechanical properties of recycled aggregate concrete［J］.Journal of Building Materials，2012，15（1）：80－84.（in Chinese）

［9］闫东明，林皋，徐平.三向应力状态下混凝土动态强度和变形特性研究［J］.工程力学，2007，24（3）：58－64.YAN Dongming，LIN Gao，XU Ping.Dynamic strength and deformation of concrete in tri－axial stress states［J］.Engineering Mechanics，2007，24（3）：58－64.（in Chinese）

［10］过镇海，时旭东.钢筋混凝土原理和分析［M］.北京：清华大学出版社，2003：13－24.GUO Zhenhai，SHI Xudong.Reinforced concrete theory and analyse［M］.Beijing：Tsinghua University Press，2003：13－24.（in Chinese）

［11］LOKUGE W P，SANJAYAN J G，SETUNGE S.Stress－strain model for laterally confined concrete［J］.Journal of Materials in Civil Engineering，2005，17（6）：607－616.

［12］CEB－FIP Model code 1990：Design code［S］.

［13］GB 50010—2010 混凝土结构设计规范［S］.GB 50010—2010 Code for design of concrete structures［S］.（in Chinese）