基于BP神经网络的灌孔砌块砌体抗压强度预测

王凤来，朱 飞，周 强

（1.哈尔滨工业大学 结构工程灾变与控制教育部重点实验室，黑龙江 哈尔滨 150090；2.哈尔滨工业大学 土木工程学院，黑龙江 哈尔滨 150090）

灌孔配筋砌块砌体结构具有节能、节地、节水、节材、低碳等特征，在美国、新西兰等国家广泛应用［1］.灌孔配筋砌块砌体结构在国内的应用量已突破1×107m2，最高的试点工程为哈尔滨科盛大厦板式办公楼，主体高度98.8m，28层［2］.灌孔砌块砌体抗压强度是灌孔配筋砌块砌体结构的基本力学性能指标.影响灌孔砌块砌体抗压强度的因素包括砌块、砂浆、灌孔混凝土的抗压强度、变形性能及其界面相互作用、灌孔混凝土面积与砌体毛截面面积比值（α）、砌块块型和施工质量等［1］.各影响因素之间关系复杂，使灌孔砌块砌体表现为各向异性且单轴抗压强度试验数据离散性较大.

既有的灌孔砌块砌体抗压强度计算方法可分为两类［3］：第一类是理论推导方法，主要包括弹性理论分析法、变形协调分析法和强度破坏理论分析法等［4］，例如Priestley［5］、刘桂秋［6］和GB 50003—2011《砌体结构设计规范》均依据简化力学模型提出了灌孔砌块砌体抗压强度计算公式，并利用试验数据标定计算公式中的待定参数，Hasan等［7］考虑复杂应力状态发展了用于灌孔砌块砌体抗压强度计算的弹性有限元分析方法；第二类是数理统计方法，该方法忽略了试验中各组成材料的相互作用，通过大量的试验数据，对灌孔砌块砌体抗压强度进行统计分析或结合经典理论提出用于灌孔砌块砌体抗压强度计算的半理论半经验公式，例如Khalaf等［8］、黄靓等［1］均采用数理统计方法提出了灌孔砌块砌体抗压强度的计算公式.然而，尽管各研究者提出了不同的灌孔砌块砌体抗压强度计算模型，但各模型之间预测结果的准确性并未得到比较；GB 50003—2011规范中的灌孔砌块砌体抗压强度计算公式不适用于砂浆抗压强度高于砌块抗压强度的情况，若砂浆抗压强度高于砌块抗压强度，灌孔砌块砌体抗压强度计算公式将无法运算；Paulay等［9］和孟凡晓等［10］在确定灌孔砌块砌体抗压强度中均忽略了砂浆抗压强度的作用，该方法的合理性尚需大量试验结果进行验证.

BP神经网络作为数理统计方法的一种，已成功应用于预测不同配合比下的混凝土抗压强度和既有建筑中的混凝土强度等［11－12］.BP神经网络是由神经单元互相连接而形成的非线性动力学系统，具有非线性自适应的信息处理能力［13］.鉴于BP 神经网络具有高效处理多参数影响的优势，本文将通过BP神经网络建立灌孔砌块砌体抗压强度计算模型.

1 试验概况及灌孔砌块砌体实测抗压强度

进行了5组共36件灌孔砌块砌体的抗压强度试验.试件的设计和施工依据GB／T 50129—2011《砌体基本力学性能试验方法标准》进行.试件尺寸为1 000mm（高）×590mm（宽）×190mm（厚）.试验所用材料为孔洞率（体积分数）46%的普通混凝土小型空心砌块、砂浆和灌孔混凝土.试件砌筑在找平的木模底板上，砌筑过程中需控制灰缝厚度及试件平整度.试件砌筑完毕后养护7d，然后进行混凝土灌孔（灌孔率（体积分数）为100%）并振捣充分.抗压强度试验之前，试件表面采用专用找平仪进行石膏找平以控制其承载面间的平行度.参数α 值及砌块抗压强度f1、砂浆抗压强度f2、灌孔混凝土抗压强度fc见表1.试验采用10 000kN 电液伺服压力机进行加载，加载装置如图1所示.

图1 加载装置Fig.1 Set up for loading

灌孔砌块砌体实测抗压强度（fgm）见表1.

表1 灌孔砌块砌体实测抗压强度Table 1 Tested compressive strength of grouted block masonry

2 既有研究抗压强度试验数据统计

统计了既有研究［10，14－25］中139组共530件 灌孔砌块砌体的抗压强度试验数据，结果见表2.

对表1，2中各参量的变化范围合并（共144组）统计，结果见表3.

3 BP神经网络模型

3.1 BP神经网络原理

BP神经网络模型是目前应用最广泛的人工神经网络模型之一.BP神经网络是一种多层前馈神经网络，包含输入层，隐含层和输出层，每层由若干节点组成，每个节点具有特定的激励函数，不同层的节点间均有信息交换，信号由权函数传递，但同一层的节点间无信息传输.BP神经网络算法是信号向前传递，误差反向传播，即输入信号从输入层经隐含层逐层处理，直至输出层，然后通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小［25］.典型的3层BP神经网络结构如图2所示.

表2 既有研究灌孔砌块砌体抗压强度试验数据统计Table 2 Data statistics of compressive strengths of grouted block masonry in existing researches

表3 参量变化范围统计Table 3 Statistics of change ranges of parameters

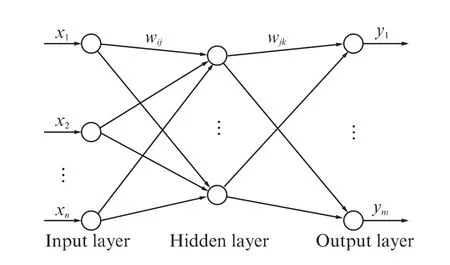
图2 典型的3层BP神经网络结构Fig.2 Typical three－layer BP neural network structure

BP神经网络的训练过程［26］如下：

（1）根据系统要求确定输入层节点数n、隐含层节点数l、输出层节点数m、输入层矩阵X 和输出矢量T.

（2）根据第i个输入层输入xi、输入层与隐含层权值wij以及隐含层阈值aj，计算第j个隐含层输出yj.

式中：fj为第j 个隐含层激励函数.

（3）根据第j个隐含层输出yj、隐含层与输出层权值wjk和输出层阈值bk，计算第k 个输出层输出yk.

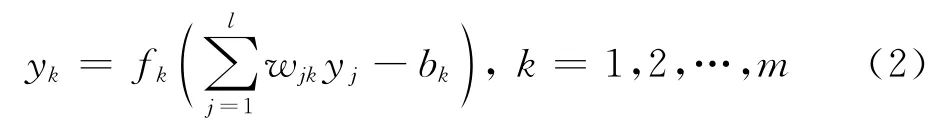
式中：fk为第k 个输出层激励函数.

（4）根据输出矢量T 和预测输出Y，计算网络预测误差E.

式中：tk为第k 个输出节点的期望输出.

（5）计算隐含层与输出层权值增量Δwjk及输出层阈值增量Δbk.

式中：η为学习速率；δjk＝（tk－yk）代表激励函数fk的一阶导数.

（6）计算输入层与隐含层权值增量Δwij和隐含层阈值增量Δaj.

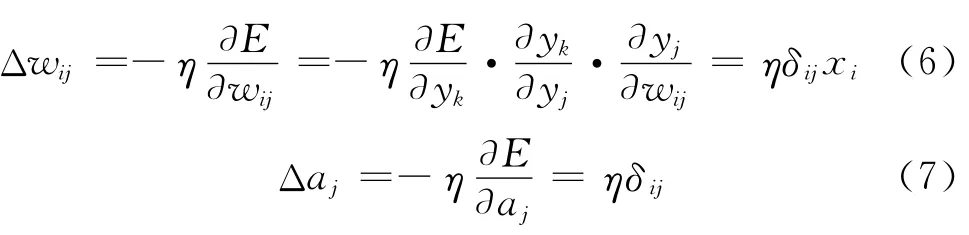
式中：δij为输入层与隐含层之间的学习规则系数.

（7）根据网络预测误差E 是否满足预期精度要求，判断BP神经网络算法迭代是否结束.若没有结束，返回步骤（2），再重复计算直至网络预测误差E达到最小.

3.2 用于抗压强度预测的BP神经网络建立

设计BP 神经网络采用4 个参数的输入，分别为灌孔混凝土面积与砌体毛截面面积比值（α）、砌块抗压强度（f1）、砂浆抗压强度（f2）、灌孔混凝土抗压强度（fc），输出层为1个参数，即灌孔砌块砌体抗压强度（fgm），并设置1 个隐含层.依据Kolmogorov定理，在BP神经网络构建中，若输入层节点数为n，则隐含层节点数可取为2n＋1.为比较隐含层节点数对BP神经网络预测结果的影响并简化分析，分别取隐含层节点数为1，3，5，7，9进行训练.

采用MATLAB 人工神经网络工具箱编程计算，具体步骤如下：

（1）建立BP神经网络.将144组试验数据采用式（8）进行归一化处理［3］.

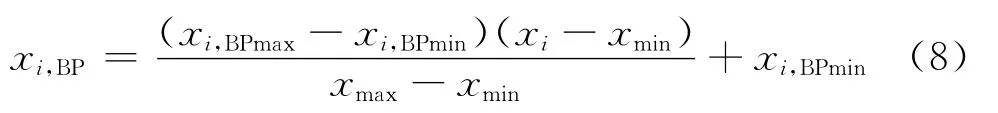
式中：xi，BP为归一化数据；xi为试验数据原始值；xmax为试验数据最大值；xmin为试验数据最小值；xi，BPmin为归一化数据最小值；xi，BPmax为归一化数据最大值.当输入和输出数据归一化至［－1，1］时，xi，BPmin＝－1，xi，BPmax＝1，则式（8）可简化成xi，BP＝

随机选取120 组归一化数据作为网络学习样本，其余24组的归一化数据作为网络测试样本.依据学习样本建立三层BP 神经网络模型.隐含层激励函数为Sigmoid型对数函数f（x）＝1／（1＋e－x），输出层激励函数为线性函数.采用Levenberg－Marquardt算法，训练次数为1 000 次，学习速率为0.05［12］.

（2）计算BP神经网络预测值.将测试样本输入层数据代入BP神经网络，计算出BP神经网络的预测值.

（3）计算归一化数据与BP 神经网络预测值之比.将测试样本输出层数据（归一化的灌孔砌块砌体抗压强度试验值）除以BP 神经网络预测值并取其平均值，评价BP神经网络预测结果的准确性.

（4）BP神经网络预测结果稳定性.考虑到样本容量较大且网络学习样本数据选择的随机性，进行10次计算以检验测试样本输出层数据与BP神经网络预测值比值的稳定性.

BP神经网络预测结果稳定性见表4.

表4 BP神经网络预测结果稳定性Table 4 Stability of predicted results of BP neural network

由表4可知，当隐含层包含7 个节点时，10 次计算后测试样本输出层数据与BP 神经网络预测值比值的极差和标准差均最小，稳定性最好，平均值为1.011，预测结果较准确.表明在统计的144组抗压强度试验样本空间内，采用BP 神经网络建立的非线性系统可以良好地预测影响因素复杂的灌孔砌块砌体的抗压强度.

4 简化的抗压强度计算公式推导

尽管建立的隐含层为7个节点的BP 神经网络模型在预测灌孔砌块砌体抗压强度时最稳定，但隐含层仅有1个节点的10次计算后测试样本输出层数据与BP神经网络预测值比值的平均值为1.016，标准差为0.054（见表4），因此可通过隐含层为1个节点的BP神经网络建立简单的灌孔砌块砌体抗压强度计算公式.此时输入层与隐含层权值矩阵维数为1×4，隐含层与输出层权值及隐含层、输出层阈值均为标量.

（1）依据隐含层和输出层的激励函数形式，确定简化的灌孔砌块砌体抗压强度表达式，为：

（2）进行1次隐含层为1个节点的BP神经网络训练，归一化处理后，得到测试样本输出层数据与BP神经网络预测值比值的平均值为1.012，标准差为0.196.此时对应的H＝［0.196 4 0.044 9 0.714 4 1.936 2］，G ＝［2.364 9］，a1＝［－0.813 2］，b2＝［－0.837 5］.

（3）应用式（8）求逆，然后结合表3中各参数的取值范围，将式（9）反归一化，再代入算例中求权值与阈值，得：

5 既有灌孔砌块砌体抗压强度计算公式对比分析

新西兰砌体规范［22］考虑了砌块抗压强度、灌孔混凝土抗压强度和α对灌孔砌块砌体抗压强度的影响，同时忽略了砂浆抗压强度的贡献，即：

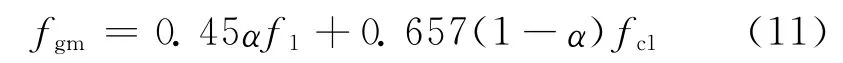
式中：fc1为直径200mm、高100mm 的圆柱体混凝土试件的抗压强度.

GB 50003—2011规范基于变形协调分析，采用应力叠加法推导简化，将灌孔砌块砌体抗压强度表达为空心砌体抗压强度（fm）与灌孔混凝土抗压强度的线性叠加（见式（12）），并将空心砌体抗压强度表达为砌块抗压强度与砂浆抗压强度的非线性组合（见式（13））.式（13）仅适用于砂浆抗压强度不高于砌块抗压强度的情况.灌孔砌块砌体抗压强度中灌孔混凝土抗压强度贡献受到α 的影响，要求砌块砌体灌孔率不小于33%.

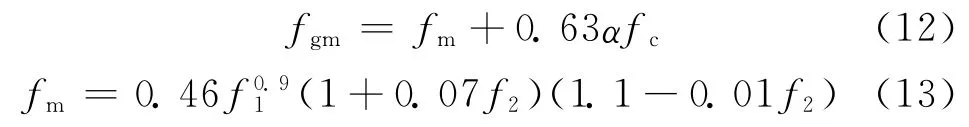
刘桂秋［6］基于弹性理论分析法，假定砌体受压破坏前，砌块、砂浆及灌孔混凝土均为匀质弹性材料，采用Hilsdorf砌体破坏准则反映灌孔砌块砌体在双向拉压应力状态下的破坏，提出灌孔砌块砌体抗压强度公式，为：

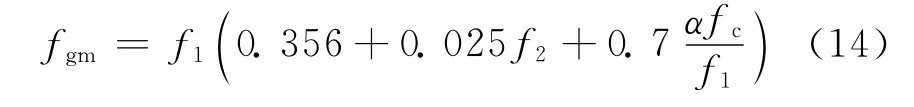
Hasan等［7］通过弹性有限元法分析获得灌孔砌块砌体抗压强度表达式，为：

Paulay等［9］采用强度破坏理论分析方法，基于改进的Hilsdorf砌体破坏准则，同时忽略了砂浆抗压强度对灌孔砌块砌体抗压强度的贡献，将灌孔砌块砌体抗压强度表达为砌块抗压强度和灌孔混凝土抗压强度的非线性组合.

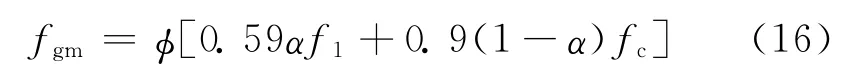
式中：φ 为修正系数.当φ 取1.0时，fgm为灌孔砌块砌体抗压强度平均值；当φ 取0.75时，fgm为灌孔砌块砌体抗压强度设计值.

黄靓等［1］采用半理论半经验方法，依据既有灌孔砌块砌体抗压强度计算公式（式（17），（18）），进行较低砂浆抗压强度的灌孔砌块砌体抗压强度计算.

孟凡晓等［10］通过22个高强灌孔砌块砌体抗压强度试验，认为砂浆抗压强度对灌孔砌块砌体抗压强度影响不明显，只需考虑砌块抗压强度和灌孔抗压强度的影响.他们以式（12）为基础，拟合出灌孔砌块砌体抗压强度计算公式，为：

Khalaf等［8］通过试验统计分析，将灌孔砌块砌体抗压强度表达为砌块抗压强度、砂浆抗压强度和灌孔混凝土抗压强度的线性叠加，未计入砌块空心率及混凝土灌孔率的影响.灌孔砌块砌体抗压强度计算公式为：

灌孔砌块砌体抗压强度试验值与各公式计算值比值R（平均值）见表5.

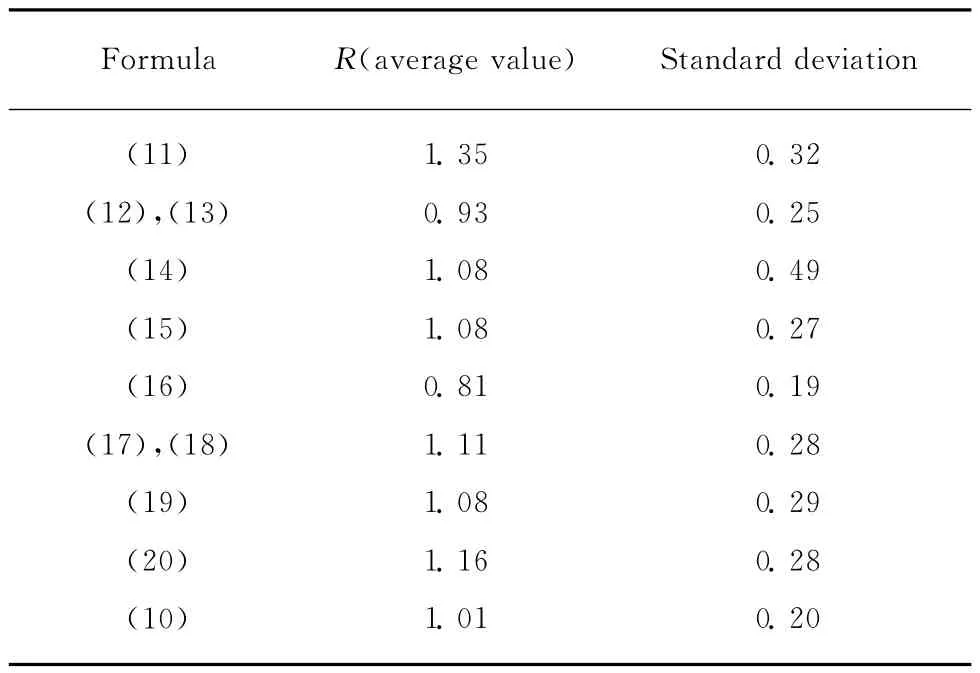
表5 灌孔砌块砌体抗压强度试验值与各公式计算值比值Table 5 Ratio（R）of test data and calculated data of compressive strength of grouted block masonry

由表5可见，灌孔砌块砌体抗压强度试验值与式（12），（13），（16）计算值比值（平均值）均小于1.0，标准差均≤0.25，表明式（12），（13），（16）的计算结果偏于不保守；灌孔砌块砌体抗压强度试验值与式（19）计算值比值（平均值）为1.08，标准差为0.29，表明采用式（19）对灌孔砌块砌体抗压强度进行预测可取得较优的结果.

灌孔砌块砌体抗压强度试验值与式（20）计算值比值（平均值）为1.16，标准差为0.28.与同为依据数理统计方法建立的式（17），（18），（19）相比，式（20）预测结果整体稳定性相近，但抗压强度计算值相对较低，因此，未考虑砌块空心率及混凝土灌孔率的影响，将灌孔砌块砌体抗压强度简化为砌块抗压强度、砂浆抗压强度和灌孔混凝土抗压强度的线性叠加有所不妥.

在忽略砂浆抗压强度影响的计算公式中，尽管式（16）对灌孔砌块砌体抗压强度的计算结果有最小的标准差（0.19），但式（16）计算所得的灌孔砌块砌体抗压强度偏大（R 为0.81（平均值）），而式（11）对灌孔砌块砌体抗压强度的计算结果有较大的标准差（0.32），并且式（11）计算所得的灌孔砌块砌体抗压强度偏小（R 为1.35（平均值）），这表明采用忽略砂浆抗压强度影响的计算公式对灌孔砌块砌体抗压强度进行预测将产生明显的误差，因此灌孔砌块砌体抗压强度计算公式中应计入砂浆抗压强度的影响才可获得与试验结果更相近的抗压强度计算值.

灌孔砌块砌体抗压强度试验值与式（10）计算值比值（平均值）为1.01，标准差仅为0.20，表明简化的抗压强度计算公式（式（10））可以良好地预测灌孔砌块砌体的抗压强度，且保持良好的稳定性.式（10）可用于式（12），（13）计算结果的验证.另外，式（10）还适用于砂浆抗压强度不小于砌块抗压强度的灌孔砌块砌体抗压强度的计算.

6 结论

（1）隐含层包括7 个节点的三层BP 神经网络的仿真效果最好，10次计算后测试样本输出层数据与BP神经网络预测值比值的平均值为1.011，标准差为0.041.

（2）灌孔砌块砌体抗压强度试验值与式（10）计算值比值（平均值）为1.01，标准差为0.20，表明在统计样本空间内，简化的灌孔砌块砌体抗压强度计算公式预测结果良好，稳定性优良，因此该计算公式可用于灌孔砌块砌体抗压强度的计算.

［1］黄靓，王辉，陈胜云.低强度砂浆灌孔砌块砌体抗压性能试验研究［J］.工程力学，2012，29（10）：157－161.HUANG Liang，WANG Hui，CHEN Shengyun.Experimental research on compressive behavior of grouted block masonry with low－strength mortar［J］.Engineering Mechanics，2012，29（10）：157－161.（in Chinese）

［2］王凤来，朱飞，孙绪杰.配筋砌块砌体剪力墙结构在超高层办公建筑中的应用［C］∥第22届全国结构工程会议论文集.乌鲁木齐：工程力学杂志社，2013：433－437.WANG Fenglai，ZHU Fei，SUN Xujie.The applications of reinforced concrete block masonry shear wall structures in highrise office buildings［C］∥Proceedings of the Twenty－Second National Conference on Structural Engineering.Urumqi：Engineering Mechanics Press，2013：433－437.（in Chinese）

［3］JULIO G R，CREU O M，JOSE M A.Compressive strength of masonry made of clay bricks and cement mortar：Estimation based on neural networks and fuzzy logic［J］.Engineering Structures，2013，48：21－27.

［4］吕伟荣.砌体基本力学性能及高层配筋砌块砌体剪力墙抗震性能研究［D］.长沙：湖南大学，2007.LU Weirong.The research on the basic mechanics performances of masonry and seismic behaviors of reinforced concrete masonry shear wall of tall buildings［D］.Changsha：Hunan University，2007.（in Chinese）

［5］PRIESTLEY M N J.Seismic design of concrete masonry shear walls［J］.ACI Journal，1986，83（1）：58－68.

［6］刘桂秋.砌体结构基本力学性能的研究［D］.长沙：湖南大学，2005.LIU Guiqiu.Research on basic mechanical properties of masonry structure［D］.Changsha：Hunan University，2005.（in Chinese）

［7］HASAN O K，CENGIZ K，HAKKI Y.Compression behavior and failure mechanisms of concrete masonry prisms［J］.ASCE，2005，17（1）：107－115.

［8］KHALAF F M，ARNOLD H W，DANIEL R F.Study of the compressive strength of blockwork masonry［J］.ACI Structural Journal，1994（4）：367－375.

［9］PAULAY T，PRIESTLEY M J N.Seismic design of reinforced concrete and masonry buildings［M］.New Jersey：John Wiley ＆Sons，Inc.，1992：106－114.

［10］孟凡晓，祝英杰，臧晓光，等.高强混凝土空心砌块砌体基本力学性能研究［J］.青岛理工大学学报，2007，28（1）：10－13.MENG Fanxiao，ZHU Yingjie，ZANG Xiaoguang，et al.Properties of high－strength concrete small－sized hollow block masonry［J］.Journal of Qingdao Technological University，2007，28（1）：10－13.（in Chinese）

［11］季韬，林挺伟，林旭健.基于人工神经网络的混凝土抗压强度预测方法［J］.建筑材料学报，2005，8（6）：677－681.JI Tao，LIN Tingwei，LIN Xujian.Prediction method of concrete compressive strength based on artificial neural network［J］.Journal of Building Materials，2005，8（6）：677－681.（in Chinese）

［12］尤杰，车轶，仲伟秋.基于BP 神经网络的既有建筑混凝土强度预测［J］.建筑科学与工程学报，2011，28（1）：70－75.YOU Jie，CHE Yi，ZHONG Weiqiu.Prediction of concrete strength of existing buildings based on BP neural networks［J］.Journal of Architecture and Civil Engineering，2011，28（1）：70－75.（in Chinese）

［13］郑君里，杨行峻.人工神经网络［M］.北京：高等教育出版社，1992：15－30.ZHENG Junli，YANG Xingjun.Artificial neural network［M］.Beijing：Higher Education Press，1992：15－30.（in Chinese）

［14］程才渊，吴明舜，孙恒军.混凝土小砌块灌孔砌体抗压及弹性模量试验研究［J］.四川建筑科学研究，2003，29（1）：56－59.CHENG Caiyuan，WU Mingshun，SUN Hengjun.Experimental research on the compressive strength and elastic modulus of grouted masonry［J］.Building Science Research of Sichuan，2003，29（1）：56－59.（in Chinese）

［15］杨伟军.混凝土砌体配筋剪力墙研究及砌体结构可靠性分析［D］.长沙：湖南大学，2000.YANG Weijun.Research on concrete masonry and reinforced masonry shear wall and reliability analysis of masonry structures［D］.Changsha：Hunan University，2000.（in Chinese）

［16］施楚贤，谢小军.混凝土小型空心砌块砌体受力性能［J］.建筑结构，1999，29（3）：10－12.SHI Chuxian，XIE Xiaojun.Mechanical behavior of concrete small sized hollow bock masonry［J］.Building Structure，1999，29（3）：10－12.（in Chinese）

［17］祝英杰.高强混凝土砌块砌体基本力学性能的试验研究及其动力分析［D］.沈阳：东北大学，2001.ZHU Yingjie.Experiment study on mechanical properties of masonry walls with high strength small size concrete hollow blocks and dynamic analysis［D］.Shenyang：Northeastern University，2001.（in Chinese）

［18］江波.高强砌块填芯砌体基本力学性能试验研究［D］.哈尔滨：哈尔滨建筑大学，2000.JIANG Bo.Experiment study on compressive behaviors of high strength grouted masonry［D］.Harbin：Harbin University of Civil Engineering ＆Architecture，2000.（in Chinese）

［19］张云杰.混凝土砌块砌体轴压应力应变关系试验研究［D］.哈尔滨：哈尔滨工业大学，2002.ZHANG Yunjie.Experimental research on the stress－strain curve of concrete block masonry［D］.Harbin：Harbin Institute of Technology，2002.（in Chinese）

［20］全成华.配筋砌块砌体剪力墙静动力性能研究［D］.哈尔滨：哈尔滨建筑大学，2002.QUAN Chenghua.Reinforced block masonry shear wall static and dynamic performance research［D］.Harbin：Harbin University of Civil Engineering ＆Architecture，2002.（in Chinese）

［21］宋力.混凝土砌块砌体基本力学性能试验研究与非线性有限元分析［D］.长沙：湖南大学，2005.SONG Li.Experimental study on basic mechanical behavior and non－linear FEA of concrete block masonry［D］.Changsha：Hunan University，2005.（in Chinese）

［22］NZS 4230 Design of reinforced concrete masonry structures［S］.

［23］张旭伟.非标砌块灌孔砌体抗压性能试验研究［D］.哈尔滨：哈尔滨工业大学，2009.ZHANG Xuwei.Experimental research on the compressive performance of grouted non－standard concrete block masonry［D］.Harbin：Harbin Institute of Technology，2009.（in Chinese）

［24］张宇.240、290宽砌块整浇墙标准抗压试验研究［D］.哈尔滨：哈尔滨工业大学，2010.ZHANG Yu.Experimental study on compressive property of grouted concrete 240and 290 block masonry［D］.Harbin：Harbin Institute of Technology，2010.（in Chinese）

［25］梁建国，龙腾.灌孔混凝土砌块砌体受压力学模型及其弹性模量［J］.工程力学，2012，29（7）：228－234.LIANG Jianguo，LONG Teng.Mechanical model and elastic modulus of grouted concrete block masonry in compression［J］.Engineering Mechanics，2012，29（7）：228－234.（in Chinese）

［26］宋玉普.混凝土的动力本构关系和破坏准则（下）［M］.北京：科学出版社，2013：95－112.SONG Yupu.Dynamic constitutive relation and failure criterion of concrete（volume two）［M］.Beijing：Science Press，2013：95－112.（in Chinese）