MVA与试卷统计分析方法评价课程教学质量

2015-11-27杨涵崧朱永长李国晶王涛赵淑金

经济师 2015年10期

杨涵崧朱永长李国晶王涛赵淑金

摘要：多变异分析方法是用来分析工序过程质量特征值变异规律的，文章将多变异分析模型和试卷统计分析方法应用于专业课教学质量评价中。班级间差异、学生间差异、课程内容间差异是影响课程教学质量的变异因素。通过对三种变异的分析，找出变异的因素，给分析和控制变异指明方向，为采取有效措施减少变异，得出科学的质量数据，为提高课程教学质量提供依据。

关键词：多变异分析统计分析教学质量方差分析

中图分类号：F222 文献标识码：A

文章编号：1004-4914（2015）10-226-03

从统计质量管理的角度来看，工序质量的连续改进过程就是不断地发现产品/工序质量变异并逐步减少变异的过程。多变异分析方法（multi-variant analysis，MVA）是用来分析工序过程质量特征值变异规律的一种重要方法。在工序能力分析、设计控制图和试验设计之前都采用MVA的方法确定影响产品质量特征值的变异来源。

对高校而言，学生就是高校的“产品”，培养学生成为合格的“产品”是一个庞大的系统工程。而教学工作是高校培养学生最重要而基本的工作，教学质量直接影响学生质量，教学过程就是培养合格产品的过程。在教学过程中，同一专业中存在着班级与班级之间的变异，学生个体之间的变异，每个学生对不同课程接受程度的变异，同一课程不同章节内容的变异。

研究中采用多变异分析方法（MVA）用于分析课程教学质量时发现，该模型可以有效确定影响课程教学质量的变异因素，但教学班学生整体对课程掌握的程度、与课程期望值的差异、成绩的分布是无法表现出来的。笔者尝试将多变异分析方法（MVA）与佳木斯大学试卷分析统计评价方法整合起来，共同用于教学质量评价，找出变异产生的原因，分析发生质量问题的根源，提出相应改进和提高的措施，以达到控制教学过程和教学质量的目的。

一、课程教学质量分析模型的建立

（一）课程教学质量试卷分析统计评价模型

试卷分析统计采取全面调查，确保数据普遍性与全面性，包括课程期望值、试卷平均值、偏差等主要内容。

课程的期望值E（X），公共基础和专业基础课E（X）=75，专业课E（X）=78。

试卷平均值X= Xi

标准差S=

偏差 -E（X）

利用上述试卷分析统计模型确定课程教学效果、学生对课程掌握的程度、与课程期望值的差异等信息。

（二）课程教学质量多变异分析模型

课程教学质量多变异分析采取抽样调查，抽样方式为等距抽样，操作简单易行。

多变异的分析问题可以看成一种随机效应的嵌套性实验。建立一定的线性统计模型，并假定各种变异效应相互独立，且不存在交互影响，以此前提下利用统计学方法进行方差分析。

MVA将工序质量特征值的变异分为三类：产品内变异、产品间的变异和时间变异。产品内的变异是指生产出的单位产品，其质量特征值在不同位置上所存在的差异。产品间变异是指从工序上连续抽检的两件产品，两件产品的质量特征值的均值间所存在的差异。从不同时间点抽取样品，观察其在不同时间的差异，称为时间变异。通过对三种变异的分析，可以发现哪种变异是显著的变异，从而为分析和控制变异指明了方向。

专业课程教学工作是高校学生学习专业知识的基本单元，影响课程教学质量的变异有不同班级间的差异（班级间变异）、同一班级内不同学生之间的差异（学生间变异）、每名学生对同一课程不同内容接受和掌握程度的差异（课程内容间变异）等三种。其关系如图1所示。通过对这三种变异的分析，找出哪种变异是显著的变异，从而为分析和控制变异指明方向，进而对某一专业课程的教学质量、学生综合素质与能力进行质量分析，得出科学的质量数据。

各测量点观测值见图2：

观测值Y1，1，1 Y1，2，1…Y1，b，1 Y2，1，1Y2，2，1…Y2，b，1 Ya，1，1Ya，2，1…Ya，b.1Y1，1，2 Y1，2，2…Y1，b，2 Y2，1，2Y2，2，2…Y2，b，2 Ya，1，2Ya，2，2…Ya，b.2Y1，1，n Y1，2，n…Y2，b，n Y2，1，nY2，2，n…Y2，b，n Ya，1，nYa，2，n…Ya，b，n

图2 教学质量的三种变异的观测值

由图2，模型表示第i个班级第j名学生第k个课程内容的学习成绩采样值：

Yi，j，k=μ+τi+βj（i）+εjk（i）～N（μ，σ2）（1）

上式中，μ为不考虑三种变异时的均值;σ2为不考虑三种变异时的方差;τi为班级间变异的影响;τi～N（0，στ2），（i=1，2，3，…a）;βj（i）为同一班级不同学生间变异的影响;βj（i）～N（0， σβ2），（j=1，2，3，…b）;εjk（i）为同一名学生对同一课程不同内容的变异影响，εjk（i）～N（0，σε2），（k=1，2，3，…n）。

上述三种变异相互独立，无交互作用，总方差为：

σ2=σε2+σβ2+σε2（2）

令Y= ;Y= ;Yi，j=

则总离差平方和为：

SSTOTAL= （Yi，j，k-Y）2= [（Yi-Y）+（Yi，j-Yi）+（Yi，j，k-Yi，j）]2

=bn （Yi-Y）2+n （Yi，j-Yi）2+ （Yi，j，k-Yi，j）2

=SSτ+SSβ+SSε（3）

（3）式中，第一項SSτ=bn （Yi-Y）2表示不同班级间离差平方和，其自由度为（a-1）;第二项SSβ=n （Yi，j-Yi）2表示同一班级内不同学生间的离差平方和，其自由度为a（b-1）;第三项SSε= （Yi，j，k-Yi，j）2表示同一学生对同一课程不同内容间的离差平方和，其自由度为ab（n-1）。

离差平方和公式的每一项除以它的自由度，结果就是每一项的均方差，两个均方差之比服从F分布。其方差分析表整理成表1。

各变异影响的均方差期望为：

E[MSτ]=bnστ2+nσβ2+σε2（4）

E[MSβ]=nσβ2+σε2（5）

E[MSε]=σε2（6）

各变异的方差估计为：

στ2= （7）

σβ2= （8）

σε2=MSε（9）

由于方差不可能是负数，当στ2或σβ2为负数时，按方差为零处理。

二、试卷统计分析与多变异分析模型对课程教学质量的应用

分析数据采集于佳木斯大学2011级无机非金属材料专业在2013年秋季学期进行的专业核心基础课——无机材料科学基础的考试成绩。

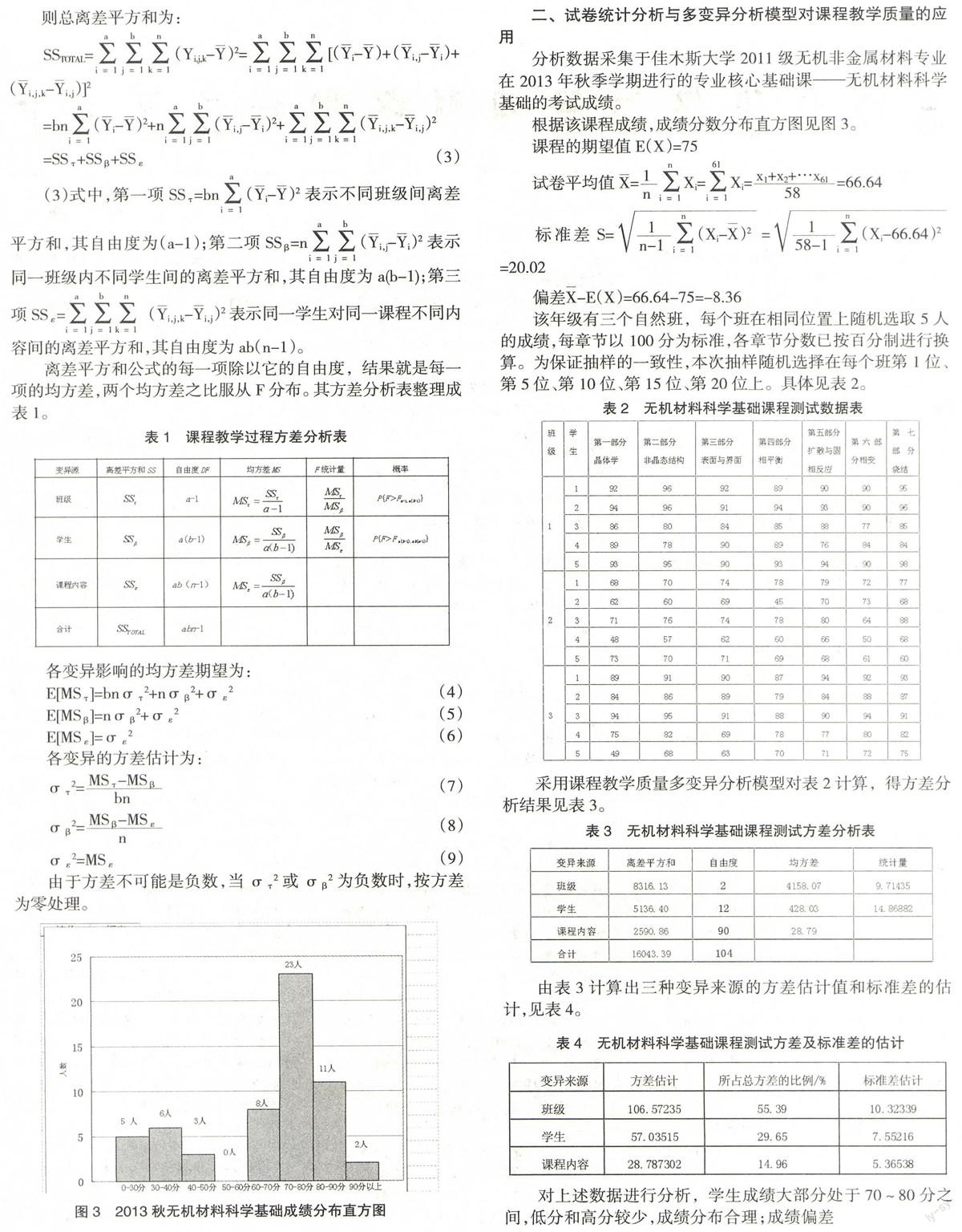
根据该课程成绩，成绩分数分布直方图见图3。

课程的期望值E（X）=75

试卷平均值X= Xi= Xi= =66.64

标准差S= = =20.02

偏差 -E（X）=66.64-75=-8.36

该年级有三个自然班，每个班在相同位置上随机选取5人的成绩，每章节以100分为标准，各章节分数已按百分制进行换算。为保证抽样的一致性，本次抽样随机选择在每个班第1位、第5位、第10位、第15位、第20位上。具体见表2。

采用课程教学质量多变异分析模型对表2计算，得方差分析结果见表3。

由表3计算出三种变异来源的方差估计值和标准差的估计，见表4。

对上述数据进行分析，学生成绩大部分处于70～80分之间，低分和高分较少，成绩分布合理;成绩偏差为负偏差，比预期成绩低，与课程的期望值差距较大，但在合理区间;方差较大，说明学生成绩波动较大，高分与低分相差较多;结合分数分布，还可以发现，成绩大体符合正态分布。

从变异因素看，班级间的变异占55.39%，是主要变异来源;不同学生间的变异占29.65%，是次要变异来源;而同一课程不同内容之间的差异也有一定影响。

针对测试结果，提高无机材料科学基础课程教学质量的首要措施是端正不及格尤其是低于50分的同学的学习态度，培养其良好的学习习惯，消除或减小班级间的差异。根据笔者的教学经验，及专业老师集体讨论的意见，班级的班风要正，学习风气要浓，班级集体观念要强，在专业课程的学习过程中，才会有较好的教学效果。学生间存在变异，说明学生在个人学习态度、学习方法、思维能力等方面存在差异，这是不可避免的。但可以做到以学生为本，因人施教，针对不同学生采用不同的教学方法和手段，尊重个体的需求。至于课程内容间的差异，除了增加辅导答疑频率和时间，强化习题训练外，还应该从完善教师知识结构、提高教师授课水平、灵活教学方法与手段和教学上师生互动等方面入手，全方位提高專业课教学质量，提升学生专业水平，让每个学生都能成才。

三、结语

将多变异分析模型和试卷统计分析方法应用于专业课教学质量评价中，用分析产品生产过程中多个变异来源时质量特征值变异规律的方法去分析专业课教学质量，明确实际教学过程中存在的变异因素和各种变异来源，结合试卷统计分析，为采取有效措施减少总的变异，得出科学的质量数据，为提高教学质量提供依据。

[基金项目：黑龙江省高等教育学会“十二五”高等教育科研课题（课题编号14G133）;佳木斯大学教研课题（项目编号JYLA2012-025）]

参考文献：

[1] 何桢，李国春，石金桥.工序质量分析与控制中的多变异分析方法[J].系统工程理论与实践，2000（5）

[2] 何桢，刘豹，齐二石.基于多变异分析的工序控制方法研究[J].管理工程学报，2002（2）

[3] 彭晓楠.统计过程控制中的多变异分析方法研究[J].制造业自动化，2010（1）

[4] 仲高艳.基于MVA的教学过程质量分析及学习评价方法[J].数学的实践与认识，2011（24）

[5] Montgomery D C .Design and Analysis of Experiment. 4th edition. John Wiley and Sons，1997

[6] 何桢，孔祥芬，宗志宇.多变异分析方法与抽样方案的研究[J].制造技术与机床，2006（11）

[7] 刘宝义，闫慧芝，李蓓，等.血液质量控制过程与多变异分析方法的分析[J].中华医院感染学杂志，2010（13）

[8] 仲高艳.基于MVA的教学过程质量分析方法[M].机械类课程报告论坛论文集.高等教育出版社，2010