利用吉布斯吸附等温式探索求解电解质溶液活度的新方法

韩 梅，刘常青，陈启元，张平民

（中南大学 化学化工学院，湖南 长沙 410083）

溶液活度系数是溶液热力学研究的特性函数，常用于推测溶解度等物理化学性质，对化学化工、生物医药、环境能源以及矿物冶金等方面的研究具有重要的理论指导意义.通过电解质溶液的活度系数可以深化溶液结构理论的认识，有助于相平衡、化学平衡计算及新工艺和新产品开发的研究.

实验测定溶质活度和活度系数的方法主要有电动势和以渗透系数为基础而发展形成的等压法.等压法［1-2］是一种间接测定溶质活度和活度系数的实验方法，采用汽-液体系平衡组成方法，实际测得的是溶剂的活度系数，再通过Gibbs-Duhem方程变换而求算出溶质的活度.这种方法虽然测量范围广，测量精度高，但实验测定繁琐耗时，并且对于不稳定体系难以准确测量.电动势法［3-5］通过测定电池的电势值，根据Nernst方程直接给出溶质的活度系数，测定时间短，测量简单快捷，测定数据的可靠性可与等压法相媲美，但测定限于稀溶液，溶液浓度范围小，不易选择合适的指示电极，有很大的局限性.

对于不稳定体系比如挥发性体系、超高温体系、高浓度不稳定体系等溶液的活度系数尚难以确定.STREY等指出［6］大多数纯正的表面活性剂的活度系数未能确定，这是因为汽液平衡的方法对这类分子不够精确，低温下的活度难以测量，并且其他方法对于低浓度不够敏感.周俊［7］在利用等压法测定铝酸钠溶液体系渗透系数和活度系数的过程中分析了其误差传递规律以及温度和浓度对不稳定性的影响.徐珍等［8］用电导法测定了298.15～343.15K下四丁基氟化铵（TBAF）在DMF中的电导率，采用Debye-Hückel和Osager-Falkenhangen公 式 计 算出TBAF在DMF中的平均活度系数，并讨论了TBAF电解质溶液活度系数的影响因素.在冶金过程中，湿法冶金［9］的氨性体系和火法冶金［10］的高温熔盐中的离子的活度系数都很难测定.陈辉煌等［11］对吉布斯吸附等温式进行了初步探索研究，通过自拟活度系数表达式进行两次拟合计算，得到氯化钴溶液活度系数，结果较为理想.本文作者从电解质溶液表面相和体相的势能入手，在Gibbs吸附等温式的基础上，基于表面势对活度系数的关系，结合Debye-Hückel理论和Pitzer活度系数模型，进行严密推证，提出一种新的实验测量计算模型——表面张力求解活度系数，并进行探索性研究.

1 原理——Gibbs吸附等温式的积分与求解

在表面科学中，Gibbs基于化学热力学原理推导了著名的溶液表面吸附等温式，揭示了定温下溶液表面吸附达到热力学平衡时，溶液表面张力与溶液活度之间的定量关系.Gibbs吸附等温方程式如下［12］：

式（1）中的σ是表面张力，也是表面Gibbs自由能，具有“势”的特质，即表面势.

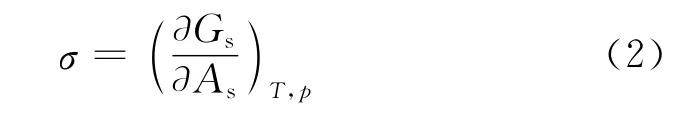
国内曾有学者提出表面势的理论［13］，表面张力σ是属物理学的力学概念的量，单位为N·m-1；表面势σ是属物理化学的热力学概念的量，单位为J·m-2；二者实为同一物理量.

基于Gibbs吸附等温方程式可得此式表明，当温度一定时体系具有下列重要性质：1）吸附量ΓB与溶质的活度aB有关，由于活度与浓度有关，吸附量即与其浓度有关；2）表面张力σ与溶质的活度aB有关，表面张力亦与其浓度有关.

研究人员通常在Gibbs吸附等温方程式的基础上来实验测定吸附量，并定义了正、负吸附的概念.本文作者拟应用表面势的数学表达式探求一种测算电解质溶液活度系数的新方法.表面势σ的数学表达式为Gibbs吸附等温方程式（3）的积分表达式：

式（4）中的K为积分常数；由于ΓB是活度的函数，虽然具体的函数表达式不能确定，但对式（4）中的第二项积分结果一定是与温度和吸附量有关的函数.

当温度T和活度aB一定时，ΓB即为定值，由此可得：

σ＝-ΓBRTlnaB-ΓBRT＋K （5）

根据化学势的一般表达形式类推表面势σ，可将-ΓBRT与积分常数K合并，以σ＊（T，ΓB）表示，则式（4）积分结果可表示为：

σ＝-ΓBRTlnaB＋σ＊（T，ΓB） （6）

式（6）中的σ＊（T，ΓB）应该是aB＝1时溶液的表面势，即表面张力σ；而且σ＊（T，ΓB）还应该满足ΓB→0时趋向于纯溶剂的表面张力.即当aB→0时，溶质的浓度mB→0，没有发生吸附；ΓB→0，意味着溶液的表面张力趋近于纯溶剂的表面张力.因此，若以水为溶剂，则在298.15K时，σ＊（T，ΓB）＝72.14×10-3N·m-1，则式（6）化为：

σ＝-ΓBRTlnaB＋72.14×10-3（7）

2 结果与讨论

2.1 热力学数学模型的建立

电解质溶液的溶质活度aB、平均离子活度系数γ±和平均离子浓度m±三者之间的关系式［14］为：

aB＝（a±）ν＝（γ±m±）ν（8）

式（6）中的溶质活度aB可以用式（8）来代替，即

σ＝-νΓBRTln（γ±m±）＋σ＊（T，ΓB） （9）

由式（9）可知，影响或决定表面势的主要因素是γ±、m±和ΓB.γ±和m±之间存在一定的函数关系，设经验关系式为：

γ±＝f（A，B，C，m±） （10）

式中A、B、C为待定系数，将式（10）代入式（9）可得：

σ＝-νΓBRTln［f（A，B，C，m±）·m±］＋σ＊（T，ΓB） （11）

式（11）即为基于表面势的热力学基本表达式，是本文所述利用表面张力对浓度关系的实验数据求算活度系数的“新方法”的数学表达式，也称新方法的热力学数学模型.新方法基于此模型，利用σ和m±的实验数据，采用最优化拟合的方法求算出待定系数A、B和C，进而可求得活度和活度系数.应用新方法的关键是，首先选定活度系数经验关系的表达式，即选定活度系数函数的具体表达形式；其次选定恰当的吸附量的数学表达式.

2.2 活度系数的经验关系式

在电解质溶液理论中，关于活度系数方面的研究前人有许多成果.从本质上讲，溶液中粒子之间的引力效果使活度降低，粒子之间的斥力效果使活度升高.Debye-Hückel理论［15-16］的活度系数公式体现的是引力效果；Pitzer活度系数模型［17-19］在Debye-Hückel理论基础上考虑了粒子间的排斥力，对“二粒子集团”和“三粒子集团”的相互作用使用维里方程式进行展开，引出了维里系数的概念，体现了斥力效果.

随后KIM［20］对Pitzer电解质溶液求解活度系数的计算公式进行改进，在质量摩尔浓度小于饱和浓度的可测浓度范围内，利用渗透系数法测定的渗透系数计算了304种单电解质水溶液体系的离子相互作用系数，并求得其离子平均活度系数.利用KIM计算法的改进公式可以求解大多数电解质在溶解度范围内的离子平均活度系数，并且相对于Pitzer理论的结果其在高浓度范围与实验值更为接近.

本工作基于Gibbs吸附等温式理论，综合考虑溶液中离子间的引力和斥力效果，应用KIM计算法的改进公式求解电解质溶液的溶质活度系数的形式，进行理论推导计算.

KIM计算电解质溶液活度系数的关系式：

式（12）中，mM（mol/kg）是溶质阳离子M的质量摩尔浓度，其电荷量为zM，化学计量系数为νX；同样，下标X为阴离子；ν＝νM＋νX，I＝1/2∑imiz是离子强度；Aφ、b是Debye-Hückel系数项，BMX和B′MX在KIM理论中用（2-2价型）离子相互作用系数表示，代表第二维力系数的可测量组合，用来解释成对相反电荷离子间的相互作用；CMX为单电解质溶液第三维力系数，用离子相互作用系数CφMX计算，表示三离子间的短程排斥作用力，只有在高浓度溶液中才能起到重要作用，其大小不受溶液离子强度限制.

由于电解质有多种价型，如1-1价型、1-2价型、2-1价型和2-2价型等.对于确定价型的电解质溶液，如CoCl2溶液，属2-1价型，利用KIM法的计算电解质溶液活度系数公式则可变换为：

由此即确定了活度系数的经验关系式.

2.3 吸附量的数学表达式

吸附量ΓB与活度aB之间存在函数关系，但具体的数学表达式很难确定.朗缪尔于1916年提出单分子层吸附理论，其理论模型虽研究表面现象，却并没有受到表面张力概念的影响，而是完全建立在吸附平衡的基础上的［21-22］.前人将其从固体吸附拓展到液体吸附，效果较好.本文作者将朗缪尔吸附应用于新模型的计算.根据溶液表面吸附理论获得溶液表面吸附经验公式为：

为便于最优化计算，对该公式稍作调整，即以mB替代aB，可得：

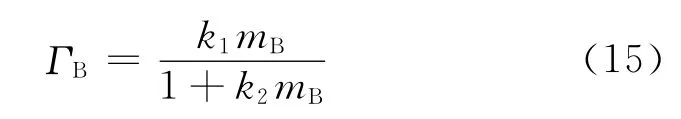
由于吸附量ΓB对表面势σ与ln aB之间的关系影响极大，因此在进行最优化拟合求解待定系数时必须特别注重吸附公式的表达内容，可变换为

式中n可以任取为1、1/2、1/3、1/4和1/5等.需要强调的是，吸附模型有多种，吸附量ΓB也完全可以采用其他的数学表达形式.

2.4 数据处理与分析

对于2-1价型电解质溶液，将式lnγMX的表达式（13）和吸附量ГB的表达式（16）代入热力学数学模型（11）可得：

式（17）是新方法数据处理的具有热力学理论依据的基本公式，或者说是新方法的数学模型，式中k1、k2、A、B和C都为数学模型中的待定系数.

本工作采用最大气泡压力法，在温度298.15 K、常压、离子强度0.57～12.81mol·kg-1的条件下，测定了不同浓度的氯化钴水溶液的表面张力，测试所得数据如表1所示.

表1 不同浓度下氯化钴水溶液表面张力实验数据Table 1 Surface tension of cobalt chloride aqueous solution at different concentrations

根据表1中所列的数据对方程（17）进行了最优化拟合，求算数学模型的待定系数k1、k2、A、B和C（表2），即求得了活度系数经验公式中的待定系数A、B和C.根据求算得到的待定系数值再计算不同浓度的氯化钴溶液的活度系数见表3.按文献中的KIM方法也求算了不同浓度的活度系数，计算结果也一并列于表3中.

表2 方程（17）的待定系数值Table 2 Regression parameters for Eq.17

表3 氯化钴水溶液活度系数文献值与计算值Table 3 Literature data and calculated activity coefficients of cobalt chloride aqueous solution

根据表3中的数据绘制了活度系数对浓度关系的曲线图，如图1和图2所示.在图1中的两条曲线的坐标尺度相同；图2中的两条曲线的坐标尺度不相同.

图1 氯化钴溶液活度系数lnγ±与质量摩尔浓度之间的关系Fig.1 Relational graph of activity coefficients and quality molarity of ions of cobalt chloride aqueous solution

图2 氯化钴溶液不同浓度坐标尺度下的活度系数lnγ±对比图Fig.2 Comparison of the activity coefficients of cobalt chloride solution in different quality molarity scales

从图1可见，曲线下降段为引力效果，由Debye-Hückel理论的活度系数公式表示；上升段为斥力效果，由KIM公式的后半部分表示.对比本工作所获得的数据与KIM法的计算数据：在低浓度范围内偏低，而在高浓度范围内偏高，但整体趋势一致，即随着浓度增大活度系数先下降后上升.在新方法中浓度对活度系数的影响程度较大，或者说新方法的原始数据，即表面张力与浓度之间的关系数据对活度系数数据的显示敏感度较大.当两条曲线采用不同的坐标尺度时（图2），它们有很好的相似性，表明它们对活度系数与浓度关系之间的客观规律具有相同的表达能力，即新方法与KIM法有相同的效能，可以认为用表面张力求解活度系数是可行的.

表4 幂指数n为不同值时求得的待定系数值Table 4 The calculated regression parameters with different exponent n

由上各图可见，当n＝1/2、1/3、1/4或1/5时，相对于KIM法所获得的lnγ±数据而言，本工作所获得的lnγ±数据在全浓度范围内呈现的偏差都比n＝1时的偏差要小.当n取1/4或1/5时所获得的数据比较好，二者的最大偏差值也比较接近.

以上对幂指数n的讨论可以看出，ГB项的修正可以使新模型的计算值的数量级接近文献值.同时说明电解质溶液的吸附不仅仅为单分子层吸附，还应考虑多层吸附等其他吸附形式.此外，新模型采用直接测量求解法，与渗透系数法间接测量有所不同，其上升和下降趋势更为明显，灵敏度相对更高.但有关新模型的研究仍在不断探索中，希望通过对公式改进获得更为精确的活度系数计算公式.

3 结论

1）基于Gibbs吸附等温式，利用数学积分求解，得到表面势的热力学表达式.

图3 不同幂指数下氯化钴溶液活度系数与质量摩尔浓度之间的关系Fig.3 Relational graph of activity coefficients and molarity of ions of cobalt chloride aqueous solution in different exponent

2）新方法的活度系数经验公式是采用KIM渗透系数法计算电解质溶液的溶质活度系数公式的表达形式，将实验测定的表面张力用最优化拟合的数学方法进行拟合，求算经验公式中的待定系数.因此有比较好的理论基础.本工作选取KIM法计算电解质溶液的溶质活度系数公式作为新方法的溶质活度系数经验公式，溶质活度系数经验公式中的待定系数（A、B、C）是依据实验测得的不同浓度下的表面张力数据，采用最优化法拟合计算出来的.因此，新方法同渗透系数法及等压法一样，属于实验测定法.

3）通过分析可知，活度系数曲线在不同坐标尺度下有很好的一致性，这使得通过测定电解质溶液的表面张力计算其活度系数（或活度）成为可能.

此模型计算复杂并且精确度还有待提高，需要进一步进行优化，并将这些理论更好地与实践相结合.对于非电解质溶液以及不稳定体系，现在还缺乏活度系数普遍适合的方法，高温条件下体系性质的工作尚未完全开展，希望可以借助表面张力法得到进一步探究.本工作提出了新的溶液活度计算方法具有一定的理论意义和实用价值.

［1］ROBINSON R A.The activity coefficients of sodium and potassium thiocyanate in aqueous solution at 25°from isopiestic vapor pressure measurements［J］.J Am Chem Soc，1940，62（11）：3131-3132.

［2］陈香，刘士军，黄华强.298.15K时CuSO4-NiSO4-H2O三元溶液体系的活度［J］.湖南师范大学学报：自然版，2014，37（5）：43-48.

［3］卓克垒，王键吉.电动势法在电解质溶液的热力学研究中的应用［J］.化学通报，1995，5（9）：21-27.

［4］王瑞陵，姚燕，吴国梁.电动势法对LiCl-MgCl2-H2O体系热力学性质的研究［J］.物理化学学报，1993，9（3）：357-365.

［5］唐浩，颜永得，张密林.MgCl2在LiCl-KCl熔盐中的电化学特性（英文）［J］.物理化学学报，2013，29（8）：1698-1704.

［6］STREY R，VIISANEN Y，ARATONO M，et al.On the necessity of using activities in the gibbs equation［J］.J Phys Chem B，1999，103（43）：9112-9116.

［7］周俊.渗透系数和活度系数的等压法测定及其在铝酸钠溶液体系中的应用［D］.长沙：中南大学，2003：89-129.

［8］徐珍，吕早生.四丁基氟化铵在DMF中的活度系数测定［J］.化学与生物工程，2014，31（12）：39-41.

［9］朱芝仙.湿法冶金离子溶液中活度的测定、估算及其相互关系［J］.湿法冶金，1985，2（1）：11-17.

［10］邹元燨，周继程，徐元森.冶金熔体热力学的若干研究［J］.金属学报，1982，18（2）：127-140.

［11］陈辉煌，陈启元，刘常青.吉布斯吸附等温式的应用—电解质溶液活度测定新方法［J］.中国有色金属学报，2014，24（7）：1878-1882.

［12］傅献彩，沈文霞，姚天扬.物理化学［M］.北京：高等教育出版，2006：324-329.

［13］彭笑刚.物理化学讲义［M］.北京：高等教育出版社，2012：403-409.

［14］黄子卿.电解质溶液理论导论［M］.北京：科学出版社，1983：1-9.

［15］覃东棉，刘桂华，李小斌.Debye-Hückel理论的研究进展［J］.材料导报，2010，24（13）：107-112.

［16］李以圭，陆九芳.电解质溶液理论［M］.北京：清华大学出版社，2005：57-64.

［17］PITZER K S，MAYORGA.Thermodynamics of electrolytes.II.Activity and osmotic coefficients for strong electrolytes with one or both ions univalent［J］.J Phys Chem，1973，77（19）：2300-2308.

［18］PITZER K S，KIM J J.Thermodynamics of electrolytes.IV.Activity and osmotic coefficients for mixed electrolytes［J］.J Am Chem Soc，1974，96（18）：5701-5707.

［19］PITZER K S，ROY R N，SILVESTER L F.Thermodynamics of electrolytes.7.Sulfuric acid［J］.J Am Chem Soc，1977，99（15）：4930-4936.

［20］KIM H T，FREDERICK W J，Jr.Evaluation of Pitzer ion interaction parameters of aqueous electrolytes at 25℃.1.Single salt parameters［J］.J Chem Eng Data，1988，2（33）：177-184.

［21］解明曙，赵旭，王毅力.颗粒物微界面吸附模型的分形修正——朗格缪尔（Langmuir）、弗伦德利希（Freundlich）和表面络合模型［J］.环境科学学报，2005，25（1）：52-57.

［22］LANGMUIR I.The adsorption of gases on plane surfaces of glass，mica and platinum［J］.J Am Chem Soc，1918，40（9）：1361-1403.