Al-Mg-Zn 三元合金表面张力的估算

周艾琳, 杨志良, 史 航, 李 竹, 吴连得, 吴广新, 张捷宇

(1. 上海大学材料科学与工程学院, 上海200444; 2. 河北工程大学材料科学与工程学院, 河北邯郸056038)

液态金属及合金的表面张力是材料和工程研究中重要的热物性基础数据之一. 表面张力与许多冶金现象或过程都有密切的关系, 如热浸镀、铸造、钎焊、烧结、区域熔炼以及纤维相形成等[1]. 液态金属及合金表面张力的测量方法主要有悬滴法、静滴法、电磁悬浮法和振动液滴法等[2]. 但对于高温下的液态金属, 由于测量表面张力的实验过程难度大、耗时长、花费高,导致许多相关数据缺乏, 因此利用理论模型对液态金属及合金的表面张力进行计算和预测是十分必要的.

国内外研究人员运用理论模型对多元合金体系的表面张力进行了研究. Butler[3]将表面张力与热力学性质联系起来, 所建立的Butler 方程是被广泛运用的计算表面张力的模型之一. Tanaka 等[4]利用计算相图的溶液热力学数据库, 结合Butler 方程计算了二元合金、熔盐以及氧化物的表面张力. Novakovic 等[5]运用Butler 方程计算了Al-Ti 合金的表面张力.Kaptay[6]将Butler 方程应用拓展到晶界上, 研究了体相成分、温度、压力等对晶界偏析现象的影响. Wu等[7]结合Butler 方程、Miedema 模型以及Chou 模型, 研究了Sn 基无Pb 焊料合金二元体系和三元体系的表面张力. Arutyunyan 等[8]利用Butler 方程预测了CaO-Al2O3-CaF2熔渣体系的表面张力. Yan 等[9]运用人工神经网络的方法预测了液态单质金属的表面张力, 并结合热力学数据和CALPHAD 方法计算了液态合金的表面张力. 在此基础上, Yan 等[10]结合几何模型(Kohler 模型、Toop 模型、Chou 模型)与Butler 方程计算了773 K 温度下Sn-Ga-In合金的表面张力, 计算值与实验值基本一致. Prasad 等[11-12]结合新几何模型计算了Al-Sn-Zn三元液态合金的表面张力, 并研究了体相和表相间的关系. 可见, 通过将Butler 方程和几何模型相结合, 计算得到的多元液态合金表面张力结果更为准确, 因此本工作也利用该方法计算Al-Mg-Zn 液态合金的表面张力.

Al-Mg-Zn 合金具有易于铸造、加工、高强度、高耐腐蚀性和成本低等优点. 热镀铝锌合金镀层因其较好的耐腐蚀性能越来越受到人们的重视, 其中作为高耐腐蚀合金镀层的Zn-6%Al-3%Mg (ZAM)被广泛应用于桥梁、公路、农业等领域[13]. 此外, Zn-0.2%Al-0.5%Mg合金镀层在大气腐蚀环境中, 表现出了良好的抗蚀效果[14]. Zn-4.5%Al-0.1%Mg 合金镀层组织性能与Galfan(锌-5%铝-稀土合金镀层)相近, 有良好的可焊性和耐腐蚀性.

本工作结合Butler 方程和Chou 模型, 计算了973 K 温度下, Al-Zn, Mg-Zn, Al-Zn 二元合金的表面张力, 并在此基础上计算了Al-Mg-Zn 三元合金的表面张力, 为进一步研究界面反应、热浸镀、铸造、凝固等提供数据支持.

1 表面张力计算模型

1.1 Butler 方程

1932 年, Butler[3]提出将多组分溶液的表面相和体相看成是两个独立的物相. 平衡的溶液A 有一个紧密相连的表相, 在两相间划分出不同区域的表相S, 两边都包含均匀相. 假设溶液表相内的组分与体相内的组分在热力学上达到平衡, 则表面张力与热力学性质可以用如下公式表示:

式中: σij为溶液的表面张力, σi和σj分别为纯组分i 和j 的表面张力; T 为温度, 单位为K; R 为摩尔气体常数; 上标S 和B 分别代表表相和体相; XSi, XSj和XBi, XBj分别表示组

式中: N0为阿伏伽德罗常数; Vi为纯物质i 的摩尔体积; 若为密堆积, 则L=1.091.

式中: βi, βj为经验参数, 其数值与熔体的特性有关. 对于合金体系, βi或βj取决于表相和体相中的配位数ZS/ZB. 通常βi或βj的取值范围为0.75～0.83, 适用于熔融金属及其过冷合金亚稳态的表面张力计算.

1.2 新几何模型

Chou[16]提出了通过二元合金的性质来推算三元系乃至多元系合金性质的新一代几何模型. 新模型克服了传统模型在理论上存在的缺陷, 比传统模型有着更好的精度.

在三元系中, 三元系的过剩表面张力为

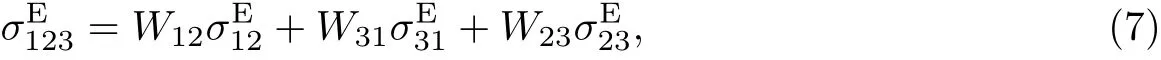
式中: σE123和σEij分别为三元系和二元系的过剩表面张力, 且

Wk为权重因子, 可表示为

其中xk代表三元系组分的摩尔分数, Xi(ij)代表二元系ij 中i 组元的摩尔分数. Xi(ij)的计算公式如下:

式中, ξij为相似系数, 可定义为

其中ηk为偏离函数,

三元系的表面张力与理想熔体的表面张力及三元系的过剩表面张力的关系为

2 计算结果与讨论

二元系的过剩吉布斯自由能函数用Redlich-Kister(R-K)多项式[17]表示, 即

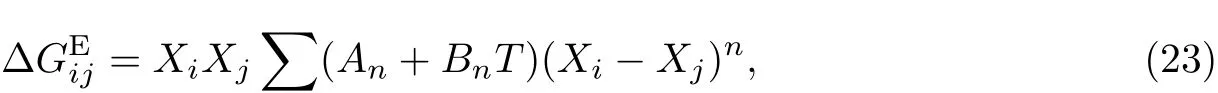
式中: Xi,Xj为二元系中组元ij 的摩尔分数; GEij为二元系过剩吉布斯自由能; An, Bn为待定参数, 可由热力学和CALPHAD 方法求得. Al-Mg, Al-Zn 和Mg-Zn 二元合金的过剩吉布斯自由能函数如表1 所示.

表1 Al-Mg, Al-Zn 和Mg-Zn 二元合金的过剩吉布斯自由能函数Table 1 Excess Gibbs energy of the Al-Mg, Mg-Zn and Al-Zn binary alloys

Al, Mg 和Zn 元素的相关物理化学参数如表2 所示. 因为所计算的体系为液态合金, 所以在利用Butler 方程计算时, L=1.091, β =0.75.

表2 Al, Mg 和Zn 元素的质子量, 密度和表面张力参数Table 2 Data of atomic mass, density and surface tension of pure metal

2.1 Al-Mg, Al-Zn 和Mg-Zn 二元合金的表面张力计算

图1 是973 K 温度下, Al-Mg, Al-Zn 和Mg-Zn 二元合金的表面张力曲线, 反映了3 种合金表面张力随组元成分的变化规律. 从图1(a)和(b)可以看出, 在Al 熔体中加入金属Mg 和Zn, 随着金属Mg 或Zn 摩尔分数的增加, Al-Mg 和Al-Zn 二元合金的表面张力呈减小趋势.从图1(c)可以看出, 在Al 熔体中逐渐加入金属Mg, 会降低合金的表面张力.

Al-Mg 和Al-Zn 二元合金表面张力的实验数据在文献[20]中均有报道, 而Mg-Zn 的实验数据没有找到, 所以本工作对Al-Mg 和Al-Zn 两个体系进行了误差对比. Al-Mg和Al-Zn 二元合金表面张力的计算值与实验值的误差对比如表3 和4 所示, 误差范围分别为0.09%～0.72%和0.06%～2.79%. 计算结果与文献中的实验数据吻合良好, 反映了表面张力随成分变化的规律.

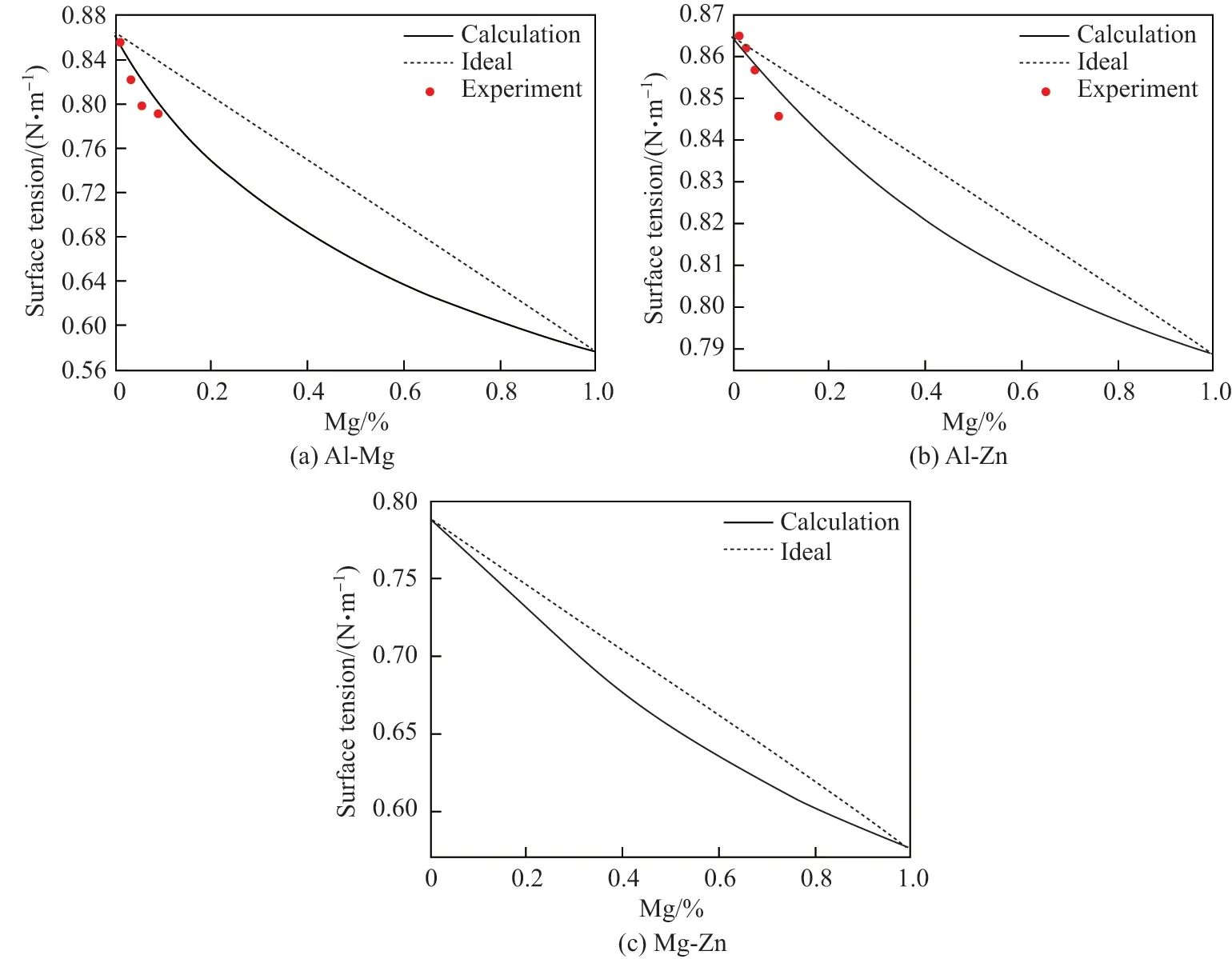
图1 973 K 温度下, Al-Mg, Al-Zn, Mg-Zn 二元合金的表面张力Fig.1 Surface tensions of the Al-Mg, Al-Zn, Mg-Zn binary alloys at 973 K

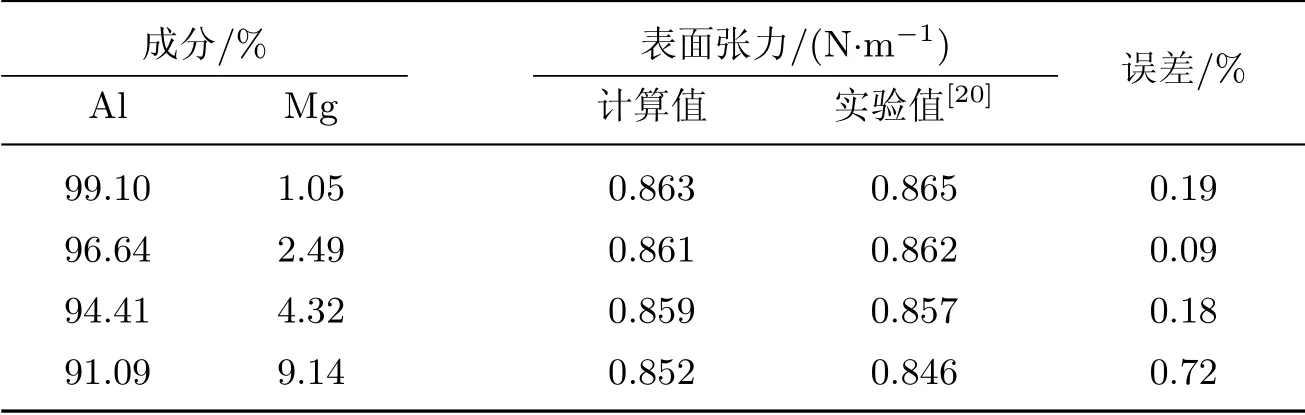
表3 Al-Mg 二元合金表面张力计算值与实验值的误差对比Table 3 Comparisons of the surface tensions of the Al-Mg binary alloy between calculated and experimental data

表4 Al-Zn 二元合金表面张力计算值与实验值的误差对比Table 4 Comparisons of the surface tensions of the Al-Zn binary alloy between calculated and experimental data

2.2 Al-Mg, Al-Zn 和Mg-Zn 二元合金的过剩表面张力计算

Al-Mg, Al-Zn 和Mg-Zn 二元合金的过剩吉布斯自由能计算结果如图2(a)所示. 可以看出, Al-Mg 和Mg-Zn 二元合金的过剩吉布斯自由能相似, 对于理想溶液都发生负偏差而Al-Zn二元合金的过剩吉布斯自由能对于理想溶液是正偏差. 过剩表面张力是表示溶液表面张力对于理想溶液的实际偏差. 从图2(b) 中可以看出, Al-Mg, Al-Zn 和Mg-Zn 二元合金的过剩表面张力均为负值, 即这3 个二元合金对于理想溶液均为负偏差. 在Al 熔体中加入Mg 和Zn, 在Zn 熔体中加入Mg, 都会降低二元合金的表面张力, 所以Mg 和Zn 是表面活性物质.

图2 973 K 温度下, 二元合金过剩吉布斯自由能及过剩表面张力Fig.2 Excess Gibbs energy and excess surface tensions of the binary alloys at 973 K

2.3 Al-Mg-Zn 三元合金的表面张力计算

针对文献[20]中报道的实验值, 特别进行了点对点的计算, 计算值与实验值的误差对比如表5 所示, 误差范围在2.92%～4.98%, 计算结果与文献中的实验数据吻合.

表5 Al-Mg-Zn 三元合金表面张力计算值与实验值的误差对比Table 5 Comparisons of the surface tensions of the Al-Mg-Zn ternary alloy between calculated and experimental data

图3 反映了表面张力随成分的变化趋势, 所得出的计算值与实验值的变化规律一致. 可见, 运用Chou 模型对三元合金的表面张力进行计算是可行的. 下面, 将这一方法推广运用到对Al-Mg-Zn 三元合金的全浓度范围的计算.

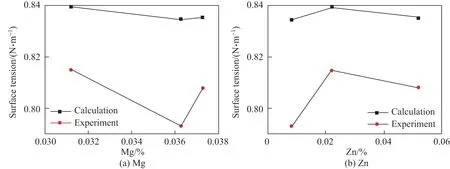
图3 Al-Mg-Zn 三元合金表面张力计算值与实验值对比Fig.3 Comparisons of the surface tensions of the Al-Mg-Zn ternary alloy between calculated and experimental data

在研究三元系中某一组元对整个体系的作用时, 可以固定另外两个组元的成分比例, 从而研究该组元成分的变化对三元系表面张力的影响, 即三元系过一元素点的垂直截面. 本工作中所计算的成分比例如表6 所示.

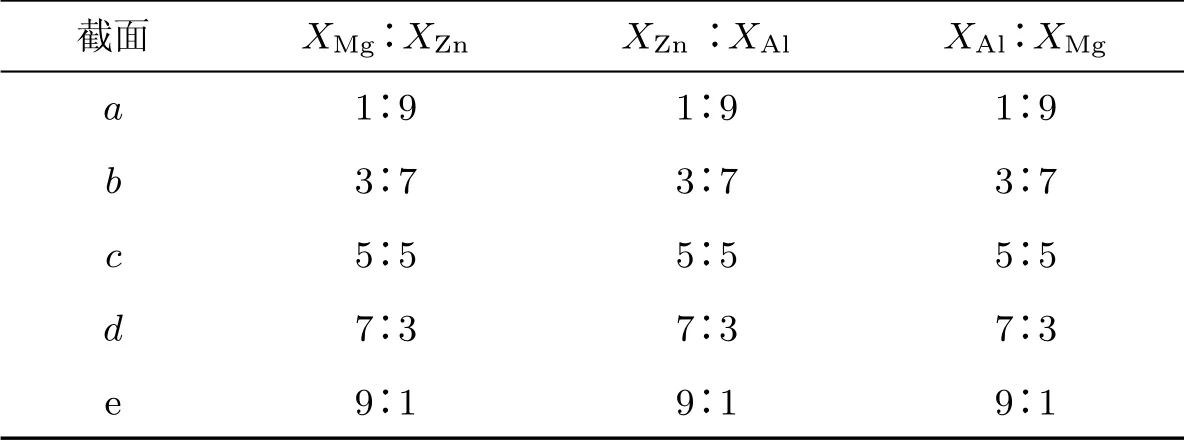
表6 Al-Mg-Zn三元合金各截面成分比例Table 6 Cross section in the Al-Mg-Zn ternary alloy

Al-Mg-Zn 三元合金表面张力与各组元成分之间的关系如图4 所示. 可以看出, Al-Mg-Zn三元合金表面张力基本处于0.575～0.864 N/m 之间, 并且随着Mg 含量的增加, 表面张力呈减小的趋势. 对于图4(c)中曲线e, 即成分比例在XAl∶XMg=9∶1 时, 随着Zn 含量的增加,Al-Mg-Zn 三元合金表面张力呈先增大后减小的趋势. Al-Mg-Zn 三元合金表面张力随着各组元成分的变化大致呈现单调增加或者减小的趋势.

图4 Al-Mg-Zn 三元合金在973 K 的表面张力Fig.4 Surface tensions of the Al-Mg-Zn ternary alloy at 973 K

将各表面张力曲线外延可得到该曲线与纵坐标的交点. 这些交点分别对应着Al-Mg-Zn三元系合金特殊成分点的表面张力值. 当该组元的成分趋近于0 时, Al-Mg-Zn 三元系转变为不含该组元的二元系, 其表面张力由另外两个组元构成的二元系表面张力决定. 当组元的成分趋近于1 时, Al-Mg-Zn 三元系转变为仅含该组元的纯物质, 其表面张力值就是该纯组元的表面张力.

2.4 Al-Mg-Zn 三元合金的过剩表面张力计算

Al-Mg-Zn 三元合金的过剩吉布斯自由能与过剩表面张力随成分的变化如图5 所示. 可以看出, 在Al 熔体中加入Mg 或Zn, 过剩吉布斯自由能和过剩表面张力对于理想溶液是负偏差.

对比图5(a)和(b)可以看出, 随着金属Mg 含量的增加, 过剩吉布斯自由能和过剩表面张力变化规律相同, 都是先降低后增大. 对比图5(c)和(d)可以看出, 随着Zn 含量的增加, 过剩吉布斯自由能先降低后增大, 而过剩表面张力则不断降低. 图5(d)中的a 曲线, 即成分比例为XAl∶XMg=1∶9 时, 随着Zn 含量的增加, 过剩表面张力先降低后增大, 与其他成分不同; 而b曲线, 即成分比例为XAl∶XMg=3∶7 时, 曲线的变化规律与其他成分也略有不同, 此类现象有待后续工作的研究.

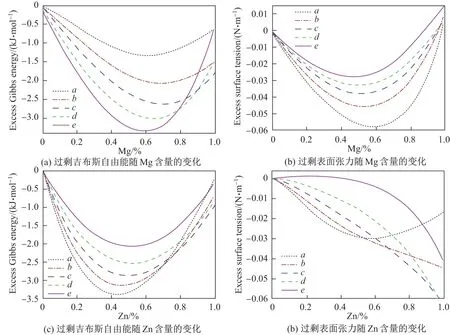
图5 973 K 温度下, Al-Mg-Zn 三元合金过剩吉布斯自由能及过剩表面张力Fig.5 Excess Gibbs energy and excess surface tensions of the Al-Mg-Zn ternary alloy at 973 K

3 结 论

(1) 在973 K 温度下, 利用Butler 方程计算的二元合金表面张力与实验值对比, 误差范围在0.06%～2.79%. 在Al 熔体中加入Mg 或Zn, 都会降低该熔体的表面张力.

(2) 在973 K 温度下, 结合Butler 方程和Chou 模型计算的三元合金表面张力与实验值对比, 误差范围在2.92%～4.98%. Al-Mg-Zn 三元合金表面张力的计算值范围为0.575～0.864 N/m, 并且随着Mg 含量的增加, 表面张力呈减小的趋势; 随着Zn 含量的增加, 表面张力逐渐增加.