破片质量对钨合金破片侵彻威力的影响

赵小峰

(海军装备部,西安 710065)

随着作战飞机与各种精确制导弹药的飞速发展，防空反导技术的研究已迫在眉睫[1-3]。防空反导战斗部所使用的毁伤元主要有多爆炸成型弹丸(MEFP)、多线性爆炸成型弹丸(MLEFP)及破片等。目前应用最为广泛的毁伤元为预制破片，其主要特点为：良好的成形性和加工优势；单枚破片质量及形状可控；飞散角以及空间分布可控。其中，预制破片以钨合金破片应用为主，其特点为密度高、存速能力好、对目标的穿透性强、对战斗部空间体积利用率高[4-6]。

目前对破片的研究多集中于破片形状对破片存速能力的影响、装药结构对破片分布的影响等方面。经研究，立方形破片具有集束优、威力大和空气阻力小、可形成较高的破片存速的特点，因此已被广泛应用于当前杀伤型战斗部中，因此研究立方体破片对靶板侵彻威力的影响具有重要意义[7-8]。现有立方体破片对靶板侵彻威力的研究虽研究了质量对破片威力的影响，但没有研究不同破片质量对其极限穿深的影响。

通过理论计算、数值仿真及试验等方法，对不同质量的立方体钨合金破片的极限穿深能力进行了研究。具体方法为不同质量立方体破片战斗部装填比相同，及保证破片初速相同，对比理论计算、数值仿真以及试验的结果，确定不同质量立方体钨合金破片的极限穿深，为立方体钨合金破片战斗部的设计提供指导。

1 理论计算

1.1 模型的建立

为了探讨单枚破片质量对破片侵彻能力的影响，应尽量减少其他参数对破片侵彻威力的影响因素，因此在进行设计时，破片均选用立方体结构，战斗部装填比相同为0.7，威力半径相同为10 m。

破片参数如表1所示。战斗部模型如图1所示。

表1 破片参数

图1 破片战斗部模型

战斗部由起爆装置、端盖、破片和主装药组成，破片布于内衬上，由于内衬材料为2A12铝且厚度为1 mm，因此可以忽略内衬对破片的影响，即可视破片布于主装药上。

1.2 破片初速计算

对于周向破片的平均初速的计算，一般采用格尼公式计算：

(1)

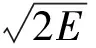
本文所使用主装药的格尼系数为2 780，根据式(1)可知，炸药指定时，破片初速只与装填比有关，因此表1中三种破片初速相同，将装填比代入式(1)中进行计算可得，三种破片的平均初速均为2 000 m/s。

1.3 破片侵彻威力计算

破片侵彻威力半径为10 m，根据速度衰减计算公式：

vx=v0e-αx

(2)

(3)

式中：α为破片速度衰减系数；A为修正系数，取A=1.12；CD为破片迎面阻力系数；ρa为当地空气密度；S为破片迎风面积；mf为破片质量。

根据计算，三种破片在10 m处的剩余速度见表2。

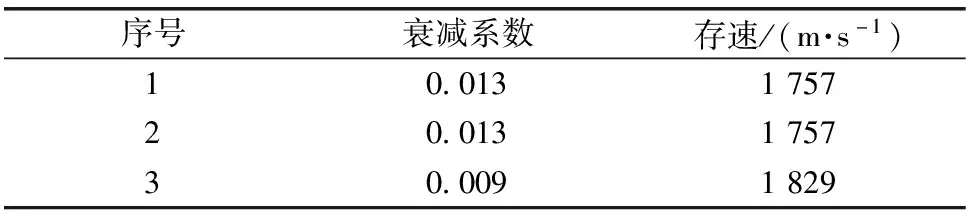
表2 破片剩余速度

对破片侵彻靶板威力计算公式常用THOR方程进行计算：

hmax=1.638 706×10-5-c11/c12S-1(15 432.1m)-c13/c12×

(secθ)-c14/c12(3.280 84vx)(1-c15)/c12

(4)

式(4)中：hmax为破片能够穿透的靶板最大厚度；S为破片碰撞面积即迎风面积；m为破片初始质量；θ为破片弹道与靶板法线的夹角(默认垂直于靶板)；c11、c12、c13、c14、c15为每种靶板材料分别定义的系数。

根据式(4)进行计算，三种不同破片侵彻威力的理论计算结果如表3所示。

表3 破片对靶板侵彻深度

2 数值仿真

2.1 模型的建立

由于战斗部模型比较大，对其进行仿真计算时用时较长，因此简化模型，以理论计算破片在10 m处的存速为数值仿真破片的侵彻初始速度，采用AUTODYN软件进行仿真，建立模型如图2所示。

模型中网格大小为1 mm，选用材料靶板为Q235钢，破片为钨合金，参数选用AUTODYN软件自带材料参数。为靶板添加边界条件：沿破片速度方向速度为恒定值0；为破片添加初始条件：初速沿垂直于靶板上表面方向，大小为表2中存速。

图2 侵彻模型

2.2 仿真结果

判断破片对靶板侵彻深度不再增加的判断依据为破片速度发生反向的现象，本研究中破片侵彻靶板过程中破片的速度变化如图3所示。

图3 不同质量破片侵彻靶板时速度变化

由图3可以看出，在10 m处破片尺寸越大，剩余速度越大。随着侵彻深度的增大，三种破片速度均逐渐减小，在某时刻速度变为0后速度发生反向，此时侵彻结束。

不同质量破片对靶板侵彻的仿真结果如图4所示。

图4 不同质量破片对靶板侵彻结果

由图4可以看出，钨合金破片在侵彻靶板过程中会发生变形，同时随之破片质量的增大，立方体钨合金破片对靶板的侵彻深度逐渐增大，侵彻深度见表4。

表4 破片对靶板侵彻深度

由表3、表4可以看出，不同质量钨合金立方体破片对靶板的侵彻，数值仿真结果与理论计算结果存在误差，且质量越大误差越小。

2.3 破片侵彻威力计算公式修正

利用数值仿真计算结果对破片侵彻威力计算公式进行修正，修正形式如下：

hmax=1.638 706×10-5-c11/c12S-1(15 432.1m)-c13/c12×

(secθ)-c14/c12(3.280 84vx)(1-c15)/c12-(am2+bm)

(5)

将数值仿真计算结果代入式(5)中，得到破片侵彻威力修正公式如下：

hmax=1.638 706×10-5-c11/c12S-1(15 432.1m)-c13/c12×

(secθ)-c14/c12(3.280 84vx)(1-c15)/c12-

(-0.076m2+2.3m)

(6)

由于仿真结果小于理论计算结果，因此式(6)中-0.076m2+2.3m≥0，因此式(6)适用范围为0≤m≤30.4 g。

验证破片侵彻威力修正公式的正确性，应进行静爆试验进行验证。

3 实验研究

将战斗部竖直置于平台上(图5)，Q235靶板竖直放置在距战斗部10 m处，靶板厚度从左到右依次为12、14、16、22、24、26 mm。

试验用战斗部共三发，装填比均为0.7，三发战斗部所用破片与表1对应。试验测得三发战斗部破片对不同厚度靶板穿透效果如图6所示，穿透率如表5所示，柱形图如图7所示。

图5 静爆试验布局

图6 不同质量破片对不同厚度靶板的侵彻结果

图7 不同质量破片对不同厚度靶板的穿透率

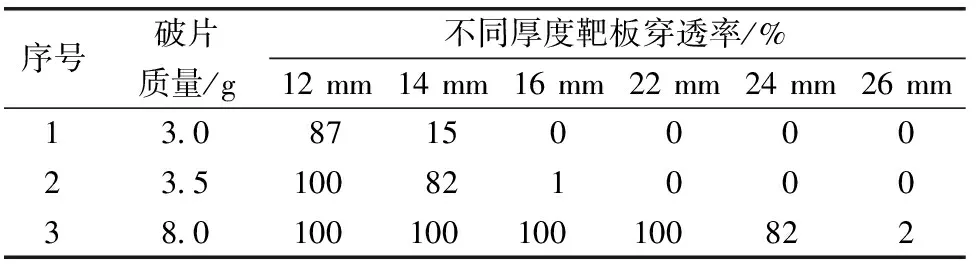
表5 威力半径10 m处破片对靶板侵彻结果

每种破片最大侵彻深度以靶板穿透率50%为判断依据，即靶板穿透率为50%时，判定为破片最大侵彻深度。

对表5进行线性插值求取不同质量破片穿透率为50%时靶板的厚度，公式如下：

(7)

式(7)中：a为破片穿透率小于50%时最小靶板厚度；b为破片穿透率大于50%时最大靶板厚度；c为破片穿透率小于50%时最小靶板厚度的穿透率；d为破片穿透率大于50%时最大靶板厚度的穿透率。

根据式(7)计算得到静爆试验破片最大侵彻深度如表6所示。

表6 威力半径10 m处破片最大侵彻深度

由表6可以看出，3.0 g破片最大侵彻深度试验值为13 mm，与修正公式计算结果误差为0.8%；3.5 g破片最大侵彻深度试验值为14.8 mm，与修正公式计算结果误差为3.5%；8.0 g破片最大侵彻深度试验值为24.8 mm，与修正公式计算结果误差为2%。

将理论计算结果、修正公式计算结果、试验结果进行对比分析，破片最大侵彻深度hmax随质量变化曲线如图8所示。

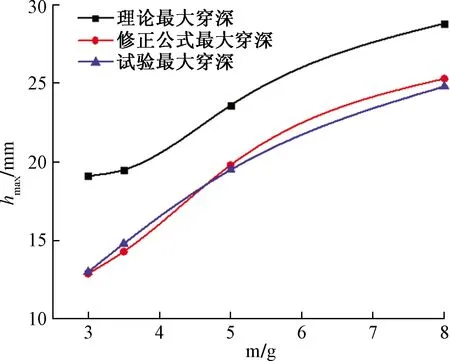
图8 破片最大穿深随质量变化曲线

由图8可以看出，随着破片质量的增大，破片最大侵彻深度逐渐增加，但增大率逐渐变缓，说明破片质量在一定范围内增大有利于提高破片最大穿深，当增大到一定值时，破片最大穿深不再明显增加；同时，试验结果与修正公式计算结果及数值方真结果基本一致，误差小于3.5%。

4 结论

研究破片质量与最大穿深关系的条件是，破片均为立方体破片，战斗部装填比相同且为0.7，威力半径为10 m。

随着破片质量的增大，破片最大侵彻深度逐渐增加，但增大率减小，试验结果表明，破片最大侵彻深度随破片质量的增大，与理论计算结果的误差越小。

对破片最大侵彻深度理论计算公式进行了修正，修正后计算结果与实验结果误差小于3.5%。