公理化局部有限空间中映射连续性的扩展＊

韩相彦

（韩国全北国立大学数学理论与应用研究所数学系，韩国全州 561-756）

公理化局部有限空间中映射连续性的扩展＊

韩相彦

（韩国全北国立大学数学理论与应用研究所数学系，韩国全州 561-756）

用公理化方法研究了局部有限空间中的连续映射及其扩张问题。给出了局部有限空间的公理化定义方法；利用邻近关系研究了局部有限空间中的连续映射、同胚和局部同胚等问题；通过对局部有限空间变形的研究，定义了局部有限空间的一种特殊收缩核，有效地解决了局部有限空间中连续映射的扩张问题。

局部有限空间；ALF空间；最小开邻域；边界；邻近关系；同胚；局部同胚；组合同胚；抽象胞腔复形；扩张问题；收缩核

在应用拓扑理论中（如数字拓扑学），连续映射的扩张问题是一个非常重要的研究对象。映射的扩张一般定义如下：对于一个映射f：X→Y，称映射F：X′→Y是f的扩张，如果f是F在X⊂X′上的限制，即F′|X＝f。本文将用公理化方法研究局部有限空间中的连续映射及其扩张问题。

Alexandroff空间［1］可以直接推广到多值情形下（不同于模糊，译者注），如局部有限空间（LFS）等。在计算机中，LFS可被清晰地表达出来，帮助人们利用计算机进行拓扑的探索、实验和计算。在现代数学中，LFS是一个大家熟知的非常宽泛的概念，它的每个元素可用一些几何图形来描述，如三角形、矩形、平行四边形、梯形等（见图1）。而Khalimsky空间可以视为LFS空间的特例。

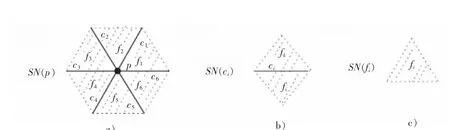
图1 ALF空间中元素p，ci和fi的最小邻域，i∈｛1，2，3，4，5，6｝，k＝i（mod6）＋1［11］Fig.1 Smallest neghbourhoods of elements p，ciand fiof an ALF space，i＝｛1，2，3，4，5，6｝and k＝i（mod6）＋1［11］

另一方面，从应用的角度来说，LFS太宽泛，因此KOVALEVSKY［2－3］建议给出LFS理论的公理化研究方法。称满足相应公理的LFS为公理化的局部有限空间（简称ALF空间）。在ALF空间中，所有元素的邻域关系具有自反性、反对称性和传递性。基于邻域关系的这些性质，每个ALF空间的子空间的边界具有如下特征：所有边界都比较稀疏，边界F的边界仍然是F。这些特征在应用中显得非常重要。

现已有若干关于ALF空间的研究［2，4－5］，然而对于ALF空间之间连续映射的研究还相对较少。因此，本文在文献［4］、文献［2］和文献［5］研究的基础上，将提出自己独特的研究内容。本文所要研究的ALF空间之间连续映射的扩张问题对于ALF空间本身的研究也是非常有帮助的。设X，Y是2个ALF空间，F：X→Y是一个映射，称F：X→Y保持邻域关系，如果y∈SN（x，X）蕴含F（y）∈SN（F（x），Y），其中SN（x，X）（相应地，SN（F（x），Y））表示x（相应地，F（x））的最小邻域（参见公理1和公理2）。由于ALF空间是利用邻域定义的（定义9），所以可以利用保持邻域关系的映射来表现连续映射和同胚。对ALF空间的变形，还可以讨论其收缩核（定义14）。另外，受文献［4，6-7］中对于连续映射扩张问题研究的启发，还可以利用收缩核来处理ALF空间之间连续映射的扩张问题。

本文中，第2节，主要列举关于ALF空间的一些基本概念和基本性质；第3节，讨论ALF空间之间连续映射和同态的性质；第4节，引入ALF空间收缩核的概念并且结合同态讨论相应性质，还将通过收缩核来处理连续映射的扩张问题；第5节，作一总结，并且对于ALF空间连续映射扩张问题的应用进行讨论。

2 ALF空间的一些性质

文献［5］给出了局部有限空间的各公理的合理解释，为了本文的自封性，将在这里重复一些定义和例子。需要指出的是，前面的公理体系中涉及到的一类特殊的最小邻域，不一定是经典点集拓扑中的邻域。

用公理化方法定义的邻域［5］实际上是所谓的邻域空间［8］的特征的一个抽象，然而在现代拓扑理论中，“邻域”是一个在拓扑空间之后定义的概念。本文中所考虑的邻域空间（或仅称为空间）是指一个序对S＝（E，U），其中E是一个非空集合，U是E的一个子集族，它们满足：E的每一个元素都含在U的一些成员中（U中含有e∈E的成员称为e的邻域）。一个空间称为局部有限的，如果E的每一个元素只有有限个邻域。接下来，将考虑一种特殊的邻域空间，称为ALF空间，它满足下面的公理1—公理4。

公理1 空间中的每一个元素的邻域系对有限交封闭（不含空交），即如果A，B∈U且e∈A∩B，则A∩B∈U。

需要注意的是，本文中的邻域在概念上并不是点集拓扑学中的邻域，其性质将被逐步展开讨论。由于空间是局部有限的，每一点e都存在最小邻域（即所有邻域的交），记作SN（e）。从而每一个邻域都包含它的最小邻域。在后面的内容中，将证明ALF空间的最小邻域都是经典意义下的开集（见推论1）。

公理2 空间中必然有些元素拥有多于一个的邻域。

图1给出了ALF空间作为抽象胞腔复形的最小邻域的例子［2－3］，元素e∈E的最小邻域及其势依赖于e的类型。图1a）中的点p的最小邻域SN（p）＝｛p，fi，ci|i∈［1，6］Z｝具有13个元素；图1b）中点ci的最小邻域有3个元素，而其他点的最小邻域则只有2个元素；图1c）中每个点fi的最小邻域都是单点集。

为了建立公理3和公理4，需要利用以下基本概念。

定义1［2］如果b∈SN（a）蕴含a∈SN（b），则称a和b是相伴的。

从上述定义可以看出，相伴关系是对称的。又因为a∈SN（a），所以相伴关系是自反的。相伴关系的定义和文献［9］中邻接关系的定义非常相似（多维的情形可以参见文献［10］、文献［11］和文献［12］），但是它们又显然不同，因为相伴关系并不要求相伴元素的个数相同。

对于ALF空间S以及e∈S，假设与e相伴的元素个数不超过某个固定的自然数。这一假设是非常重要的，原因有如下2点。第一，它保证了ALF空间中极大元素的存在性。这里，称e是极大元，如果它的最小邻域是单点集（可与文献［2］和文献［3］中的引理MM比较）；第二，它还保证了极小元素的存在性。这里，称e是极小元，如果它除自身外不包含于任何最小邻域。这也说明了一个ALF空间的维数是有限的。

定义2［5］设S＝（E，U）是一个LF空间，A⊆E。如果序列（a1，a2，…，ak），ai∈A（i：1，2，…，k）满足：对任意的果i≠j，ai和aj相伴，则称A是a1到ak的相伴路径。

定义3［2］集合A⊆E被称为是连通的，如果对任意的a，b∈A，存在相伴路径B⊆A，且a，b∈B。

文献［3］（第34页）中指出，对于一个ALF空间，基于相伴关系定义的连通性等价于拓扑连通性。

文献［2］和文献［3］中对于拓扑空间的边界定义如下。

定义4 设S＝（E，T）是一个拓扑空间，A是E的非空子集。令

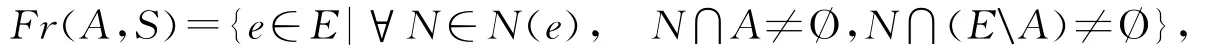
则称Fr（A，S）是A在S中的边界，其中N（e）表示e在拓扑空间S＝（E，T）中的邻域系。

从定义4可以看出，e的每一个邻域都包含一个含有e的开集。在ALF空间情形下，鉴于公理1的要求，我们定义边界时要求这个开子集是包含e的最小邻域。

接下来的2个公理都与边界有关。

KOVALEVSKY［2－3］假设ALF空间中的最小邻域都是经典拓扑意义下开集，并把定义4应用到邻域空间中，这一点将在下面被考虑。

定义5［5］设S＝（E，U）是一个ALF空间，SN：E→2E是最小邻域映射。定义二元关系N为（a，b）∈N当且仅当a∈SN（b），称N是S＝（E，U）的邻域关系。

定义6［2］任意a，b∈Fr（A，S），其中A⊆E，称元素a和b相互对立，若a∈SN（b），b∈SN（a），且其中一个元素属于A，另一个属于E＼A。

定义7［2］A的边界Fr（A，S）称为稠密的，若Fr（A，S）至少包含1组相互对立的元素，否则Fr（A，S）称为稀疏的。

考虑在边界上存在相互对立的元素的情形，“稠密”的意思是指在边界上有2个子集互相“平行”（共用一部分边界）。

公理3 E的任意子集A的边界Fr（A，S）都是稀疏的。

由定义4可知，A和E＼A有相同的边界。

定理1［2－3］局部有限空间S满足定理3当且仅当S的邻域关系N是反对称的。

关于边界还有另一个重要性质：A的边界F＝Fr（A，S）与Fr（F，S）的边界相同。文献［9］和文献［10］证明了，只有当邻域关系不具有传递性时，Fr（A，S）与F＝Fr（A，S）才不相同，这一事实在证明满足以上公理的最小邻域都是开集中将起到重要作用。

公理4 Fr（A，S）的边界与Fr（A，S）相等，即Fr（Fr（A，S），S）＝Fr（A，S）。

为了构造ALF空间的拓扑结构，文献［2］和文献［3］引入了ALF空间的开集和闭集的概念，并用邻域空间做了等价刻画（对比文献［8］第24页）。

定义8［2］设S＝（E，U）是一个ALF空间，O，C⊆E。称O为S中的开集，若O中不含Fr（O，S）中的点；称C为S中的闭集，若Fr（O，S）⊆O。

引理1［2］设S＝（E，U）是一个ALF空间，SN：E→2E为最小邻域映射且A⊂E，根据定义8，A为S中的开集当且仅当∀e∈A有SN（e）⊂A。

由公理1、定义4和定义8，可以证明以下定理，即ALF空间中的开集满足一般拓扑的3条公理。

定理2［2－3］每个ALF空间S的开子集族形成S上的一个拓扑。

推论1［2－3］设S＝（E，U）是一个ALF空间，e∈E。则e的最小邻域既是定义8意义下的开集，也是通常的拓扑意义下的开集，并且它是包含e的最小开子集。

相应的证明可以参照文献［2］和文献［3］。

从推论1可以看出，对于一个ALF空间，它的所有元素的最小开邻域构成了其对应的拓扑空间的一个基，ALF空间的子集的性质可以由这些最小邻域族来表达。下面给出ALF空间的具体定义。

定义9［5］设E是一个集合，N是E上的一个二元关系，序对S＝（E，N）被称为是一个公理化的局部有限空间，如果S满足公理1—公理4。特别的，二元关系确定了每个元素的最小邻域SN（e）＝｛x：（x，e）∈N｝。

ALF空间就是一类可以完全由其最小邻域族确定的特殊的拓扑空间。文献［3］中还证明了每个ALF空间是Alexandrov空间（也可参见文献［13］），从而对于ALF空间理论的研究可以作为对Alexandrov空间理论研究的一部分。

3 ALF空间的连续映射

连续映射是一般拓扑学中的重要概念之一。设X和Y是拓扑空间，f：X→Y为映射，x∈X，如果对f（X）的任意开邻域Of（x）⊆Y，存在x的开邻域Ox⊆X使得f（Ox）⊆Of（x），则称f在点x连续。换言之，对f（x）的任意开邻域Of（x）⊆Y，Of（x）在映射f下的原像是x的开邻域。然而，ALF空间的连续映射必须将X中任一点x的最小邻域映射到F（x）的最小邻域中（见定义10）。由于ALF空间中的邻域有不同于Hausdorff空间的性质，因此，ALF空间的连续映射对于研究ALF空间有重要作用。文献［3］给出了ALF空间中连续映射的定义：设X和Y是2个ALF空间，映射f：X→Y称为连续的，若开集的原像是开集。但是，由于任意x∈X（相应地，y∈Y）SN（x）（相应地，SN（y））都存在，则可以给出ALF空间的连续映射的等价刻画。

定义10 设X和Y是2个ALF空间，称映射F：X→Y是一个连续映射，如果对任意a∈X有F（SN（a，X））⊆SN（F（a），Y）。映射F：X→Y称为在点x∈X连续，如果F（SN（x，X））⊆SN（F（x），Y）。

与一般拓扑学中的连续映射相比，ALF空间的连续映射有其自身的特性：即使映射F：X→Y在点a∈X连续，F在SN（a）⊆X上也不一定连续。

例1 考虑图1a）中的SN（p），并且定义映射F：SN（p）→SN（p）为

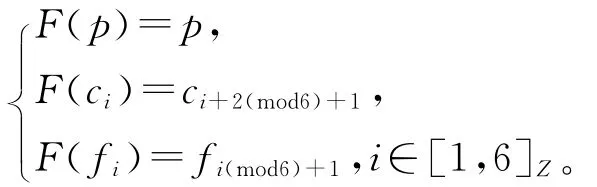
由于F（SN（p））⊂SN（p），所以映射F在点p连续，但在点ci和fi，i∈［1，6］Z不连续。例如，f1，f2∈SN（c1），而F（f1）和F（f2）不包含于SN（F（c1）），因此，F在点c1不连续。

下面介绍ALF空间中连续映射的性质（见图2）。

例2 1）ALF空间X上的常值映射是连续的。

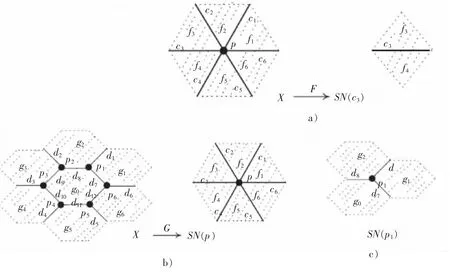
图2 ALF空间中的连续映射Fig.2 A continuous map between ALF spaces

2）考虑ALF空间X和图2a）中的SN（c3），其中，SN（c3）＝｛c3，f3，f4｝，X为图1a）中的SN（p），即X＝SN（p），映射F：X→SN（c3）定义为

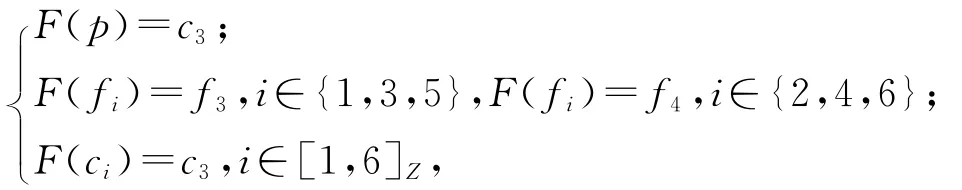
则F在SN（p）中连续。

3）在图2b）中，设X由六边形｛gi|i∈［0，6］Z｝中的7个点、线段｛di|i∈［1，12］Z｝中的12个点以及｛pi|i∈［1，6］z｝中的6个点构成，满足

定义映射G：X→SN（p）为

则映射G在X上连续。例如：验证G在g0和p1处的连续性如下：首先，由于SN（g0）＝｛g0｝，G（SN（g0））⊆SN（p），可知G在g0处连续。其次，由于SN（p1）＝｛g0，g1，g2，d7，d1，d8，p1｝（见图2c）），G（SN（p1））⊆SN（p），可知，G在p1处连续。

4）考虑图1a）中的SN（p）。定义G：SN（p）→SN（p）为G（p）＝p，G（ci）＝fi（mod6）＋1，以及G（fi）＝ci，i∈［1，6］Z。则G在任意ci（i∈［1，6］Z）处都不连续。

由定义10，可以得到以下性质。

1）设f：X→Y和g：Y→Z是ALF空间的连续映射，则复合映射g◦f：X→Z也连续。

2）任取a∈X，令F：X→Y是ALF空间的连续映射，则对于任意x，y∈SN（a，X）且y∈SN（x，X），都有F（y）∈SN（F（x），Y）。

同胚映射也是一般拓扑学的基本概念之一。2个空间称为同胚的或者拓扑等价的，如果存在从一个空间到另一个空间的连续双射，且它的逆映射也连续。然而，由于双射意味着有相同的元素个数，因此，这个定义不可能直接适用于2个不同元素个数的有限空间。

由于ALF空间的映射f的连续性与保持f的定义域的邻域关系相关，因此可以按如下方式定义ALF空间的同胚映射（见图3）。

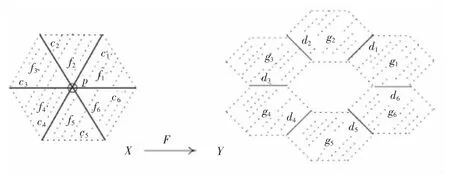
图3 ALF空间中的同胚Fig.3 A homeomorphism between ALF spaces

定义11 设X和Y是2个ALF空间，称F：X→Y是同胚映射，若F是连续双射，且它的逆映射也连续。若F：X→Y是ALF空间中的同胚映射，则记为X≈Y。

例3 如图3，令X＝XN（p）＼｛p｝，Y由去掉边界的六边形｛gi|i∈［1，6］Z｝的6个点以及去掉边界的线段｛di|i∈［1，6］Z｝的6个点组成，并且满足对任意的i∈［1，6］Z，SN（di）＝｛gi，di，gi（mod6）＋1｝，SN（gi）＝｛gi｝。

1）定义映射F：X→Y为F（ci）＝di，F（fi）＝gi，i∈［1，6］Z，则F是同胚映射。

2）在1）中，定义映射G：X→Y为G（ci）＝gi，G（fi）＝di，i∈［1，6］Z，则G不是同胚映射。事实上，虽然G是双射，但是G和G－1都不连续。

为了讨论ALF空间的局部性质，给出ALF空间的局部同胚（见图4）的定义。

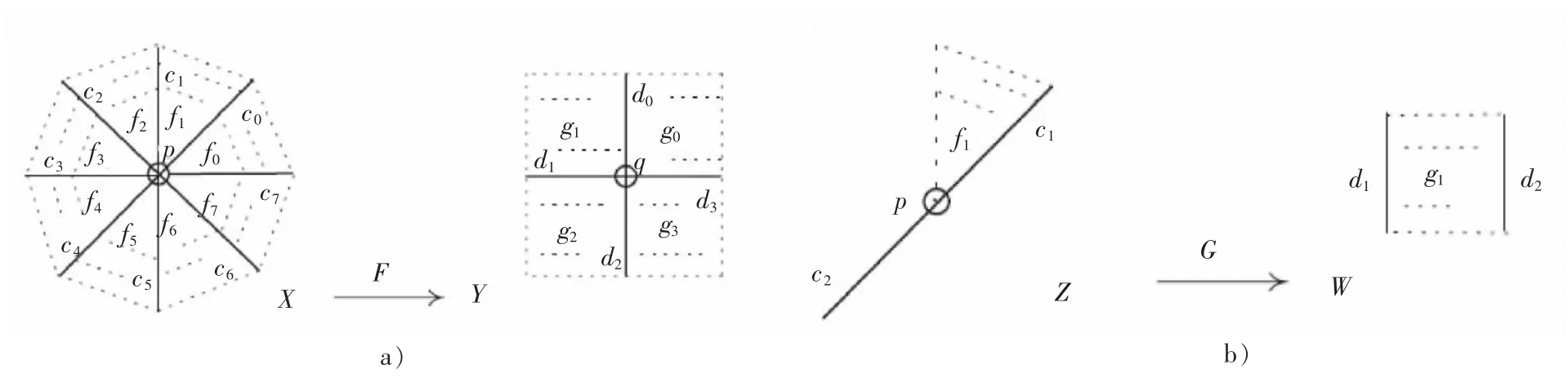
图4 ALF空间中的局部同胚Fig.4 A local homeomorphism between ALF spaces

定义12 设X和Y是2个ALF空间，称F：X→Y是局部同胚映射，若对任意x∈X，F在SN（x）上的限制，记为F|SN（x），是一个从SN（x，X）到SN（F（x），Y）上的同胚映射。

例4 1）在图4a）中，令X＝SN（p）＼｛p｝由去掉边界的三角形｛fi|i∈［0，7］Z｝的8个点以及去掉边界的线段｛ci|i∈［0，7］Z｝的8个点组成，并且满足对任意i∈［0，7］Z，SN（ci）＝｛fi，ci，fi＋1（mod8）｝，以及SN（fi）＝｛fi｝。令Y＝SN（q）＼｛q｝由去掉边界的长方形｛gi|i∈［0，3］Z｝的4个点以及去掉边界的线段｛di|i∈［0，3］Z｝的4个点组成，并且满足对任意i∈［0，3］Z，SN（di）＝｛gi，di，gi＋1（mod4）｝以及SN（gi）＝｛gi｝。

定义映射F：X→Y为F（ci）＝di（mod4），F（fi）＝gi（mod4），i∈［0，7］Z，则F不是同胚映射，但是是局部同胚映射。

2）在图4b）中，令Z由去掉边界的三角形｛f1｝的3个点以及去掉边界的线段｛ci|i∈［1，2］Z｝的2个点组成，并且满足SN（c1）＝｛f1，c1｝，SN（c2）＝｛c2｝以及SN（f1）＝｛f1｝。令W由去掉边界的长方形｛g1｝的一个点以及去掉边界的线段｛di|i∈［1，2］Z｝的2个点组成，并且满足SN（g1）＝｛g1｝以及SN（di）＝｛di，g1|i∈［1，2］Z｝。

定义映射G：Z→W为G（ci）＝di，i∈［1，2］Z，以及G（f1）＝g1，则G是一个连续双射，但是，G既不是局部同胚映射，也不是同胚映射。

由例3和例4，可以得到以下结论。

注1 ALF空间的同胚映射是局部同胚映射，反之不成立。

ALF空间的映射具有以下重要性质。

定理3 设X和Y是2个ALF空间，F：X→Y为映射。若F是局部同胚的双射，则F是同胚映射。

证明：只需证F的逆映射连续。任取b∈X，b的最小邻域为SN（b，X），令c＝F（b）∈Y，其最小邻域为SN（c，Y）。事实上，由于F在SN（b，X）上的限制（记为F|SN（b，X）：SN（b，X）→SN（F（b），Y）是同胚映射。F（SN（b，X））是c的最小邻域使得

由F－1和式（1），可以得到：

因此，F是同胚映射。

到此，证明了2个有限ALF空间同胚当且仅当它们有相同的元素。另外，还有另一种方法定义同胚，它直接适用于抽象胞腔复形，被称为组合同胚，它的定义基于胞腔的初等细分的概念（见文献［14］第24页）。更确切地说，一个欧氏复杂的三角剖分可以通过它的胞腔的初等细分的方法得到，而初等细分的概念可以应用到ALF空间。为了这个目的，一个ALF空间应被视为一个在文献［2］中定义的抽象多面复形（简称AC复形）。例如在三角测量的情况下，一个给定的AC复形可以通过一系列的胞腔的初等细分方法得到（更多内容参见文献［2］和文献［3］）。而文献［2］和文献［3］利用边界的关系定义了一个组合同胚，也可以按以下定义用邻域关系来表示。

定义13 2个抽象复形称为组合同胚的，如果它们拥有相同的三角剖分，或者更确切地说，存在三角剖分之间的保持邻域关系的双射。

这个定义与文献［15］中定义的同胚以及文献［10］、文献［11］和文献［12］中的数字同构都不相同。

注2 每一个同胚映射都是组合同胚映射，反之不成立。

4 ALF空间中连续映射的扩张

在第3节中提到，无论是在纯粹的拓扑理论中还是在应用拓扑理论（如数字拓扑）中，连续映射的扩张起到了非常重要的作用。因此，非常有必要研究ALF空间中连续映射的扩张问题，其方法和结果可用来研究LFS理论。事实上，HAN［4］和MELIN［7］在数字拓扑空间框架下讨论了若干类型的连续映射的扩张问题，并且从数字拓扑的角度建立了多种类型的收缩核。在本文中，ALF空间之间的连续映射与文献［4］和文献［7］中连续映射有明显不同，并且基于连续映射定义的收缩核和同胚也与文献［4］和文献［7］中相应的概念存在明显差异。确切地说，设X，Y，X′是ALF空间，F：X→Y是一个连续映射，称F′：X′→Y是F的扩张，如果F是F′在X⊆X′上的限制，记作F′|X。

下面介绍文献［6］中关于拓扑空间之间连续映射扩张的一个结论。

设（X′，T′）是一个拓扑空间，（X，T）是（X′，T′）的一个子空间，则（X，T）是（X′，T′）的收缩核当且仅当对任意的拓扑空间（Y，T″）以及连续映射f：（X，T）→（Y，T′），存在连续映射F：X′→Y使得F|X＝f。

由于ALF空间是以邻域为工具定义的，ALF空间之间的连续映射有自己独有的性质，并且连续映射的扩张也有自身的本质特征。因此，有必要讨论ALF空间框架下连续映射的扩张以及相应的收缩核（见图5）。

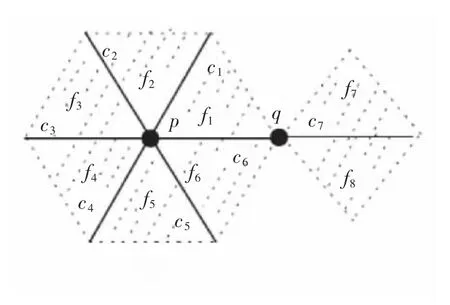
图5 ALF空间的收缩核Fig.5 A retract on ALF spaces

定义14 设X，X′是ALF空间，映射F：X′→X连续，称F是一个收缩映射，如果它满足：

1）X⊂X′；

2）∀x∈X，F（x）＝x。

相应地，称X是X′的一个收缩核，称元素x∈X′＼X相对于收缩核是可去除的。

例5 1）考虑图2a）中的空间SN（c3），单点集｛c3｝是SN（c3）的收缩核。

2）考虑图3中的空间X＝SN（p）＼｛p｝，X不是SN（p）的收缩核。下面采用反证法说明这一点。假设存在连续映射r：SN（p）→X使得r（x）＝x，则由r的连续性可知，r（p）∈X。方便起见，假设存在i∈［1，6］Z使得r（p）＝fi或者r（p）＝ci。

情形1：r（p）＝fi。对任意的i∈［1，6］Z，SN（fi）＝｛fi｝。从而，r（SN（p））⊆SN（fi）＝｛fi｝。显然，这与r（x）＝x矛盾。

情形2：r（p）＝ci。对任意的i∈［1，6］Z，SN（ci）＝｛fi（mod6）＋1，ci，fi｝。从而，r（SN（p））⊆SN（ci）。显然，r不是收缩映射。

3）考虑图5中的空间X，SN（p）是X的一个收缩核，相应的收缩映射r：X→SN（p）定义为

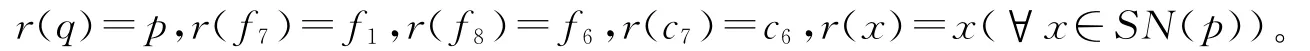
从例5对于ALF空间变形的研究中可以看出，收缩核的概念对于ALF空间的讨论是非常有用的。关于ALF空间收缩核的同胚性质，有如下结论。

命题1 设X，Y，X′是ALF空间，X是X′的一个收缩核，h：X′→Y是一个同态。则h（X）是Y的一个收缩核。

证明 令r：X′→X是ALF空间上的收缩映射。由于连续映射的复合仍然是连续映射，从而复合映射h◦r◦h－1是收缩映射。

例6 图6所示为ALF空间与收缩核相关的同胚。设X由4个六边形、一条割线和p1，p22个点构成，Y由1个平行四边形、1个梯形、1条割线和q1，q22个点构成。

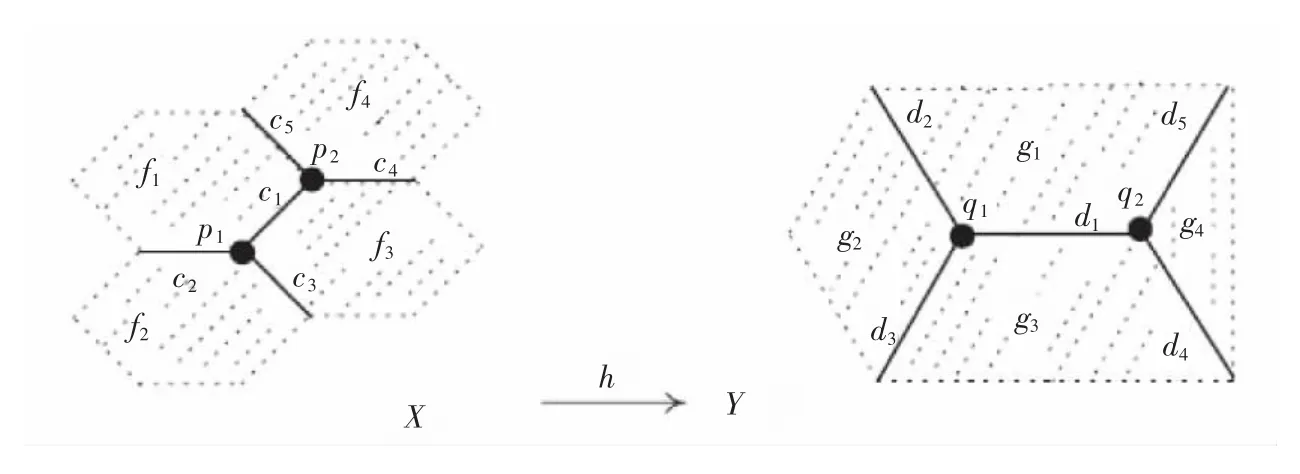
图6 ALF空间与收缩核相关的同胚Fig.6 A homeomorphism between ALF spaces in relation with a retract on ALF spaces

定义映射r：X→SN（p1）为

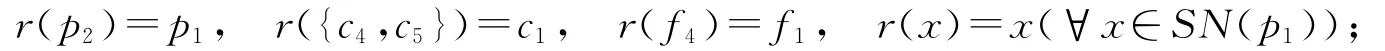
容易验证，SN（p1）是X的收缩核。进一步，考虑映射h：X→Y为

容易验证，SN（p1）是X的收缩核。相应的映射h：X→Y为

容易验证，h（SN（p1））＝Y＼｛q2，d4，g4，d5｝＝SN（q1）是Y的收缩核。相应的映射r1：Y→SN（q1）为

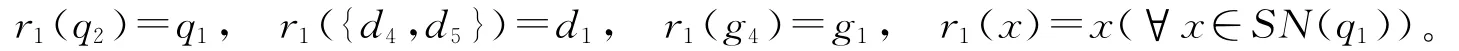
下面通过收缩核来研究ALF空间中连续映射的扩张问题。

定理4 设X，X′是ALF空间，则X是X′的一个收缩核当且仅当对任意的ALF空间Y以及任意的连续映射F：X→Y，存在连续映射G：X′→Y使得G|Y＝F。

证明 必要性：令r：X′→X是ALF空间上的收缩映射，f：X→Y是连续映射。则复合映射G：＝F◦r：X′→Y是连续映射，并且是F的扩张。

充分性：假设对任意的ALF空间Y，每个连续映射F：X→Y有一个扩张G：X′→Y，则恒等映射1X有扩张r：X′→X。因此，X是X′的收缩核。

例7 图7所示为ALF空间中连续映射扩张的不存在性，集合X＝SN（p）＼｛p｝，X′＝SN（p），集合Y由3个没有边的三角形和2条边构成，使得SN（d1）＝｛d1，g1｝，SN（d2，g1｝，SN（g1）＝｛g1｝。按照例5 2）中的讨论，X不是X′的收缩核。

图7 ALF空间中连续映射扩张的不存在性Fig.7 Non-existence of the extension of a continuous map between ALF spaces

定义映射G：X→Y为

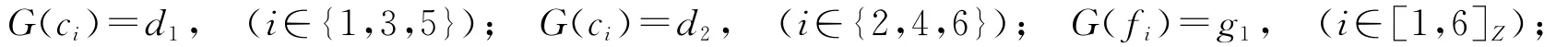
容易验证G是一个连续映射。但是，由于X不是X′的收缩核，所以不存在G的扩张G′：X′→Y使得G′|X＝G。以下采用反证法进行验证，假设存在G的扩张G′：X′→Y，由于SN（p）＝X′，所以G′（SN（p））∈Y且G′（SN（p））的最小邻域是Y。显然，Y中不包含这样的元素。这是一个矛盾。

5 结 语

对于ALF空间，研究了连续映射、同胚和局部同胚的一些性质；对于ALF空间的变形，定义和研究了与ALF空间中连续映射的扩张问题强相关的收缩核。对比一般的LFS理论，ALF空间理论能够更好地应用到计算机科学中去。

［1］ ALEXANDORFF P.Diskrete raume［J］.Mat Sb，1937，2：501-518.

［2］ KOVALEVSKY V.Axiomatic digital topology［J］.J Math Imaging and Vision，2006，26（1/2）：41-58.

［3］ KOVALEVSKY V.Geometry of Locally Finite Spaces［M］.Berlin：Publishing House，2008.

［4］ HAN Sangeon.Extension problem of several continuties in computer topology［J］.Bull Korean Math Soc，2010，47（5）：915-932.

［5］ KOVALEVSKY V，HAN Sangeon.Remarks on axiomatic locally finite space［J］.Theoretical Computer Science，preprint.

［6］ BORSUK K.Theory of Retracts［M］.Warsaw：Polish Scientific Publisher，1967.

［7］ MELIN E.Extension of continuous functions in digital spaces with the Khalimsky topology［J］.Topology and Its Applications，2005，153（1）：52-65.

［8］ SEIFERT H，THRELFALL W.A Textbook of Topology［M］.New York：Academic Press，1980.

［9］ ROSENFELD A.Connectivity in digital pictures［J］.J ACM，1970，17（1）：146-160.

［10］HAN Sangeon.Strong-deformation retract and its applications［J］.J Korean Math Soc，2007，44（6）：1479-1503.

［11］HAN Sangeon.Equivalent-covering and generalized digital lifting［J］.Information Sciences，2008，178（2）：550-561.

［12］HAN Sangeon.The-homotopic thinning and a torus-like digital image in［J］.J Math Imaging and Vision，2008，31（1）：1-16.

［13］KHALIMSKY E，KOPPERMAN R，MEYER P R.Computer graphics and connected topologies on finite ordered sets［J］.Topology and Its Applications，1991，36（1）：1-17.

［14］STILLWELL J.Classical Topology and Combinatorial Group Theory［M］.Michigan：Springer-Verlag，1995.

［15］HAN Sangeon.Continuities and homeomorphisms in computer topology［J］.J Korean Math Soc，2008，45（4）：923-952.

译者注：

拓扑学方法在大数据分析与研究中的应用是一个潜在和新颖的研究方向。由于距离函数是拓扑的一种重要研究对象，而在大数据分析和研究中又不可避免地涉及数据间的距离等问题，因此拓扑在大数据分析和研究中将具有重要作用。其实早在1985年，LEVOY等（LEVOY M，WHITTED T.The Use of Points as Display Primitives［R］.North Carolina：University of North Carolina at Chapel Hill，1985）就提出点云（point cloud）概念用于数据分析和研究。所谓点云，是指一个带有距离函数的有限集合，这种有限集合不同于通常的有限集合，主要指数据量特别大且用普通方法无法在短时间内实现遍历的集合，因此其思想方法和研究内容正好和大数据的特征相吻合。CARLSSON的文章（CARLSSON G.Topology and data［J］.Bulletin of the American Mathematical Society，2009，46（2）：255-308）对此作了全面的阐述。

Extension of continuity of maps between axiomatic locally finite spaces

HAN Sangeon
（Department of Mathematics，Institute of Pure and Applied Mathematics，Chonbuk National University，Jeonju 561-756，Korea）

The paper studies the extension problem of continuous maps between axiomatic locally finite spaces（for short，ALF spaces）.Indeed，an ALF space is a topological space satisfying a set of axioms suggested in［9，10］.Further，an ALF space is defined by using a special kind of neighborhood different from the topological neighborhood in classical topology so that the continuity of maps between ALF spaces can be defined by preserving the neighborhood relation（see Definition 10）.Therefore，it is necessary to develop the notions of continuity，homeomorphism and local homeomorphism for such spaces by using the neighborhood relation，which can be applicable in computer science.In the study of a deformation of an ALF space，we can develop a special kind of retract on ALF spaces.By using the retract，we can efficiently deal with the extension of continuous maps between ALF spaces.

locally finite space；axiomatic locally finite（ALF）space；smallest open neighbourhood；frontier；neighbourhood relation；homeomorphism；local homeomorphism；combinatorial homeomorphism；abstract cell complex；extension problem；retract

O189.1

A

1008-1542（2015）01-0081-09

10.7535/hbkd.2015yx01017

2014-11-12；

2014-12-16；责任编辑：王海云

韩相彦（1958—），男，韩国全北人，教授，主要从事数学拓扑理论方面的研究。

E-mail：sehan＠jbnu.ac.kr

韩相彦.公理化局部有限空间中映射连续性的扩展［J］.河北科技大学学报，2015，36（1）：81-89.

HAN Sangeon.Extension of continuity of maps between axiomatic locally finite spaces［J］.Journal of Hebei University of Science and Technology，2015，36（1）：81-89.

＊本文由姚卫和李云红翻译，原文发表于International Journal of Computer Mathematics，2011，88（14）：2889-2900.