摆动球轴承球与保持架碰撞行为

张文虎， 胡余生， 邓四二， 徐嘉， 李峰

(1.河南科技大学 机电工程学院， 河南 洛阳 471003；2.空调设备及系统运行节能国家重点实验室， 广东 珠海 519070；3.广东省制冷设备节能环保技术企业重点实验室， 广东 珠海 519070)

0 引言

在空间遥感器、卫星扫描装置、机器人以及航天飞机机体系统中，球轴承往往长期工作在往复摆动的模式下，其工作状态、碰摩行为和失效模式有别于恒速转动的轴承，常出现由于钢球与保持架频繁碰撞引发的保持架早期断裂，直接影响主机的使用寿命和可靠性。

Jiang等研究了摆动轴承的摩擦力矩，并分析摩擦力矩分量所占的比例，发现摆动轴承的摩擦力矩远大于恒速轴承。Komba等、Tonazzi等、Massi等开展深沟球轴承在摆动工况下的试验研究，分析了高负载下轴承的接触应力和摆动寿命。Ghezzi等试验研究了混合陶瓷球轴承与钢制球轴承的磨损情况，证明混合陶瓷球轴承抗磨损能力更强。Okorn等试验研究了非稳态载荷下摆动轴承的失效模式，阐明了轴承的失效机理。Glaeser分析了1 000余套重载脂润滑摆动滚子轴承的失效数据，将其主要失效模式归类为滚道和滚子工作表面的塑性流动、剥落、软化和磨损等。Stammler等试验研究了摆动幅值和频率对滚子轴承失效的影响，将不同的工况时间序列统计方法应用于风电轴承的寿命评估。

轴承在摆动过程中，保持架兜孔与滚动体发生剧烈碰撞，具有明显的冲击特征，引起保持架的断裂，因而研究摆动工况下钢球与保持架的碰撞行为十分重要。目前，国内外学者对滚动轴承保持架问题进行了大量研究。吴正海等、王春洁等、周延泽等理论分析了轴承转速、载荷、预紧量等因素对保持架稳定性以及保持架与滚动体碰撞力的影响。Cui等、邓四二等、孙雪等、Zhang等、李红涛等研究了工况参数、保持架结构参数、弹性支撑结构、润滑剂特性以及滚子动不平衡量对保持架质心轨迹、运行稳定性以及滚子与保持架碰撞力的影响。涂文兵等、罗丫等分析了加减速工况下径向载荷和轴向载荷对角接触球轴承钢球与保持架碰撞力的影响，发现较大的径向载荷和角加速度以及较小的轴向载荷均将导致减速与加速阶段轴承钢球与保持架碰撞力的增大。郑德志等、屈驰飞等研究了非稳态工况下高速球轴承运转性能和失效模式，研究结果表明：在不稳定状态下，钢球和保持架的碰撞加剧。摆动轴承元件的速度和受力均与恒速转动的轴承有很大不同。李峰等对摆动球轴承钢球的打滑行为和轴承摩擦力矩进行了分析。综上所述，国内外学者对摆动工况下球轴承的相关研究主要集中在摩擦力矩、打滑行为、使用寿命、失效模式及失效机理等方面，对轴承保持架与钢球碰撞行为的研究则主要集中在恒速、转速波动以及加减速等方面，缺少摆动工况下球轴承钢球与保持架碰撞行为的相关研究。

鉴于此，本文建立摆动球轴承动力学模型，开展轴承结构参数、工况参数和润滑剂拖动系数对钢球与保持架碰撞行为的影响研究，研究结果为轴承的工程应用、保持架结构设计以及润滑剂选取提供指理论支撑和评估方法。

1 摆动工况下深沟球轴承动力学分析模型

1.1 轴承坐标系

为准确描述轴承各元件的相对位置和相互作用关系，建立如图1所示的坐标系：固定坐标系、内圈坐标系、钢球质心坐标系、保持架质心坐标系和保持架兜孔坐标系

图1 坐标系Fig.1 Coordinate systems

1.2 轴承运动负载特性

如图2所示，外圈固定，内圈旋转，角速度为，摆动角度为，内圈承受径向载荷为轴承在摆动过程中，钢球的公转角速度和自转角速度取决于内圈的摆动速度和摆动方向。根据钢球进出承载区的情况，将钢球归类为始终位于承载区(状态1)、不断进出承载区(状态2)以及始终位于非承载区(状态3)3种状态。

图2 摆动工况下轴承运动负载状态Fig.2 Motion and load status of ball bearing during oscillating

内圈转速如图3所示，摆动周期由变速时间和稳定时间组成，从转速变化为-的时间为变速时间，持续工作在速度或-下的时间为稳定时间

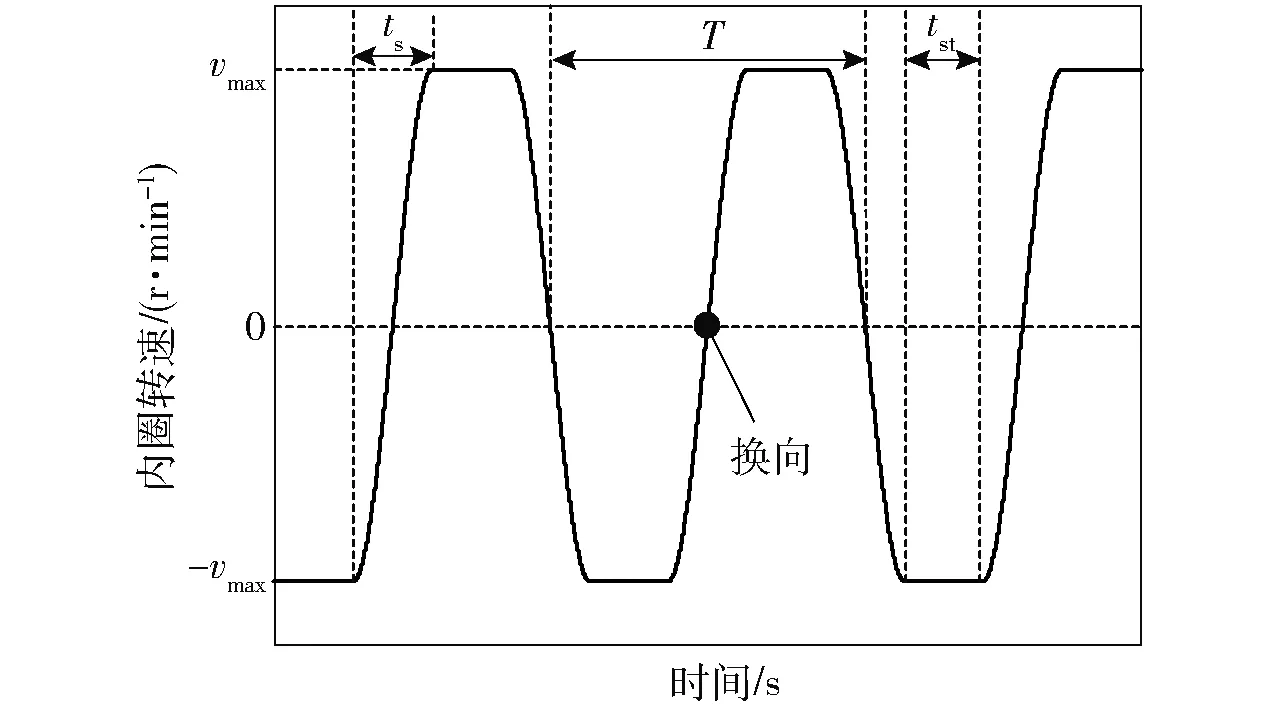
图3 内圈摆动速度Fig.3 Oscillating speed of inner ring

1.3 轴承各元件的动力学微分方程组

131 钢球动力学微分方程组

图4为钢球与滚道作用力示意图。图4中：下标i、e分别代表内套圈和外套圈；、、分别表示椭圆接触区域的长轴、短轴及法向；i为第个钢球的内接触角；e为第个钢球的外接触角；i、e分别为第个钢球与内、外沟道的法向接触力；Ri、Ri分别为第个钢球与内沟道接触入口区长轴方向及短轴方向的流体动压摩擦力；Re、Re分别为第个钢球与外沟道接触入口区长轴方向及短轴方向的流体动压摩擦力；i、i分别为第个钢球与内沟道长轴方向及短轴方向的拖动力；e、e分别为第个钢球与外沟道长轴方向及短轴方向的拖动力，方向由钢球与沟道接触界面的相对滑动速度方向决定。

图4 钢球与滚道作用力Fig.4 Acting force between ball and raceways

图5为钢球与保持架兜孔作用力示意图。图5中：c为第个钢球与保持架兜孔的碰撞力，与保持架兜孔坐标系的夹角为、、；R、R分别为第个钢球与保持架兜孔接触区入口处长轴方向及短轴方向的滚动摩擦力；S、S分别为第个钢球与保持架兜孔接触区入口处长轴方向及短轴方向的滑动摩擦力，其方向与钢球的自转速度方向有关。

图5 钢球与保持架兜孔作用力Fig.5 Acting force between ball and cage pocket

第个钢球的动力学微分方程组可表示为

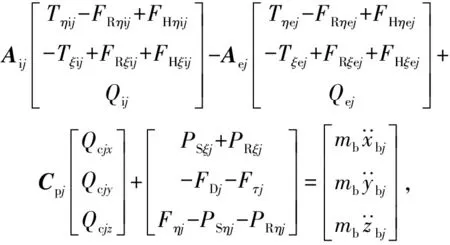
(1)

(2)

132 保持架动力学微分方程组

该类深沟球轴承保持架为球引导，且工作转速一般较低，故保持架的动力学微分方程组可表示为

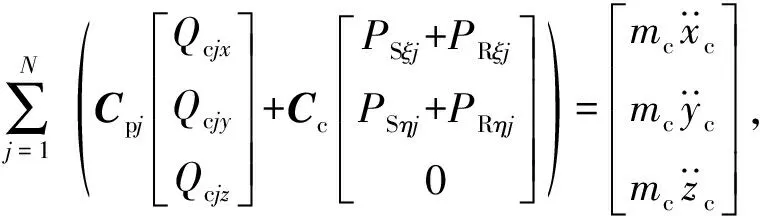
(3)

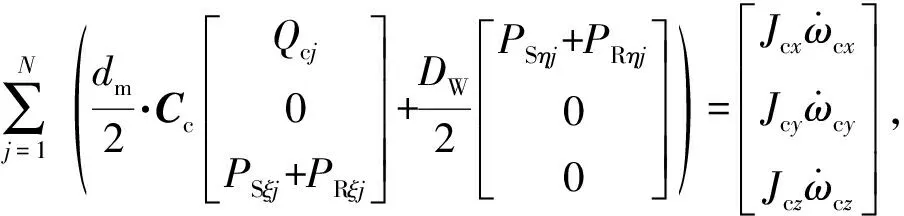
(4)

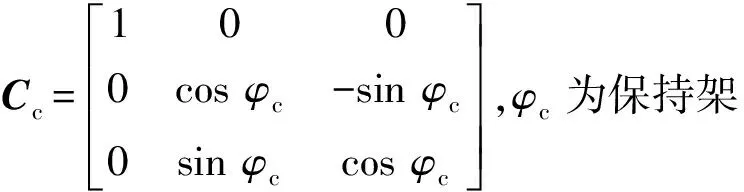
133 内圈动力学微分方程组

内圈动力学微分方程组可表示为

(5)

(6)

134 轴承变速判定方法及动力学微分方程组求解流程

1341 轴承变速判定方法

图6为一个摆动周期～内内圈和钢球的角速度变化示意图，根据内圈、钢球自转与钢球公转的关系，将一个摆动周期～分为～、～、～、～、～5个阶段。图7为轴承速度变化引起拖动力(即钢球与滚道间润滑剂的微摩擦力)方向变化的判定。图7中，为内圈接触点线速度，为钢球接触点线速度，为外圈接触点线速度，计算方法参见文献[25]。

图6 内圈和钢球的角速度变化示意图Fig.6 Change in angular velocities of inner ring and ball

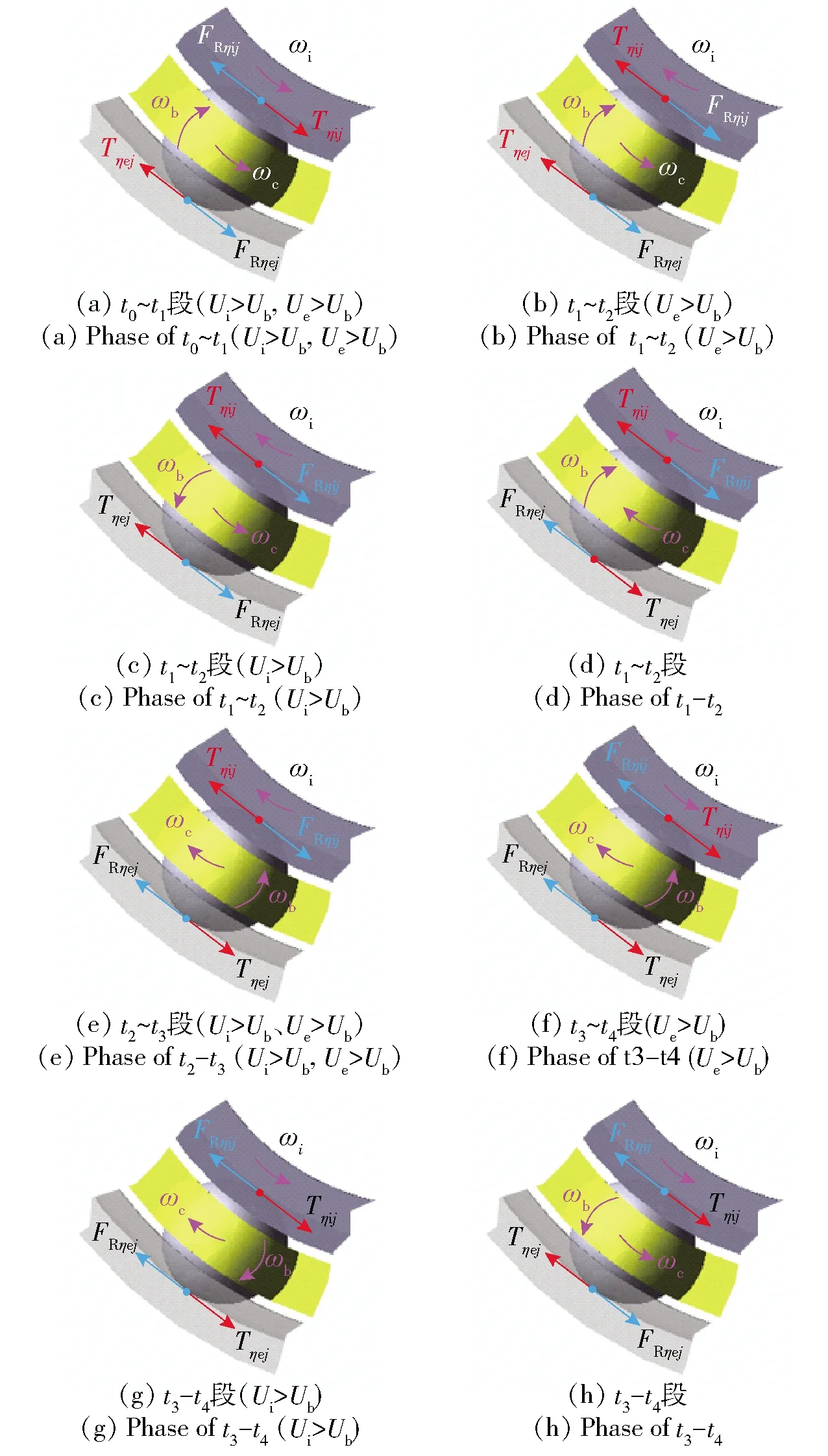
图7 拖动力方向判定Fig.7 Judgment of the direction of traction force

～段轴承各元件均沿反方向运动，当>、>时，拖动力的方向如图7(a)所示，反之，拖动力方向与图7(a)所示方向相反；点套圈换向之后正向旋转，但钢球由于惯性作用仍沿反方向运动，当>时，拖动力方向如图7(b)所示，当<时，钢球与外圈拖动力方向与图7(b)所示方向相反。由于套圈的拖动作用，钢球公转及自转速度均反向减小，若钢球公转为负而自转为正，则拖动力方向如图7(c)所示；若钢球自转为负而公转为正，则拖动力方向如图7(d)所示，点钢球公转与自转均达到正值。同样，～与～段拖动力方向判定分别如图7(e)～图7(h)。

图8 换向过程中的碰撞力Fig.8 Collision during swerve

轴承在变速与换向过程中，由于钢球与沟道和保持架间的相对速度发生变化，使钢球与沟道之间拖动力i、i、e、e的大小和方向、钢球与沟道接触入口区流体动压摩擦力Ri、Ri、Re、Re的大小和方向，以及钢球与保持架间碰撞力和摩擦力的大小和方向均发生变化。因此，摆动球轴承换向与变速过程同时影响(1)式～(6)式所示动力学微分方程组的力学参数与运动参数。

1.3.4.2 轴承动力学微分方程求解流程

轴承动力学微分方程求解流程如图9所示。输入轴承的材料参数、结构参数、摆动工况参数等，进行轴承拟静力学分析，得到各零件初始位置和运动参数的初始值，并采用Gear stiff(GSTIFF)变步长积分算法对(1)式～(6)式进行求解，求解初始步长为10s，相对误差为10. 如满足收敛条件，则输出轴承各元件的位置、速度、加速度等参数，根据相互作用力计算模型即可得到各元件之间的相互作用力，并将其作为下一步求解的初始值进行求解。如不满足收敛条件，则自动减小求解步长进行循环求解。

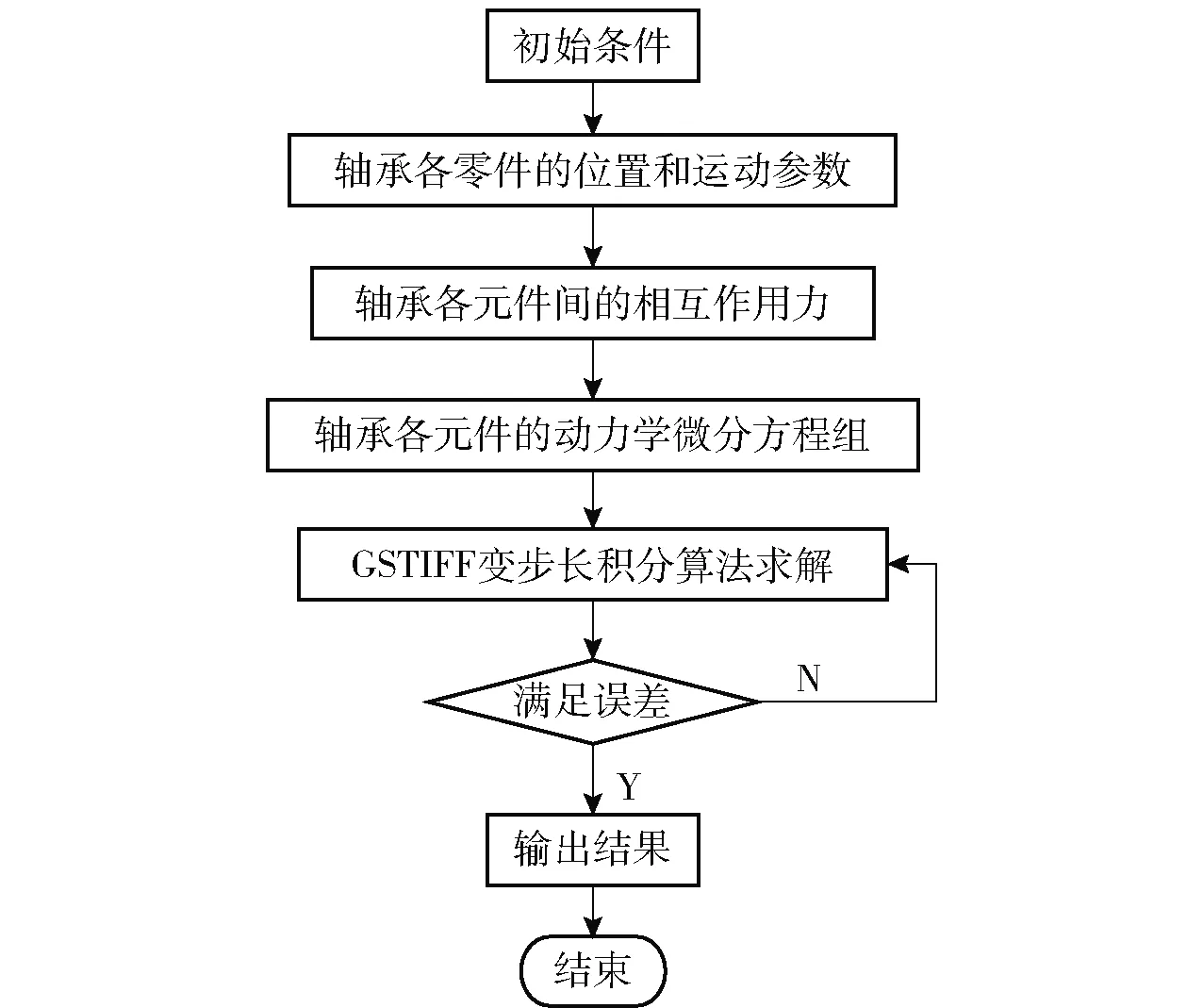
图9 求解流程Fig.9 Solution process

2 钢球与保持架碰撞行为研究

2.1 摆动与恒速下钢球与保持架碰撞行为对比分析

研究承载区(状态1)、不断进出承载区(状态2)以及非承载区(状态3)钢球与保持架碰撞力变化规律，轴承的参数如表1所示。

表1 轴承参数Tab.1 Bearing parameters

2.1.1 恒速下钢球与保持架碰撞力

图10为内圈恒速250 r/min、=3 000 N下钢球与保持架的碰撞力，由图中可知：承载区钢球推动保持架进行旋转，最大碰撞力为0.43 N；钢球由承载区进入非承载区期间，仍推动保持架进行旋转，但推动力快速减小；非承载区内钢球主要阻碍保持架旋转，但由钢球非承载区进入承载区期间，钢球开始推动保持架进行旋转。

2.1.2 摆动工况下钢球与保持架碰撞力

摆动周期=0.2 s，变速时间=0.01 s，稳定阶段内圈转速=250 r/min、=3 000 N工况下，钢球与保持架碰撞力在一个摆动周期内的变化如图11所示。

图10 恒速下钢球与保持架碰撞力Fig.10 Collision force between ball and cage at constant speed

图11 摆动工况下钢球与保持架碰撞力Fig.11 Collision force between cage and ball under the oscillating condition

由图11可知：承载区钢球与保持架的碰撞力最大值为66.76 N，不断进出承载区钢球与保持架碰撞力的最大值为45.98 N，非承载区钢球与保持架碰撞力最大值为17.79 N. 这是由于摆动内圈驱动承载区钢球进行旋转，钢球具有直接加减速度，使承载区钢球与保持架的碰撞力较大。而非承载区钢球则是保持架推动其进行旋转，因此非承载区钢球与保持架的碰撞力较小。由图10～图11可知，摆动工况下钢球与保持架的碰撞力远大于恒速下钢球与保持架的碰撞力。

2.2 保持架兜孔间隙对钢球与保持架碰撞力的影响

摆动周期=0.2 s，变速时间=0.01 s，稳定阶段内圈转速=100 r/min、=3 000 N工况下，保持架兜孔间隙对钢球与保持架碰撞力的影响如图12所示。

图12 保持架兜孔间隙对钢球与保持架碰撞力的影响Fig.12 Impact of cage pocket clearance on the collision force between cage and ball

图13为钢球与保持架碰撞力随保持架兜孔间隙的变化规律。随着保持架兜孔间隙的增加，钢球与保持架的碰撞力均不断增大。这是由于承载区钢球在内圈的驱动下加速旋转，兜孔间隙越大，钢球与保持架碰撞时的相对速度就越大，碰撞力也就越大。因此，较小的保持架兜孔间隙有利于减小摆动过程中钢球与保持架的碰撞力。

2.3 工况参数对钢球与保持架碰撞力的影响

2.3.1 拖动系数对钢球与保持架碰撞力的影响

摆动周期=0.2 s，变速时间=0.01 s，稳定阶段套圈转速=100 r/min，=3 000 N，不同拖动系数(即钢球与滚道间润滑剂的微摩擦系数)下钢球与保持架碰撞力如图14所示。

图15为钢球与保持架碰撞力随拖动系数的变化规律。随着拖动系数的增加，钢球与保持架碰撞力越大。这是因为轴承在换向时，较大的润滑剂拖动系数使得内圈对承载区钢球的拖动力变大，承载区钢球处于急加速或急减速的状态，承载区钢球与保持架的碰撞力也相应增加，进而引起保持架转速的突变，导致其他钢球与保持架碰撞力的增大。因此，为减小摆动工况下钢球与保持架的碰撞力，在保证轴承润滑的前提下，应选用低黏度润滑剂。

2.3.2 变速时间对钢球与保持架碰撞力的影响

摆动周期=0.2 s，套圈稳定阶段转速=100 r/min，=3 000 N，不同变速时间下钢球与保持架碰撞力的变化如图16所示。

图17为不同变速时间下钢球与保持架碰撞力变化规律。随着变速时间的增加，钢球与保持架的碰撞力均不断减小。这是因为变速时间越长，内圈换向时的加速度就越小，钢球与保持架的碰撞力也就越小。随着变速时间的增加，状态1和状态2钢球与保持架的碰撞力急剧减小。当变速时间大于0.03 s后，状态1和状态2钢球与保持架的碰撞力已基本稳定。

2.3.3 稳定转速对钢球与保持架碰撞力的影响

在摆动周期=0.2 s，变速时间=0.01 s，=3 000 N的工况下，内圈转速如图18所示，钢球与保持架碰撞力随轴承内圈稳定转速的变化规律如图19所示。

图13 不同保持架兜孔间隙下钢球与保持架 碰撞力变化规律Fig.13 Changing law of collision forces between cage and balls under the conditoins of various cage pocket clearances

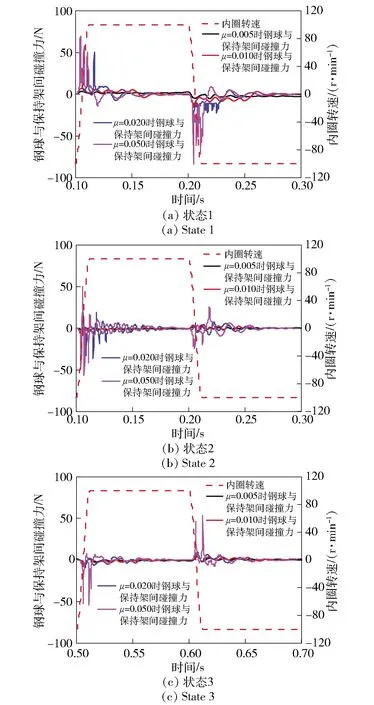
图14 拖动系数对钢球与保持架碰撞力的影响Fig.14 Impact of traction coefficient on the collision force between cage and ball

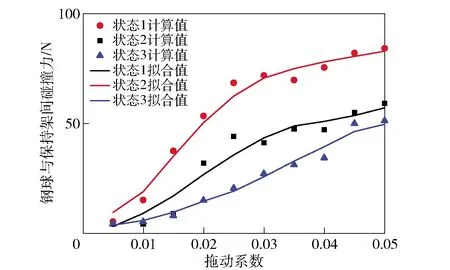
图15 不同拖动系数下钢球与保持架碰撞力的变化规律Fig.15 Changing law of collision force between cage and ball under the conditons of various traction coefficients

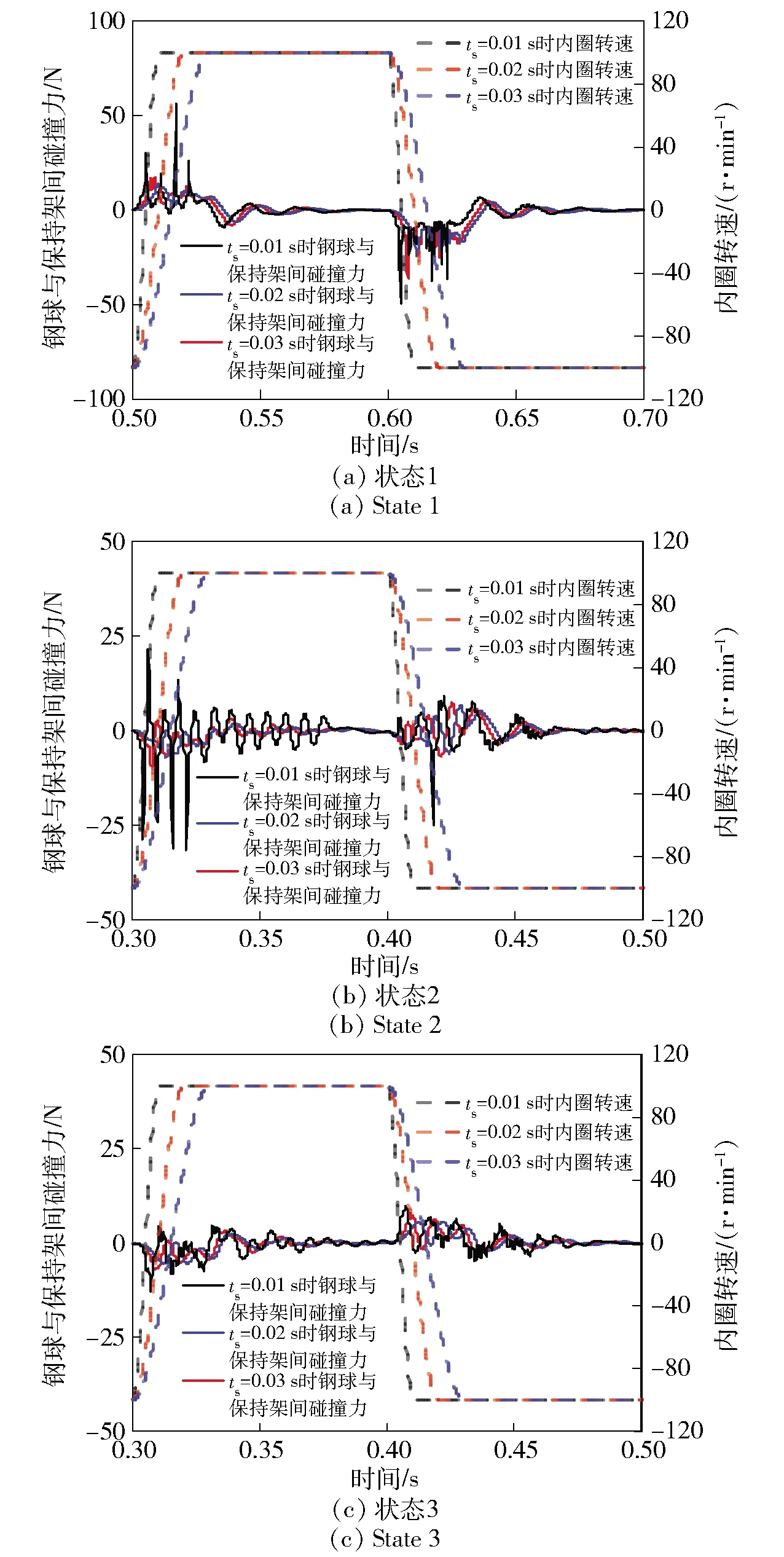
图16 变速时间对钢球与保持架碰撞力的影响Fig.16 Impact of shifting time on the collision force between cage and ball

图17 不同变速时间下钢球与保持架碰撞力的变化规律Fig.17 Changing law of collision force between cage and ball at the various shift times

图18 内圈转速Fig.18 Revolving speed of inner ring

图20为不同稳定转速下钢球与保持架碰撞力的变化规律。随着轴承稳定转速的增加，状态1和状态2钢球与保持架的碰撞力不断增大，状态3钢球与保持架碰撞力的大小变化不明显。且转速越高，钢球与保持架的碰撞冲击力越大，推动力与阻碍力作用时间越长，当稳定转速达到450 r/min时，在摆动周期内钢球与保持架始终存在相互作用。这是由于随着套圈稳定转速的增大，内圈换向加速度变大，钢球的速度变化越快，钢球与保持架碰撞力越大，使保持架转速快速增加，推动非承载区内的钢球旋转，非承载区钢球阻碍保持架旋转的作用力越大。

2.3.4 径向载荷对钢球与保持架碰撞力的影响

摆动周期=0.2 s，变速时间=0.01 s，稳定阶段套圈转速=100 r/min的工况下，不同位置处钢球的与保持架碰撞力随径向载荷的变化规律，如图21所示。

图22为不同径向载荷下钢球与保持架碰撞力的变化规律，由图可知，随着径向载荷的增加，钢球与保持架的碰撞力均不断增大。这是由于随着径向载荷的增加，承载区钢球受到内圈驱动的力也相应变大，保持架产生的加速度越大，因此保持架与钢球的碰撞力也越大。

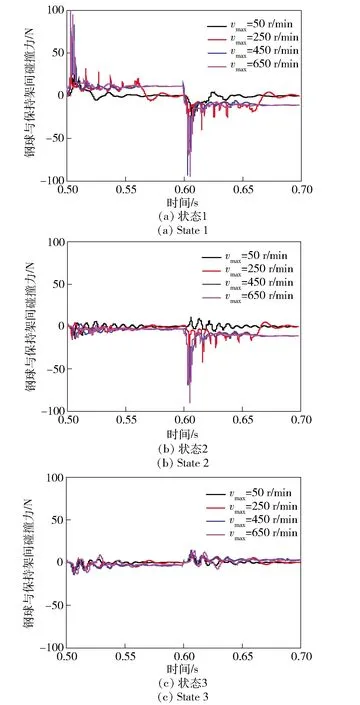
图19 稳定转速对钢球与保持架碰撞力的影响Fig.19 Impact of constant speed time on the collision forces between cage and balls

图20 不同稳定转速下钢球与保持架碰撞力的变化规律Fig.20 Changing law of collision force between cage and ball at various constant speeds

图21 径向载荷对钢球与保持架碰撞力的影响Fig.21 Impact of radial force on the collision force between cage and ball

图22 不同径向载荷下钢球与保持架碰撞力的变化规律Fig.22 Changing law of collision force between cage and ball under the various radial forces

3 结论

本文从理论分析角度阐明摆动工况下球轴承不同位置处钢球与保持架的碰撞行为，揭示了钢球与保持架的碰撞机理及影响钢球与保持架碰撞行为的关键因素。得出以下主要结论：

1)在摆动工况下，承载区钢球与保持架的碰撞力最大，不断进出承载区钢球与保持架的碰撞力次之，非承载区钢球与保持架的碰撞力最小，且摆动工况下钢球与保持架的碰撞力均远大于恒速工况下钢球与保持架的碰撞力。

2)随着保持架兜孔间隙的增加，钢球与保持架的碰撞力均不断增加；降低轴承的稳定转速、径向载荷、延长轴承变速时间以及采用低黏度的润滑剂均有利于减小摆动过程中钢球与保持架的碰撞力。