某全闭环操瞄系统的火炮身管指向控制研究

2015-11-19李伟杨刚陈腾飞韩崇伟

兵工学报 2015年9期

关键词：身管火炮车体

李伟，杨刚，陈腾飞，韩崇伟

（西北机电工程研究所，陕西咸阳712099）

某全闭环操瞄系统的火炮身管指向控制研究

李伟，杨刚，陈腾飞，韩崇伟

（西北机电工程研究所，陕西咸阳712099）

某履带式自行火炮的操瞄系统采用捷联惯导系统（SINS）测量火炮身管指向进行瞄准，使得高低伺服和方向伺服存在控制耦合，瞄准性能易受车体姿态影响。根据车体坐标系下的全闭环操瞄系统控制模型，对被控模型进行等效变换，得到平动坐标系下含非匹配不确定干扰的伺服被控模型，将原有的耦合干扰、建模误差等转换为各伺服分系统的外扰，分别对伺服分系统设计自抗扰控制器。自抗扰控制器可对外扰进行观测，并在非线性状态误差反馈控制器中进行补偿，克服外扰造成的伺服系统超调。在车体初始姿态分别为水平和倾斜6°条件下进行仿真，结果表明：与采用自适应滑模变结构控制相比，采用自抗扰控制策略的伺服瞄准系统实现了平稳、精确瞄准，超调小，有效地抑制了非匹配不确定干扰，且控制器输出平滑。

兵器科学与技术；自行火炮；捷联惯导系统；伺服系统；非匹配不确定；自抗扰控制

0 引言

全闭环伺服操瞄系统采用捷联惯导系统（SINS）直接测量火炮身管在地理坐标系下的指向［1］，以提高自行火炮的瞄准精度。该操瞄系统是由方向伺服和高低伺服组成的双轴伺服系统，可控制炮塔绕方向轴作回转运动，火炮身管绕俯仰（耳）轴作俯仰转动。方向伺服和高低伺服分别与SINS输出的航向角和俯仰角构成末端角位置闭环系统，用于火炮身管指向控制。与采用火炮车体坐标系下测角反馈的传统伺服操瞄相比，实现全闭环伺服操瞄的难点在于:惯导的安装方式造成方向伺服和高低伺服的控制不再独立，且都受车体姿态影响；车体为履带式底盘，采用油气悬挂，火炮身管在调转过程中的不平衡力矩易引起车体姿态变化，对伺服操瞄系统形成干扰，使火炮身管姿态更加难以控制。因此，建立包含车体姿态扰动的全闭环伺服操瞄控制模型十分必要。

文献［2］采用四元数法将大地坐标下的主令诸元转换为车体坐标系下各伺服分系统的控制指令，解决了全闭环伺服操瞄系统的坐标不统一问题。文献［3］将车体姿态扰动和坐标不统一视为对伺服位置控制干扰，提出了全闭环伺服串级控制方法，取得了一些效果。文献［4-6］对火炮身管指向控制进行了研究和探讨，但未涉及伺服系统及车体姿态的干扰问题。文献［7］针对姿态控制类连续非匹配不确定模型，提出了一种鲁棒反推滑模变结构控制方法，取得了良好的效果，但对离散反推滑模变结构控制的研究还需要取得突破［8］。

本文从工程应用出发，根据车体坐标系下的全闭环伺服操瞄控制原理，将该模型经等效变换至平动坐标系后，耦合干扰、未知干扰等可看作是各伺服分系统的总干扰，采用自抗扰控制［9］（ADRC）理论分别设计伺服分系统的控制器。ADRC的优点是不依赖系统精确的数学模型，它通过扩张状态观测器（ESO）对系统的总不确定扰动进行实时估计，并实施补偿，从而解决操瞄系统伺服控制的耦合干扰对瞄准性能的影响问题。

1 坐标系定义

SINS平行于火炮身管且固定于火炮耳轴上，随火炮身管转动，Ot为火炮身管质心，炮塔可绕方向回转轴左右转动，火炮身管在炮塔上可绕俯仰轴作上下起落运动，其简化图如图1所示。图中所涉及的坐标系包括大地坐标系、平动坐标系、地理坐标系和火炮身管俯仰部分坐标系。

大地坐标系Oxyz与大地固结不动，将原点O定为车体初始质心处，Ox轴平行于水平面指向正北，Oy轴平行于水平面指向正东，Oz轴垂直水平面向下。

平动坐标系O′x′y′z′原点为火炮身管在大地坐标系下调转的瞬时中心轴与火炮身管轴线的交点O′，O′x′轴与Ox轴指向一致，O′y′轴与Oy轴指向一致，O′z′轴与Oz轴指向一致。

地理坐标系Onxnynzn即捷联惯导导航坐标系，将原点On定为SINS所处位置点，Onxn轴平行于水平面指向正北，Onyn轴平行于水平面指正东，Onzn轴垂直水平面向下。

火炮身管俯仰部分坐标系Opxpypzp的原点Op为火炮俯仰转动（耳）轴与火炮身管俯仰平面的交点，Opxp轴与火炮身管轴线重合指向弹丸射向，Opyp轴与耳轴重合指向炮塔右侧，Opzp轴垂直于Opxp，与Opyp构成的平面指向下。

2 全闭环伺服操瞄系统控制模型

本文主要考虑火炮身管在调转过程中，因其质量偏心所产生的不平衡力矩影响车体姿态变化，它又通过炮塔干扰火炮身管在地理坐标系的指向。采用Langrange法建立履带式自行火炮车体及其悬挂、火炮俯仰部分等动力学模型，受篇幅限制，直接给出某履带式自行火炮车体坐标系的全闭环操瞄系统控制原理见图2.

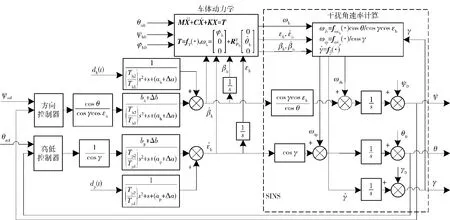
图2 车体坐标系下的全闭环伺服操瞄系统控制原理图Fig.2 Control principle diagram of closed-loop servo system in car body coordinates

图2中ψb、θb0、φb0分别为车体初始航向角、俯仰角、横滚角；车体动力学方程中X为包含了车体姿态角φb、θb等的动力学方程状态变量矩阵（在调炮过程中，假设车体航向角ψb不变）；M为车体质量、悬挂和主轴转动惯量矩阵；C为车体悬挂的阻尼矩阵，K为车体悬挂的刚度矩阵，其具体形式参考相关文献［10-11］；T为车体动力学干扰力矩输入矩阵，它是以火炮身管俯仰部分和炮塔的结构参数、调炮角度βb、εb、调炮角速度、车体角速率和角加速度等变量的函数fT（·）；ψ、θ、γ分别为SINS的航向角、俯仰角和横滚角，其值的解算为火炮身管指向解算模型，它是根据SINS的欧拉角法航姿解算原理得到；ωip、ωih分别为俯仰和方向伺服的空间速度耦合干扰，分别是以等为变量的函数fωip（·）、fωih（·），二者相互关联，且跟车体姿态角φb、θb有关，易造成方向伺服系统超调大，调节时间长；ψref、θref分别为方向和高低伺服的控制指令；被控模型、分别为方向伺服的永磁交流同步电机（PMSM）驱动系统及其炮塔、高低伺服的PMSM驱动系统及其火炮身管俯仰部分的传递函数，其中:bh、bp分别为伺服被控对象的方向、高低控制增益；Δah、Δap、Δbh、Δbp分别为不确定项；Th1、Th2、Tp1、Tp2分别为方向、高低伺服被控对象的1阶、2阶时间常数，且Th1≥Th2，Tp1≥Tp2；ah=1/Th1，ap= 1/Tp1.火炮身管高低角变化会影响方向伺服系统的转动惯量，从而影响Th1、Th2值大小，但其变化是有界的。为了使伺服位置环开环增益保持恒定，便于后续控制模型变换，在高低驱动环节前乘1/cos γ，在方向驱动环节前乘cos θ/（cos γcos εb）。

通常在位置控制器设计时，将高阶略去，将驱动部分简化为1阶惯性环节。根据图2，操瞄系统的方向伺服和高低伺服的控制模型忽略高阶项后，均可简化为以下非匹配不确定控制模型:

式中:dh（t）、dp（t）分别为未知干扰，t为时间；Δh、Δp分别为高阶未建模动态；ωih、ωip为有界非匹配不确定项；yh、yp分别为各伺服系统测量输出。操瞄被控模型第（1）式、（2）式的第一式为地理坐标系下的运动方程，且存在非匹配不确定项；第二式为伺服驱动模型。该模型会给应用ADRC带来困难，需要对该模型进行等效变换。

由于大地坐标系、平动坐标系、地理坐标系3系平行，且无相对转动，根据欧拉定理，火炮身管轴线从tk-1时刻的指向调转至tk时刻的指向，其转动可等效成绕大地坐标系中某瞬时中心轴转过某角一次完成，并不关心转动中间过程。因此，可将瞬时中心轴分解至平动坐标系中，被控模型也就等效变换至平动坐标系下，令ωβ+ωih=ωψ，ωε+ωip=ωθ，得

式中:ωψ、ωθ可看作火炮身管在平动坐标系分别绕O′z′、O′y′1转动角速率，而O′y′1为O′y′绕O′z′转动ψ角得到，见图3，O′xp为火炮身管轴线；dψ、dθ分别为平动坐标系下的方向伺服和高低伺服的非匹配有界未知干扰总和:

图3中将原来在车体坐标系下控制火炮身管绕方向轴和俯仰轴转动，以及车体姿态变化引起的火炮身管转动，转换为直接控制火炮身管在平动坐标系下绕O′z′轴、O′y1轴转动实现火炮瞄准。同时，原模型的耦合干扰、外界未知扰动之和转换为平动坐标系下高低和方向伺服系统各自控制通道的总干扰，且被控对象的增益和时间常数都未发生变化，只是等效的干扰复杂化。因此，各伺服分系统可分别单独设计ADRC控制器，对应用ADRC控制器的全闭环伺服瞄准系统控制原理在图2基础上稍加修改仍可适用。

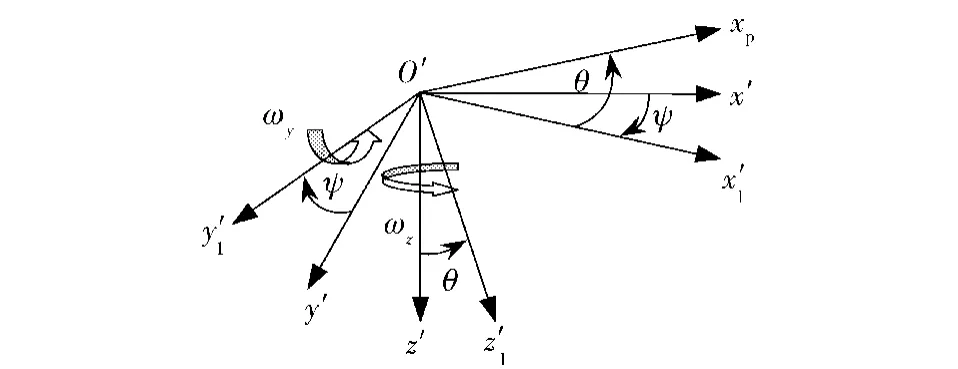
图3 平动坐标系与火炮身管轴线的关系Fig.3 Relationship between geographic coordinates and gun tube axis

3 伺服自抗扰控制器设计

对扰动作用下的全闭环操瞄伺服分系统，采用ADRC实现操瞄系统火炮身管空间角度指向控制。ADRC控制策略主要由跟踪微分器（TD）、ESO、非线性状态误差反馈控制器（NLSFF）组成［12］，其结构如图4所示。

图4 2阶ADRC控制结构图Fig.4 Structure of second-order ADRC

为了便于应用计算机控制，采用离散ADRC.2阶离散TD形式为

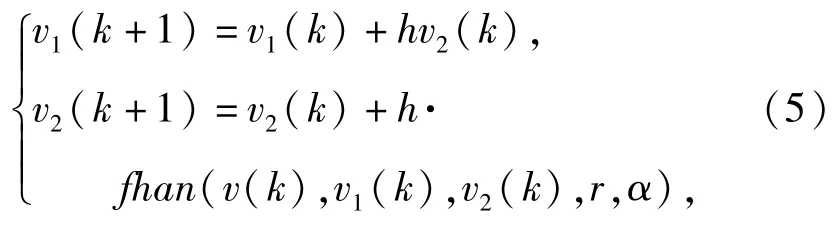
式中:h为积分步长；k为计算步数；v为控制指令，对高低伺服取高低调转指令θref，对方向伺服取方向调转指令ψref；v1为v的跟踪信号；r为速度因子；v2是v1的导数；α为滤波因子；fhan（·）为最速控制综合函数，其中:

3阶离散非线性ESO形式为

式中:y为量测输出，对高低伺服取捷联惯导的俯仰角θ，对方向伺服取捷联惯导的航向角ψ；z1为对y观测输出；e为观测误差；z2为对的观测；z3为对系统干扰量的观测；f0（·）为模型确知部分；u为控制输入；β01、β02、β03分别为观测器增益；fal（·）为非线性函数，

其中:α、δ为常数。fal（·）也可以具有其他的形式。

离散NLSFF形式为

式中:β1、β2分别为非线性反馈控制律增益；可调参数α1、α2的取值范围为0＜α1＜1＜α2，且α2=2α1；b0为伺服驱动增益，对方向伺服取bh，对高低伺服取bp.由于实际应用时该ADRC控制器是采用1阶欧拉方法对连续ADRC进行离散化，为了能使离散后的ADRC保持原有的性能，采样周期尽量短。

4 仿真验证

自行火炮驻停时车体航向为ψb=80°；火炮在车体系下的初始角度分别为:方向角βb=0°，高低角εb=0°.高低伺服和方向伺服的驱动传递函数分别为:bh=337，bp=523，Th1=0.04，Th2=0.001 6，Tp1=0.025，Tp2=0.005，Δah=1，Δap=0.1，Δbh=4，Δbp=10，以上参数是高低角εb=0°时辨识得到。高低调转指令θref=1 000 mrad，方向调转指令ψref= 2 500 mrad.设定未知扰动dp（t）=0.1sin（2πt），dh（t）=0.1sin（2πt）.高低伺服ADRC控制器的TD参数为:控制步长h=0.001 s，r=2 000，d=0.01；ESO参数为:控制步长h=0.001 s，δ=0.0045，b0=523，β01=1 000，β02=6 324.6，β03=7 962.1；NLSFF控制参数为:α1=0.6，α2=1.2，β1=0.7，β2=0.02，δ= 0.001，b0=523.方向伺服ADRC控制器的TD参数为:控制步长h=0.001 s，r=10 000，d=0.01；ESO参数为:控制步长h=0.001 s，δ=0.004 5，b0=323，β01=1 000，β02=6 324.6，β03=13 270.NLSFF控制参数为:α1=0.6，α2=1.2，β1=0.45，β2=0.001，δ= 0.01，b0=323.为了比较ADRC控制效果，可将其与采用自适应滑模变结构控制器［13］（简称VSC）时的系统进行对比。其高低伺服VSC最佳参数分别为:cp=14，qp=25；方向伺服VSC最佳参数分别为ch=19.5，qh=5；控制步长Ts=0.001 s.很容易验证VSC对满足匹配不确定干扰的系统具有良好的静态、动态性能，控制输出无抖振。采用两种控制方法分别在车体初始姿态水平（θb=0°、φb=0°）和车体初始姿态倾斜6°（θb=6°、φb=6°）的情况下进行仿真，得到结果如图5～图10所示。

各伺服分系统ADRC的ESO对相应伺服分析系统在平动坐标系下的调炮角速度ωψ、ωθ，以及总干扰dψ、dθ估计结果见图5，其ESO能够估计到总干扰dψ、dθ，其值随调转过程结束而趋于0.被估计的总干扰峰值出现在另一个控制通道的制动初始时刻，车体越倾斜，干扰越大。

使用ADRC控制下的车体姿态变化见图6.车体姿态变化随着伺服系统调转控制结束也趋于稳定至定值，伺服系统调转制动加速度对车体姿态而言是较大的扰动。同时，车体姿态变化也是瞄准系统的扰动，由于车体悬挂系统的弹性变形导致车体姿态变化，放大了对操瞄控制系统的扰动。

图5 采用ADRC控制时ESO对高低角和方向角调转速度和总干扰的观测结果Fig.5 Observed results of elevation angle shift speed，azimuth angle shift speed and total interference when using ESO in ADRC

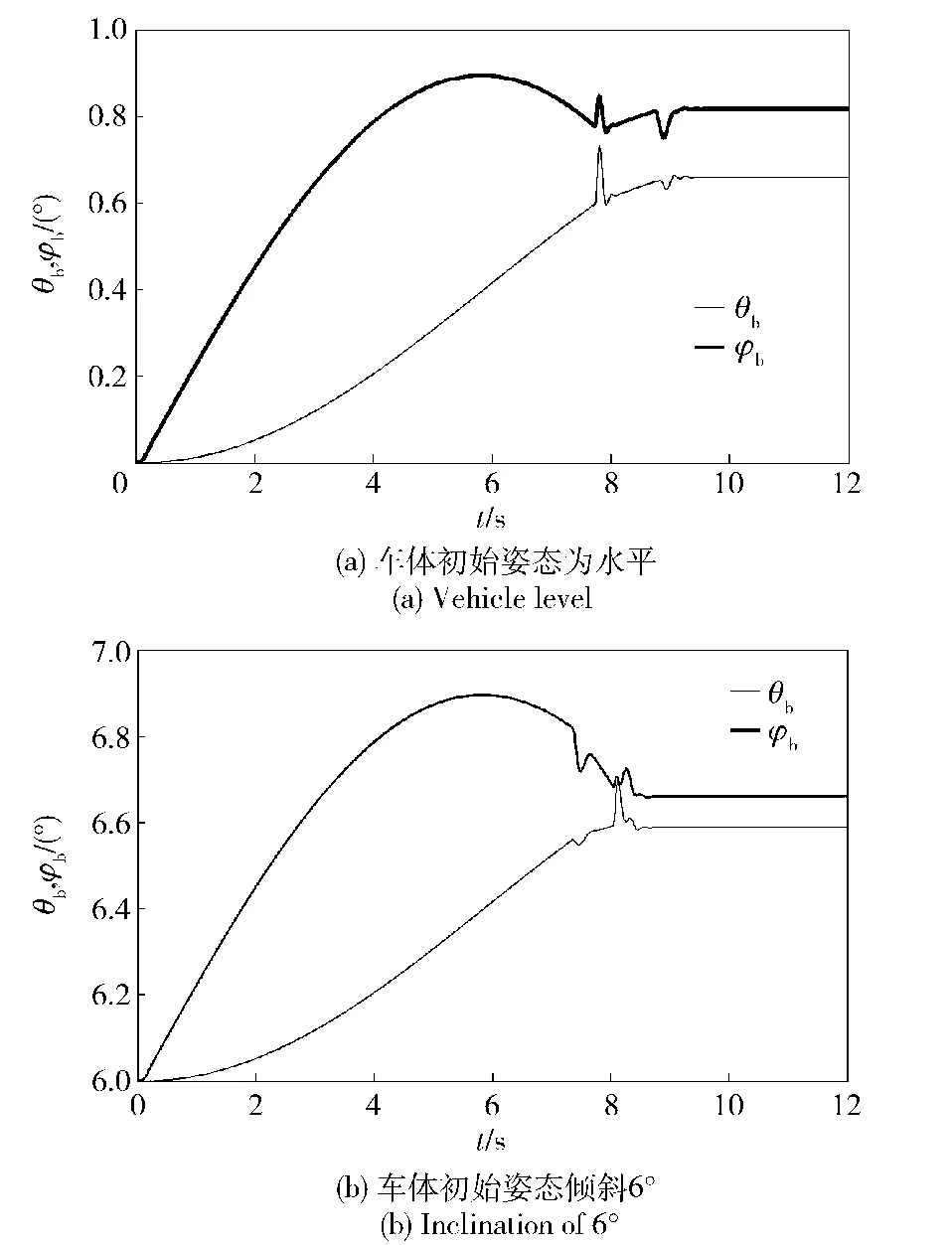
图6 采用ADRC控制时的车体姿态角输出Fig.6 Outputs of vehicle attitude angle when using ADRC

平动坐标系下分别采用ADRC和VSC控制时的各伺服分系统的角度调转见图7和图8，两种控制方法的控制量输出见图9和图10.对于高低伺服系统无论是车体处于水平还是倾斜状态下，采用ADRC和VSC的控制效果区别不大。而对于方向伺服系统，采用VSC控制时方向角超调较大，约20 mrad，表明干扰对平动坐标系下的调转起了加速作用。采用ADRC时的超调小得多，说明对干扰补偿有效，且未引起车体姿态振荡，车体姿态平稳变化趋于稳定。当调转误差不大于0.1 mrad，略快于VSC控制0.5 s调转到位。比较图9（b）和图10（b），为了克服不确定干扰，ADRC控制器输出变化大于VSC控制器输出变化。ADRC即使是在较大的干扰下，其输出平滑无抖振，而VSC的自适应趋近率已经不能消除抖振，且干扰越大，VSC控制器输出越抖振，说明伺服系统的干扰dψ、dθ为非匹配不确定干扰。

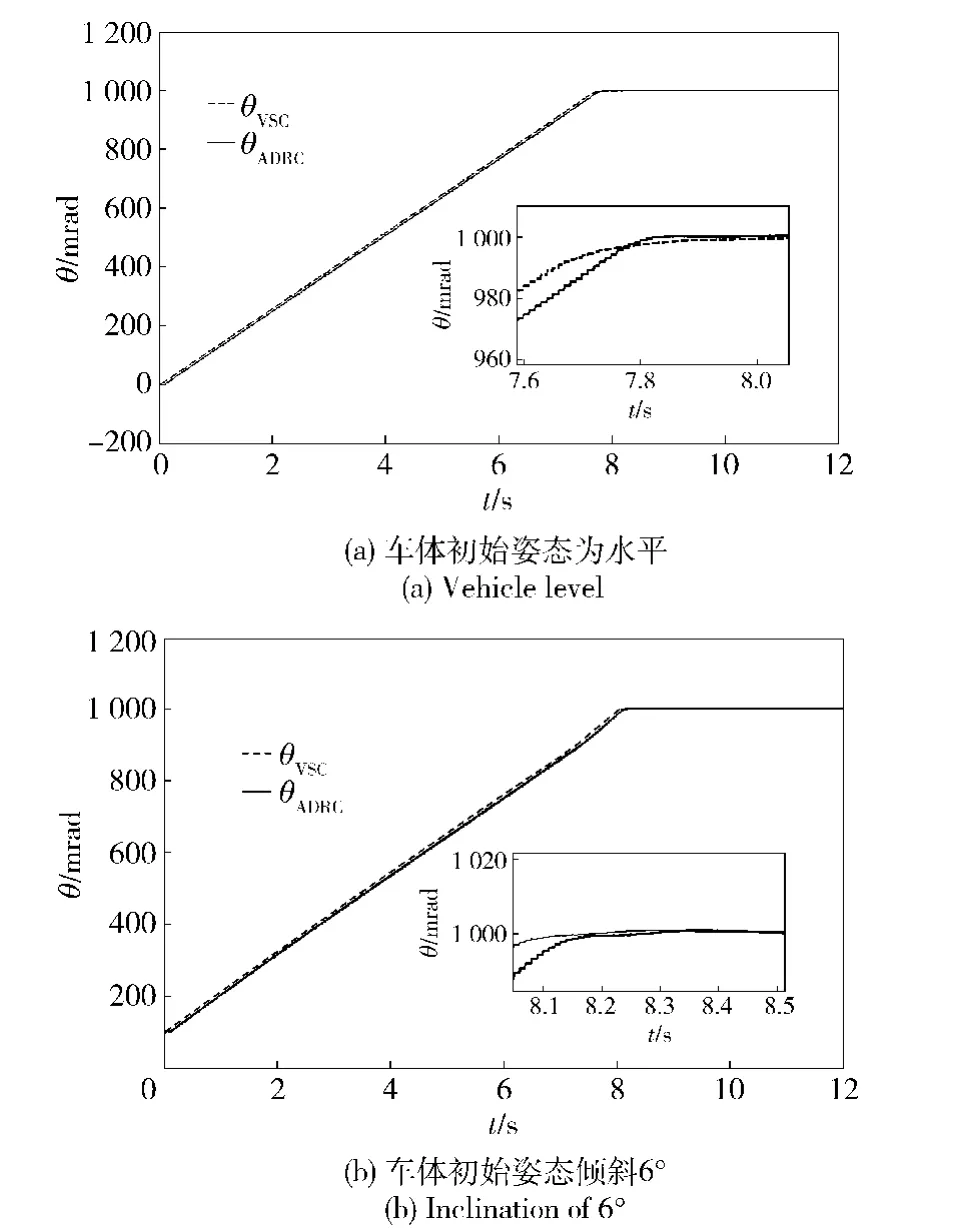
图7 平动坐标系下分别采用VSC和ADRC控制时的高低角输出Fig.7 Outputs of elevation angle when using VSC and ADRC in quasi geodetic coordinates

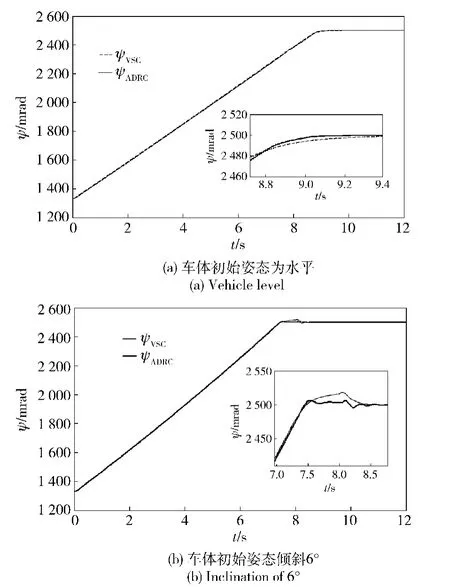
图8 平动坐标系下分别采用VSC和ADRC控制时的方向角输出Fig.8 Outputs of azimuth angle using VSC and ADRC in quasi geodetic coordinate systems

5 结论

考虑到全闭环操瞄控制系统中的各伺服分系统车体坐标系下存在速度耦合干扰问题，对该被控模型进行等效变换至平动坐标系后，可将伺服分系统之间的耦合扰动转换为伺服各分系统的总干扰。由此可按独立子系统性能要求单独设计ADRC控制器，利用ADRC控制器的ESO对伺服各分系统的总干扰进行观测，并在NLSFF进行补偿。研究结果表明，设计的ADRC控制器使全闭环伺服操瞄系统能在有限时间内实现平稳、精确瞄准，超调小，有效地抑制了非匹配不确定干扰，且控制器输出平滑无抖振。该模型的建立和控制方法的应用为此类系统的研究提供了一种新途径。

（

）

［1］严德斌，胡朝根，陈红军.基于激光陀螺捷联惯导技术的火炮身管指向系统设计［J］.舰船电子工程，2011，31（9）:57-59. YAN De-bin，HU Chao-gen，CHEN Hong-jun.Design of gun turntable system based on ring laser gyro strap-on inertial navigation system［J］.Ship Electronic Engineering，2011，31（9）:57-59.（in Chinese）

［2］李伟，饶蔚巍，韩崇伟，等.基于捷联惯导的火炮随动系统应用研究［J］.火炮发射与控制学报，2009（1）:35-38. LI Wei，RAO Wei-wei，HAN Chong-wei，et al.Application research of gun servo system based on strapdown inertia navigation system［J］.Journal of Gun Launch&Control，2009（1）:35-38.（in Chinese）

［3］李伟，韩崇伟，周文，等.全闭环炮控伺服串级控制研究［J］.系统仿真学报，2013，25（2）:296-300. LI Wei，HAN Chong-wei，ZHOU Wen，et al.Study on cascade control for all closed-loop gun control servo［J］.Journal of System Simulation，2013，25（2）:296-300.（in Chinese）

［4］胡田，付庆红，佟俐.刚体姿态控制在火炮自动操瞄中的应用［J］.火力与指挥控制，2009，34（12）:148-150. HU Tian，FU Qing-hong，TONG Li.Application of rigid body attitude control in gun's automatic aiming［J］.Fire Control&Command Control，2009，34（12）:148-150.（in Chinese）

［5］ Gu Y L，Loh R N K，Coleman N.Control of weapon pointing systems base on robotic formulation［C］∥Proceeding of the 1992 A-merican Control Conference.Chicago，IL，US:IEEE，1992: 413-418.

［6］田建辉，钱林方，徐亚栋，等.无人炮塔火力线跟踪神经滑模控制［J］.兵工学报，2011，32（6）:641-645. TIAN Jian-hui，QIAN Lin-fang，XU Ya-dong，et al.Neural sliding mode control for tracking of axis of firepower of unmanned turret［J］.Acta Armamentarii，2011，32（6）:641-645.（in Chinese）

［7］王坚浩，胡剑波.一类非匹配不确定非线性系统的鲁棒跟踪控制［J］.控制与决策，2011，26（5）:727-731. WANG Jian-hao，HU Jian-bo.Robust tracking control for a class of nonlinear systems with unmatched uncertainties［J］.Control and Decision，2011，26（5）:727-731.（in Chinese）

［8］胡剑波，李飞，魏高乐，等.不确定系统反推滑模变结构理论及其应用［J］.系统工程与电子技术，2014，36（3）:520-526. HU Jian-bo，LI Fei，WEI Gao-le，et al.Theory and applications of backstepping sliding mode variable structure controlfor uncertain systems［J］.Systems Engineering and Electronics，2014，36（3）: 520-526.（in Chinese）

［9］韩京清.自抗扰控制技术——一种补偿不确定因素的控制技术［M］.北京:国防工业出版社，2009. HAN Jing-qing.Active disturbance rejection control technique-the technique for estimating and compensating the uncertainties［M］. Bejing:National Defense Industry Press，2009.（in Chinese）

［10］喻凡.车辆动力学及其控制［M］.北京:机械工业出版社，2013:174-182. YU Fan.Armored vehicle dynamics and control［M］.Beijing: China Machine Press，2013:174-182.（in Chinese）

［11］ Ikenaga S，Lewis F L.Active suspension control of ground vehicle based on a full-vehicle model［C］∥Proceedings of 2000 American Control Conference.Chicago，Illinois，US:IEEE，2000: 4019-4024.

［12］韩京清.从PID到自抗扰控制技术［J］.控制工程，2002，9（3）:13-18. HAN Jing-qing.From PID technique to active disturances rejection control technique［J］.Control Engineering of China，2002，9（3）:13-18.（in Chinese）

［13］翟长连，吴智铭.不确定离散时间系统的变结构控制［J］.自动化学报，2000，26（2）:184-191. ZHAI Chang-lian，WU Zhi-ming.Variable structure control designed for uncertain disctrete time systems［J］.Acta Automatica Sinica，2000，26（2）:184-191.（in Chinese）

Research on Gun Pointing Control of a Full Closed-loop Aiming System

LI Wei，YANG Gang，CHEN Teng-fei，HAN Chong-wei
（Northwest Institute of Mechanical and Engineering，Xianyang 712099，Shaanxi，China）

A strapdown inertial navigation system（SINS）is used to measure the pointing of gun barrel for aiming for a tracked self-propelled gun.However，it causes the control coupling of pitching servo and azimuth servo，and the aiming accuracy can be easily affected by vehicle posture.According to the full closed-loop aiming system model under vehicle coordinates，the servo control model under quasi geodetic coordinates including the disturbance of mismatched uncertainty is obtained.Active disturbance rejection controllers（ADRCs）are designed for each axial servo system，considering the coupling and modeling errors to be external disturbance.ADRC can observe the external disturbance and compensate the nonlinear state error feedback controller to eliminate the overshoot caused by it.Thef servo aiming system is simulated under the conditions of initial attitude of vehicle level and inclination of 6 degree.The results show that，compared with the adaptive sliding mode variable structure control，the servo system using ADRC strategy obtains more steady and more accurate targeting results，and gets smoother controller output，meanwhile suppresses the unmatched uncertain interface effectively.

ordnance science and technology；self-propelled gun；SINS；servo system；unmatched uncertainty；active disturbance rejection controller