基于三次样条插值的硅压阻式压力传感器的温度补偿*

王冰冰，李淮江

（淮北师范大学物理与电子信息学院，安徽 淮北 235000）

基于三次样条插值的硅压阻式压力传感器的温度补偿*

王冰冰，李淮江*

（淮北师范大学物理与电子信息学院，安徽 淮北 235000）

传感器的零点温度漂移、灵敏度温度漂移和非线性误差是影响传感器性能的主要因素，如何能使该类误差得到有效补偿对于提高其性能有重要意义。提出了基于三次样条曲线插值的温度补偿方法，改进了传统三次样条曲线插值的补偿方法，分别对传感器的零点、灵敏度以及非线性进行补偿，用这种方法对测压范围为1.014 0×105Pa～3.014 0×105Pa，温度范围为-20℃～+60℃的硅压阻式压力传感器的实验标定结果进行了温度补偿。通过比较传统三次样条插值补偿后的传感器输出信号，验证了使用改进后的三次样条曲线插值法的补偿效果更好。这种方法为高精度压力传感器的温度补偿提供了一种有价值的理论依据。

传感器；温度补偿；三次样条曲线插值；非线性误差

硅压阻式压力传感器利用半导体材料的压阻效应来进行压力测量，以其体积小、灵敏度高、工艺成熟等优点，在各行业中得到了广泛应用。在实际工程应用中，由于半导体的温度特性导致压阻系数随温度变化，致使压力传感器的零点和灵敏度发生漂移，从而影响传感器的性能和测量准确度［1-2］。对于这一实际问题，通常采用在标准的温度、压力下测定传感器的特性，即传感器标定。基于标定实验结果，采取一定的方法进行修正，即软件修正。

目前的软件补偿方法主要采用曲线曲面拟合方法、神经网络方法和三次样条曲线插值的方法。也有不少学者根据长期的实践经验总结而来的多种补偿方法相结合的办法，如东南大学宋爱国教授提出的结合传统回归算法和遗传算法，在传感器的温度补偿中取得了良好的效果［3］。曲线曲面拟和精度不高，神经网络方法最大的缺点就是网络不稳定，训练时间较长［4］。三次样条曲线插值的方法是目前使用较为广泛的一种方法，因为三次样条插值由分段三次曲线连接而成，在连接点处二阶可导，具有良好的光滑性，能够准确反应传感器的真实特性［5］。但是在实际操作过程中，对于一些非线性误差较大的传感器，直接应用三次样条插值的办法并不能够达到很好的补偿效果。因此本文提出了一种基于三次样条曲线插值分别补偿零点、灵敏度和非线性误差的方法。并针对一种典型的硅压阻式压力传感器进行实际的处理和分析，其结果与直接应用三次样条插值的补偿结果进行比较。

1 三次样条曲线插值方法

当插值节点很多时，使用高次多项式插值并不能得到好的结果，因而一般采用分段插值法，即将插值区间分成若干个小区间，然后在每个小区间上使用次数较低的多项式进行插值。一般的分段插值法有一个严重的缺点，就是会导致插值函数在子区间的端点处不光滑，而三次样条曲线插值就不存在这个问题。三次样条插值由分段三次曲线连接而成，在连接点处有二阶连续导数，从而可以保证在连接点处光滑连接。

样条是绘图员用来描绘光滑曲线的一种简单工具［6］。设f（x）是［a，b］上的一个二次连续可微函数，在区间［a，b］上给定n+1个插值节点：a=x1＜x2＜…＜xn+1=b。设函数

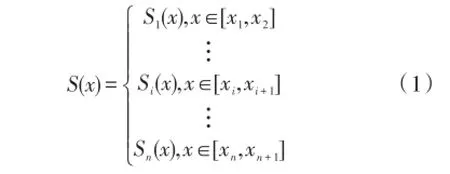
若S（x）满足条件

①S（x）在每个小区间［xi，xi+1］上是三次多项式，i=1，2，…，n+1

②S（x）在每个小区间［xi，xi+1］上具有连续二阶导数

则称S（x）是函数f（x）的三次样条插值函数。

设mi=S″（xi），hi=xi+1-xi，由三次样条的定义可知，S（x）的二阶导数在每一个子区间上［xi，xi+1］，i=1，2，…，n+1都是线性函数，于是在［xi，xi+1］上

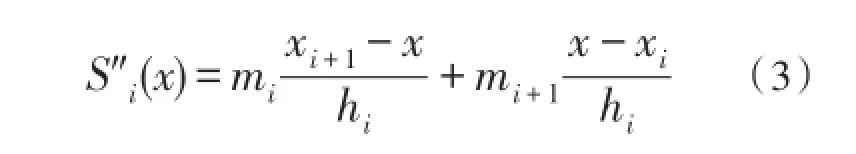
对式（3）连续积分两次

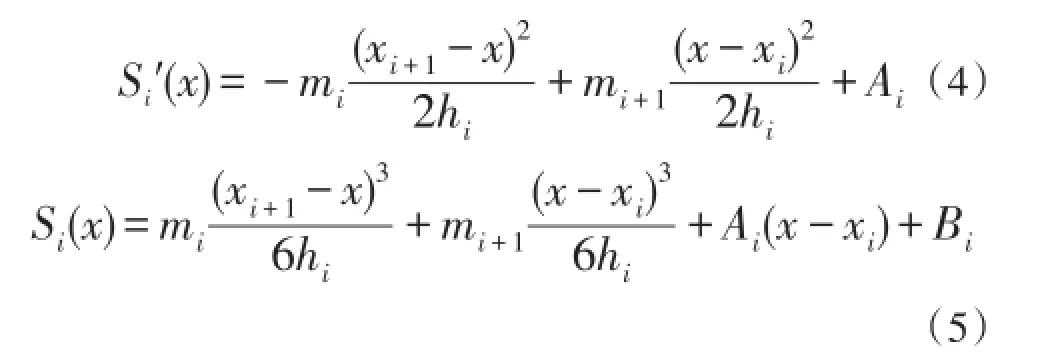
式中：Ai、Bi为积分常数，由式（1）、式（5）得

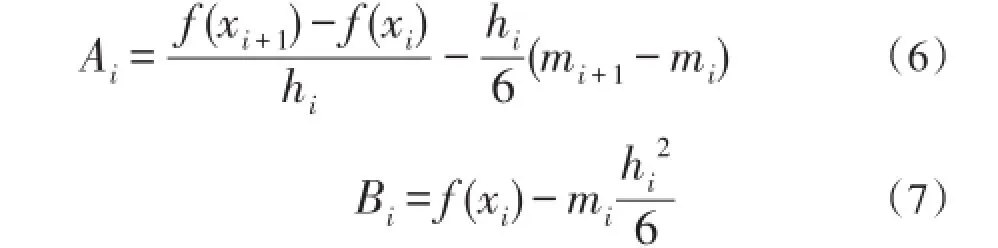
将式（6）代入式（4）得

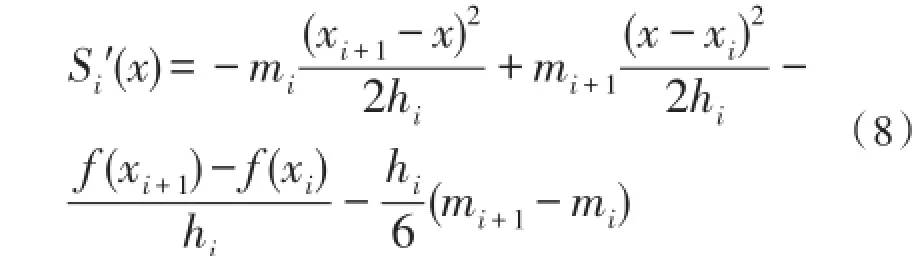
由于do连续，在［xi-1，xi］和［xi，xi+1］上的公共点xi处有相同值，即

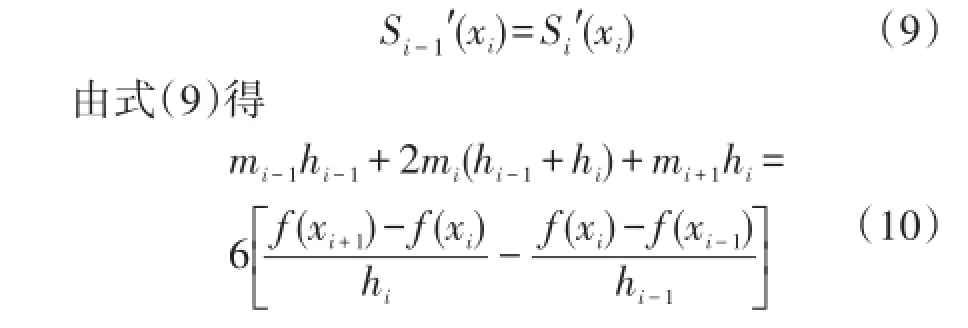
式（10）中i=2，3，…，n-1，结合边界条件

得到n-2个方程组，求得m1，m2，…，mn的值，从而得出三次样条插值函数S（x）［7］。传统的三次样条曲线插值法采用拟合标准压力、标准温度和传感器输出信号之间的插值函数，达到直接补偿的目的。

2 实验数据处理和分析

实验采用一款自制高精度仪表对传感器输出数据进行采集分析，仪表内部控制模块如图1所示［8-9］。

实验对象为BS10系列绝对压力传感器，因为是绝压传感器，其输出信号必定受到外部大气压力变化的影响，所以实验采用贝美克斯MC2气压校验仪对大气压力实时监控，MC2校验仪外置压力模块最小分辨率0.1 hPa，与数据采集仪表一致；标准压力源采用太航仪表的BQY-250气体活塞压力计；恒温恒湿高低温箱提供各种温度测试环境［10］。具体传感器温度补偿实验平台如图2所示。

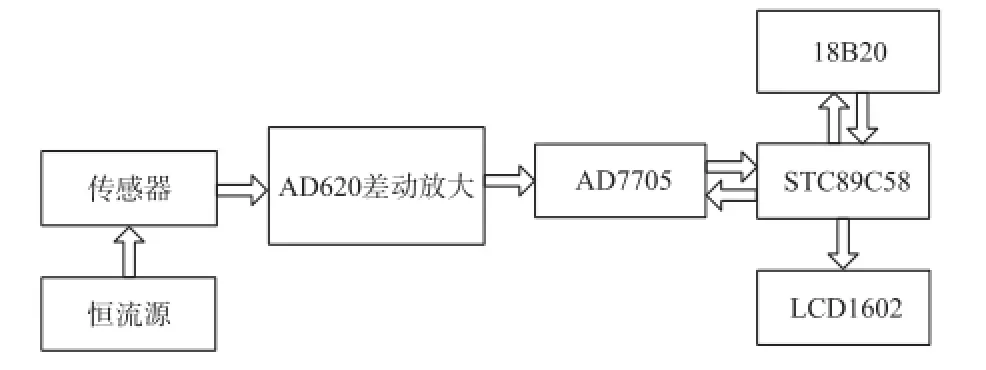
图1 仪表内部控制模块

图2 传感器温度补偿实验平台

测试时依次取温度点-20℃，-10℃，0℃，10℃，20℃，30℃，40℃，50℃，60℃。在每个温度点施加标准压力1 014.0 hPa，1 214.0 hPa，1 414.0 hPa，1 614.0 hPa，1 814.0 hPa，2 014.0 hPa，2 214.0 hPa，2 414.0 hPa，2 614.0 hPa，2 814.0 hPa，3 014.0 hPa，得到99个标定数值［11］，测得补偿前传感器输出数据如图3所示。

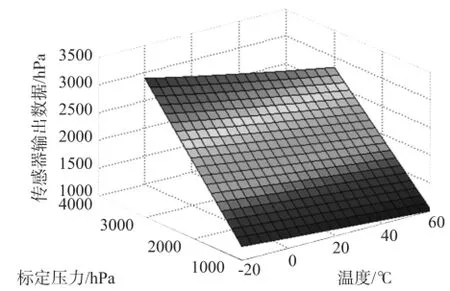
图3 补偿前传感器输出数据

传感器各温度点误差计算方法：

零点误差=零位标准值-零位输出

灵敏度误差=1-当前温度灵敏度=

由标定数据可得各个标定温度点的零点误差和灵敏度误差分布如表1所示。

表1 各温度点的误差分布

利用上面介绍的三次样条插值算法，根据标定数据将灵敏度误差对温度进行三次样条插值，将温度值代入插值曲线函数得到灵敏度误差量k，同理，将零点误差对温度进行三次样条插值得到温度相关的零点误差插值函数，代入温度值可以求出零点误差量b［12］。

经过灵敏度和零点补偿的传感器输出与实际标定数值还存在着不小的差距，这是由传感器的非线性决定的，全温度下各标定点的误差分布如表2所示：

误差值=传感器输出数值-标准压力值在温度固定的情况下将非线性误差值Fij（i=1，2，…，9，j=1，2，…，11）对标定压力P进行三次样条插值，得到9条被测压力和非线性误差的插值曲线，将传感器输出信号代入各温度点的插值曲线可以得到9个非线性误差值Fi。将这9个非线性误差值对温度Ti进行三次样条插值，得到非线性误差和温度的插值曲线。将温度值代入非线性误差和温度的插值曲线即可得到被测压力和当前温度下的非线性误差数值F［13］。

此时传感器的实际输出信号为：

式中：y为传感器输出数值，a0为传感器的零点输出a1为传感器的线性灵敏度，a2…an为传感器的非线性系数b为传感器的零点漂移，k为传感器的灵敏度漂移F为传感器的非线性误差补偿数值。

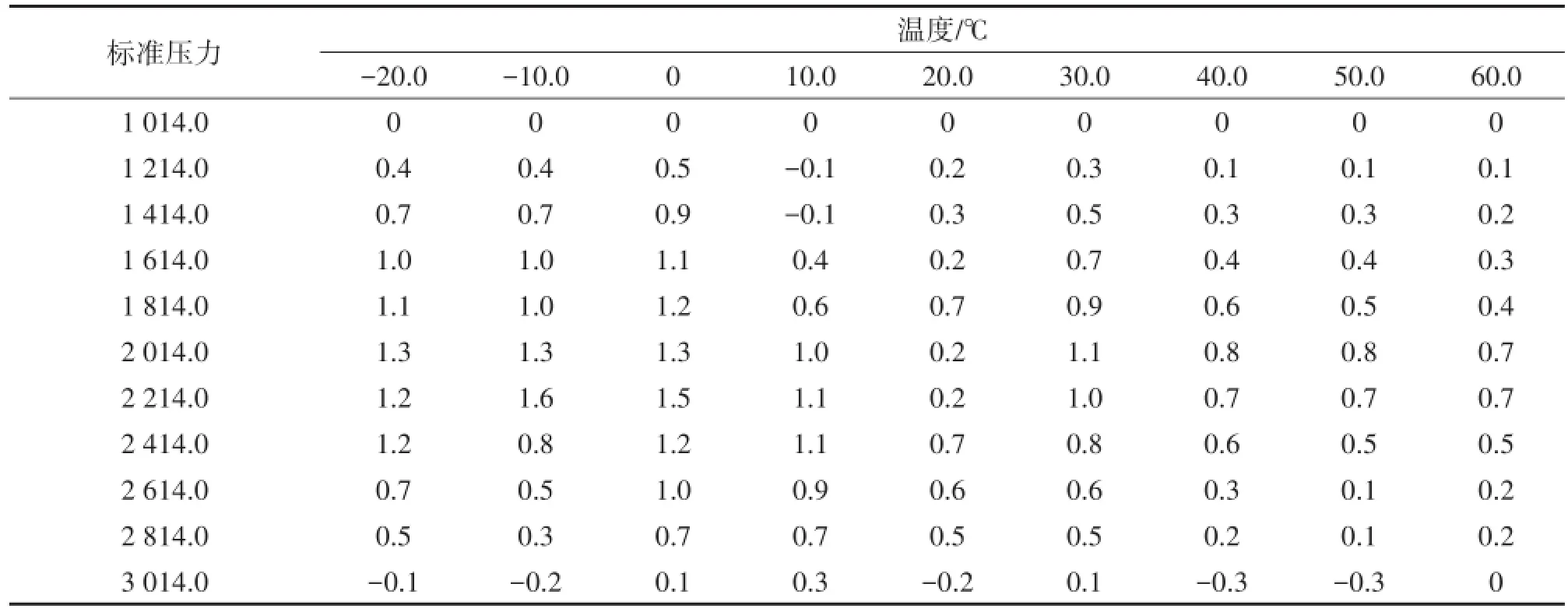
表2全温度下各标定点误差分布 单位：hPa

3 误差分析

对图1的传感器数据分别采用传统三次样条插值直接补偿和改进的三次样条插值分别补偿灵敏度、零点和非线性误差的方法，补偿后的传感器输出数值在插值节点处误差为零，为了正确检测传感器的误差分布，选取的检测点为各个插值节点的中间值［14］。得到的传感器输出数据减去标准压力获得两种方法补偿后的误差分布如4所示。

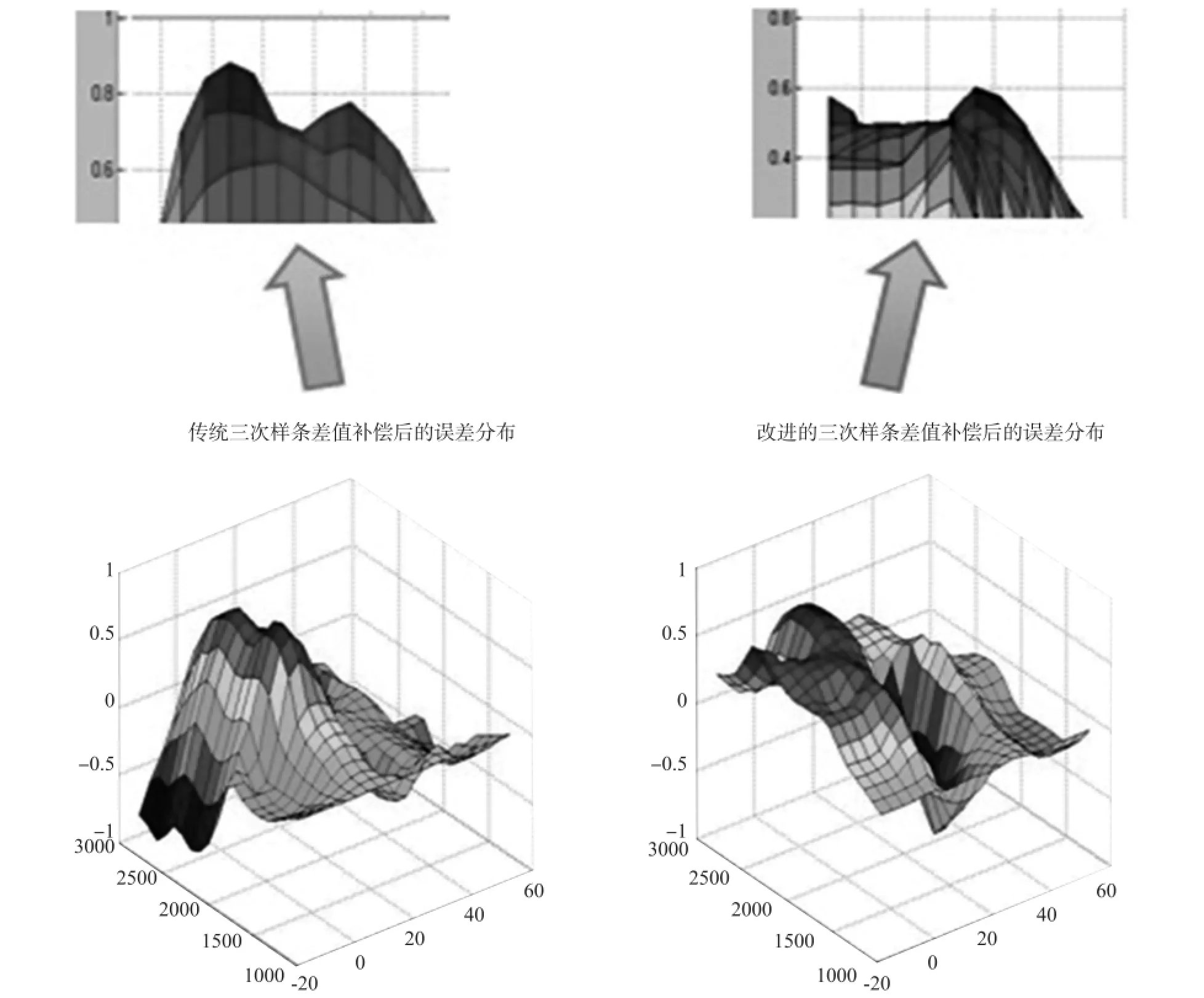
图4 两种补偿方法后的传感器误差分布（最高点放大）

综合误差是评定传感器性能优劣的一个综合指标，一般是由传感器的非线性和温度漂移引起的，可以用传感器在全温度范围内各标定点的输出值与理想值的最大偏移量与满量输出的百分比表示。

①采用传统三次样条曲线插值直接补偿传感器输出数据时，最大偏移量0.9 hPa，对应综合误差为0.045%。

②采用改进后的三次样条曲线插值分别补偿零点、灵敏度和非线性误差，最大偏移量0.6 hPa，对应综合误差为0.03%。

4 结论

本文提出的基于三次样条曲线插值的温度补偿方法，通过对零点、灵敏度和非线性误差的分别补偿，除了可以很大程度上减小传感器非线性对精度的影响，还可以降低信号调理电路和AD转换模块对系统精度的影响。使传感器输出信号不仅具有三次样条插值温度补偿的光滑性，而且比较直接应用三次样条插值曲线的方法补偿效果有所提高。特别是对于非线性误差的补偿方法，可以根据需要进行多次补偿计算，理论上能够进一步提高传感器精度。该方法对于其他的数据采集系统精度提升有一定的借鉴意义。

［1］ 孙以材，刘玉岭，孟庆浩.压力传感器的设计制造与应用［M］.北京：冶金工业出版社，2000：31-66.

［2］ Chen Shuang，Zhu Mingquan，Ma Binghe，et al.Design and Optimization of a Micro Piezoresistive Pressure Sensor［C］//IEEE International Conference on Nano/Micro Engineered and Molecular Systems，Nems，2008：351-356.

［3］ 陈晓颖，宋爱国，李建清.遗传算法在硅压阻气压传感器温度补偿中的应用［J］.测控技术，2010，29（增刊）：305-308.

［4］ 行鸿彦，彭基伟，吕文华.一种湿度传感器温度补偿的融合算法［J］.传感技术学报，2012，25（12）：1711-1716.

［5］ 李新.三次样条插值在称重仪表误差补偿中的应用［J］.电子设计工程，2011（11）：48-51.

［6］ 林成森.数值计算方法［M］.北京：科学出版社，1998：152-167.

［7］ Wang Xiaojia，Yang Shanlin.Dynamic GM（1，1）Model Based on Cubic Spline for Electricity Consumption Prediction in Smart Grid ［J］.China Communications，2010（10）：83-88.

［8］ 余剑锋，谭晓兰.硅微压阻式压力传感器的测试与研究［J］.山西电子技术，2013（2）：84-86.

［9］ 何伟铭，蒋超伟，井原透.高精度传感器标定曲线的预测拟合［J］.传感技术学报，2013，26（11）：1519-1524.

［10］ 胡园园，李淮江.基于ATmega16的压力传感器温度补偿智能化设计［J］.仪表技术与传感器，2010（10）：8-11.

［11］ 陶佰睿，顾丁，苗凤娟.一种基于单片机的湿度传感器校准实验平台设计与实现［J］.2013，26（3）：435-438.

［12］刘鹏.压阻式压力传感器温度补偿方法实现的研究［D］.天津：天津大学，2010：29-32.

［13］樊尚春，张秋利，秦杰.基于样条曲线插值的压力传感器的温度补偿［J］.北京航空航天大学学报，2006，32（6）：684-686.

［14］高磊，马英辉，刘祎.高精度硅压阻式气压计设计［J］.工矿自动化，2013，39（12）：21-25.

王冰冰（1989-），男，安徽淮北人，研究生，主要研究方向为智能传感器。2012 年9月～2013年7月在中国科学技术大学研究生课程班学习，2013年1月参加安徽省自然科学基金项目研究，第三参加人；

李淮江（1964-），男，安徽涡阳人，教授级高级工程师，硕士生导师。主要研究方向为智能传感器及无线传感网络。安徽省技术领军人才，安徽省“115”产业创新团队带头人，“检测技术及自动化装置”学科带头人。发表论文30余篇。获省部级科学技术奖5项，发明专利1项，承担省部级及教育厅科研项目12项。2004年底赴日本共和电业从事力敏传感器技术研修，2008年7月-2009年12月在香港理工大学任合作研究教授，从事织物传感器研究，msylhj@sina.com。

Temperature Compensation of Piezoresistive Pressure Sensor Based on the Interpolation of Third Order Splines*

WANG Bingbing，LI Huaijiang*
（Physics and Electronic Information College，Huaibei Normal University，Huaibei Anhui 235000，China）

The thermal zero drift，the thermal sensitivity drift and non-linear error of piezoresistive pressure sensor are the main factors of affecting the performance of sensors.So how to effectively compensate this kinds of errors to improve its performance is significative.The temperature compensation method based on the interpolation of third order splines was presented.The traditional compensation method based on the interpolation of third order splines was improved，to compensate zero drift，sensitivity drift and non-linear error respectively.This method was applied for the temperature compensation of the experimental results of piezoresistive pressure sensor.The measuring range of the pressure sensor is 1.014 0×105Pa～3.014 0×105Pa and the applied temperature range is-20℃～+60℃.By comparing the output signals by the sensor based on the traditional interpolation of third order splines，the effect about improved compensation method based on the interpolation of third order splines was better.The proposed method can provide a valuable theoretical reference for the temperature compensation of the high precision pressure sensors.

sensor；temperature compensation；third order splines；non-linear error EEACC：7230

TP2120

A

1004-1699（2015）07-1003-05

10.3969/j.issn.1004-1699.2015.07.011

项目来源：安徽省自然科学基金项目（1308085MF105）；安徽省国际科技合作计划项目（10080703003）；安徽省第七批“115”产业创新团队皖人才［2014］4号项目；安徽省高校自然科学研究重点项目（KJ2013A237）；安徽省校企合作实践基地项目（2012sjjd083）

2015-03-21 修改日期：2015-04-22