硅微电容式加速度计热致封装效应的层合分析*

周 铭，徐大诚，郭述文

（苏州大学微纳传感技术研究中心，江苏苏州 215100）

硅微电容式加速度计热致封装效应的层合分析*

周 铭，徐大诚*，郭述文

（苏州大学微纳传感技术研究中心，江苏苏州 215100）

由封装结构热失配引入的应力和结构变形会对MEMS器件性能产生显著影响，即热致封装效应。为描述该效应，一种基于缩减刚度矩阵的层合板模型被用来对硅微电容式加速度计的封装进行了建模。利用经典层合理论，由计算封装热失配引入的应变和曲率得到敏感检测电容的温度特性，以此作为热致封装效应的评估。并结合有限元模拟（FEM）对该理论模型进行了对比和验证。结果表明，层合模型能较好地描述硅微加速度计的热致封装效应，并在此基础上分析了优化措施。

MEMS；硅微加速度计；热致封装效应；层合板；缩减刚度矩阵

硅微电容式加速度计在封装过程中由于材料的热失配而引入的应力和变形对其性能和可靠性有着显著影响［1-2］。这种热应力在检测电容极板产生的弯曲直接影响了敏感电容的温度特性。对于此类问题，通常采用FEM模拟或实验观测的方法来计算和优化封装设计［3-9］，缺少相应的解析模型。相比数值计算，解析法能实现更快速的计算和优化［10-12］，并具备指导意义。时至今日，经典层合理论已广泛应用于多层板壳及复合材料的结构计算中［13］。硅微加速度计的封装多为多个薄层片的堆叠组合，其整体结构可视作层合板。本文在此基础上分析了硅微加速度计的热致封装效应，给出了层合模型，基于该模型的优化提出了封装改进措施。

1 层合理论

层合板是由两层或多层简单层板粘合在一起作为一个整体的结构单元。经典层合理论基于层间变形一致性假设和直法线不变假设，主要关注层合板沿厚度方向的应力和应变［13］。单层板是层合板分层的基本单元，其宏观力学特性是分析层合结构的基础。因此首先分析硅微加速度计封装模型的每一单层。如图1所示，传感器芯片经粘接剂粘贴至陶瓷基板，传感器芯片由硅衬底层、器件层和硅帽层组成。图2为该封装的层合板模型，共N（N=5）层，模型中各层均为各项同性材料，第k层材料杨氏模量Ek，泊松比νk，热膨胀系数（CTE）αk。

图1 硅微加速度计封装模型

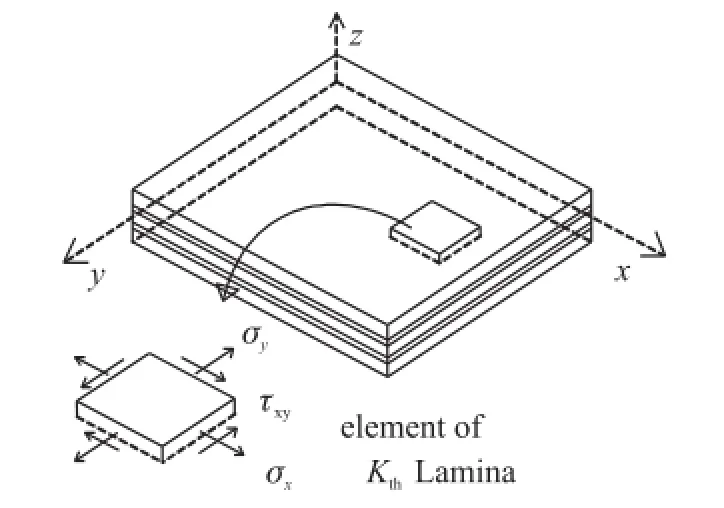
图2 封装的层合板模型

对每一单层板或壳，图2所示，依据平面应力状态假设—忽略厚度方向上的应力，其刚度矩阵［D］6x6可简化为缩减刚度矩阵［Q］3x3。经典层合理论给出了各项异性材料的缩减刚度矩阵形式。此处，基于封装模型中的材料均为各项同性材料，因此无需考虑材料坐标系与几何坐标系之间的转换［13］，第k层材料的缩减刚度矩阵［Q］k如（1）式：

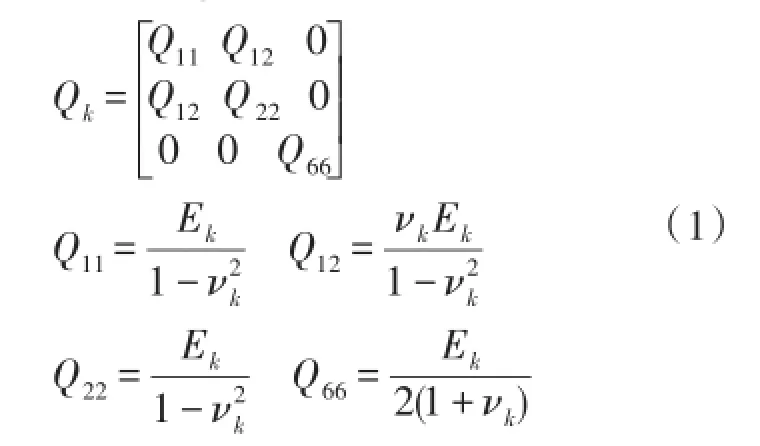
图3为层合模型的层坐标系示意图，各层堆叠次序如图所示，层1至层5分别为基板层、粘接剂层、硅衬底层、器件层（硅帽键合区域）和硅帽层。层1为氧化铝陶瓷基板、层2为环氧树脂胶（H70E），层3、层4、层5均为硅材料。第k层厚度为tk，层合板总厚度为t，中面位于z=0处，上、下表面分别位于±t/2处。各层的层坐标可按（2）式计算。可动质量块与与之相对的下电极组成变间距敏感电容。

基于层合理论，中面的弹性特征可用来表征整个层合板的弹性行为。忽略湿膨胀系数的影响，考虑热应力的内力和内力矩与层合板中面应变、曲率的本构方程如下［13］：

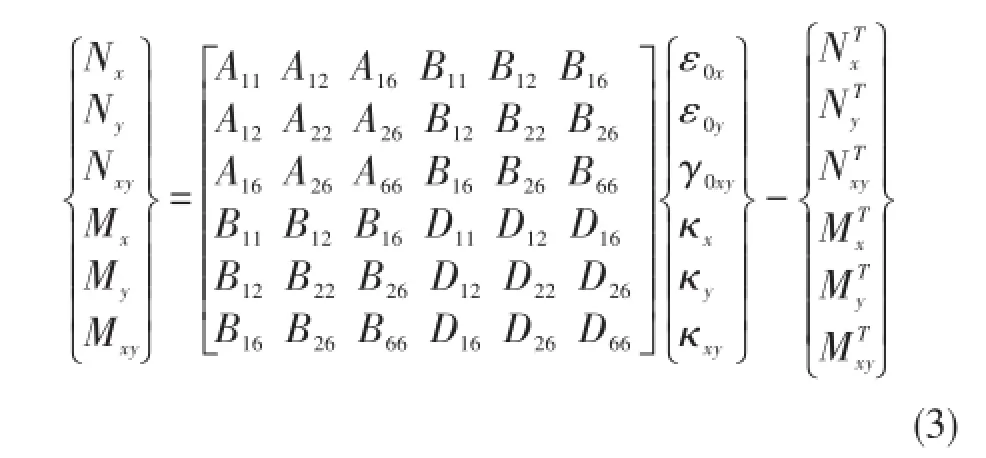
ε0x，ε0y，γ0xy，κx，κy，κxy分别为中面的应变和曲率。对称矩阵［A］为面内拉伸刚度矩阵，［B］为耦合刚度矩阵，［D］为弯曲刚度矩阵。其中：

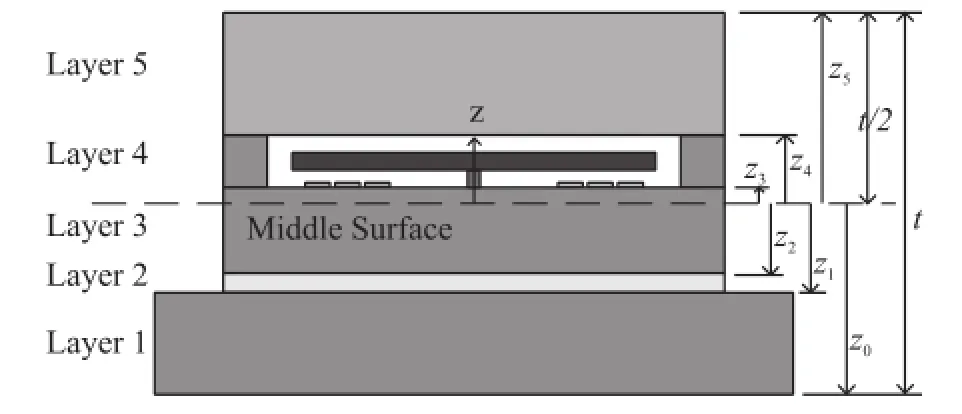
图3 层坐标系示意图

综上，热力和热力矩与层合板中面的应变和曲率之间的本构关系如式（6）：

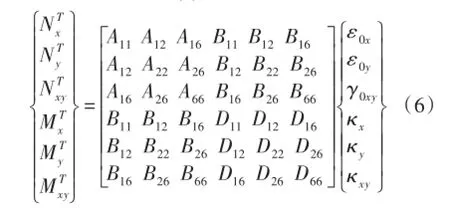
式中，［ABD］矩阵由式（1）、式（2）、式（4）计算得，其取决于层合板各层的厚度及材料特性；热力和热力矩由式（1）、式（2）、式（5）式计算得，取决于各层的厚度与材料特性、T0和ΔT。最后通过式（6）可得到层合模型中面的应变和曲率与温度T的关系。

此外，需对硅帽键合处的特殊结构作等效处理。如图3可知，层4与层5构成硅帽结构，但第四层结构不适用于经典层合板模型。文献［14］中给出了正交格栅结构［A］、［B］、［D］矩阵的等效形式，等效后的格栅结构可用于层合理论。硅帽的键合区域（层4）类似正交格栅结构，可类似地作一些近似等效：将格栅层（层4）的缩减刚度矩阵［Q］Grid按键合面积AGrid与整个芯片面积AChip的比值来重新定义。即：

2 应变和曲率对敏感电容的影响

借助由（6）式算得的中面应变和曲率可完全确定敏感检测电极的形变和弯曲，通过积分可得到敏感检测电容与温度T的关系。由于加工过程中引入的结构不对称在所难免，导致两差分检测电容的温度特性不完全一致，这直接影响了采用差分检测方式传感器的温度特性。此处通过计算单个敏感电容的温度特性来间接评估热致封装效应对传感器性能的影响。

粘接剂固化后，随着温度的变化，热应力使得层合板发生弯曲。如图4，加速度计的单支点质量块由于较小锚点的热应力隔离，其本身的弯曲可忽略，而与质量块对应的下层敏感电极与中面的弯曲特性一致。定义加速度计的平面内几何中心为XY平面的原点，T=T0时，质量块与敏感下电极的间距处处相等d=d0；T≠T0时，由于各项同性材料的层合模型关于x，y轴对称，曲率半径 ρx（T）=ρy（T）=ρ（T），故（x，y）处质量块与敏感下电极的间距：

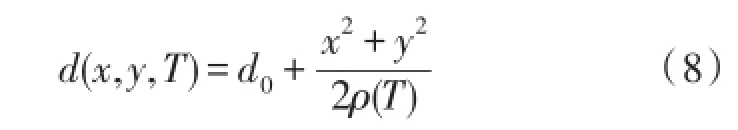
通过积分可得到下层敏感电极与质量块之间的静态电容C0（T）：

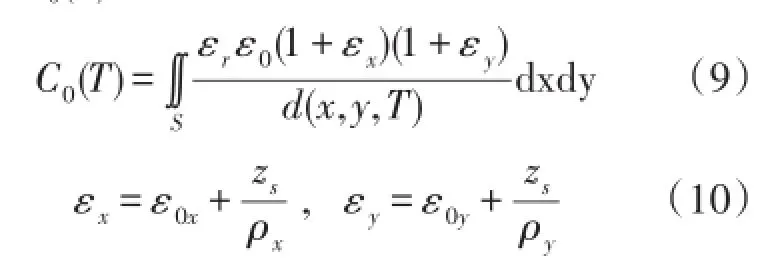
式中：εx，εy为敏感下电极区域S处的应变；ε0x、ε0y为中面应变；zs为敏感下电极在Z轴上的坐标值。

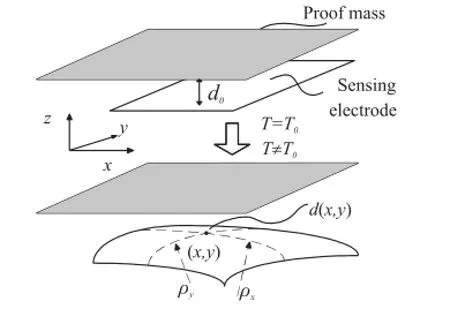
图4 质量块与敏感下电极的弯曲示意图（1/2模型）

3 热致封装效应的分析与优化

基于表1的材料属性，由式（6）可计算出表2中两种封装模型在不同温度下的曲率半径和静态电容值。此处，模型B中硅衬底（应力缓冲层）厚度较模型A中厚，环氧胶固化温度点T0定为150℃。

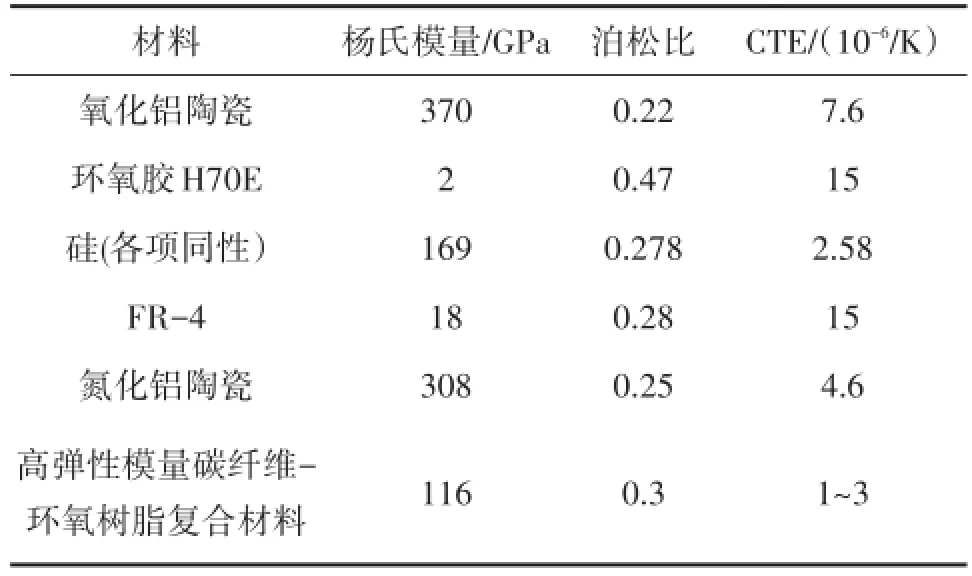
表1 封装模型材料属性

表2 封装模型各层的厚度参数 单位：μm

图5为层合模型计算的模型A和模型B中面的应变和曲率半径随温度的变化曲线。由式（8）和式（9），可计算得敏感电容的静态电容值变化量随温度的变化曲线，图6虚线所示。此处，相比电容间距变化对电容值的影响，εx和εy带来的面积变化对电容值的影响可忽略。利用ANSYS有限元仿真软件对图1模型进行热-结构分析，提取质量块和下层敏感电极的位移数据，经插值和数值积分同样可得到电容变化量与温度的关系曲线，图6实线所示。相比FEM值，层合模型的理论值稍偏大，偏差主要源自在各项同性材料中层合理论最理想的应用场合为长宽比为1、横向尺寸远大于纵向尺寸（厚度）的模型。图1所示模型长宽比偏离了1，实际上ρx（T）≠ρy（T）；其次实际模型与简化的层合模型存在一定差异。即便如此，理论值与FEM值依然大致吻合。对比模型A与B，增加应力缓冲层（硅衬底）的厚度改善了敏感电容的温度特性，层合模型和FEM模拟结果有着一致的趋势。

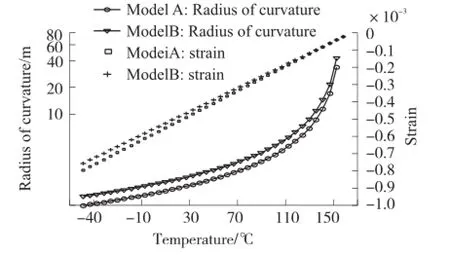
图5 模型A、B的应变和曲率半径与温度的关系

图6 单个敏感电容随温度的变化关系

相比FEM模拟，层合模型通过编程可实现快速计算和优化。层合模型中涵盖了堆叠层数、堆叠次序、温度、各层厚度和各层材料属性等优化对象，利用该模型可快速地对硅微电容式加速度计的封装设计提供定量的估算和定性的优化趋势。图7为以仅改变模型A中各层的厚度为例，室温时，由层合模型计算的各层的厚度对敏感电容的影响。图7（a）～7（c）分别为硅衬底层（层3）、硅帽层（层5）、粘接剂层（层2）厚度对敏感电容温度特性的影响。从计算结果可知：采用较厚的硅衬底、较厚的硅帽层或较厚的粘接剂层均可减小热致封装效应对器件的影响，其中以增加硅衬底层厚度对热致封装效应的改善最为明显。

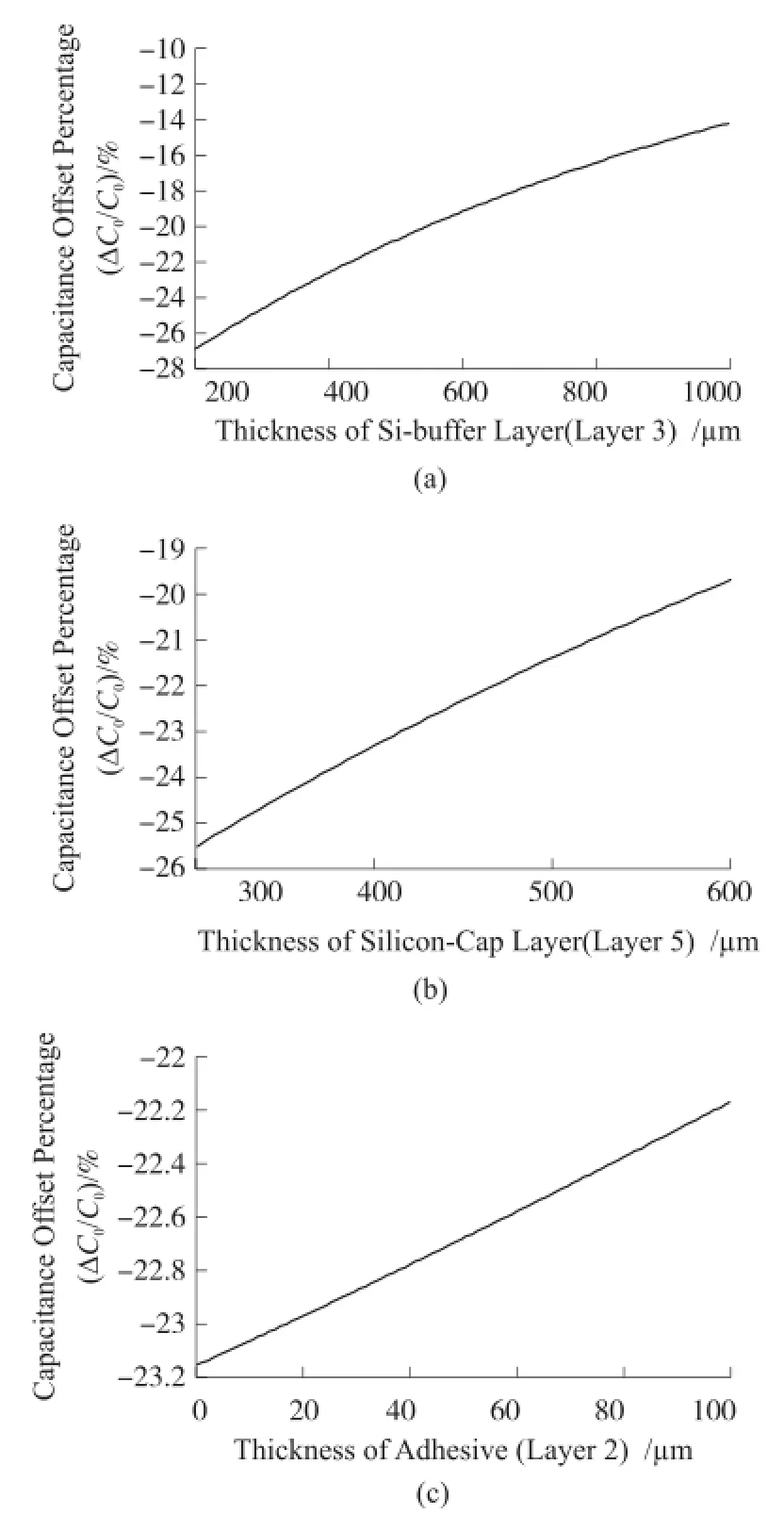
图7 模型A中硅衬底层、硅帽层、粘接剂层厚度对热致封装效应的影响

图8为基于模型A中各层的厚度，由层合模型算得的基板材料（见表1）对敏感电容温度特性的影响。可见，采用与硅材料CTE相近的材质的基板可显著改善热致封装效应，如氮化铝陶瓷基板、高弹性模量碳纤维-环氧树脂复合材料基板。

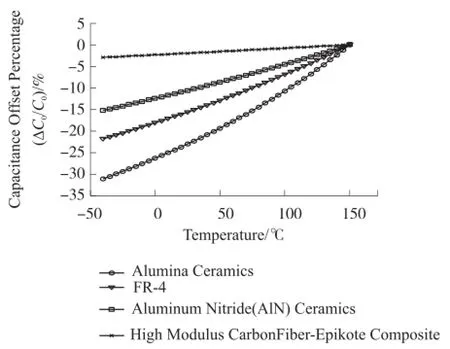
图8 基板材质对热致封装效应的影响（基于模型A中的厚度）

4 结论

本文利用基于缩减刚度矩阵的层合板理论，对硅微电容式加速度计的封装进行了建模分析。阐述了经典层合理论在热致封装效应分析中的应用。对硅帽中的类似格栅结构进行了近似等效。利用层合模型计算了两种封装模型的曲率和敏感电容随温度的变化关系，结合FEM模拟进行了对比验证，并在此基础上对封装模型的各层厚度和材料选取进行了优化分析计算。结果表明，层合模型较好地描述了硅微加速度计的热致封装效应，对封装设计的估算和优化具有一定的指导意义。

［1］ Krondorfer R H，Kim Y K.Packaging Effect on MEMS Pressure Sensor Performance［J］.IEEE Transactions on Components and Packaging Technologies，2007，30（2）：285-293.

［2］ Chou T L，Chu C H，Lin C T，et al.Sensitivity Analysis of Packaging Effect of Silicon-Based Piezoresistive Pressure Sensor［J］.Sensors and Actuators A：Physical，2009，152（1）：29-38.

［3］ Zhang Z，Wan Z，Liu C，et al.Effects of Adhesive Material on the Output Characteristics of Pressure Sensor［C］//2010 11th International Conference on Electronic Packaging Technology and High Density Packaging.2010：657-660.

［4］ 游侠飞，吴昌聚，郑阳明，等.基于有限元法的MEMS加速度计热应力分析［J］.传感技术学报，2012，25（2）：193-197.

［5］ Wang J，Yang L，Li X.On-Chip Integrated PS 3（Packaging-Stress Suppressed Suspension）for Thermal-Stress Fress Package of Pressure Sensors［C］//2013 IEEE 26th International Conference on Micro Electro Mechanical Systems（MEMS）.IEEE，2013：49-52.

［6］ 屈晓南，胡明，张世名，等.SiC高温电容压力传感器封装结构优化［J］.计算机仿真，2013，30（3）：92-96.

［7］ 向婷，郭涛，林大为，等.复合量程微加速度计封装热应力的研究［J］.仪表技术与传感器，2011（2）：9-11.

［8］ 李振，张国军，薛晨阳，等.MEMS仿生矢量水听器封装结构的设计与研究［J］.传感技术学报，2013，26（1）：25-30.

［9］ Zhang M，Du L，Zhao Z，et al.Low-Stress Packaging for a MEMS Atmosphere Pressure Sensor［C］//2013 8th IEEE International Conference on Nano/Micro Engineered and Molecular Systems （NEMS）IEEE，2013：665-668.

［10］宋竞，黄庆安，唐洁影.MEMS器件热致封装效应的解析建模研究［J］.传感技术学报，2006，19（）：1613-1616.

［11］Wen Y，Basaran C.An Analytical Model for Thermal Stress Analysis of Multi-Layered Microelectronic Packaging［J］.Mechanics of Materials，2004，36（4）：369-385.

［12］李敏，张加宏，刘清惓，等.非理想矩形锚单元的节点分析法［J］.传感技术学报，2013，26（5）：647-653.

［13］CAM Soares，CMM Soares，MJM Freitas.Mechanics of Composite Materials and Structures［M］.Springer Science and Business Media，1999.1-517

［14］Chen H J，Tsai S W.Analysis and Optimum Design of Composite Grid Structures［J］.Journal of Composite Materials，1996，30（4）：503-534.

周 铭（1988-），男，汉族，硕士研究生，主要研究方向为MEMS器件的结构设计与仿真，zmlove08@163.com；

郭述文（1955-），男，汉族，苏州大学电子信息学院特聘教授，主要研究方向为MEMS传感器设计与开发研究，shuwenguo@ wzxmems.com。

徐大诚（1963-），男，汉族，教授，主要研究方向为MEMS传感器信号处理技术研究，xudacheng@suda.edu.cn；

Analysis of Thermally Induced Packaging Effect of Silicon Micro-machined Accelerometer by Laminate Theory*

ZHOU Ming，XU Dacheng*，GUO Shuwen
（Micro/Nano Sensor Technology Research Center，Soochow University，Suzhou Jiangsu 215100，China）

Due to Structural stress and deformation from thermal mismatch，thermally-induced packaging effect on the performance and reliability of MEMS devices is significant.A laminate model based on reduced stiffness matrix is used for modeling the package of silicon micro-machined accelerometer to describe this effect.Through calculating the strain and curvature from thermal mismatch of the package by classical laminate theory，temperature characteristic of the sensing capacitor is obtained，which is used as the evaluation of thermally-induced packaging effect. Finally，results from comparison of FEM simulation and theoretical model show that laminate model can well describe the thermally-induced packaging effect of silicon micro-machined accelerometer，based on which，optimization of the package is also analyzed.

MEMS；silicon micro-machined accelerometer；thermally-induced packaging effect；laminate；reduced stiffness matrix

TN401；TN402

A

1004-1699（2015）07-0953-05

��0170J；2575

10.3969/j.issn.1004-1699.2015.07.002

项目来源：国家自然基金重点项目（61434003）

2015-01-19 修改日期：2015-03-14