Near continuum boundary layer flows at a flat plate

Chunpei Cai

Department of Mechanical and Aerospace Engineering，New Mexico State University，Las Cruces，NM 88003，USA

Near continuum boundary layer flows at a flat plate

Chunpei Cai

Department of Mechanical and Aerospace Engineering，New Mexico State University，Las Cruces，NM 88003，USA

a r t i c l e i n f o

Article history：

Received 17 December 2014

Accepted 25 December 2014

Available online 11 March 2015

Boundary layer

The problem of boundary layer flows at a flat plate surface with velocity-slip and temperature-jump boundary conditions is analyzed.With the velocity slip conditions，there are multiple physical factors lumpedtogether，andtheboundarylayersolutionssignificantlychangetheirbehaviors.Theself-similarity in the solutions degenerates，however，the problem is still an ordinary differential equation which can be solved.Shooting methods are applied to solve the flowfield.The results include velocity and temperature for both the surface and flowfield.Unlike the traditional Blasius flat plate boundary layer solutions which areself-similarthroughalltheplateboundarylayer，thenewsolutionsindicatethatthefronttipisactually a singularity point，especially at locations within one mean free path from the leading edge.

©2015 The Author.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http:// creativecommons.org/licenses/by-nc-nd/4.0/）.

The problem of incompressible boundary layer at a flat plate withnon-slipandconstantheatflux/temperaturewasinvestigated successfully.Blasius et al.［1，2］introduced a coordinate transformation method，and the governing Navier-Stokes partial differential equations（NSEs）for incompressible flows were transformed into a single ordinary differential equation，from which a universal velocity profile can be obtained for the whole flowfield.In addition，surface properties，such as the friction coefficients，are obtained theoretically.In the literature，there are many numerical and experimental studies as well.The solutions for boundary layer alongaflatplatewerederivedandtheycanfindmanyapplications，e.g.，crude estimations for drags over an airfoil.

As technologies and sciences advance，many new applications involvingboundarylayersemerge，andrarefication effectsmust be considered.For these flows，the traditional NSEs are not directly applicable.The rarefication effects are described by the Knudsen（Kn）number［3］

whereλisthemoleculemeanfreepath（MFP），andLthecharacteristic length.Larger Kn number flows can be created by large MFP（e.g.，in space engineering），or small characteristic lengths，e.g.，shock waves，gas flows inside micro-electro-mechanical systems/ nano-electro-mechanical system （MEMS/NEMS）.For example，Tretheway and Meinhart［4］reported in a micro-channel，with a very thin coating，the velocity slip can be quite apparent.Within the continuum flow regime（Kn＜ 0.001）with a small MFP，the NSEsapplywellwiththenon-slipvelocityboundaryconditions.As the Kn number continues to increase，flows change to the velocityslip and temperature-jump（0.001＜ Kn＜ 0.01）regime.With further larger MFPs，flows can be transitional（0.01＜ Kn＜ 10）and free molecular（10＜Kn）.Within the continuum flow regime，Blasius’s solutions are well developed；within the free molecular flow regime，the surface and flowfield solutions were obtained by Schaaf and Chambre［3］and Cai［5］.Within the transitional flow regime，we rely on numerical simulation methods.With the velocity slip and temperature jump regime，there has been some progress［6，7］，and the major goal of this paper aims to continue the discussions on flows within this regime.

The Blasius boundary layer on a flat plate with non-slip boundary conditions It is well known that for an incompressible gas flow over a flat plate，the NSEs can be simplified as

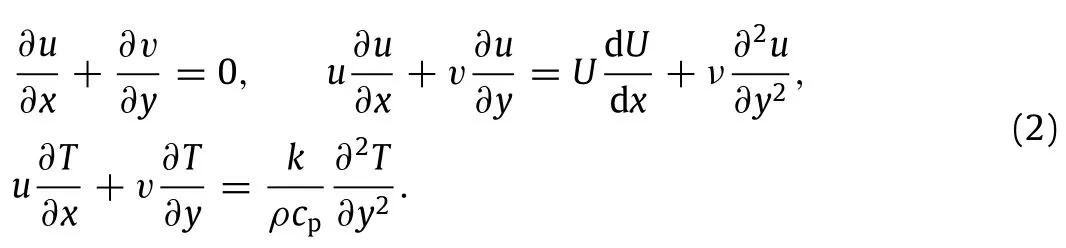
The plate surface conditions are listed as

The exact solutions to boundary layer flows over a flat plate were developed by Blasius，and were explained more conveniently by White［8］.A stream functionψ（x，η）can be adopted via a variabletransformation from（x，y）to（x，η）

whereνis the kinetic viscosity，and U the free stream velocity，f is a single variable function，The above new equation is a concise ordinary differential equation（ODE），not a partial differential equation（PDE）.As a result，there are exact solutions，and the solving procedure is simple.By using the shooting method［8］，the above two-point boundary value problem can be solved numerically.Some plate surface properties，such as friction coefficients，can be obtained analytically.

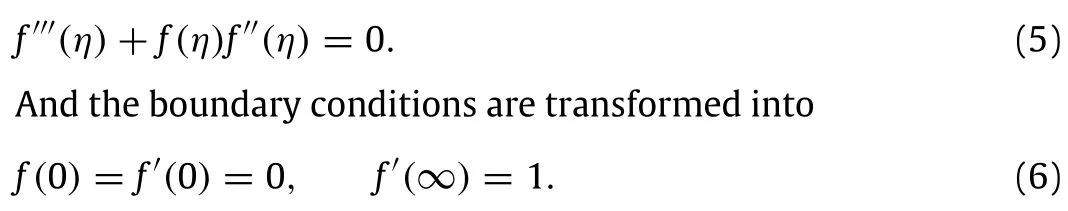
For the temperature field，with a transformation of variable［8］the governing equation and boundary conditions for temperature are

where Pr is the Prandtl number.The exact solution is

Slip velocity boundary conditions（0.001＜ Kn＜ 0.01）The previous section is the foundation for the work in this paper on velocity-slip and temperature jump boundary conditions.There is much related work in the literature，and they are reviewed as follows.

The first category of work concentrated on explanations of the velocity-slip and temperature-jump boundary conditions. Maxwell was the first one（1890）who discovered that due to the existence of the Knudsen layer close to the surface，the boundary condition at the plate surface shall have discontinuity effects，the velocity and temperature boundary conditions shall be modified［9，10］.Very soon，Smoluchowski［11，12］published two papers reporting similar results but with a separate method.Payne［13］relaxed Smoluchowski’s assumption，and provided more general results where a Maxwellian type boundary condition is merely a special scenario.By using the gaskinetic theory，and a multi-scale expansion method，Wu et al.［14］provided a slightly different，detailed explanation on the inner and outer solutions for flows in the velocity slip regime.It was emphasized by many researchers［15-17］，that when surface curvatures exist，then extra terms shall also be included in the velocity-slip boundary condition.Such past work concentrated on derivations for these velocity-slip boundary condition，rather than applying these new boundary conditions to the similarity solutions for boundary layer flows.Higher order slip boundary conditions［16］were also proposed.

A comprehensive review on experiments and numerical simulations of rarefied gas flows over a flat plate is available in the literature［18］.The non-equilibrium effects on the leading edge of a flat plate is reported［19］.Those work did not follow the approach for similarity solutions by Blasius.Recently，Matthews and Hill［20，21］discussed their work on slip flows over a flat plate with more general slip boundary conditions.In their work，no variable transformation was introduced，and the work did not include temperature jump boundary conditions.Martin and Boyd［6］reported their work on similarity solutions for flows over a flat plate with velocity-slip and temperature-jump conditions.They introduced an extra parameter K1which is related to x1/2，in addition to the two transformed variables（x，η）.

The velocity-slip boundary conditions can be expressed as

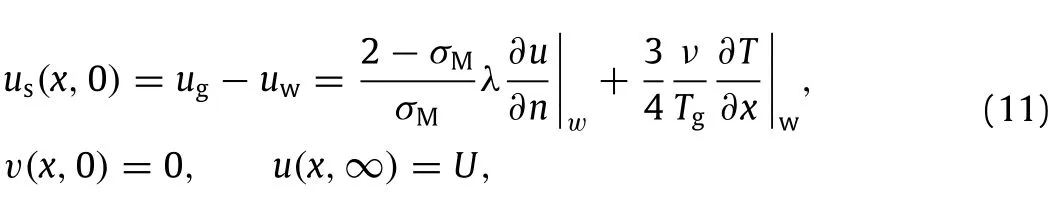
where usis the wall slip velocity，i.e.，the velocity difference between gas and the wall surface，ugthe gas bulk velocity adjacent to the wall，uwthe wall surface velocity，∂u/∂n the gas velocity gradient normal to the wall，σMa tangential momentum accommodation coefficient，Tgthe gas temperature，λthe MFP for a gas flow and can be described by the hard sphere modelfor a molecule of a diameter d，m the molecular mass，andρthe gas density which is usually of an ordinary value for gas flows inside MEMS.In general，the term containing temperature gradient in Eq.（11）is negligible when compared with the velocity gradient term.

With the same coordinate transformations，Eq.（4），the new velocity boundary condition changes

By using a crude gaskinetic estimation［22］

Eq.（12）can be transformed as

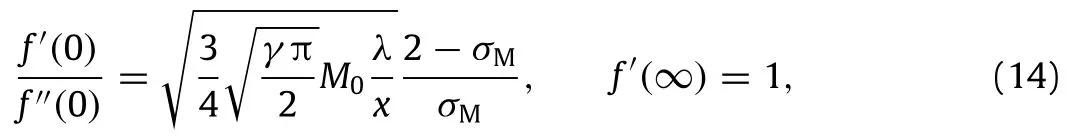
where the right hand side of the expression is defined as the slip coefficient，M0is the free-stream Mach number，andγthe specific heat ratio.Since several factors are combined together，it is evident that different changes of variables may achieve the same effect；for example，with a largerσM，or at a station x/λfurther downstream from the leading edge.Boundary conditions，Eq.（14），involve a normalized factor of x/λ.Hence，at different stations，the boundary conditions vary.Equations（5）and（14）are compatible，with the transformed coordinate system of（x，η）.The governing equation contains x implicitly throughη.Martin&Boyd［6］introduced an extra parameter K1which involves the Knxand Reynolds Rexnumber.The characteristic length for both is the distance from the leading edge，i.e.，x.As can be derived，K1∝KnxRe1/2x∝x−1/2，and it is improper to apply the derivative computation，due to the chain rule between the old coordinates（x，y）to the new coordinate system（x，η）Kumaran and Pop［23］investigated one related isothermal flow problem with a moving plate.Different from introducing a new parameter K1as Martin’s work，they performed a small parameter expansion method.Their approach is obviously improper because the slip coefficient which is defined in Eq.（14）includes a variable x which cannot be considered as a constant.

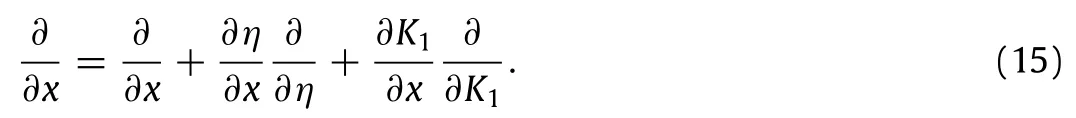
For gas flows inside MEMS/NEMS，or over a flat plate，the gas density is actually relatively constant；hence，the MFP does notchange much at room conditions.Due to this reason，a further introduction of Kn will not aid formulating the problem；the role of Kn number is minor and does not contribute much.The Re number is still crucial due to the inherited variable transformations.

For the temperature field，the boundary conditions are

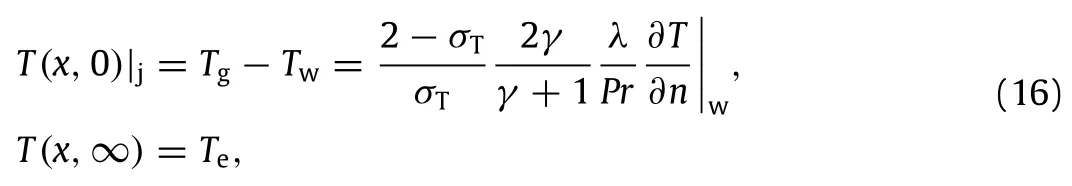
which can be transformed as，by using Eq.（13）and the definition ofηHere K0is a parameter which clearly displays all related factors，and if evaluated at a specific locationλ/x，then it can be treated as a constant.The work in this paper stillsolves Eq.（5）with the above new fixed boundary conditions，while Martin’s treatment actually alternate the governing equation and boundary conditions.

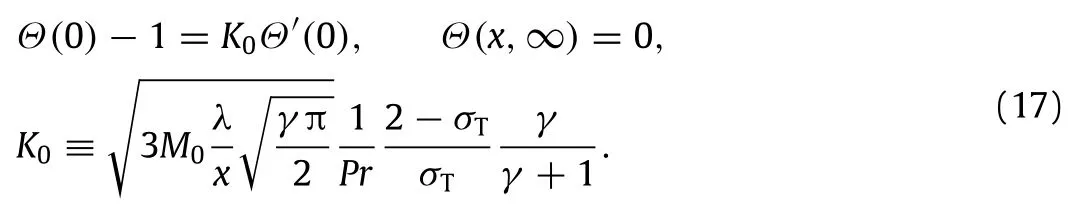
Equations（8）and（17）lead to the following exact solutions

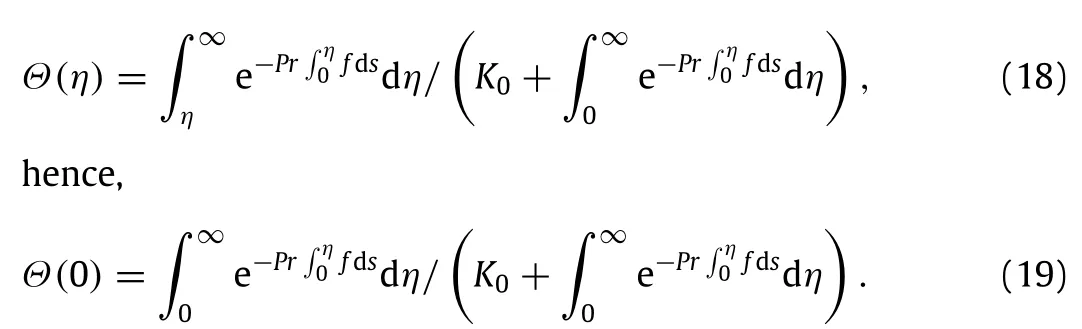
It is evident that properties at different stations x/λalong the plate surface，such as the gas temperature jumpΘ（0）can be computed with Eq.（19）.Further Eq.（17）leads toΘ′（0），which is related to the heat flux along the plate surface.

Discussions Equations（5）and（14）are in the transformed coordinate system of（x，η），and form one problem involving an ODE which can be solved numerically.For gas flows in MEMS，λ is relatively constant because the density is assumed to be almost constant.For the temperature solutions，they can be obtained from solutions of Eqs.（18）and（19）directly if the velocity solutions f（）are available.As can be understood，due to the introduction of the velocity slip condition，the self-similarity in the solutions degrades. Several factors and parameters，x/λ，γ，M0，andσu，are explicitly displayed，and a combination ofthem may lead to the same results.

A shooting method is adopted to solve Eqs.（5）and（14），by adjusting f′′（0）and f′（0）.Subsequently，the temperature and temperature gradient results are obtained without the shooting method.This section illustrates several results，and here the gas is assumed to be air withγ=1.4，and the free stream Mach number is set to 0.1 to satisfy the incompressible air flow assumption.

Severalvelocity profiles with different x/λvalues are illustrated in Fig.1.TheσMis set to 0.8.Further away from the plate leading point，flows behave more like incompressible with a non-slip velocity boundary condition，and the plate surface slip-velocity f′（0）decreases quickly.At the leading edge，the velocity changes significantly；essentially，the u-and v-components are of the same order，the flow is free molecular，and NSEs are not applicable.This is a well discussed topic with many papers in the literature［24］. Far from the leading edge，NSEs are applicable and the solution of f becomes more self-similar.This figure indicates that the solution at x/λ=102，or Knx=λ/x=0.01，is almost the same to the one at x/λ=106，or Knx=10−6.This is because Eqs.（14）and（17）degenerate to non-slip and constant temperature boundary conditions quite rapidly asλ/x→ 0.The velocity gradient profilesat different stations are presented in Fig.2.Asηincreases，the velocity profiles approach the outer stream value and the gradients decrease to zero at the edge of the boundary layer.Due to the existence of the velocity slip boundary condition，the flow reaches the free stream values faster than the corresponding results with the non-slip boundary conditions.For example，the boundary edge can be considered atη=5.0，while the non-slip one is atη=6.0. The gradients atthe surface converge rapidly fromthe leading edge point as well.Closer to the leading edge，the boundary layer thickness approaches to zero.

Fig.1.f′（η）at different stations，σM=0.8，M0=0.1，γ=1.4.

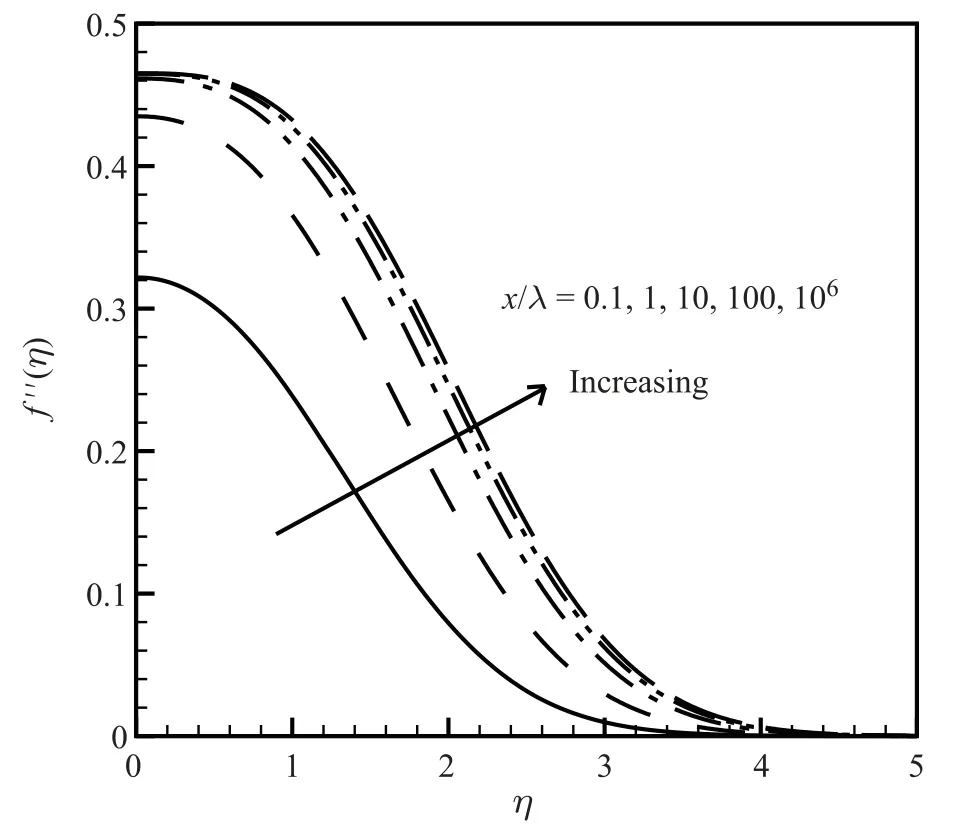
Fig.2.f′′（η）at different stations，σM=0.8，M0=0.1，γ=1.4.

Surface slip velocities due to differentσMare shown in Fig.3. The leading edge essentially is a singularity point with quite large slip velocities.AsσMincreases，the slip velocity decreases；this phenomenon indicates that largerσMresults in less rarefied gas flows.It is shown in Fig.4 that f′′（0）changes with a variation of σM.This property is closely related to the surface frictions Cf（x/λ），CD（x/λ），and normalized momentum displacement thickness θ（x/λ）/δ（x/λ）.Hereδ（x/λ）is a reference value from the non-slip boundary condition.WhenσMbecomes larger，those properties approach constant properties quickly.As illustrated in Fig.5，the surface boundary layer thickness，further away from the leading edge，continues to increase downstream-wisely.As the surface accommodation coefficient decreases，the boundary layer thicknessdecreases，and behaves more like the results from the non-slip boundary conditions.

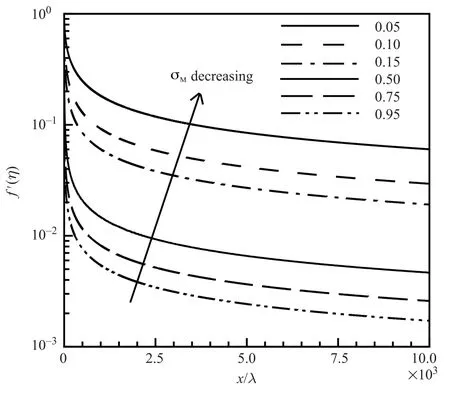
Fig.3.σMeffects on f′（0），M0=0.1，γ=1.4.

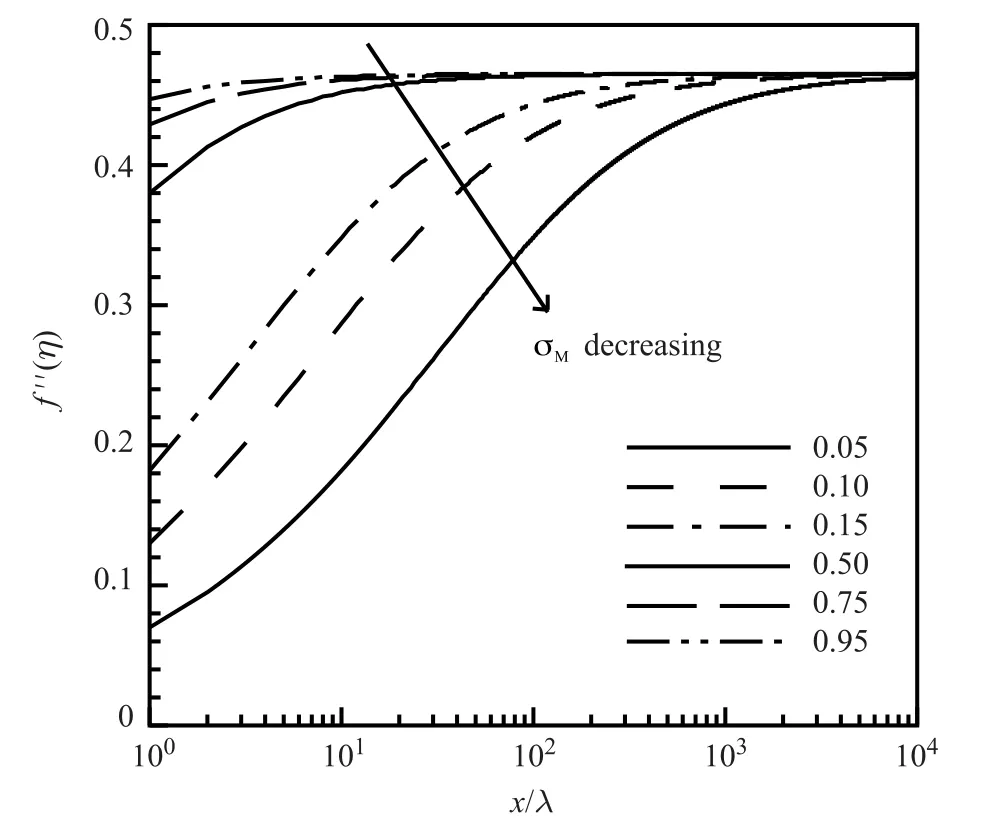
Fig.4.σMeffects on f′′（0）distributions，M0=0.1，γ=1.4.

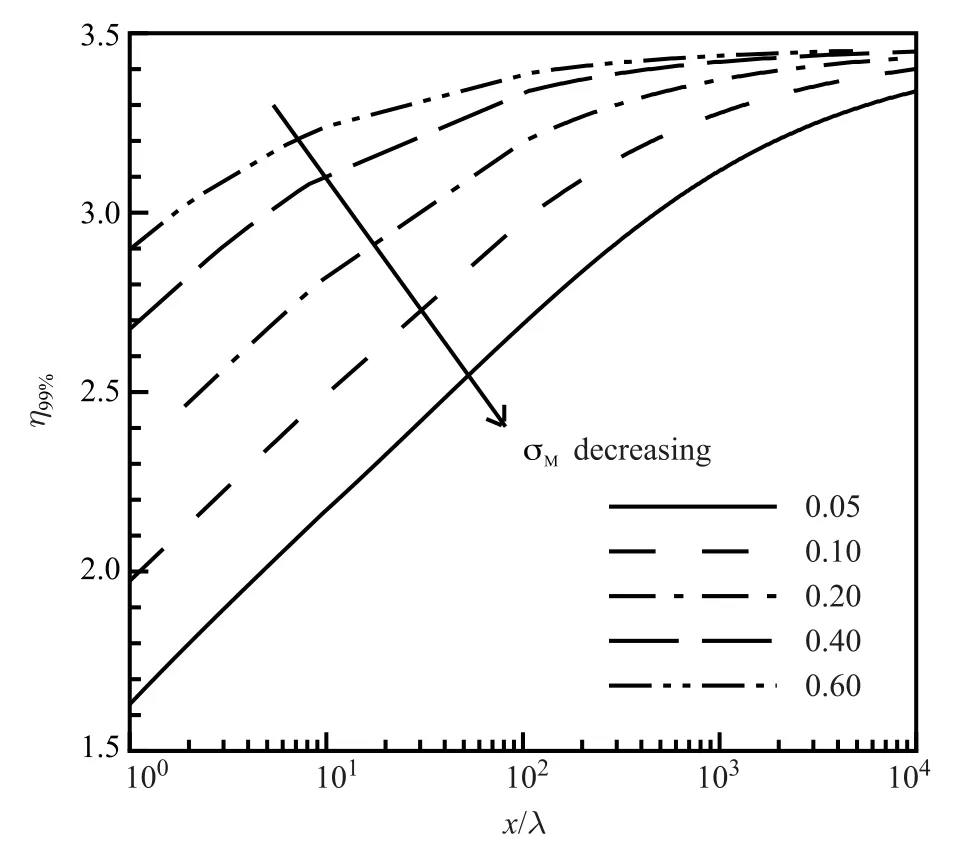
Fig.5.σMeffects on boundary layer thickness（specificηcorresponding to f′= 0.99）at different station x/λ.

Fig.6.DifferentσTeffects on thermal boundary layer profiles，σM=0.8，γ=1.4，Pr=0.72，M0=0.1，x/λ=104.

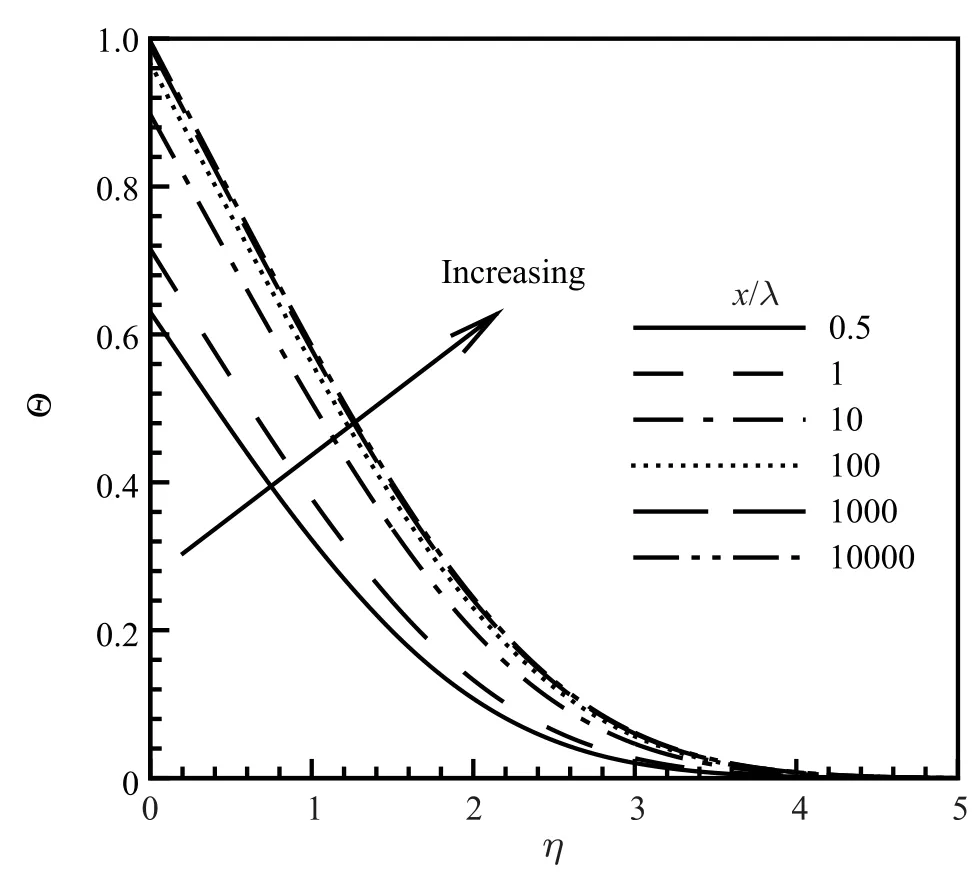
Fig.7.Temperature profiles at different stations，σM = σT=0.8，γ =1.4，Pr=0.72，M0=0.1.

The next two figures illustrate some properties related to the temperature jump.Equation（18）illustrates that exact solutions for the temperature distributions are closely related to the velocity profile f.Equation（17）indicates thatλ/x andσTprovide similar effects to the thermal boundary layer，as both are in the denominators.We can see in Fig.6 the thermal boundary layer profiles at a specific location x/λ=104，but with differentσT，which cannot create appreciable temperature differences.This indicates that at this specific condition，even with velocity slip and temperature jump boundary conditions，the flow is almost the same as the traditional none temperature jump Blasius boundary layer temperature distributions.Temperature profiles at different stations are shown in Fig.7.It illustrates that the temperature profiles change significantly from station x/λ=0.5 to station x/λ=20，or we can conclude that the traditional boundary layer solutions are recovered.These two figures clearly recovered the thermalboundary layer relation at the other region，Θ（∞）=0.

Figure 8 shows different surface temperatureΘ（0）at the plate surface under the effects of differentσT.The classical Blasiusboundary layer solutions shall provideΘ（0）=1 at the plate surface，and this figure clearly demonstrates that at locations further from the leading edge，this fact recovers.By using the relations between surface jump，Eq.（17），we can obtain the surface temperature gradientsΘ′（0）under the effects of differentσT.This relation linksΘ（x，0）andΘ′（x，0）；hence，they can be mapped from one to the other conveniently.The solutions for the temperature profiles are analytical；hence，no shooting method is needed.Instead，a simple integration of solved f（）shall be sufficient.Further，there are two sources which lead to different temperature results from this paper and those in the literature［6］.The first source is via different f（）which is inherited and explicitly included in Eqs.（18）and（19），and the second source is the new treatment in the temperature boundary condition，via Eq.（17）.

Table 1 Velocity slip boundary layer solutions f′′（0），γ=1.4，M0=0.1（the Blasius boundary layer solution［8］value is 0.4696）.

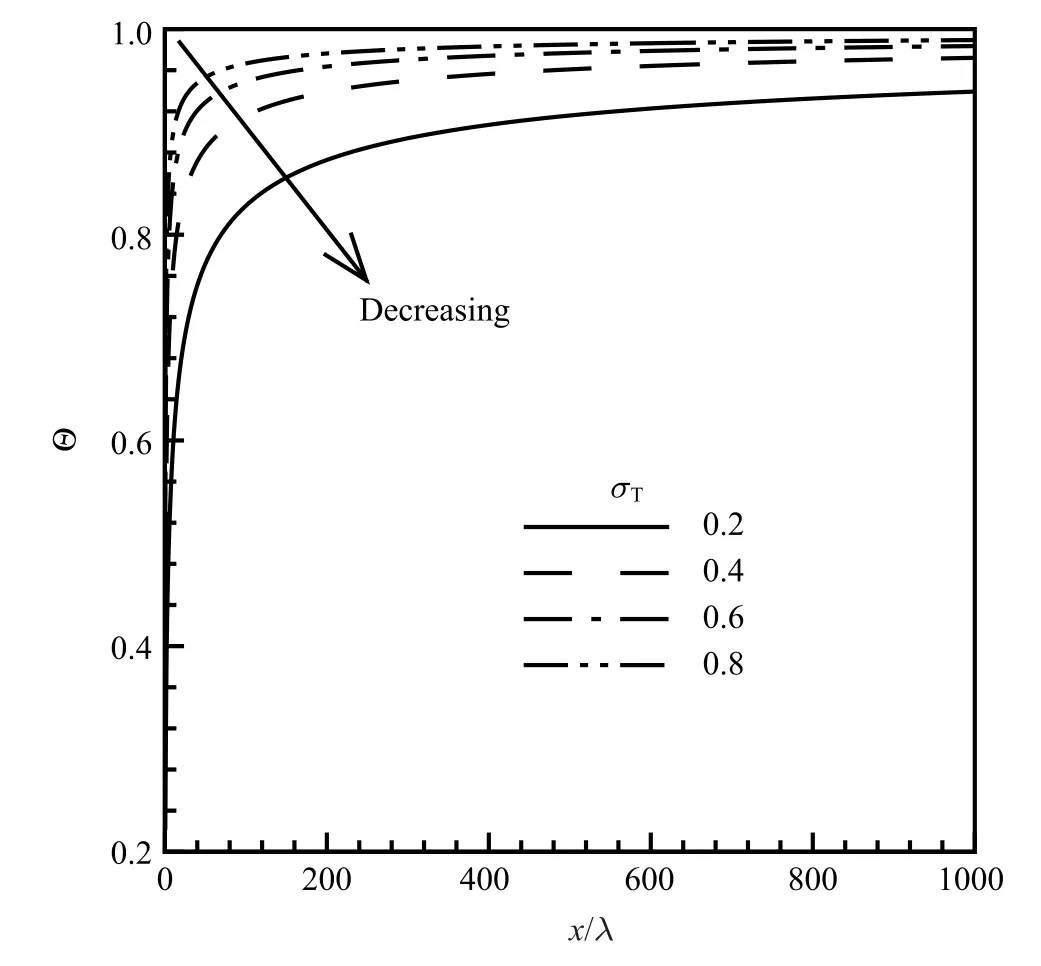
Fig.8.DifferentσTeffects on temperature profilesΘ（0）along plate surface，σM= 0.8，γ=1.4，Pr=0.72，M0=0.1.

It is well known that the Blasius boundary layer solutions are not valid at the leading edge，especially within a distance of one mean free path.One of several reasons for this is the velocity components u and v are of the same orders；hence，one important assumption to simplify the Navier-Stokes equations becomes invalid.However，the current solutions partially alleviated the problembecause rarefication effects are achieved by adding rarefication effect through the boundary conditions，as such，it can be expected thatthe analyticalsolutions in this work is more general.However，to validate the solutions is rather challenging because both numerically and experimentally we have difficulties in probing into regions of one mean free path.For numerical simulations，high resolutions require fine grids；for experiments，the diameter of a hot wire can be easily larger than one mean free path.Validating the results may demand long term effort；at this stage，we can examine whether downstream-wise these carefully derived solutions can degenerate to incompressible boundary layer solutions. Table 1 demonstrates thatconvergence to the traditionalboundary layersolutions is evident.The K0parameterin Eq.（17）predicts that increasing x/λwithσTunchanged can achieve similar effects as increasingσTwith x/λunchanged，and this table confirms this prediction.

Atthe end ofthis section，the majordifferences among this work and those in other two recent papers［6，25］are emphasized as follows.The work in these three papers concentrated on the Blasius boundary layer problems with the velocity-slip boundary conditions；hence，they are in the same vein.Martin［6］introduced a new parameter K1as one extra variable.Actually by doing that，the governing equation for the velocity profile changes from a singlevariable function f（η）to a new two-variable function f（η，K1），and according to the chain rule for derivatives，a correctfinalgoverning equation shall be a partial differential equation.This work and that by Aziz［25］are quite close，both still concentrate on the ordinary differentialequation，neither introduce such an extra parameter K1as Martin proposed.This work further demonstrates that many exact physical factors can be combined into an explicit factor K0.Aziz assumed a constant heat flux at the plate surface with∂T/∂n= constant；while this work solved the temperature jump condition，Eq.（17），and an explicit temperature profile solution，Eq.（18），is obtained in this work.This new solution illustrates strong connections between the temperature and velocity profiles.

Summary Boundary layers at a flat plate with a velocity-slip and temperature-jump surface conditions are analyzed.The velocity profiles can be solved as an ODE，and the results are different from the previous ones in the literature.Even though the general similarity properties are lost due to the new boundary conditions，the problemcan be solved relatively easier than a PDE.With the velocity profiles obtained，the corresponding temperature distributions can be obtained by integrations numerically without a need of the shooting method，and the results are different from the previous ones in the literature，because the involved velocity profiles are different.Detailed parameters from the boundaries are listed separately，and their impacts can be monitored parameter by parameter.

［1］H.Blasius，Grezschichten in flüssikeiten Mit kleiner reibung，Z.Angew.Math. Phys.56（1908）1534-1535（in German）.

［2］H.Schlichting，K.Gersten，Boundary Layer Theory，second ed.，McGraw-Hill，Columbus，1962.

［3］S.A.Schaaf，P.L.Chambre，Flow ofRarefied Gas，Princeton University Press，New Jersey，1961.

［4］D.C.Tretheway，C.D.Meinhart，Apparent fluid slip at hydrophobic microchannel walls，Phys.Fluids 14（2001）L9.

［5］C.Cai，Free-molecular gas flow over a flat plate，in:Proceedings of the 29th International Symposium on Rarefied Gasdynamics，Xi’an，July，2014，China.

［6］M.Martin，I.D.Boyd，Momentumand heattransferin a laminar boundary layer with slip velocity，J.Thermophys.Heat Transfer 20（2006）710-719.

［7］M.H.Yazdi，S.Abdullah，I.Hashim，A.Zaharim，K.Sopian，Friction and heat transfer in slip flow boundary layer at constant heat flux boundary conditions，Math.Comput.Sci.Eng.（2008）207-212.

［8］F.White，Viscous Fluid Flow，first ed.，McGraw-Hill，New York，1991.

［9］E.H.Kennard，Kinetic Theory of Gases，McGraw-Hill，New York，1939.

［10］M.N.Kogan，Rarefied Gas Dynamics，Plenum Press，New York，1969，pp.386-400.

［11］M.V.Smoluchowski，Sitz.ber.，Oesterr.Akad.Wiss.Math.-Nat.wiss.Kl.II 107（1898）304.

［12］M.V.Smoluchowski，Sitz.ber.，Oesterr.Akad.Wiss.Math.-Nat.wiss.Kl.II 108（1899）5.

［13］H.Payne，Temperature jump and velocity slip at the boundary of a gas，J.Chem.Phys.21（1953）2127，http://dx.doi.org/10.1063/1.1698798.

［14］Q.F.Wu，W.F.Chen，L.Huang，Y.Z.Shi，Rarefied Gasdynamics（in Chinese），National Defense University Press，2004.

［15］X.Chen，Gasdynamics and Its Application in Heat Transfer and Gas Flows（in Chinese），Tsinghua University Press，Beijing，1996.

［16］D.A.Lockerby，J.M.Reese，D.R.Emerson，R.W.Barber，The velocity boundary condition at solid walls in rarefied gas calculations，Phys.Rev.E.70（2004）017303.

［17］X.Sun，R.W.Barber，D.R.Emerson，The impact of accommodation coefficient on concentric Couette flow，in:24th International Symposium on Rarefied Gasdynamics，Bari，Italy，2004.

［18］J.L.Potter，The transitional rarefied flow regime，in:Proceedings of 5th International Symposium on Rarefied Gasdynamics，vol II，Academic Press，1967.

［19］J.A.Laurmann，Structure ofthe boundary layeratthe leading edge ofa flatplate in hypersonic slip flow，AIAA J.2（1964）1655-1657.

［20］M.T.Matthews，J.M.Hill，Nano boundary layer equation with nonlinear Navier boundary condition，J.Math.Anal.Appl.333（2006）381-400.

［21］M.T.Matthews，J.M.Hill，A note on the boundary layer equations with linear slip boundary condition，Appl.Math.Lett.21（2008）810-813.

［22］W.G.Vincenti，C.H.Kruger，An Introduction to Physical Gasdynamics，first ed.，John Wiley and Sons，New Jersey，1965.

［23］V.Kumaran，I.Pop，Nearly parallel Blasius flow with slip，Commun.Nonlinear Sci.16（2011）4614-4619.

［24］J.Morito，R.Street，The incipient continuum flow near the leading edge of a flat plate，in:Proceedings of The 4th International Symposium on Rarefied Gasdynamics，July，Toronto，Canada，1965，pp.416-432.

［25］A.Aziz，Hydrodynamic and thermal slip flow boundary layers over a flat plate with constantheatflux boundary condition，Commun.Nonlinear Sci.15（2010）573.

E-mail address：ccai@nmsu.edu.

http://dx.doi.org/10.1016/j.taml.2015.03.005

2095-0349/©2015 The Author.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

Rarefication

Slip flows

*This article belongs to the Fluid Mechanics