Transition and self-sustained turbulence in dilute suspensions of finite-size particles

I.Lshgri∗，F.Picnob，L.Brndt

aLinné FLOW Centre and SeRC，KTH Mechanics，Stockholm，Sweden

bIndustrial Engineering Department，University of Padova，Padova，Italy

Transition and self-sustained turbulence in dilute suspensions of finite-size particles

I.Lashgaria，∗，F.Picanoa，b，L.Brandta

aLinné FLOW Centre and SeRC，KTH Mechanics，Stockholm，Sweden

bIndustrial Engineering Department，University of Padova，Padova，Italy

a r t i c l e i n f o

Article history：

Received 8 December 2014

Accepted 22 January 2015

Available online 24 April 2015

Flow transition

Suspension

Finite-size particles

Lift-up effect

We study the transition to turbulence of channel flow of finite-size particle suspensions at low volume fraction，i.e.，Φ ≈ 0.001.The critical Reynolds number above which turbulence is sustained reduces to Re≈1675，in the presence of few particles，independently of the initial condition，a value lower than that of the corresponding single-phase flow，i.e.，Re≈1775.In the dilute suspension，the initial arrangement of the particles is important to trigger the transition at a fixed Reynolds number and particle volume fraction.As in single phase flows，streamwise elongated disturbances are initially induced in the flow. If particles can induce oblique disturbances with high enough energy within a certain time，the streaks breakdown，flow experiences the transition to turbulence and the particle trajectories become chaotic. Otherwise，the streaks decay in time and the particles immigrate towards the channel core in a laminar flow.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

Understanding the characteristics of suspension flows is of fundamental and practical importance in natural phenomena，e.g.particles in the atmosphere and water，and industry，e.g.transportation and mixing.The focus of this paper is therefore on the transition from the laminar to the turbulent flow of dilute suspensions of finite-size particles，particles larger than the smallest flow scales，a process associated to a significant（usually sudden）alteration of the nature of the flow.Although the dynamics is governed by a single non-dimensionalparameter—the Reynolds number，the ratio ofinertia to viscous forces，transition ofsingle phase flows has challenged the scientists fora long time and itis notyetcompletely understood.The behavior of suspensions is more complicated because ofthe various particle properties such as size，number，shape，deformability，density.

To the best of our knowledge，there exist only few studies of the transition to turbulence of suspensions of finite-size particles（for the case of point particles the reader is referred to Ref.［1］and references therein）.The experiments by Matas et al.［2］examine the effects of finite-size neutrally buoyant particles on the transition in pipe flow.These authors report that suspensions of large particles exhibita non-monotonic behavior ofthe criticalReynolds number when increasing the particle volume fraction.The different regimes are identified by the pressure drop between the inlet and outlet of the pipe.A decade later and thanks to the improvement of computational algorithms and resources，numerical simulations of finite-size particle suspensions start to emerge.Yu et al.［3］partially simulate the experiments in Ref.［2］.Since the flow is always perturbed by the presence of the particles，the level of streamwise velocity fluctuations is used to define a threshold to distinguish between laminarand turbulentflow.The experimental behavior in Ref.［2］could be reproduced by tuning this threshold parameter，showing the difficulties to define the transition threshold in suspensions.A more detailed analysis ofthe flow in the transitional regime is reported by Loisel et al.［4］where a fixed particle volume fraction is examined，Φ≈5%.These authors show that the coherentstructures ofthe flow are broken by the presence offinite size particles and smallereddies（more energetic）prevents the flow from relaminarization when decreasing the Reynolds number；this effect promotes therefore turbulence.

Summarizing，transition delay is attributed to the enhancement of the effective viscosity of the suspensions for smaller particles［2］，whereas promotion of transition is，instead，qualitatively attributed to large disturbances induced by particles of large enough size.

Recently Lashgari et al.［5］studied suspensions of spherical neutrally buoyant particles for a wide range of Reynolds numbers，Re，and box-averaged volume fractions，Φ.These authors examinethe globalmomentum balance［6］and reportthe existence ofthree different regimes when varyingΦand Re.For lowΦand Re，the flow is laminar and the viscous stress dominates.For high Re and sufficiently lowΦ，the flow is turbulent and the Reynolds stress contributes the most to the momentum transport as in classic single-phase turbulence.The flow is dominated by the particle stress at moderateΦ.

For the cases at lowΦ，transition is sharp when increasing the Reynolds number and can be easily identified，e.g.by the level of fluctuations and wall shear stress；at highΦ，however，all the observables vary smoothly with Re.The latter case is denoted as inertial shear-thickening since it is characterized by a significant increase of the wall friction that is not attributed to an increase of the Reynolds stress butto the enhancementofthe particle-induced stress.

The aim of this letter is to examine the reduction of the critical Reynolds number above which turbulence exists in very dilute suspensions offinite size particles.We study in details the mechanism behind the transition promotion and relate this to self-sustained turbulence by analyzing the kinetic energy induced by the particles and transferred from small scales to large scales.

We perform direct numerical simulation of suspensions laden with rigid spherical neutrally buoyant particles.We employ an immersed boundary solver based on the original formulation by Uhlmann［7］and developed by Breugem ［8］.The code couples a fixed uniform Eulerian mesh for the fluid phase with a quasiuniform Lagrangian mesh representing the surface of the particles. The fluid velocity is interpolated on the Lagrangian grids，the immersed boundary forcing is computed based on the difference between the particle velocity and the interpolated fluid velocity at each Lagrangian grid point and finally the forcing spread out from the Lagrangian to the Eulerian mesh.The near field interactions are treated by means of lubrication forces and soft-sphere collision models.The code has been validated against several test cases in Refs.［5，8］.

We simulate the flow in a pressure-driven channel flow with streamwise and spanwise periodic boundary condition and no slip condition at the walls.The box size is 2h×3h×6h in the wallnormal，spanwise，and streamwise directions where h is the half channel height.The domain is larger than the minimal unit channels used for transition in Newtonian fluids［9］and polymer suspensions［10］.The numberofEulerian grid points is 160×240×480 with 746 Lagrangian points used to resolve the surface of each particle.The ratio between the channel height and particle diameters is fixed to 10（with 16 grid points per particle diameter）.The particle diameter is that pertaining the case in the experiment［2］where the strongest non-monotonic behavior of the critical transition threshold is observed.We denote streamwise coordinate and velocity by v and y，wall normal by w and z，and spanwise by x and u.The simulations are performed imposing a constant mass flux，with the bulk velocity denoted by Ub.The Reynolds number is defined as Re=2Ubh/νwhereνis the fluid kinematic viscosity.In order to calculate the characteristics of the two-phase flow，a phase field indicator（mask），ξ，is created for the total field such thatξ=1 indicates the solid phase andξ=0 the fluid phase. The parameters ofthe fluid phase，e.g.rootmean squared（rms）velocities，are then obtained by taking average over all the Eulerian points withξ=0 and similar for the particle phase withξ=1.

In this work，we study the transition and self-sustained turbulence in a channel flow laden with few finite-size neutrallybuoyant particles（dilute regime）and compare the results with the one ofthe single-phase（Newtonian）flow.We use only 10 particles corresponding to a particle volume fractionΦ≈0.001.

It is known that the transition threshold in Poiseuille flow depends on the initial disturbance；one strategy to obtain the threshold for sustained turbulence is to decrease the Reynolds number ofthe turbulent flow until the flow re-laminarizes（see among others［11，12］）.For the single phase flow，we use as initial disturbance high amplitude localized stream-wise vortices，see Ref.［13］for the analyticalexpression ofthe disturbance velocity field.The time histories of the streamwise rms perturbation velocity of the unladen flow are depicted in Fig.1（a）.Note that the rms velocities are normalized by Uband time in units of h/Ub.The criticalReynolds number is found to be 1750＜ Rec＜ 2000 for this particular flow domain and a maximum wall normal velocity of the initial disturbance equal to 10 times of the bulk velocity；fluctuations are sustained at Re=2000 but they decay and eventually vanish at Re=1750.In the next step，we initiate the simulations with a turbulent velocity field at Reb=2000，decrease the Reynolds number to 1800 and run the simulation for a long time:the fluctuations remain and therefore the threshold value ofthe sustained turbulence of the unladen flow is identified approximately，Rec≈1775.

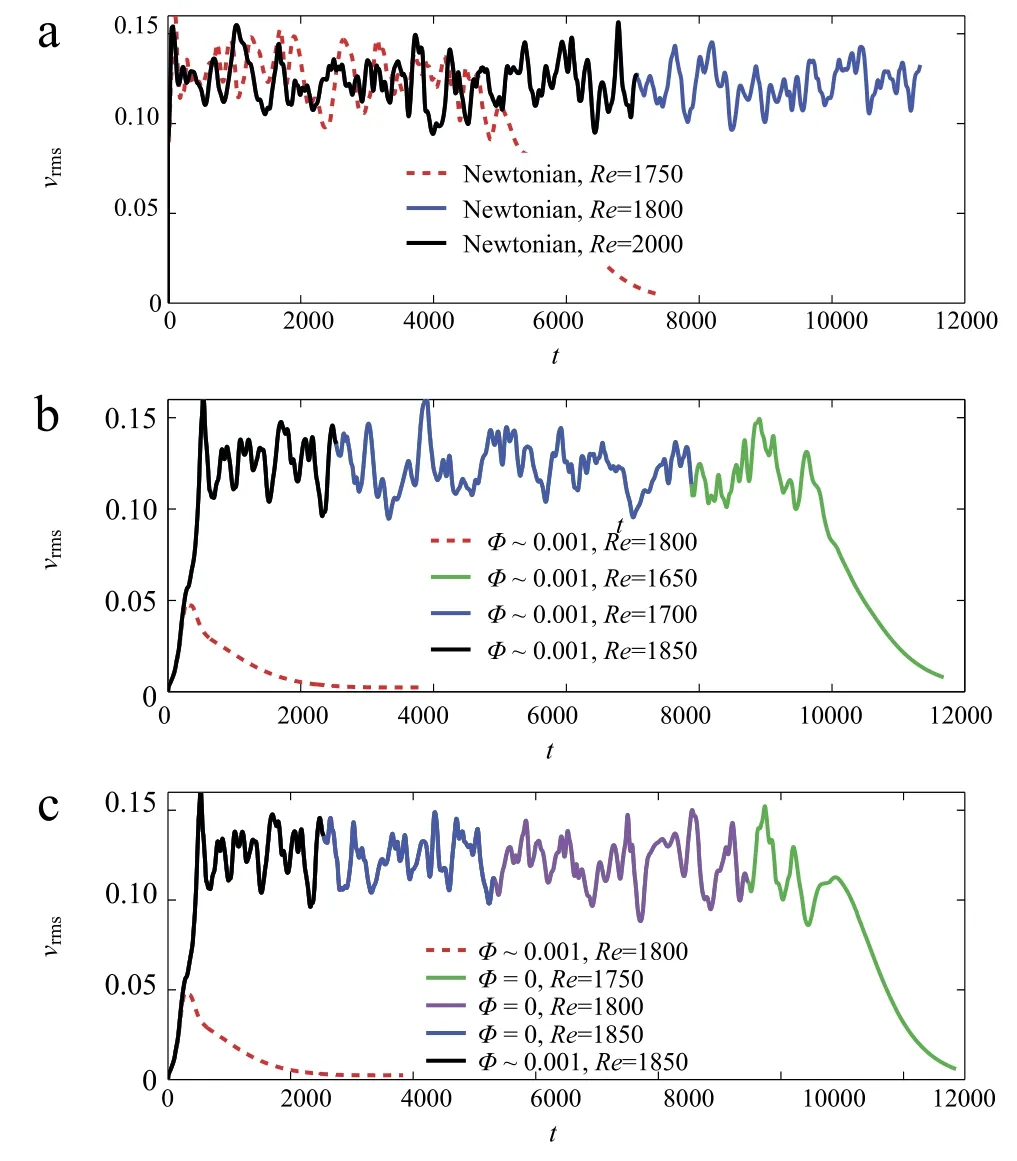
Fig.1.（Color online）Time history of the streamwise velocity fluctuations for（a）Newtonian flow and（b，c）two different paths in particle laden flow（See text）.

The initial condition for the particle-laden flow is given by a random arrangement of the particles，all moving with the local fluid velocity and initial angular velocity equal to half the value of the local vorticity.The initial disturbance source is due to the flow adjustments to the particle presence and therefore depends on the particle position.We initially keep the same initial condition and run simulations at different Reynolds numbers.We observe that the fluctuations，induced by the particles，eventually decay at Re＜1800 while they grow to the turbulent regime at Re＞ 1850（see the fluid streamwise rms velocity in Fig.1（b））.Note that the initial particle arrangement strongly affects the disturbance growth and transition.Therefore，the threshold value of 1800＜ Rec＜ 1850 is only valid for this particular initial configuration；a different behavior is most likely to be observed with another random initial distribution.We will come back to this point when we analyze the trajectory of the particles.As for the unladen flow，we therefore reduce the Reynolds number of the particulate turbulent flow and monitor the Reynolds number at which flow re-laminarizes. The results in the figure reveal that turbulence is sustained at Re=1700 while it decays at Re=1650.Based on these set of simulations，the critical value for sustained turbulence in theparticle laden flow is Re≈ 1675，a value lower than that of the unladen flow in agreement with the experimental data by Matas et al.［2］.The finite-size particles do not only trigger the transition to turbulence but also keep the turbulence at Reynolds number lower than that of the unladen flow.Note that the simulations at which turbulence is sustained are integrated for a time longer than that shown in Fig.1.

To further highlight the difference between laden and unladen flow，we perform a third set of simulations，see Fig.1（c）.In this case starting with a turbulent flow at Re=1850，we first remove the particles and then reduce the Reynolds number until the flow re-laminarizes.The flow sustains turbulence at Re=1800 and it re-laminarizes at Re=1750 providing additional evidence that the threshold for unladen flow is about Re≈ 1775 and that the presence of particles is important to sustain turbulence.For all the cases studied，the fluctuations decay at similar rate once the flow re-laminarizes.We have compared the statistics of the turbulent laden and unladen flows atthe same Reynolds number and observe small differences（not shown here）.

The initial particle configuration plays a vital role to determine the final state of the flow.The flow can become either laminar or turbulent at fixed Reynolds number and number of particles for different initial arrangement of the particles.

To gain physical understanding on the particle influence，we compare the flows at Re=1850 andΦ≈0.001，Re=1800 and Φ≈0.001 and the same initial random arrangement of the particles（denoted as case-Iand case-II），with a simulation at Re=1850 andΦ≈0.001 and a different initial random arrangement（case-III）.Out of these three flows，only case-I is turbulent whereas the other two are laminar.Although the threshold for sustained turbulence for the particle-laden flow is Re≈1675，the disturbances produced by the particles may not be strong enough to bring the system to turbulence.

The time histories of the wall-normal particle position are reported in Fig.2（a）for the three cases introduced above.The particles of case-I（green symbols）and case-II（red symbols），with same initial distribution，initially follow the same path.At t≈300，the trajectories start to deviate and exhibit a completely different behavior at t＞500.Case-I is characterized by a chaotic particle motion，whereas particles migrate towards the center of the channel in case-II；they are eventually found at about 10% of the channel height，from either side of the channel centerline，z≈ 0.45-0.55.This migration is explained by the action of the Saffman lift force（see Refs.［14，15］）.A similar behavior is observed for case-III（blue symbols）when the flow returns to the laminar state although Re=1850.A detailed analysis of the particle final equilibrium position in the presence of inertia and as a function of particle size can be found in the work by Matas et al.［16］for laminar flows.

We display the particle trajectories in the spanwise directions in Fig.2（b）.Forthe laminarcases（case-IIand case-III），the trajectories are almost spanwise independent:particle are transported by the laminar fluid and do not experience strong lateral motions. Significant lateral motions occur，on the contrary，in a turbulent flow.The streamwise particle velocity is shown in Fig.2（c）.Here we observe a final streamwise velocities of about 1.44 at the equilibrium position in the laminar cases，a value larger than the mean velocity（about 1.12）of the turbulent case.

We also examine the particle trajectories in suspensions of higher volume fractions and observe a similar final arrangement of the particles when the flow remains laminar.In other words，particles perturb the flow while migrating towards their equilibrium position.If the flow becomes turbulent during this transient phase，particles will be subject to strong hydrodynamics forces and start to move chaotically；thus，in turn，they contribute to maintain the turbulence.

Fig.2.（Color online）Particle trajectories in:（a）wall normal and（b）spanwise directions，and（c）particle streamwise velocity for case-I（green symbols），case-II（red symbols），and case-III（blue symbols）.See text for the definition.

In order to better understand the mechanism behind the transition in the presence of few particles，we examine the twodimensional spectra of the perturbation kinetic energy，integrated in the wall-normal direction.We shall denote by（α，β）the streamwise and spanwise wavenumbers.The number of Fourier modes employed for each case is enough to reproduce the original field with less than 1%error.

We report the energy spectra pertaining case-I，case-II，and case-III in Fig.3 at three different times in the interval when the behavior of the flow changes considerably，t∈ [300，500]（see Fig.2）.The contours on the top/middle/low panel correspond to case-I/case-II/case-III.The energy spectra at early times clearly reveal that particles contribute to introduce energy to small scales（not shown here）；the modes with high streamwise and spanwise wavenumbers contain non-negligible energy when particles are introduced in the flow.By the time t=300，the energy is transferred back to the larger scales for all cases（see Fig.3（a，d，g））.The peak of the spectra are located atα=0，corresponding to the formation of elongated streaks by the lift-up effect.As discussed in Ref.［17］，the linear lift-up effect，responsible for the streak formation，is hardly affected by the particle presence.Once the streaks have formed，the difference between the three cases is in the energy content of modes withα ≥ 1（this is found to be larger for case-I，the only turbulent flow）.It is likely due to the particular initial condition（case-I vs.case-III）and to the slightly larger Reynolds numbers（case-I vs.case-II）.This is more evident at t= 400，Fig.3（b），where oblique modes are strong enough to destroy the streaks and promote transition.The flow becomes streamwise dependent and the disturbance energy cascades to modes of higher and higher wavenumbers，see Fig.3（c）.The opposite is true for case-II and case-III，Fig.3（e，f，h，i）.Here a single streak resists against the perturbations induced by the particles until it eventually decays.Examining the evolution ofthe perturbation kinetic energy，we thus infer thatthe particles induce streamwise dependentmodes（oblique waves）.If these oblique modes have high enough energy，they promote the streak breakdown and the flow undergoes the transition to turbulence.Conversely，the streaks decay and particles migrate towards their equilibrium position，close to the channel centerline.The initial arrangement of the particles is thus directly connected to the streak breakdown and transition.In the future，it would be interesting to investigate the relative position between vortices/streaks and the particles to access a mechanistic model of their interactions.

Fig.3.Energy spectra for the flow case-I（a-c），case-II（d-f），and case-III（g-i）.（a，d，g）:t=25，（b，e，h）:t=300，（c，f，i）:t=500.

We study the transition to turbulence in channel flow of dilute suspensions of finite-size neutrally buoyant particles and compare the results with those ofthe single-phase flow.The particle volume fraction studied isΦ ≈ 0.001.An immersed boundary solver is used to simulate the particulate flow where lubrication forces and soft sphere collision models are implemented for the near field interactions.

The critical Reynolds number above which turbulence is sustained is Re≈ 1775 for the single-phase flow.It decreases to Rec≈ 1675 for the particulate flow withΦ ≈ 0.001.The disturbances induced by the particles are therefore enough to sustain turbulence at lower Reynolds numbers.The same threshold for the single-phase flow is also obtained，Re≈ 1775，by removing the particles from a turbulent particle-laden flow and decreasing the Reynolds number.

We show that the initial random arrangement of the particles is important to determine whether the flow becomes turbulent. If the flow undergoes transition to turbulence，the particles move chaotically whereas they migrate towards their equilibrium position，close to the centerline，in a laminar flow.This is also observed for flows with a higher number of particles（e.g.50 particles，Φ≈0.005）.

We further examine the two-dimensional energy spectra for three cases:turbulent case-I（Re= 1850）and laminar case-II（Re=1800）with the same initial random arrangement of particles and laminar case-III（Re=1850）but with a different initial arrangement.The results indicate that the transition in case-I is due to higher energy content in oblique disturbance modes.The particles can trigger strong enough oblique modes that promote the streak breakdown.The streaks undergo secondary instabilities and breakdown to turbulence，before being regenerated by non-linear interactions in a self-sustaining cycle［9］.In the other two cases，the streaks induced initially by the lift-up effect decay slowly in time and the particles migrate towards the centerline.

Acknowledgments

This work was supported by the European Research Council Grant No.ERC-2013-CoG-616186，TRITOS and by the Swedish Research Council（VR）.The authors acknowledge computer time provided by SNIC（Swedish NationalInfrastructure for Computing）.

［1］J.Klinkenberg，G.Sardina，H.C.De Lange，L.Brandt，Numericalstudy oflaminarturbulent transition in particle-laden channel flow，Phys.Rev.E 86（2013）043011.http://dx.doi.org/10.1103/PhysRevE.87.043011.

［2］J.P.Matas，J.F.Morris，É Guazzelli，Transition to turbulence in particulate pipe flow，Phys.Rev.Lett.90（2003）1. http://dx.doi.org/10.1103/PhysRevLett.90.014501.

［3］Z.Yu，T.Wu，X.Shao，J.Lin，Numerical studies of the effects of large neutrally buoyant particles on the flow instability and transition to turbulence in pipe flow，Phys.Fluids 25（2013）043305.http://dx.doi.org/10.1063/1.4802040.

［4］V.Loisel，M.Abbas，O.Masbernat，E.Climent，The effect of neutrally buoyant finite-size particles on channel flows in the laminar-turbulent transition regime，Phys.Fluids 25（2013）123304.http://dx.doi.org/10.1063/1.4848856.

［5］I.Lashgari，F.Picano，W.-P.Breugem，L.Brandt，Laminar，turbulent and inertialshear-thickening regimes in channelflow ofneutrally buoyantparticle suspensions，Phys.Rev.Lett.113（2014）254502. http://dx.doi.org/10.1103/PhysRevLett.113.254502.

［6］Q.Zhang，A.Prosperetti，Physics-based analysis of the hydrodynamic stress in a fluid-particle system，Phys.Fluids 22（2010）03330. http://dx.doi.org/10.1063/1.3365950.

［7］M.Uhlmann，An immersed boundary method with direct forcing for the simulation of particulate flows，J.Comput.Phys.209（2005）448-476. http://dx.doi.org/10.1016/j.jcp.2005.03.017.

［8］W.-P.Breugem，A second-order accurate immersed boundary method for fully resolved simulations of particle-laden flows，J.Comput.Phys.231（2012）4469-4498.http://dx.doi.org/10.1016/j.jcp.2012.02.026.

［9］J.M.Hamilton，J.Kim，F.Waleffet，Regeneration mechanisms of near-wall turbulence structures，J.Fluid Mech.287（1995）317-348. http://dx.doi.org/10.1017/S0022112095000978.

［10］L.Xi，M.D.Graham，Active and hibernating turbulence in minimal channel flow of Newtonian and polymeric fluids，Phys.Rev.Lett.104（2010）218301. http://dx.doi.org/10.1103/PhysRevLett.104.218301.

［11］A.Schmiegel，B.Eckhardt，Persistent turbulence in annealed plane Couette flow，Europhys.Lett.51（2000）395-400.http://dx.doi.org/10.1209/epl/i2000-00507-2.

［12］J.Philip，P.Manneville，From temporal to spatiotemporal dynamics in transitional plane Couette flow，Phys.Rev.E 83（2011）036308. http://dx.doi.org/10.1103/PhysRevE.83.036308.

［13］D.S.Henningson，J.Kim，On turbulent spots in plane Poiseuille flow，J.Fluid Mech.228（1991）183-205.http://dx.doi.org/10.1017/S0022112091002677.

［14］P.G.Saffman，The lift on a small sphere in a slow shear flow，J.Fluid Mech.22（1965）385-400.http://dx.doi.org/10.1017/S0022112065000824.

［15］G.Segre，A.Sliberberg，Radial particle displacements in Poiseuille flow of suspensions，Nature 189（1961）209-210.http://dx.doi.org/10.1038/189209a0.

［16］J.P.Matas，J.F.Morris，É Guazzelli，Inertial migration of rigid spherical particles in Poiseuille flow，J.Fluid Mech.515（2004）171-195. http://dx.doi.org/10.1017/S0022112004000254.

［17］L.Brandt，The lift-up effect:The linear mechanism behind transition and turbulence in shear flows，Eur.J.Mech.B Fluids 47（2014）80-96. http://dx.doi.org/10.1016/j.euromechflu.2014.03.005.

∗Corresponding author.

E-mail address：imanl@mech.kth.se（I.Lashgari）.

http://dx.doi.org/10.1016/j.taml.2015.04.004

2095-0349/©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

*This article belongs to the Fluid Mechanics