On two distinct Reynolds number regimes of a turbulent square jet

Minyi Xu∗，Jianpeng Zhang，Pengfei Li，Jianchun Mi

aMarine Engineering College，Dalian Maritime University，Dalian 116026，China

bState Key Laboratory of Turbulence&Complex Systems，College of Engineering，Peking University，Beijing 100871，China

On two distinct Reynolds number regimes of a turbulent square jet

Minyi Xua，∗，Jianpeng Zhangb，Pengfei Lib，Jianchun Mib

aMarine Engineering College，Dalian Maritime University，Dalian 116026，China

bState Key Laboratory of Turbulence&Complex Systems，College of Engineering，Peking University，Beijing 100871，China

a r t i c l e i n f o

Article history：

Received 9 August 2014

Received in revised form

25 December 2014

Accepted 22 January 2015

Available online 17 April 2015

Square jet

Hot-wire

Reynolds number

Small-scale turbulence

Mean energy dissipation rate

The effects ofReynolds number on both large-scale and small-scale turbulence properties are investigated in a square jet issuing from a square pipe.The detailed velocity fields were measured at five different exit Reynolds numbers of 8×103≤ Re≤ 5×104.It is found that both large-scale properties（e.g.，rates of mean velocity decay and spread）and small-scale properties（e.g.，the dimensionless dissipation rate constant A= εL/〈u2〉3/2）are dependent on Re for Re≤ 3×104or Reλ≤ 190，but virtually bec/ome Re-independent with increasing Re or Reλ.In addition，for Reλ＞ 190，the value of A= εL/〈u2〉32in the present square jet converges to 0.5，which is consistent with the observation in direct numerical simulations of box turbulence，but lower than that in circular jet，plate wake flows，and grid turbulence. The discrepancies in critical Reynolds number and A=εL/〈u2〉3/2among different turbulent flows most likely result from the flow type and initial conditions.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）. Introduction Turbulent jets are applied in various industrial mixing processes，e.g.，dispersal and combustion.In these flows，large-scale motions whose scale is close to global flow scale contain most of the kinetic energy and dominate the transfer of momentum，heat and mass，while the small-scale turbulence spanning the dissipative and inertial ranges brings different species together at the molecular level［1，2］.

Previous investigations by Dimotakis［3，4］indicated that a mixing transition，beyond which the amount of mixed fluid become Re-independent for Re＞ Recrand the flow becomes fully developed turbulence，occurs in jets and other shear flows.This can be observed widely in turbulence.Here Recris a critical Reynolds number.Dimotakis claimed that，the fully-developed turbulence，the existence of a range of scales（uncoupled from the large scales and free from the viscosity effect）is a necessary condition.A outer-scale Reynolds number Re=Uδ/ν＞ 10000-20000 or a Taylor Reynolds number Reλ= 〈u2〉1/2λ/ν≥ 100-140 is required by the resulting fully-developed turbulent.Here u represents the longitudinal component of the fluctuating velocity，λ ≡ 〈u2〉1/2〈（∂u/∂x）2〉−1/2andνthe kinematic viscosity.This observation is supported by Fellouah and Pollard［5］and Mi et al.［6］in their investigations of circular jets.In addition，Mi etal.［6］suggested thatεmay be wellestimated byε=A1〈u2〉3/2/L for Re≥10000 or Reλ≥110 andε=A2ν〈u2〉/L2for Re＜10000 or Reλ＜110；here L is the integral length-scale of turbulence while A1and A2are experimental constants.

Compared to circular jets，noncircular jets have been found more effective in mixing with ambient fluid［7，8］.In the case of square jets，Xu et al.［9］measured square jet flows emanating from a long square tube using hot wire measurements in the range of 8000≤ Re≤ 50000.They found that all the far-field rates of the mean velocity decay and spread，and the asymptotic value of the streamwise turbulent intensity，decrease as Re increases for Re≤ 3×104，while they become almost Re-independent for Re＞ 3×104.However，Xu et al.［9］did not provide information on the influence of Reynolds number on small-scale turbulent properties of square jets.In this sense，is there any difference between the critical transition Reynolds numbers for large-scale and small-scale turbulences in the square jet？In addition，the critical Reynolds number in the square jet seems higher than that of circular jets.What is（are）the reason（s）for the critical Reynolds number varying from flow to flow？To address these important questions，we conduct the present study to investigate the effects of Reynolds numberon both large-scale and small-scale turbulentproperties of a square jet at five different Reynolds numbers between 8000 and 50000.

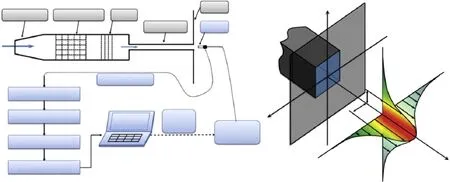
Fig.1.（a）Experimental setup and（b）3D square jet nozzle exit，notations，and coordinate system.Uc/2is the axial mean velocity at either Y1/2or Z1/2.

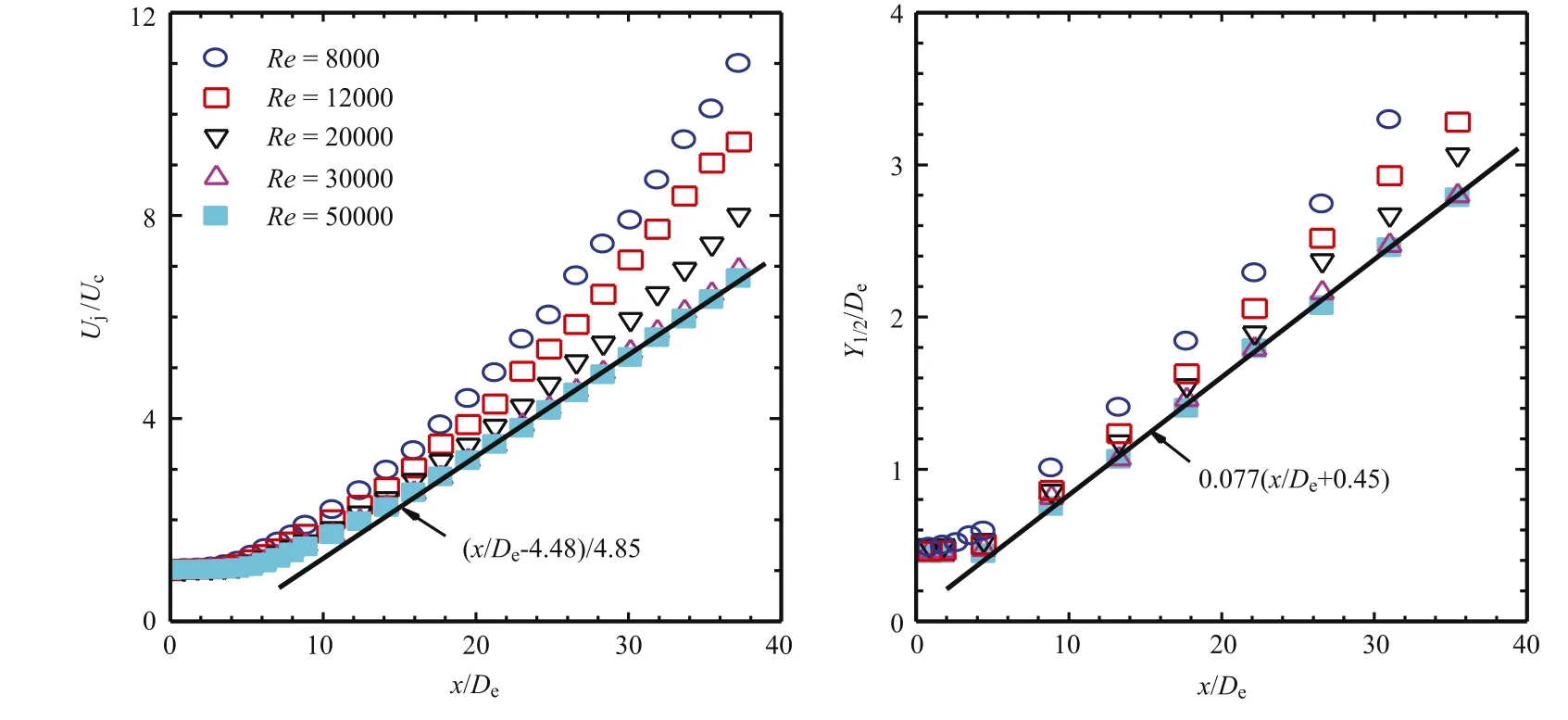
Fig.2.Streamwise variations of（a）inverse centerline mean velocity Uj/Ucand（b）normalized half-width in the x-y plane Y1/2/Defor Re=8000-50000.

Content Detailed description of the present measurement is referred to Xu et al.［9］，only a brief version is provided here and the data processing methods for small-scale turbulent statistics are carefully introduced in Mi et al.［10］.The present square jets were generated from a nozzle system whose schematic diagram is shown in Fig.1（a）.The present facility consisted of a square duct with the width of the square duct H=2.5 cm，and the length of approximately 2 m.The nominal opening area A=6.25 cm2and the equivalent diameter De≡ 2（A/π）1/2was approximately 2.82 cm.The mean streamwise velocity Ujat the center of the square exit plane was varied over the range 4.2≤Uj≤26.4 m/s，corresponding to a Reynolds number range 8× 103＜ Re＜5× 104，with Re≡ UjDe/ν.With fc= 20 kHz（an identical cut-off frequency），velocity signals were low-pass filtered for all measurements to eliminate excessively high-frequency noise and to avoid aliasing.The voltage signals were then digitized on a personal computer at fs= 40 kHz via a 12 bit A/D converter and each record had a duration of about 80 s.The present study corrected the spatial attenuation of the single wire due to the wire lengthλw≈1 mm using the procedure of Wyngaard［11］，which was developed in spectral space to account for the integration effect on Fourier components of the velocity.To remove the effect of high frequency noise，the present data were filtered using the digital scheme of filtering high-frequency noise proposed by Mi et al.［10，12］.In this context，the present study estimatesε from hot-wire measurements of u（t），using the isotropic relation ε=15ν〈（∂u/∂x）2〉together with modified Taylor’s hypothesis∂u/∂x=（Uc+u）−1∂u/∂t，rather than U−1c∂u/∂t［13］.

Figure 2 presents the streamwise variation of the inverse centerline mean velocity Ucnormalized by the exit centerline mean velocity Uj，i.e.，Uj/Ucand the normalized half width Y1/2/Dein the range of 8000≤Re≤50000.To quantitatively study the dependence of Uj/Ucand Y1/2/Deon Re，the well-known self-preserving relations are applied，i.e.

where KUand KYare the jet velocity decay rate and spread rate，x is axial downstream distance measured from the nozzle exit，and xUand xYare the x-locations of the virtual origin of Eqs.（1）and（2）. Figure 3 shows the variations of the jet velocity decay rate KUand spread rate KYwith the Reynolds number.KUand KYsignificantly depend on Re for Re≤3×104，as demonstrated clearly in Fig.3，but appear to independent with further increasing Re.Thus，there seems to be a critical Reynolds number of Recr=30000 for the large-scale turbulence in the present square jet flow.

To investigate the influence of Re on small-scale turbulence of the present square jet，Fig.4 presents the streamwise evolution of the normalized dissipation ratein the range ofRe=8000-50000.Clearly，as the jet flow develops downstream，ε∗decreases rapidly with downstream distance x and follows the self-preserving relation of the mean energy dissipation rate in the self-preserving circular jet［6］，i.e.

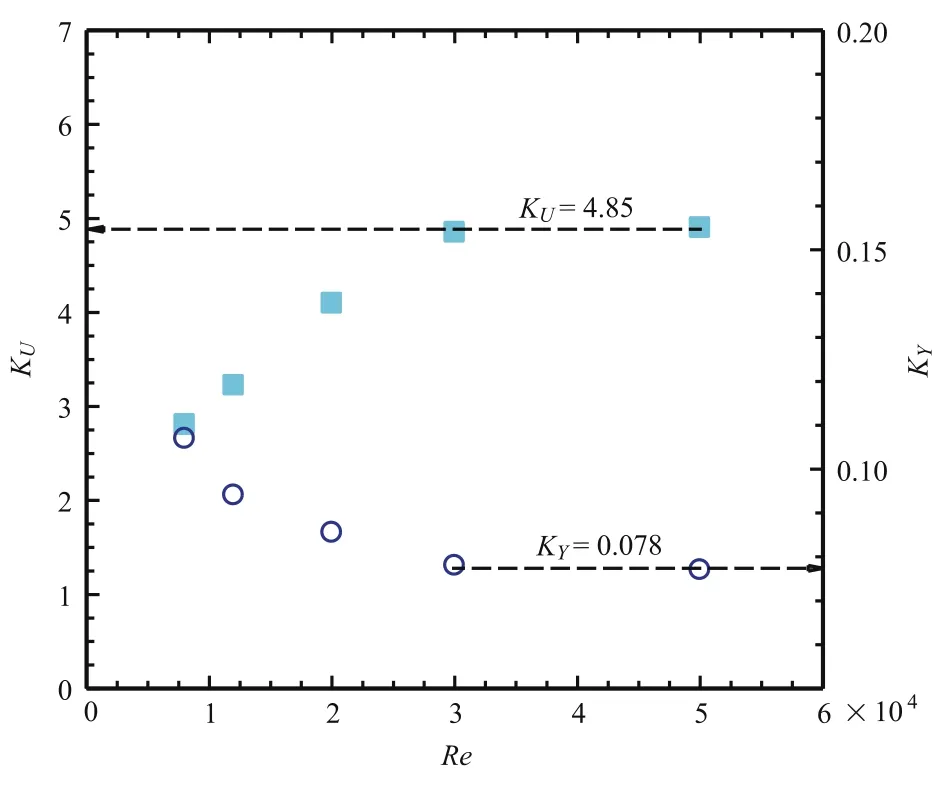
Fig.3.Re-dependence of the mean velocity decay KUand spread rates KY.

Fig.4.Streamwise evolution of the normalized energy dissipation rateε∗=The data from Mi et al.［6］is also added for comparison.

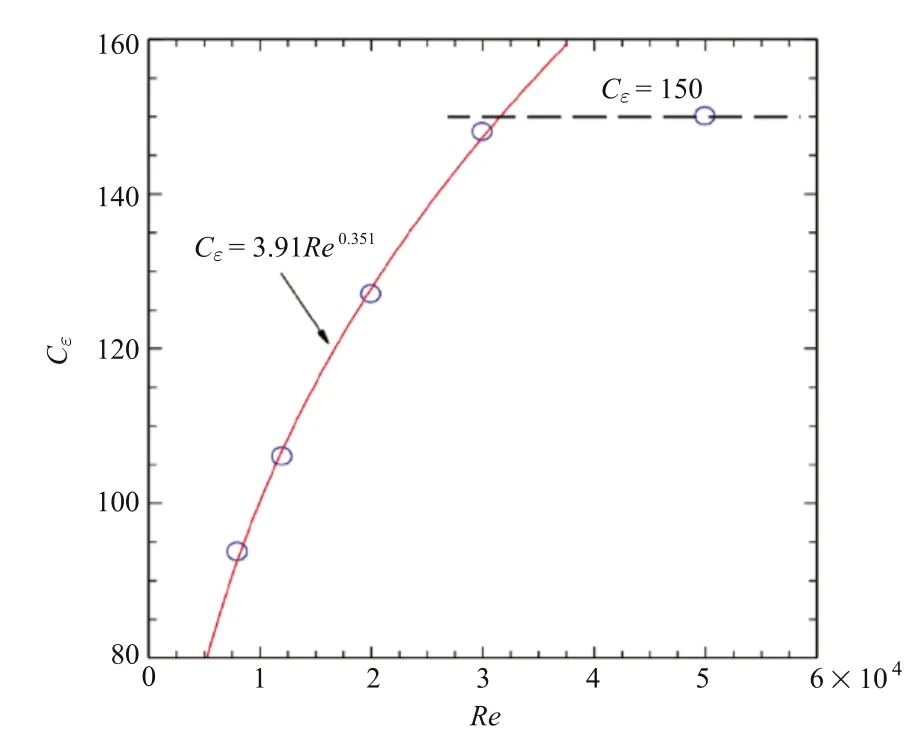
Fig.5.Dependence on Re of the prefactor Cε.

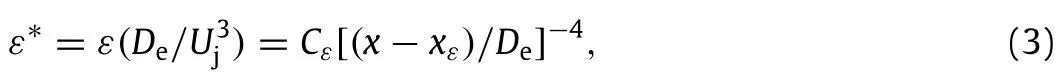
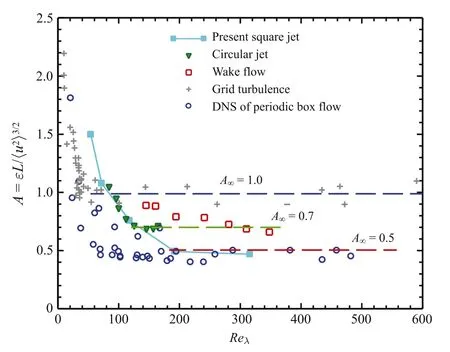
Fig.6.Dependence of A= εL/〈u2〉3/2on Reλ.Symbols:■-■，present square jet；▼，circular jet turbulence［6］；+，grid turbulence，compiled by Sreenivasan［14］；⃝，directnumericalsimulation（DNS）ofperiodic box turbulence，compiled by Burattini et al.［15］；□，wake flow［15］.

where Cεis the prefactor，and xεis the virtual origin location.The value of Cεcan be determined by fitting measured data with Eq.（3），which is shown in Fig.5.For Re≤3×104，as observed from Fig.6，the prefactor（Cε）of Eq.（3）increases with Re.By fitting the value of Cεfor Re≤3×104，the relationship between Cεand Re is Cε≈3.91Re0.351.For Re＞3×104，all the measured data ofε∗becomes constant and collapses virtually onto a single horizontal line with Cε≈ 150，suggesting thatε∗becomes nearly independent of the Reynolds number.Thus，the critical transition Reynolds numbers for both large-scale and small-scale turbulence of the square jet is the same，i.e.，Recr≈ 30000.However，this value is higher than that in a circular jet，whose critical Reynolds number Recris about 10000，across which the jet turbulence behaves distinctly，see Ref.［6］.In addition，it is worth noting that the normalized energy dissipation rateε∗and the prefactor Cεare higher for the present square jet than the circular jet measured in Mi et al.［6］. It indicates that the mean turbulent energy is dissipated at higher rate and mixing is enhanced for the square jet，compared to the circular jet.

Further，the results A=εL/〈u2〉3/2estimated from the present square jet flow for Re=8000-50000 or Reλ=54-316 are shown in Fig.6.A number of previous datasets for circular jet，grid turbulence，wake flows，DNS of box turbulence are also added for comparison.It is interesting to note that the value of A deceases from 1.5 to 0.5，as Reλincreases from 54 to 190.For Reλ≥190，the value of A seems to asymptote to a constant value of 0.5，denoted by A∞. In a circular jet，Mi et al.［6］found that，for Reλ＜130，A obviously decreases notably with increasing Reλ，while A becomes nearly independent of Reλat Reλ≥130.Sreenivasan［14］checked the dependence of A on Reλover a greater range of Reλthrough collecting a number of previous datasets for grid turbulence produced by biplane square meshes，and found that the critical Reynolds number Reλ，cr≈ 50 for grid turbulence.For DNS of period box flow，Reλ，crseems to be about 200，see Fig.6.The present results show that the critical Reynolds number is unlikely to lie in just a narrow range ofReynolds numbers as suggested by Dimotakis［3］generally for any turbulent flows.Figure 6 also demonstrates that A∞differs appreciably for various flows.Explicitly indicated on the plot are A∞≈0.5 for the present square jet and DNS of periodic box turbulence［15］；A∞≈ 0.7 for a circular jet［6］and plate wake［15］；A∞≈1.0 for the grid turbulence［14，16］.

The above discrepancies in A∞and criticalReynolds numberare most likely to result from the flow type and initial conditions［6］. This indicates that〈u2〉3/2/L is notproportionalto the rate atwhichenergy transferred from the large-scale eddies［17］.Mazellier and Vassilicos［18］indicated that the nonuniversal asymptotic of the dimensionless dissipation rate constant A stems from its universal dependence on the number of large-scale eddies，which strongly varies from flow to flow.Compared to the smooth contraction circular jet studied by Mi et al.［6］and wake flow in Ref.［15］，the long pipe square jet produces a power-law profile of the mean velocity and a very thick fully-turbulent boundary-layer at exit，thus resulting in the less large-scale eddies in the near field and smaller A∞.Despite A∞and Reλ，crvarying for different flows，according to Fig.6，A = εL/〈u2〉3/2in general decreases with increasing Reλuntil Reλ=Reλ，cr.For Reλ＞ Reλ，cr，there is a good constancy ofεL/〈u2〉3/2，i.e.，A=A∞with almost constant oforder unity.

This study has successfully clarified by experiments the effects of Reynolds number on both the large-scale and small-scale turbulence properties from the transition region to the selfpreserving far field of a square jet.Consistent with the largescale properties（e.g.，the centerline mean velocity and half-width），the small-scale properties（e.g.，the normalized mean dissipation rate）of the square jet have been found to significantly depend on Reynolds number for Re≤30000 or Reλ＜190，but weaken with further increasing Re or Reλ.For Reλ＞ 190，the value of A= εL/〈u2〉3/2in the present square jet converges to 0.5，consistent with the observation in DNS of box turbulence，but lower than that in circular jet，grid turbulence and wake flows.The discrepancies in A= εL/〈u2〉3/2and critical Reynolds number among different turbulent flows are most likely to result from the flow type and initial conditions.Compared to the smooth contraction circular jet and wake flow，the long pipe square jet produces less large-scale eddies，thus resulting in smaller value of the asymptotic of the dimensionless dissipation rate constant.

Acknowledgments

This work was supported by the Fundamental Research Funds for the Central Universities，China（3132015027），the general science research project of the education department of Liaoning Province，China（L2013198），and the Natural Science Foundation of Liaoning Province，China（2014025012）.The present experiment was conducted in Prof.Andrew Pollard’s Lab in Queen’s University.

［1］K.R.Sreenivasan，R.A.Antonia，The phenomenology of small-scale turbulence，Annu.Rev.Fluid Mech.29（1997）435-472. http://dx.doi.org/10.1146/annurev.fluid.29.1.435.

［2］G.J.Nathan，J.Mi，Z.T.Alwahabi，G.J.R.Newbold，D.S.Nobes，Impacts of a jet’s exit flow pattern on mixing and combustion performance，Prog.Energy Combust.Sci.32（2006）496-538.http://dx.doi.org/10.1016/j.pecs.2006.07.002.

［3］P.E.Dimotakis，The mixing transition in turbulent flows，J.Fluid Mech.409（2000）69-98.http://dx.doi.org/10.1017/S0022112099007946.

［4］P.E.Dimotakis，Turbulent mixing，Annu.Rev.Fluid Mech.37（2005）329-356. http://dx.doi.org/10.1146/annurev.fluid.36.050802.122015.

［5］H.Fellouah，A.Pollard，The velocity spectra and turbulence length scale distributions in the near to intermediate regions of a round free turbulent jet，Phys.Fluids 21（2009）115101.http://dx.doi.org/10.1063/1.3258837.

［6］J.Mi，M.Xu，T.Zhou，Reynolds number influence on statistical behaviors of turbulence in a circular free jet，Phys.Fluids 25（2013）075101. http://dx.doi.org/10.1063/1.4811403.

［7］E.Gutmark，F.Grinstein，Flow control with noncircular jets，Annu.Rev.Fluid Mech.31（1999）239-272.

［8］M.Xu，J.Zhang，J.Mi，G.J.Nathan，P.A.M.Kalt，Mean and fluctuating velocity fields of a diamond turbulent jet，Chin.Phys.B 22（2013）034701. http://dx.doi.org/10.1088/1674-1056/22/3/034701.

［9］M.Xu，A.Pollard，J.Mi，F.Secretain，H.Sadeghi，Effects of Reynolds number on some properties of a turbulent jet from a long square pipe，Phys.Fluids 25（2013）035102.http://dx.doi.org/10.1063/1.4797456.

［10］J.Mi，M.Xu，C.Du，Digital filter for hot-wire measurements of small-scale turbulence properties，Meas.Sci.Technol.22（2011）125401. http://dx.doi.org/10.1088/0957-0233/22/12/125401.

［11］J.Wyngaard，Measurementofsmall-scale turbulence structure with hotwires，J.Phys.E:Sci.Instrum.1（1968）1105-1108.http://dx.doi.org/10.1088/0022-3735/1/11/310.

［12］J.Mi，R.C.Deo，G.J.Nathan，Fast-convergent iterative scheme for filtering velocity signals and finding Kolmogorov scales，Phys.Rev.E 71（2005）066304. http://dx.doi.org/10.1103/Physreve.71.066304.

［13］P.Burattini，R.A.Antonia，L.Danaila，Similarity in the far field of a turbulent round jet，Phys.Fluids 17（2005）025101. http://dx.doi.org/10.1063/1.1833414.

［14］K.Sreenivasan，On the scaling of the turbulence energy dissipation rate，Phys. Fluids 27（1984）1048.http://dx.doi.org/10.1063/1.864731.

［15］P.Burattini，P.Lavoie，R.A.Antonia，On the normalized turbulent energy dissipation rate，Phys.Fluids 17（2005）http://dx.doi.org/10.1063/1.2055529.

［16］L.Mydlarski，Z.Warhaft，On the onset of high-Reynolds-number gridgenerated wind tunnel turbulence，J.Fluid Mech.320（1996）331-368. http://dx.doi.org/10.1017/S0022112096007562.

［17］H.Mouri，A.Hori，Y.Kawashima，K.Hashimoto，Large-scale length that determines the mean rate of energy dissipation in turbulence，Phys.Rev.E 86（2012）026309.http://dx.doi.org/10.1103/PhysRevE.86.026309.

［18］N.Mazellier，J.C.Vassilicos，The turbulence dissipation constant is not universal because of its universal dependence on large-scale flow topology，Phys.Fluids 20（2008）http://dx.doi.org/10.1063/1.2832778.

∗Corresponding author.

E-mail address：xuminyi@dlmu.edu.cn（M.Xu）.

http://dx.doi.org/10.1016/j.taml.2015.04.001

2095-0349/©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

*This article belongs to the Fluid Mechanics