Enhancing heat transfer at the micro-scale using elastic turbulence

R.D.Whlley，W.M.Abed，D.J.C.Dennis，R.J.Poole，b，∗

aSchool of Engineering，University of Liverpool，Liverpool L69 3GH，UK

bLMFA，Université de Lyon，Ecole Centrale de Lyon，69134 Ecully，France

Letter

Enhancing heat transfer at the micro-scale using elastic turbulence

R.D.Whalleya，W.M.Abeda，D.J.C.Dennisa，R.J.Poolea，b，∗

aSchool of Engineering，University of Liverpool，Liverpool L69 3GH，UK

bLMFA，Université de Lyon，Ecole Centrale de Lyon，69134 Ecully，France

a r t i c l e i n f o

Article history：

Received 23 June 2014

Received in revised form

8 August 2014

Accepted 27 October 2014

Available online 14 March 2015

Elastic turbulence

Viscoelasticity

Serpentine channel

Micro-mixing

Heat transfer

Small concentrations of a high-molecular-weight polymer have been used to create so-called‘‘elastic turbulence’’in a micro-scale serpentine channel geometry.It is known that the interaction of large elastic stresses created by the shearing motion within the fluid flow with streamline curvature of the serpentine geometry leads initially to a purely-elastic instability and then the generation of elastic turbulence.We show that this elastic turbulence enhances the heat transfer at the micro-scale in this geometry by up to 300%under creeping flow conditions in comparison to that achieved by the equivalent Newtonian fluid flow.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

In so-called‘‘creeping flow’’，i.e.，flows for which the Reynolds number（Re）remains small（Re＜ 1），Newtonian fluids remain laminar and steady.Consequently efficient mixing and heat transfer to the fluid are problematic for very viscous systems or liquid flows at small scales（e.g.，microfluidics）as they are essentially diffusion/conduction dominated.One method to circumnavigate these problems is to make the fluid non-linear by the addition of small amounts of high molecular-weight polymer.The resulting viscoelastic solution enables fluid flows at arbitrarily small values of Re to exhibit‘‘turbulent-like’’characteristics such as randomly fluctuating fluid motion excited across a broad range of temporal and spatial scales［1-6］.Steinberg and co-workers［1-4］showed that highly-elastic viscoelastic fluids can undergo a series of flow transitions from viscometric laminar flow，to periodic flow，to apparently chaotic flow，and then to fully developed elastic turbulence（ET）in conditions of negligible inertia（Re＜1）and this has been shown in a range of flows:swirling flow between parallel disks［1，4，5］，in serpentine or wavy channels［2-4，6］and in concentric cylinder devices［4，7］.The instabilities and resulting nonlinear interactions are‘‘purely-elastic’’in nature—driven by the elastic（normal）stresses developed in flow—and occurat Reynolds numbers farremoved fromthe usualturbulence observed for Newtonian fluids which is inertial in nature（critical Re on the order of 1000 for internal flows）.Although the original work of Groisman and Steinberg［1］has elicited a significant degree of interest（and the passive-scalar mixing effectiveness ofthe regime has been mentioned repeatedly［1，3-7］）outside of the quantitative studies on passive scalar mixing［8，9］，little work has yet been carried out to assess this effectiveness in other typical‘‘mixing’’scenarios.An exception to this is the study of Poole et al.［10］where ET was used to create oil in polymer solution emulsions in a swirling flow between parallel disks arrangement（similar to that used in Ref.［1］）where for a Newtonian oil and continuous phase，at identical conditions，no emulsification occurred at all.Flows containing streamline curvature are ideal for encouraging elastic instabilities and elastic turbulence as itis generally accepted thatpurely-elastic instabilities arise as a consequence of both elastic normal stresses and streamline curvature［11］—although some analyticalwork［12］and experimental evidence［13］are beginning to show that even parallel shear flows may exhibit ET providing the initial perturbation is sufficiently strong.

The growth of‘‘microfluidic’’research，and the major fundamental interest and applications of such flows［14］，has revealed previously unobserved instabilities and flow phenomena that occur solely due to viscoelasticity.In fact some of the key publications on ET［4，6，13］have used such micro-geometries to access the required parameter space（low inertia，high elastic stresses）. The small scale nature of such flows leads directly to the viscoelastic behavior observed:the small length scale simultaneously makes the Reynolds number（Re≡ρUD/µ）small and the Deborah（De≡λU/D）or Weissenberg（Wi≡λU/D）numbers，which characterize the degree of elasticity in the flow，large（whereρis density，U a velocity scale，D a length scale，µa viscosity，and λa characteristic or relaxation time for the fluid）.The De number is a ratio of characteristic timescales（fluid to flow）and the Wi number is the ratio of elastic to viscous forces.Thus at the microscale，due to the small flow time scales and the high strain rates attainable，viscoelastic effects will become important even for dilute solutions which appear Newtonian in macro-scale flows.In the current letter we utilize this effect in a microfluidic serpentine channel［3，15-17］.Typical Wi numbers required to observe elastic turbulence have been reported as:swirling flow between parallel disks Wi∼3.5［1］，Taylor-Couette flow Wi∼ 4［4］，serpentine channel flow Wi∼ 3.2（onset），＞ 6.7（developed）［4］，1.4-3.5（onset），10（developed）［3］，7.5-15（developed）［6］.By the use of high shear rates，viscous solvents，and an extremely highmolecular-weight polymer，we reach Wi∼100.

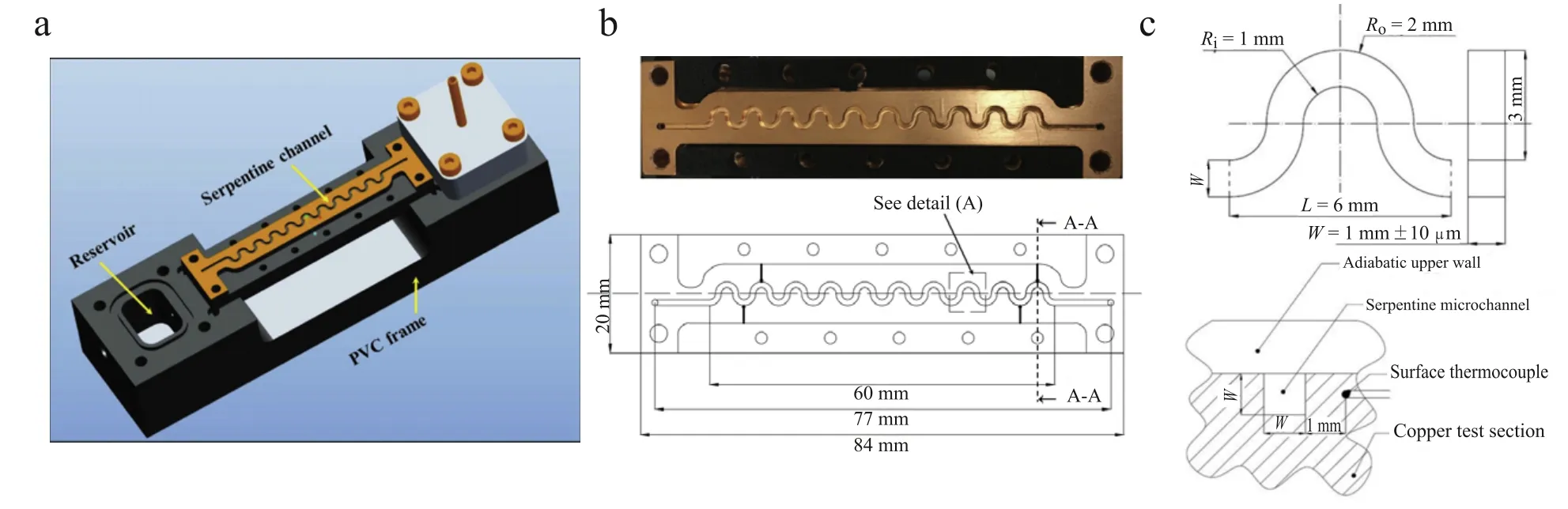
Fig.1.（a）Isometric view of the experimental facility，（b）plan views of the serpentine channel，and（c）detailed view and cross section of the serpentine channel.

As far as the effect of ET on heat transfer is concerned，no work has been reported hitherto.For Newtonian fluids at low Reynolds numbers，e.g.，in microfluidics applications，both thermal and viscous development are short（∼pipe diameter）and the Nusselt number（Nu）is an order one constant which is independent of the Reynolds number.The heat transfer is conduction-dominated and long fluid residence times are required to achieve significant temperature increases.In contrast，if（inertial）turbulentconditions can be reached then heat can be transferred much more efficiently.For example in a straight pipe at a Reynolds number of 3000 the Nusselt number is increased by a factor of 10 above the laminar value（for identical Prandtl numbers）.It might be anticipated that such large increases in heat transfer coefficients may also occur with ET provided the base flow is free from convection（and therefore heatis treated as a passive scalar）.The currentpaper addresses this question and demonstrates the potential of using ET to enhance heat transfer in microfluidics applications.

The heat transfer measurements were conducted in a serpentine channel as shown in Fig.1（a）.The serpentine channel was micro machined into a piece of copper and consisted of 20 halfloops with inner and outer radii of 1 mm and 2 mm，respectively. The serpentine channel was flanked on either side by straight inlet and outlet channel sections and had a total length of 77 mm（see Fig.1（b））.The channel had a square cross section with a depth and width of 1.075±0.01 mm（see Fig.1（c））.The entire channel was mounted on a PVC substrate，which encompassed two separate reservoirs（one at either end of the channel），and the channel was enclosed by an upper wall fabricated from PVC.

The entire facility was housed in a Techne TE-10A water bath continuously-stirred and maintained at a temperature of 30°C（leading to typical fluid temperature increases of 4°C-8°C）. The copper bottom and copper side walls guaranteed isothermal boundary conditions and the insulating properties of the PVC ensured an adiabatic boundary condition on the upper wall.The surface temperature of the serpentine channel was monitored by four K-type thermocouples each embedded 1 mm from the channel side walls.The enhancement of heat transfer generated by the complex fluid flowing through the serpentine channel was quantified by measuring the temperature difference between the two reservoirs（before and after the serpentine channel）with K-type thermocouples.The K-type thermocouples had a quoted uncertainty of±1°Cand were calibrated againsta mercury thermometer of certified accuracy（±0.1°C）.

The pressure drop along the channel was measured by a Validyne DP15-26 differential pressure transducer.The pressure transducer estimated the streamwise pressure gradient（ΔP），from which the friction factor（f=[ΔP/（0.5ρU2）]（Dh/L），where U is the average velocity，Dhis the hydraulic diameter，and L is the pathlength equal to 111.25 mm in our set-up）could be determined，by measuring the difference in pressure across two pressure taps installed on the upperwallofeach reservoir.The pressure transducer used two different diaphragms to capture the full working range: one had a working range of 0.2 bar whilst the other had a range of 2 bar，both are said to be accurate to±0.25%full scale，and both diaphragms were periodically calibrated against an MKS Baratron differential pressure transducer（1000 torr fsd）.

Fluid was pumped through the serpentine channel by a regulated pressure vessel.The fluid was discharged into a beaker and weighed by a Denver TP-1502 precision balance allowing a measurement of the mass flow rate（uncertainty±0.03 mg）. The working fluids were solutions of a high-molecular-weight（∼18×106g/mol）polyacrylamide supplied by polysciences，with mass concentrations of 80 ppm and 120 ppm in a Newtonian solvent comprised of 65%sucrose，1%NaCl，and 34%water（all by mass）.At these concentrations the solutions are either dilute or semi-dilute as c/c∗∼1，where c is the concentration of polymer and c∗is the critical overlap concentration which is approximately 100 ppm（0.01%）when determined from intrinsic viscosity measurements（assuming c∗is roughly the inverse of the intrinsic viscosity）.Allrheologicalmeasurements ofthe fluids were performed with a TA Instruments AR1000N controlled-stress rheometer with a cone-and-plate geometry（60 mm diameter，2°cone angle）.

Those shown in Fig.2（a）are shear viscosity（η）measurements versus shear rate（˙γ）for the Newtonian and complex fluids used in the present study.The Newtonian fluid has a constant shear viscosity of 0.164 Pa·s at 20°C，and the polymer solutions both exhibit slight shear-thinning behavior.The shear viscosity data of the complex fluids have been fitto the Carreau-Yasuda model［18］，which allows an estimate of the shear viscosity（ηCY）values at any shear rate:

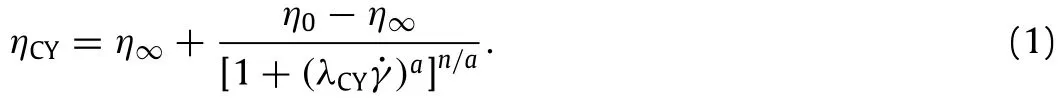
In Eq.（1），η0is the zero-shear-rate viscosity，η∞is the infiniteshear-rate viscosity，λCYis a constant which characterizes theonset of shear-thinning，n is a power-law index，and a is a fitting parameter.We use this shear-rate dependent viscosity to define our Reynolds number Re = ρUDh/ηCHand Prandtl number（Pr=cηCH/kf，where c is the heat capacity and kfis the thermal conductivity of the fluid）where the viscosityηCHis determined at a characteristic shear rate corresponding to˙γ =U/Dhand at a mean film temperature（（¯To+¯Ti）/2）where¯Toand¯Tiare the mean fluid temperature at the outlet and inlet reservoirs，respectively. The specific heatand thermalconductivity were assumed to be that of the solvent following several other studies［19，20］.

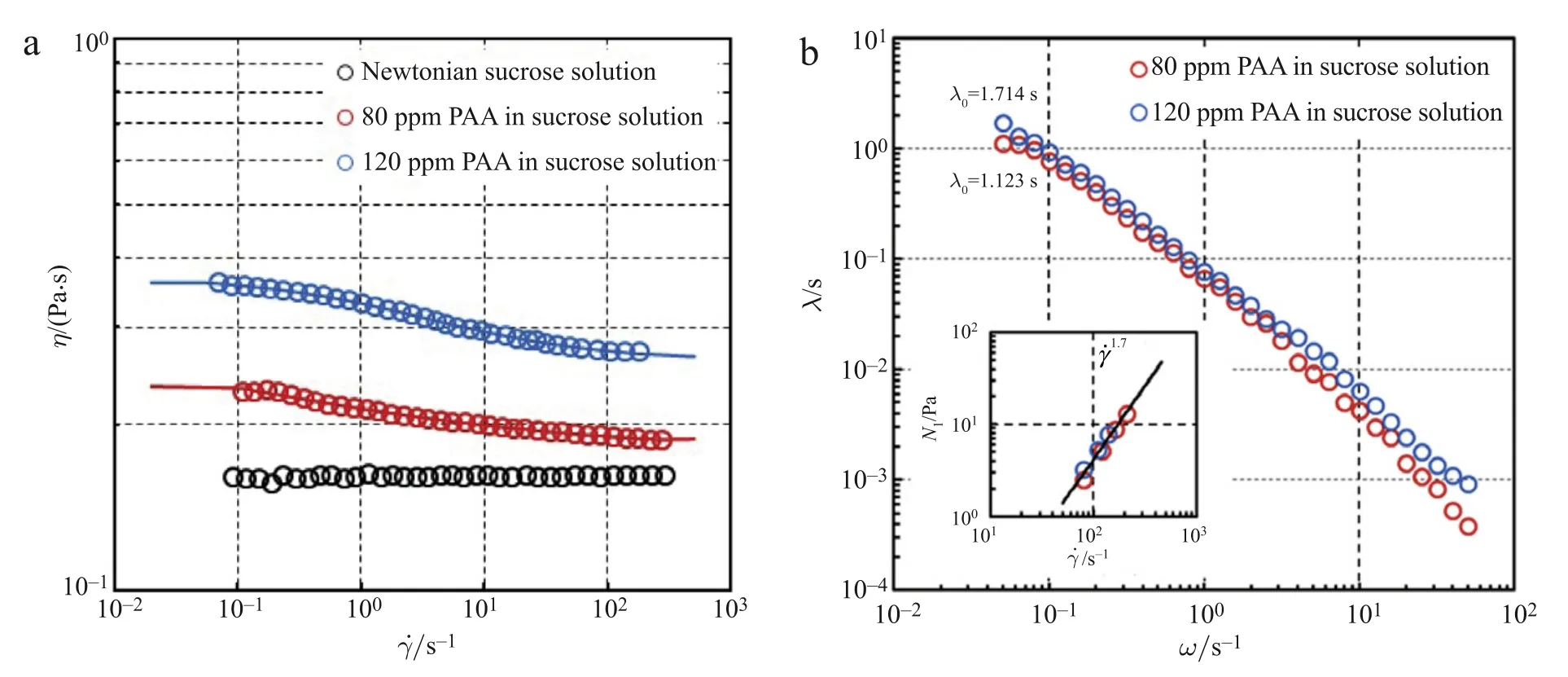
Fig.2.（a）Shear viscosity and（b）relaxation time determined from small amplitude oscillatory shear measurements versus shear rate/frequency:Newtonian fluid（⃝），80 ppm PAA（），120 ppm PAA（），and the solid continuous lines in plot（a）are Carreau-Yasuda fits.Inset in plot（b）shows first normal-stress difference versus shear rate. All data measured at 20°C.

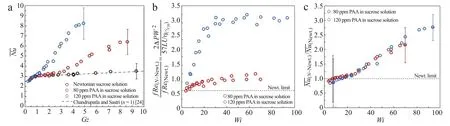
Fig.3.（a）Nusselt number versus Graetz number，（b）pressure-drop，and（c）normalized Nusselt number versus Weissenberg number.Newtonian fluid（⃝），80 ppm PAA（），120 ppm PAA（）.Numerical solutions for a developing laminar flow［24］（---）.Data shown in plot（c）is same as data shown in plot（a）and so Graetz number is also varying slightly for the two polymer solutions.

The shear-rate dependent polymer relaxation time（λ）has been estimated by small-amplitude-oscillatory-shear（SAOS）measurements（λ=G′/（G′′ω）），where G′is the storage modulus，G′′is the loss modulus，andωis the applied angular velocity（see Fig.2（b））. The longest relaxation times（λ0）have been obtained from the SAOS measurements，by estimating the relaxation times in the limitofthe angular velocity tending to zero（see Table 1）.The slight concentration dependence of the relaxation time suggests that the highest concentration solution may just be semi-dilute in agreement with the critical overlap concentration estimate from the intrinsic viscosity.It was also possible to measure the first normalstress difference for both solutions，although the values are very close to the resolution of the instrument:estimating a relaxation time from this data over the limited shear rate range available produces data broadly in agreement with the values estimated over the same frequency range in SAOS（on the order of 10−3-10−2s）. Estimates of the relaxation time from stress relaxation measurements，e.g.，following Ref.［21］，were not attempted.The important fluid properties for the fluids used in this study are listed in Table 1 at both 20°C and 26°C（the latter being a typical mean film temperature）.

To quantify the enhancement of heat transfer by elastic turbulence we calculate the Nusselt number（Nu）defined as

where˙m is the mass flow rate，Asis the surface area of the channel， andis the log-mean temperature difference with¯Twbeing the mean wall temperature.

Figure 3（a）shows the changes in the Nusselt number with increasing Graetz number（Gz=（Dh/L）·Re·Pr）.The Newtonian fluid flow collapses to the numerical predictions for a thermally developing laminar flow through a straight square duct［24］suggesting the curvature of the serpentine channel has little influence for Newtonian fluids at such low Graetz numbers.Beyond a certain flowrate，the addition of viscoelasticity enhances the heat transfer causing an increase in the Nusselt number.From previous experimental and numerical work for isothermal flows in our group［15-17］and elsewhere［2-4，6］，we know that creeping（Re→ 0）viscoelastic fluid flows through such serpentine channels firstly at low Wi number develop a steady secondary flow［15］before the onset of a purely-elastic instability leads to oscillatory timedependent flow at Weissenberg numbers of order one（∼0.6［16］，1.4-3.5［3］，3.2［2，4］）.Beyond this first linear instability the flowbecomes increasingly complex and，as previously discussed，developed elastic turbulence is observed beyond Wi＞ 7-15［2-4，6］. Hence for the parameter space of our investigation we are at a sufficiently high Wi number to be in a fully elastic turbulence regime and therefore we believe the increase in heat transfer we observe here is due to elastic turbulence，which has been created by the non-linear interaction between elastic stresses generated within the polymer solutions and the streamline curvature of the serpentine geometry［2-4］.This scenario is illustrated in the pressure-drop data shown in Fig.3（b）where we can see thatatvery low flow-rates（Wi＜ 5）the pressure-drop and Nusselt number（Fig.3（c））are，to within the experimental uncertainties，essentially the same as the Newtonian values.Thus，perhaps surprisingly，the stationary secondary-flow driven by the interaction of the first normal-stress difference and channel curvature shown numerically in isothermalflow by Poole etal.［15］does notappear to modify the heattransfersignificantly in contrastto the secondary-flows driven by the second normal-stress difference for much more concentrated polymer solutions observed in straight ducts［20］.Beyond this Weissenberg number the purely-elastic instability leads to an increase in the pressure-drop but the Nusselt number is only marginally affected（5＜ Wi＜ 25）.Beyond Wi=25，where the pressure drop data plateaus，significant increases in normalized Nusselt number are observed（Fig.3（c））.At the highest flowrates achievable this leads to a maximum 300%increase compared to the equivalent Newtonian value（e.g.，identical Graetz number）.

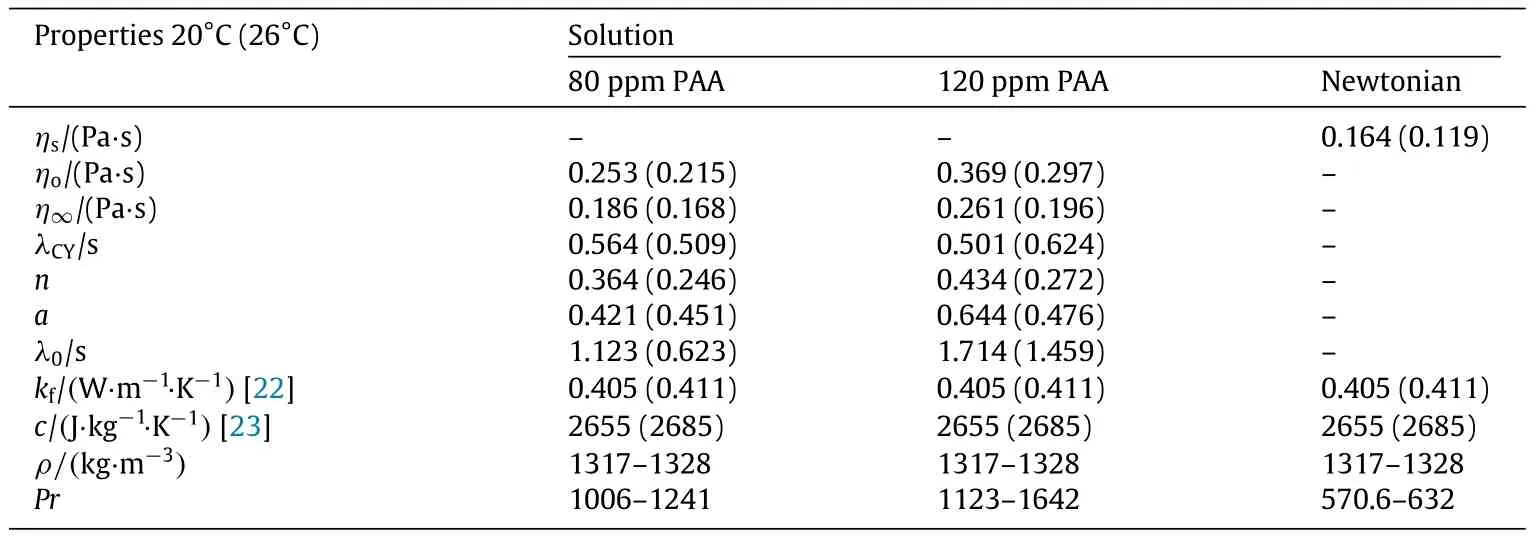
Table 1 Fluid properties at 20°C and 26°C（in parenthesis）.

In this experimental investigation we have shown that it is possible to enhance the heat transfer by up to 300%in micro-scale geometry at low Graetz number using elastic turbulence.At the same flow-rates for equivalent Newtonian fluids，e.g.，either the solvent or identical Graetz number，the Nusselt number remains within 10%of the conduction limit.The elastic turbulence has been created by the non-linear interaction between elastic stresses generated within the flowing high-molecular-weight polymer solutions and the streamline curvature of the serpentine geometry.Outside of its fundamental scientific interest，the use of elastic turbulence to enhance the heat transfer could have impacts for micro-mixing technologies and in the design of lab-on-a-chip devices.

Acknowledgments

Waleed M.Abed gratefully acknowledges the financial support from The Higher Committee for Education Development in Iraq and The Iraqi Ministry of Higher Education and Scientific Research. Some of this paper was written whilst the corresponding author was a visiting professor at LMFA Université de Lyon Ecole Centrale de Lyon and this support is gratefully acknowledged.

［1］A.Groisman，V.Steinberg，Elastic turbulence in a polymer solution flow，Nature 405（2000）53-55，http://dx.doi.org/10.1038/35011019.

［2］A.Groisman，V.Steinberg，Efficient mixing at low Reynolds number using polymer additives，Nature 410（2001）905-908，http://dx.doi.org/10.1038/ 35073524.

［3］T.Burghelea，E.Segre，I.Bar-Yosef，A.Groisman，V.Steinberg，Chaotic flow and efficient mixing in microchannel with a polymer solution，Phys.Rev.E 69（2004）066305，http://dx.doi.org/10.1103/PhysRevE.69.066305.

［4］A.Groisman，V.Steinberg，Elastic turbulence in curvilinear flows of polymer solutions，New J.Phys.6（2004）1-48，http://dx.doi.org/10.1088/1367-2630/6/1/029.

［5］B.A.Schiamberg，L.T.Shereda，H.Hu，R.G.Larson，Transitional pathway to elastic turbulence in torsional，parallel-plate flow ofa polymer solution，J.Fluid Mech.2006（2006）191-216，http://dx.doi.org/10.1017/S0022112006009426.

［6］F.C.Li，H.Kinoshita，X.B.Li，M.Oishi，T.Fujii，M.Oshima，Creation of very-low-Reynolds-number chaotic fluid motions in microchannels using viscoelastic surfactant solution，Exp.Thermodyn.Fluid Sci.34（2010）20-27，http://dx.doi.org/10.1016/j.expthermflusci.2009.08.007.

［7］J.Beaumont，N.Louvet，T.Divoux，M.A.Fardin，H.Bodiguel，S.Lerouge，S. Manneville，A.Colin，Turbulent flows in highly elastic wormlike micelles，Soft Matter 3（2013）735-749，http://dx.doi.org/10.1039/c2sm26760h.

［8］T.Burghelea，E.Segre，V.Steinberg，Mixing by polymers:Experimental test of decay regime of mixing，Phys.Rev.Lett.92 （2004）164501，http://dx.doi.org/10.1103/PhysRevLett.92.164501.

［9］Y.Jun，V.Steinberg，Mixing of passive tracers in the decay Batchelor regime of a channel flow，Phys.Fluids 22（2010）123101，http://dx.doi.org/10.1063/1. 3522400.

［10］R.J.Poole，B.Budhiraja，A.R.Cain，P.A.Scott，Emulsification using elastic turbulence，J.Non-Newton.Fluid Mech.177-178（2012）15-18，http://dx.doi. org/10.1016/j.jnnfm.2012.03.012.

［11］E.S.G.Shaqfeh，Purely elastic instabilities in viscometric flows，Ann.Rev.Fluid Mech.28（1996）129-185，http://dx.doi.org/10.1146/annurev.fl.28.010196. 001021.

［12］A.N.Morozov，W.V.Saarloos，An introductory essay on subcritical instabilities and the transtion to turbulence in visco-elastic parallel shear flows，Phys.Rep. 447（2007）112-143，http://dx.doi.org/10.1016/j.physrep.2007.03.004.

［13］L.Pan，A.N.Morozov，C.Wagner，P.E.Arratia，Purely nonlinear elastic instability in parallel shear flows，Phys.Rev.Lett.110（2013）174502，http://dx.doi.org/10.1103/PhysRevLett.110.174502.

［14］T.M.Squires，S.R.Quake，Microfluidics:Fluid physics atthe nanoliter scale，Rev. Modern Phys.77（2005）977-1026，http://dx.doi.org/10.1103/RevModPhys. 77.977.

［15］R.J.Poole，M.A.Alves，A.Lindner，Viscoelastic secondary flows in serpentine channels，J.Non-Newton.Fluid Mech.201 （2013）10-16，http://dx.doi.org/10.1016/j.jnnfm.2013.07.001.

［16］J.Zilz，R.J.Poole，M.A.Alves，D.Bartolo，B.Levache，A.Lindner，Geometric scaling of a purely elastic flow instability in serpentine channels，J.Fluid Mech. 712（2012）203-218，http://dx.doi.org/10.1017/jfm.2012.411.

［17］J.Zilz，C.Schäfer，C.Wagner，R.J.Poole，M.A.Alves，A.Lindner，Serpentine channels:quantitative micro-rheometers for fluid relaxation times，Lab Chip 14（2014）351-358，http://dx.doi.org/10.1039/c3lc50809a.

［18］K.Yasuda，R.C.Armstrong，R.E.Cohen，Shear flow properties of concentrated solutions of linear and star branched polystyrenes，Rheol.Acta 20（1981）163-178，http://dx.doi.org/10.1007/BF01513059.

［19］R.P.Chhabra，J.F.Richardson，Non-Newtonian Flow and Applied Rheology: Engineering Applications，Butterworth-Heinemann，ISBN:978-0-7506-8532-0，2008.

［20］J.P.Hartnett，M.Kostic，Heat transfer to a viscoelastic fluid in laminar flow through a rectangularchannel，Int.J.Heat Mass Transfer 28（1985）1147-1155，http://dx.doi.org/10.1016/0017-9310（85）90122-X.

［21］Y.Liu，Y.Jun，V.Steinberg，Concentration dependence of the longest relaxation times of dilute and semi-diulte polymer solutions，J.Rheol.53（2009）1069-1085，http://dx.doi.org/10.1122/1.3160734.

［22］M.Werner，A.Baars，F.Werner，C.Eder，A.Delgado，Thermal conductivity of aqueous sugar solutions under high pressure，Int.J.Thermophys.28（2007）1161-1180，http://dx.doi.org/10.1007/s10765-007-0221-z.

［23］F.A.Mohos，Confectionery and Chocolate Engineering Principles and Applications，John Wiley&Sons，Ltd.，ISBN:978-1-4051-9470-9，2010.

［24］A.R.Chandrupatla，V.M.Sastri，Laminar forced convection heat transfer of a non-Newtonian fluid in a square duct，J.Heat Mass Transfer 20（1977）1315-1324，http://dx.doi.org/10.1016/0017-9310（77）90027-8.

∗Corresponding author.

E-mail address：robpoole@liv.ac.uk（R.J.Poole）.

http://dx.doi.org/10.1016/j.taml.2015.03.006

2095-0349/©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

*This article belongs to the Fluid Mechanics