New applications of a generalized Hooke’s law for second gradient materials

K.Enakoutsa

Center for Advanced Vehicular Systems，Mississippi State University，Mississippi State，MS 39762，USA

New applications of a generalized Hooke’s law for second gradient materials

K.Enakoutsa

Center for Advanced Vehicular Systems，Mississippi State University，Mississippi State，MS 39762，USA

a r t i c l e i n f o

Article history：

Received 5 February 2014

Received in revised form

19 April 2014

Accepted 23 June 2014

Available online 17 April 2015

Second gradient theory

We provide analytical solutions to the problems of a circular bending of a beam in plane strain and the torsion of a non-circular cross-section beam，the beams obeying a second-gradient elasticity law proposed by the author，following a previous suggestion of Dell’Isola et al.（2009）.The motivation was to find benchmark analytical solutions that can serve to grasp the physical foundations of second gradient elasticity laws for heterogeneous materials.The analytical solution of the circular beam problem presents the additionaladvantage to establish some nice properties on the unknown second gradientelastic moduli introduced by Enakoutsa（2014）model and the classical elasticity constants for both incompressible and compressible heterogeneous elastic materials.A framework to find the elastic moduli of the new model is also proposed.

©2015 Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics. This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/ by-nc-nd/4.0/）.

There has been a recent increase of interest in non-local constitutive models for elastic materials with microstructure including elastomers，steel cables，rubber bands，springs and lycra clothes，etc.The motivation is that the nonlocal framework involves some characteristic length scale related to microstructure effects that emerge during the deformation of the material.Some years ago，the works of Mindlin［1，2］have proposed a generalized elastic framework to describe the linear behavior of isotropic materials with microstructure.Their approach was in line with the so-called Cosserat and Cosserat’s［3］elasticity theory with constrained rotations.Mindlin’s［1，2］theory also refers to the couple stresses theory of Mindlin and Tiersten［4］and Koiter［5］，strain gradient theory of Toupin［6］，micropolar elastic theory of Green and Rivlin［7］，microstretch and the micropolar elastic theories of Eringen［8］，or the non-local elastic theory of Eringen［9］.Generalized elasticity theories，involving the second gradient of the strain，were able to predict，in a continuum manner，as such phenomena as capillarity and cohesion in elastic media.Also，a recent finding by Alibert et al.［10］has linked the predominance of higher-grade effects to some specific design of the microstructure in some heterogeneous elastic media；only a generalized constitutive elasticity theory can enable the prediction of this feature.Furthermore，higher-order gradientelastic approaches have permitted to predict（1）meaningful wave dispersion inelastic materials［11］，（2）size-scale effects observed in the bending of marbles or epoxy polymeric beams experiments［12，13］.

A generalized elasticity theory（denoted in this work by GLPD elasticity model）was applied by Gologanu et al.［14］to add an ad hoc hypoelasticity law to a second gradient model for ductile fracture in porous plastic metals.The motivation of these authors for doing so was to obtain，in this way，a framework which can easily lend itself into a finite element subroutine.Their proposal involves the natural Hooke’s law，which relates the ordinary Cauchy stress to the strain rate，and a generalized elasticity law connecting the 3rd-rank tensor the GLPD theory involves and the gradient of the strain rate.Although Enakoutsa［15，16］has demonstrated that numerical predictions based on the GLPD elasticity model are meshindependent，the way the elasticity law was accounted for was not satisfactory from a theoretical point of view.Indeed，it does not rely on any serious physical or mathematical justification.This is a good reason to adopt the proposal by Enakoutsa［17］to replace the original GLPD elasticity model by one that is based on some sound physical justification，following an earlier suggestion of Dell’Isola etal.［18］.Asimple boundary value problem，a sphericalshellmade of the newly proposed model and subjected to axisymmetric loading conditions，was used to assess the validity of Enakoutsa’s［17］proposal.The success ofsuch an assessmentopens the door forfurther studies on the illustrations of the proposal by Enakoutsa［17］. The problems under consideration，this time，are the circular bending of a beam under plane strain conditions and the torsion of a non-circular cross-section beam，the beams modeled by the newly proposed second gradient elasticity.The use of a strain gradienttheory for these problems is totally justified，since the deformation in the beams during the loading history is highly nonhomogeneous（for instance，the fibers located on the inner face of the bending are in compression，while those located on the outer face of the bending are in tension，creating a gradient of the strain in the beam）and cannot be captured by a standard Hooke’s law.The remaining part of this paper is organized as follows.As a first step，we give a brief review of the original and modified version of the GLPD elasticity model.Next，we present the procedure of the analytical solution of the circular bending problem.The analytical expressions of the velocity and strain rate fields，as well as the ordinary and higher-order stress fields are obtained in this section as a function of the position of the fibers in the beam.This section ends with some remarks on the newly obtained analyticalsolution. In the subsequent，we develop the solution of the second problem，the torsion of a non-circular cross-section beam.Here also，the analytical expressions of the displacement，strain rate，stress and the moment fields are provided as a function of the wrapping function the displacementfield involves.The particularcase where the second-gradient effects are negligible is discussed.Finally，we suggest a framework to determine the unknown elastic moduli the new second-gradient elasticity model involves.

We provide a short but complete review of the original GLPD elasticity theory（the details of this theory can be found in Refs.［14，16］）as well as its modified version，recently proposed by Enakoutsa［17］.The original GLPD theory involved a homogenized Cauchy stress and a higher-order stress（of moment type）fields，Σ and M，respectively，that must satisfy the balance equations

obtained from the application of the principle of virtual work（in the absence of body force and moment）to virtual powers of internal and external forces（P（i），P（e））defined as

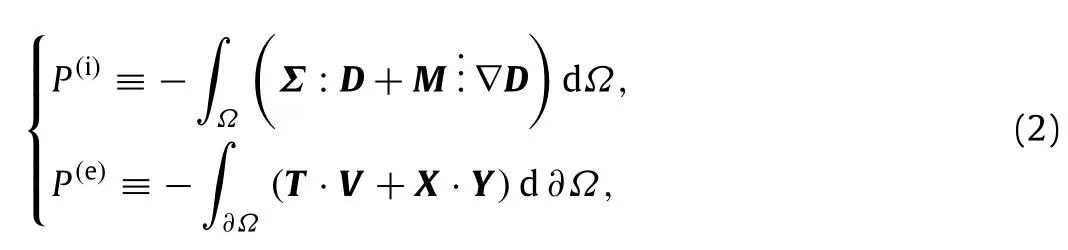
whereΩdenotes the domain considered，∂Ωthe boundary of the domain，D the Eulerian strain rate，∇D the gradient of this strain，T a macroscopic surface traction，and the factor of X a‘‘surface moment’’.The application of the principle of virtual work also yields the following boundary conditions:

assuming that the boundary of the body∂Ωis smooth.The complete form of these conditions can be found in Refs.［19，20，18］.The original GLPD elasticity law consists of two constitutive relations obtained as

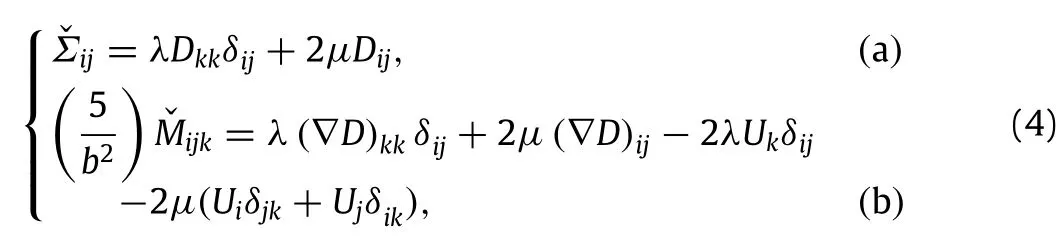
where variablesˇΣijandˇMijkare the（objective）Jaumann derivatives ofΣijand Mijk，the parametersλandµare Lamé’s elastic coefficients，U≡ （Ui）（1≤i≤3）is a vector defined as

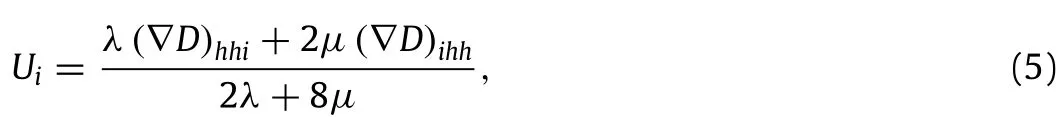
and b is a characteristic length scale the GLPD elastic theory involves.The relation（4）was used to implement Gologanu et al.’s［14］model for plastic porous metals into SYSTUS finite element code developed by Engineering Systems International.The‘‘ad hoc’’nature of this law motivated a recent development of an alternative law by Enakoutsa［17］，which consists of replacing Eq.（4）（b）by the one which is physically sound.A review of this new law is presented in the subsequent.

The new proposal followed a previous work by Dell’Isola et al.［18］and was derived from some thermodynamics and material symmetry characterization arguments.The fundamental idea of this proposal was that the free energy which the ordinary and higher order stresses derived from is a quadratic form of both the Eulerian strain rate and its gradient；this quadratic form involves 4th，5th，and 6th-rank tensors which obey some symmetry properties.In the new proposal，the expressions of the ordinary and higher-order stresses are given by the relations

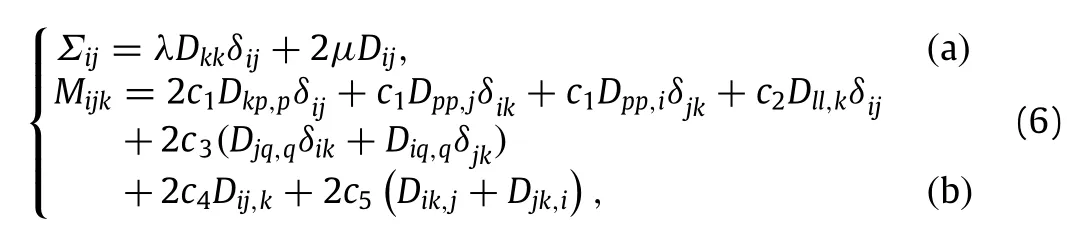
whereλandµare the two standard Lamé’s elastic moduli，δijdenotes the Kronecker delta symbol，and parameter ci（1≤i≤5）represents certain material constants.

Note that the rate form in Eq.（4）was not introduced here，since its usefulness is only applied in the contextofthe numericalimplementation into a finite element code.The 3rd-rank tensor M defined in the model proposed by Enakoutsa［17］is symmetric over its first two indices.This tensor must balance with the ordinary Cauchy stress tensorΣthrough the equilibrium equation（1），as required.The 3rd-rank tensor M is also termed by‘‘hyperstress’’in reference to the contact actions it represents in second gradient theories.In addition，it can represent internal forces having the nature of a 3rd-rank tensor.In some physical theories，it has been used to model micromagnetism effects［21］while in the context of ductile fracture of porous plastic metals［14］it was interpreted as a stress field of moment-type representing the strain-gradient effects.The 3rd-rank tensorcan also representthe microstructure effects in linear elastic materials［1，2］.In this study，we shall assume thatthe 3rd-rank tensor M and the gradientofthe strain∇D are introduced to representthe effects ofheterogeneities（points defects，pores，small cracks，microstructures）in the materials and the gradientofthe deformation these heterogeneities generate during the deformation.There are at least two points of difference between the GLPDelasticity theory and the one proposed by Enakoutsa［17］. The first one is the presence of the vector U in GLPD elasticity law，which represents an additional constraint equation to be solved，especially when dealing with the numerical implementation of constitutive elastoplastic relations involving this elasticity law.Another difference lies in the constitutive constants the two models involve，three constants for the GLPD elasticity law for seven for the new proposal.Of course this number is high，especially from the pointofview ofthe experimentalcharacterization ofthese constants；however，some way or another，it is the price to pay to obtain a physically sound model，which is one of the requirements to obtain reliable physics-based constitutive models.In what follows we apply the new proposal Eq.（6）to derive analytical solutions for two problems:the circular bending of a beam under plane strain conditions and the torsion of a non-circular cross-section beam. The geometry of the first problem is a rectangular cross-section beam of center O and thickness 2h in the direction e2of an orthogonal reference system（e1，e2，e3）.This beam is bent in plane strain in the plane（O，e1，e2）.The lateral boundary condition enforces a linear variation of the horizontal component D11of the strain upon the variable X2；thus this component is defined as D11=BX2.The parameter B is a non-zero constant，independent with respect tothe coordinate X2but not with respect to the time，representing the curvature of the neutral fiber，i.e.，X2=0.Whatever the behavior considered the strain field is defined by

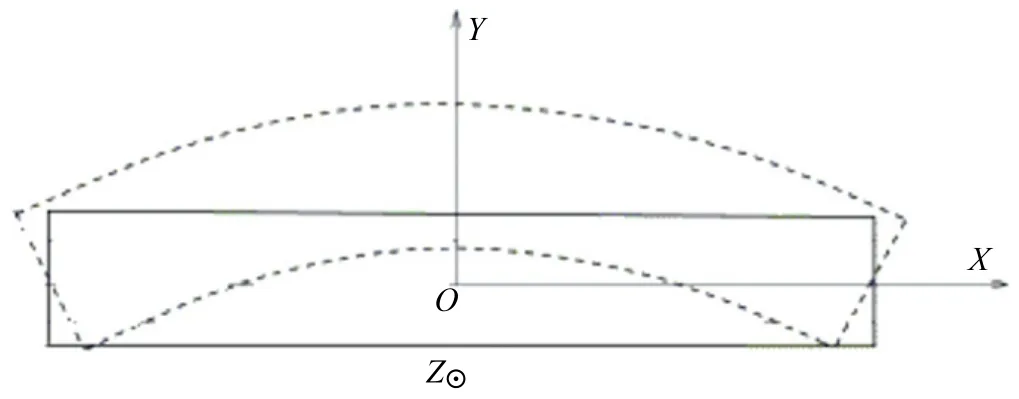
Fig.1.Circular bending of a beam in plane strain.

where g（X2）is some function.Figure 1 is an illustration ofthe problem which is solved within the linearized context（small displacements，small strains）.

The boundary conditions are obtained from the application of the principle of virtual work and the assumption that the mechanical fields in the problem only depend on the variable X2. The determination of the boundary conditions is also based on the symmetry properties of the stressesΣand M which yield the following expression for the virtual power of internal forces P（i）

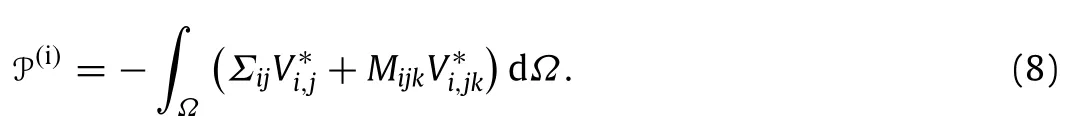
An integration by parts of Eq.（8）conserving only the terms on the surface in the principle of virtual work reads

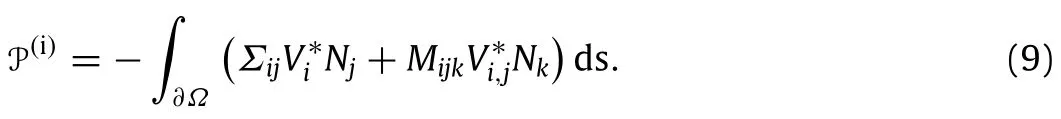
The second term in the right-hand side of Eq.（9）gives

on the upper side of the beam where the variableis independent of；however，the other derivativesandare related to，this requires a second integration by parts. Considering the surface term in the application of the principle of virtual work，we get

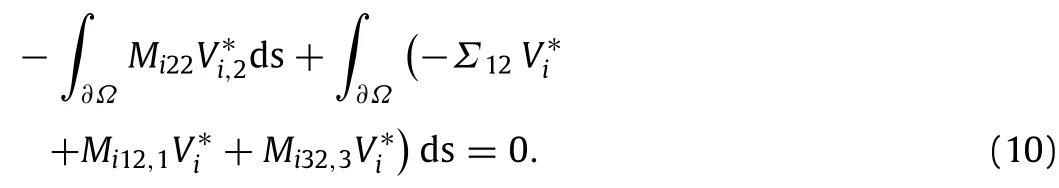
Setting separately the co-factors ofandto zero，the boundary conditions of the circular bending problem reads

Because the moment field in this problem is assumed to be independentofthe coordinates X1and X3，the relations（11）reduce to

In the subsequent，we shall assume that the beam is modeled by the constitutive relations（6）and we solve the problem for the deformation，stress and moment fields.

The componentΣ22of the stress tensorΣis linear with respect with X2and vanish on the face X2= ±h（see the boundary conditions（12）associated to the problem）；thus this component vanishes at every point of the beam.The shearing components of the stress being equal to zero，the only non-zero components of the stress tensorΣareΣ11andΣ33.Combining Eq.（6）（a）and the plane strain assumption in the problem，we obtain

The non-zero components of the strain，D11and D22，are deduced from Eq.（6）（a）as

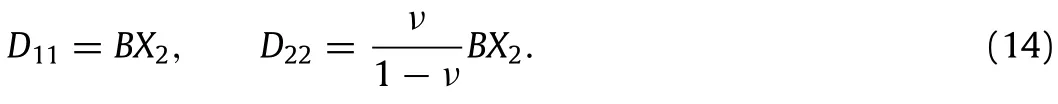
Note that the stress and strain fields are exactly the same as in the usual first gradient model.To determine the components of the moment，we must first calculate the non-zero components of the gradient of the strain.Using the definition in Eq.（14），these components read

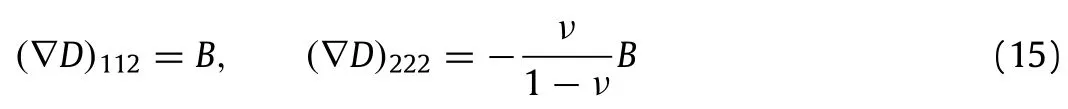
in Cartesian coordinates.In addition to the expressions of the gradient of the strain rate，use will be made of the relations

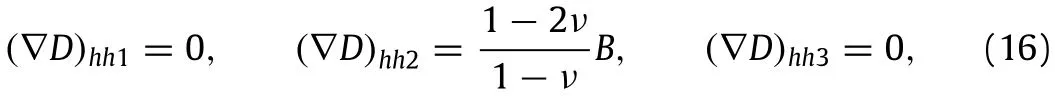
and

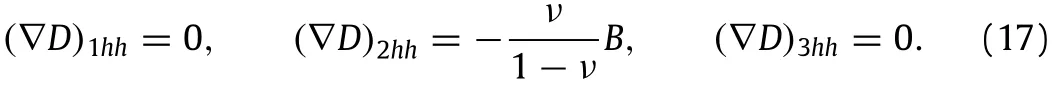
A combination of Eq.（6）（b）and the relations Eqs.（16）and（17）yields

We mustcheck that（1）the solution developed satisfies the balance equations and（2）it is possible to determine the displacement field using the components of the strain to assess the validity of the solution developed.We check the first requirement by expanding the balance equations（1）as

In the relation（19a），it only remainsΣ11，1−M112，12=0 which is satisfied since the stress and moment are independent of the coordinate X1.The relation（19b）is identically satisfied.It remains the relation（19c），i.e.，Σ33，3−M332，32=0，which is also satisfied because of the independence of the stress and moment fields with respect to the coordinate X3.

We can now address the second requirement.In the circular bending problem，the strain tensor is obtained as

Thus，to satisfy the second requirement，we must solve the system of equations

for the displacement component Ui.

The solution of the sub-equation（21a）reads

that of（21b）gives

and finally that of（21c）gives the ordinary differential equation

the solution of which reads

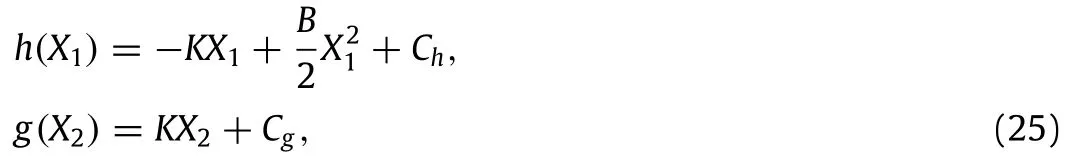
using a combination of the relations（22），（23）with the ordinary differential equation（24）.In the relation（25），Chand Cgare two unknown constants.In conclusion，the two requirements to check the validity of the solution developed are satisfied and this completes the developmentofthe solution ofthe firstproblem.The solution developed raises several points of interests.

All the required boundary conditions in Eq.（12）are satisfied，except for the condition on M222.Indeed，the component M222，defined by Eq.（18a），vanishes at±h only if the following criterionis met.This provides an interesting hint to determine the constitutive constants ci，which are related to the properties of the material.It also gives additional constraints on the boundary value problem considered in the study.A similar situation was encountered in Ref.［22］where an exact solution for the problem of a spherical shell obeying a purely GLPD micromorphic plasticity law was considered.The solution developed in the work of Enakoutsa［22］did not also meet all the required boundary conditions and this shortcoming was attributed to the fact that elasticity was not accounted for in the solution of the problem.

The other point of interest of the solution developed is that it can serve as reference solution to check the accuracy of the numerical implementation of a plasticity theory，which adopts the relations in Eq.（6）as hypoelasticity law.In fact，the solution of a closely related boundary value problem，considered in Refs.［15，16］，was used successfully to check the accuracy of a numerical algorithm developed by Enakoutsa［15，16］to implement into SYSTUS finite element code a constitutive model of ductile fracture incorporating the effects of the strain gradient.The good agreements obtained between the numerical predictions of the second-gradient plasticity model and the analytical solution have favored the applications of the model on several laboratoryoriented experiments.

Another point of interest concerns the strain rate field found. When the deformation of the beam occurs without volume change the Poisson ratio is equal toν=1/2.In fact，in this case tr D=0. Solving the equation defined by this condition forνusing the newly derived expression of the strain yield the condition uponν.If such is the case，the non-zero components of the moment tensor（M）reduce M112=2c4B and M222= −2（c4+c5）B.In addition，the conditions M222（±h）=0 enforce that c4= −c5.This reduces the five constitutive constants in the relation（6）to four.A good news when dealing with the characterization of these materials constants！

The second problem under consideration in this paper is the torsion of a non-circular cross-section beam.The displacement field in such a cylinder is classical and given by

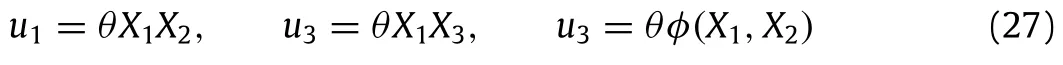
in an orthonormal coordinate system（O，e1，e2，e3）.In Eq.（27）the parameterθis the torsion angle and the functionφ，which depends on the variables X1，X2，is Saint Venant’s wrapping function.The non-zero components of the strain and its gradient are obtained from the displacement field（27）as

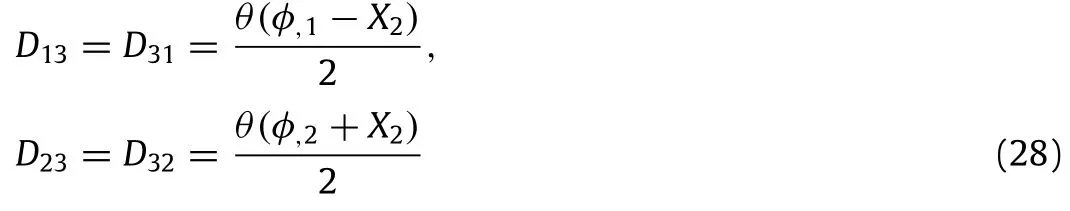
and

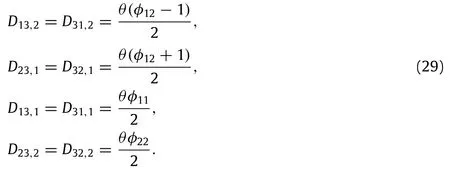
The non-zero components of the stress and the moment fields follow from the relations（6）as

where the symbolΔrepresents the mean in-plane Laplacian.The requirement for the stress and moment fields in Eqs.（30）and（31）to satisfy the balance equations（1）yields the following elliptic equation upon the wrapping functionφThe boundary conditions forφare found from substitution of Eqs.（30）and（31）in the boundary conditions（3）.They can be found in a complete formin Ref.［18］and partially in Ref.［23］.In the particular case where the effects of the microstructure are negligible（Δφ= 0）the boundary conditions for the wrapping function are given as

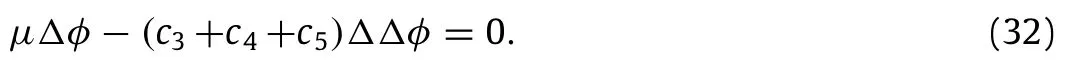
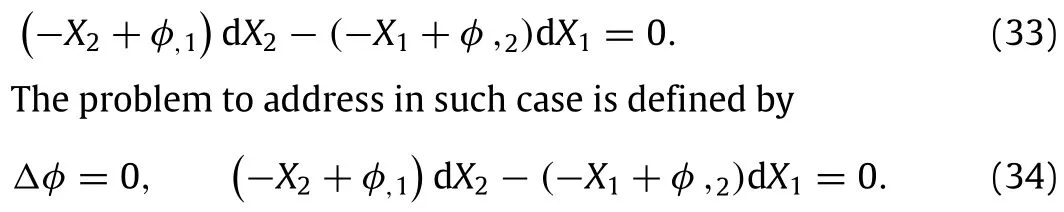
To solve Eq.（34），it is practical to introduce a functionψ，harmonic conjugate ofφsatisfying the following Cauchy conditions:

Using Cauchy’s conditions in Eq.（35），Eq.（33）is solved forψas

with cst being a constant independent of the coordinates X1，X2.

One of the major problems the new proposal raised is obviously the characterization of the constitutive constants that emerged. Two of these constants are the standard Lamé elasticity coefficients；it remains the five constitutive constants ci（1≤ i≤ 5）. They can be determined through a homogenization process where the material is idealized as being effectively homogeneous in a representative volume element（RVE）.The classical homogeneous conditions atthe boundary ofthe RVE is replaced by some inhomogeneous boundary conditions as proposed by Gologanu et al.［14］and Forest［24］and defined as

In Eq.（37），Eijkdenotes the components of the second gradient of the macroscopic displacement（Eijk=∇i∇jUk）and the gradient of the strain rate is related to E through formula

Assuming that the displacement field is of the form Eq.（37）everywhere in the RVE considered，not only on its boundary，the stress and moment fields associated with Eq.（37）are obtained as

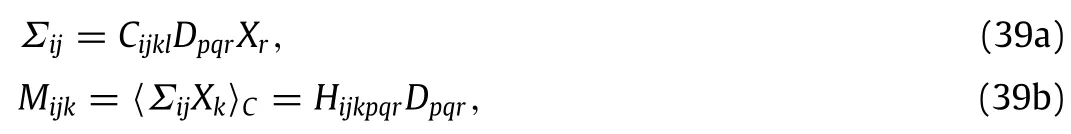
where the symbol‘‘〈·〉’’denotes the standard homogenization average formula，C is the RVE considered，Cijklare the components of the standard Hooke’s law 4th-rank elastic modulitensor，and Cijkpqrthe components of the 6th-rank tensor defined as

The constants ci（1≤i≤3）can be obtained by comparing the relations（39b）and（6）.A closely related method was used in Ref.［14］to determine the elastic moduli for an hypoelasticity law used to implement a model for ductile fracture including the effects of strain gradient.Analytical solutions for two problems，the bending of a circular beam under plane strain conditions and the torsion of a non-circular cross-section beam，the beams being made of a second-gradient isotropic elastic material，are provided in this study.The solution of the first problem was useful to establish some nice relationships between the unknown second-gradient elastic moduli，while the solution of the second one yields an elliptic problem on the wrapping function the solution of which is provided when second-gradient effects are negligible.Finally，a framework based on homogenization under inhomogeneous boundary strain rate conditions was suggested to find the unknown constants the new second-gradient elastic model involves.

［1］R.D.Mindlin，Microstructure in linear elasticity，Arch.Ration.Mech.Anal.12（1964）51-78.

［2］R.D.Mindlin，Second gradient of strain and surface-tension in linear elasticity，Int.J.Solids Struct.1（1965）417-738.

［3］E.Cosserat，F.Cosserat，Théorie des Corps Déformables，Hermann，Paris，1906（in French）.

［4］R.D.Mindlin，H.F.Tiersten，Effects of couple stresses in linear elasticity，Arch. Ration.Mech.Anal.11（1962）415-448.

［5］W.T.Koiter，Couple stress in the theory of elasticity I-II，Proc.Nederl.Akad. Wetensch.67（1964）17-44.

［6］R.Toupin，Elastic materials with couple-stresses，Arch.Ration.Mech.Anal.11（1962）385-414.

［7］A.E.Green，R.S.Rivlin，Multipolar continuum mechanics，Arch.Ration.Mech. Anal.17（1964）113-147.

［8］A.C.Eringen，Microcontinuum Field Theories I:Foundations and Solids，Springer-Verlang，New York，1999.

［9］A.C.Eringen，Vistas of nonlocal continuum physics，Internat.J.Engrg.Sci.30（1992）1551-1565.

［10］J.J.Alibert，P.Seppecher，F.DellIsola，Truss modular beams with deformation energy depending on higher displacement gradients，Math.Mech.Solids 8（2003）51-73.

［11］T.Bennett，I.M.Gitman，H.Askes，Elasticity theories with higher-order gradients of inertia and stiffness for the modelling of wave dispersion in laminates，Int.J.Fract.148（2003）185-193.

［12］I.Vardoulakis，G.Exakaktylos，S.K.Kourkoulis，Bending ofmarble with intrinsic length scales:a gradient theory with surface energy and size effects，J.Phys.IV Proc.8（1998）399-406.

［13］D.C.C.Lam，F.Yang，A.C.M.Chong，J.Wang，P.Tong，Experiments and theory in strain gradient elasticity，J.Mech.Phys.Solids 51（2003）1477-1508.

［14］M.Gologanu，J.B.Leblond，G.Perrin，J.Devaux，Recent extensions of Gurson’s model for porous ductile metals，in:P.Suquet（Ed.），in:Continuum Micromechanics，CISM Courses and Lectures，vol.377，Springer，Berlin，1997，pp.61-130.

［15］K.Enakoutsa，Modèle Non-locaux en Rupture Ductile des Métaux（Ph.Dthesis），Université Pierre et Marie Curie，Paris VI，2007（in French）.

［16］K.Enakoutsa，J.B.Leblond，Numerical implementation and assessment of the GLPD micromorphic model of ductile rupture，Eur.J.Mech.A-Solid 28（2009）445-460.

［17］K.Enakoutsa，A constitutive generalized elasticity law for GLPD micromorphic materials，with application to the problem of a spherical shell subjected to axisymmetric loading conditions，Theor.Appl.Mech.Lett.4（2014）021002.

［18］F.Dell’Isola，G.Sciarra，S.Vidoli，Generalized Hooke’s law for isotropic second gradient materials，Proc.R.Soc.A 465（2107）（2009）2177-2196.

［19］P.Germain，The method of virtual power in continuum mechanics.Part 2: Microstructure，SIAM J.Appl.Math.25（1973）556-575.

［20］X.L.Gao，S.Park，Variational formulation of a simplified strain gradient elasticity theory and its application to a pressurized thick-walled cylinder problem，Int.J.Solids Struct.44（2007）7486-7499.

［21］G.Maugin，Micromagnetism and polar media（Ph.D thesis），Princeton University，Princeton，1971.

［22］K.Enakoutsa，Exact results for the problem of a hollow sphere subjected to hydrostatic tension and made ofmicromorphic plastic porous materials，Mech. Res.Comm.49（2013）1-7.

［23］M.Sokolowski，Theory of Couple-Stresses in Bodies with Constrained Rotations，in:CISM Courses and Lectures，vol.26，Springer，Berlin，1970.

［24］S.Forest，Mechanics ofgeneralized continua:construction by homogenization，J.Physique IV 8（1998）39-48.

E-mail address：koffi@cavs.msstate.edu.

http://dx.doi.org/10.1016/j.taml.2015.04.002

2095-0349/©2015 Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

Beam

Analytical solution

*This article belongs to the Solid Mechanics