WKBJ analysis in the periodic wake of a cylinder

F.Giannetti

Department of Industrial Engineering，University of Salerno，84084 Fisciano（SA），Italy

WKBJ analysis in the periodic wake of a cylinder

F.Giannetti

Department of Industrial Engineering，University of Salerno，84084 Fisciano（SA），Italy

a r t i c l e i n f o

Article history：

Received 31 July 2014

Received in revised form

15 November 2014

Accepted 11 December 2014

Available online 9 March 2015

Cylinder wake

Secondary instability

Lagrangian trajectories

WKBJ approximation

The nature of the three-dimensional transition arising in the flow past a cylinder is investigated by applying the Lifschitz-Hameiri theory along special Lagrangian trajectories existing in its wake.Results show that the von Kármán street is unstable with regard to short-wavelength perturbations.The asymptotic analysis predicts the possible existence of both synchronous（as modes A and B）and asynchronous（as mode C）instabilities，each associated to specific Lagrangian orbits.The proposed study provides useful qualitative information on the origin of the different modes but no quantitative agreement between the growth rates predicted by the asymptotic analysis and by a global stability analysis is observed.The reasons for such mismatch are briefly discussed and possible improvements to the present analysis are suggested.

©2015 The Author.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

The flow in the wake of a two-dimensional cylinder becomes first unstable to three-dimensional disturbances at a Reynolds number（based on the free-stream velocity and the cylinder diameter）Re≈ 190.Experiments and numerical simulations have highlighted the presence of two different shedding modes with different spatial characteristics，generally referred to as modes A and B（see for examples in Refs.［1，2］）.Floquet analysis［3］certifies the existence of two separate bands of unstable modes:the first one（mode A）emerges for Re＞ 189 and has a spanwise wavelength of about 4 cylinder diameters，while the second one（mode B）appears for Re＞259 and is characterized by a shorter spanwise wavelength（about 0.8 diameter）.Both of them are synchronous modes，i.e.，they have the same periodicity of the base flow.An asynchronous quasi-periodic mode（usually termed mode C）with an intermediate wavelength also exists and was revealed by inserting in the flow a thin wire placed parallel to the cylinder axis（see Ref.［4］）.Depending on the geometry this mode can be stable（as in the case of a circular cylinder）or unstable（square cylinder and other geometries）.It is important to recall that the characteristics of the above mentioned modes and the associated transition scenarios are not specific to circular cylinders，but applies to a whole range of two-dimensional geometries ranging from square cylinders［5］to long plates with aerodynamic noses［6］.Despite the large number of experimental，theoretical and numerical studies performed on similar geometries，the precise nature of these modes is not fully understood yet.Several different mechanisms have been proposed to explain theirgenesis，including elliptic［7，8］，hyperbolic［7］，centrifugal［9］，or Benjamin-Feir［10］instabilities（see for instance in Ref.［11］for a detailed discussion）.However，no conclusive evidence supporting these speculations was given. In particular，a weak point of all these models consists in the fact that they are all based on idealized stationary flow configurations，while the real wake flow evolves in time and space in a complex way.

The scope of this letter is to illustrate an alternative approach to investigate the nature of the secondary instability which is based on the application ofthe Lifschitz and Hameiritheory［12，13］along particular orbits in the wake of the cylinder.The proposed analysis is an attempt to overcome the limitation of the previous theories bringing together results obtained through sensitivity analysis and asymptotic techniques.

Helpful information on the spatial and temporal evolution of the secondary instability can be retrieved by performing a structural sensitivity analysis of the unstable Floquet modes to localized force-velocity feedbacks，as proposed and explained in Refs.［14，15］.This procedure allows one to identify the instability core by inspecting the spatial structure of the instantaneous sensitivity tensor

where u and f+are respectively the direct and adjoint Floquet eigenvectors and k is the wavenumber in the periodic direction. By plotting its spectral norm，it is possible to trace the spatial and temporal evolution of the instability core during the phases of the vortex shedding.Results for mode A and mode B show that the instability is very localized in space and evolves in times in a com-plex way（see Ref.［14］for details）.Preliminary results obtained on a square cylinder at Re=205 presents similar characteristics for all unstable modes.Moreover as noticed by Camarri and Giannetti［14］，in the wake of the cylinder there exist closed Lagrangian trajectories，i.e.，orbits described by materialpoints which return to theirinitialposition aftera shedding cycle.Such orbits are solutions of the ordinary differential equation（o.d.e.）

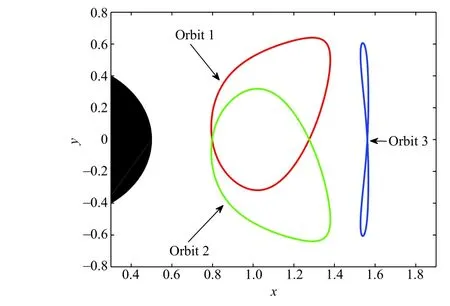
Fig.1.Numbering of the closed orbits existing in the wake of a cylinder at Re= 260.

In these expressions X ≡ ｛xo，yo｝indicates the coordinates of the material points lying along the Lagrangian trajectory，Ubis the periodic base flow and T is the shedding period.Here we used a fourth-order Runge-Kutta scheme coupled to a Newton-Raphson procedure to solve Eqs.（2）and（3），while the base flow was determined with the same finite-difference immersed boundary code described in Ref.［14］.The analysis was performed for both circular and square cylinders（not documented here for sake of brevity）: in both cases we found three closed Lagrangian trajectories with shapes and symmetries similar to those depicted in Fig.1.For the sake of precision，we have to say that there are actually an infinity of closed orbits satisfying Eq.（2）but on which a material point comes back to its initial position after n＞ 1 shedding periods. These solutions，however，are not considered in the present letter and are left for future investigations.The sensitivity analysis reveals that the instability core for modes A and B is highly localized in space:the highest sensitivity regions strictly follow the position of the material points moving along the closed orbits，showing the existence of a strong correlation between these orbits and the instability core.An example of such behavior is reported in Fig.2，where the temporal evolution of the points on the closed orbits are depicted for mode B（at Re=260）together with the spectral norm of the sensitivity tensor I（x，y，k，t）during a whole shedding period.Similar conclusions hold for the unstable modes arising in the wake of a square cylinder.

The strong localization of the instability core revealed by the structural sensitivity analysis suggests the possibility to use a‘‘local theory’’to describe its generation and evolution.An appealing approach in this context is given by the short-wavelength（WKBJ）approximation introduced by Lifschitz and Hameiri［12，13］.Here，the solution of the linearized Navier-Stokes equations is sought in the formofa rapidly oscillating and localized wave-packetevolving along a Lagrangian trajectory X（t）and characterized by a wavevector k（t）=∇φ（x，t）and an envelope a（x，t）such that

Table 1 Eigenvalues of the fundamental Floquet matrix associated to Eq.（5）for the three closed orbits.See Fig.1 for the orbit numbering.

withϵ≪1.In the limit of vanishing viscosity（Re→0）and large wavenumbers（∥k∥→∞），the theory enables one to evaluate，at leading order，the growth rate associated with a localized perturbation.This is achieved by solving the following set of linear o.d.e.

along the Lagrangian trajectories satisfying Eq.（2）with some initial conditions.In the previous equations L=∇Ubis the velocity gradient tensor of the base flow，I is the identity tensor and the superscript‘‘t’’indicates the transpose operator.

As proved by Lifschitz and Hameir［12，13］，inviscid instability occurs when such system has at least one solution with∥a（t）∥→∞as t→∞.This theory has been successfully applied in the past to study centrifugal，elliptic and hyperbolic instabilities developing on 2D steady base flows（see for examples［16-22］）.In order to characterize the instability mechanism occurring in the periodic wake of the cylinder using such local theory，however，the selfexcited nature of the instability must be properly accounted for.In such context，a central role is played by the closed Lagrangian trajectories described in the previous section.Such trajectories might play a special role in the dynamics of the instability:from an inviscid point of view，in fact，local instability waves might propagate on the closed orbits and feedback on themselves leading to a selfexcited mode.

In order to apply the theory，both Eqs.（5）and（6）must be integrated along the three closed trajectories found in the wake. Since the base flow is periodic，Eq.（5）is a linearo.d.e.with periodic coefficients whose general solution can be written in terms of Floquet modes.In particular，the solution can be found by building the fundamental Floquet matrix M（T），solution of the system

and extracting its eigenvalues and the corresponding eigenvectors. Using these eigenvectors as initial conditions to integrate Eq.（5），it is possible to retrieve the temporal evolution of k during a whole shedding cycle.Equation（5）admits three independent solutions related to the three eigenvectors of the fundamental Floquet matrix M（T）.The corresponding eigenvaluesµfor both Re=190 and Re=260 are listed in Table 1.Since the base flow is periodic and 2D，for each orbitthere exists an eigenvalue equalto 1 with a corresponding eigenvector which remains constant in time and perpendicular to the base flow.The other two eigenvectors，instead，lie in the same plane as the base flow and are associated with a complex conjugate pair of eigenvalues.

Once Eq.（5）is solved，the amplitude a can be found by integrating Eq.（6）.In principle，to set k in Eq.（6），we can use a general linear combination of the Floquet modes previously determined. However，since we are trying to determine a self-excited mode，we only consider solutions of Eq.（5）which are periodic in time，i.e.，solutions such that k（0）=k（T）.Therefore，only the constant eigenvector orthogonal to the base flow k=kˆz（associated

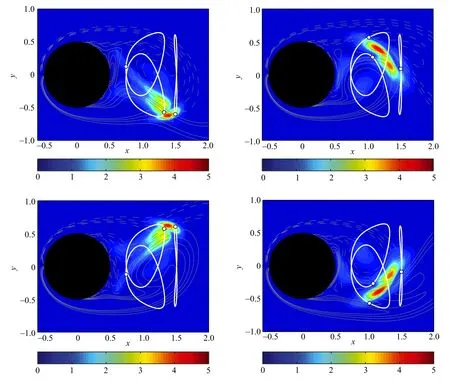
Fig.2.Closed Lagrangian orbits in the periodic wake behind a circular cylinder at Re=260:the position of the material points（small circles）along the closed orbits（white lines）is shown for the four phases（0，π/4，2π/4，3π/4）in which the shedding cycle has been divided.The spectral norm of the tensor I（x，y，t，k）is also superposed（mode B at k=7.64）.

with the eigenvalue 1）has to be considered.Solutions of Eq.（6）associated with an orthogonal k are usually termed‘‘pressureless modes’’.With this choice，Eq.（6）is again an ordinary linear differential equation with periodic coefficients.According to Floquet theory，its solution can be written in terms of Floquet modes

where¯a（t）is a T periodic function andσis the growth rate of the perturbation.In order to make a quantitative comparison with the growth rates predicted by the global analysis，we have computed the values ofσin Eq.（9）for the 3 closed orbits.As for Eq.（5），the fundamental Floquet matrix A corresponding to Eq.（6）is built by integrating the system

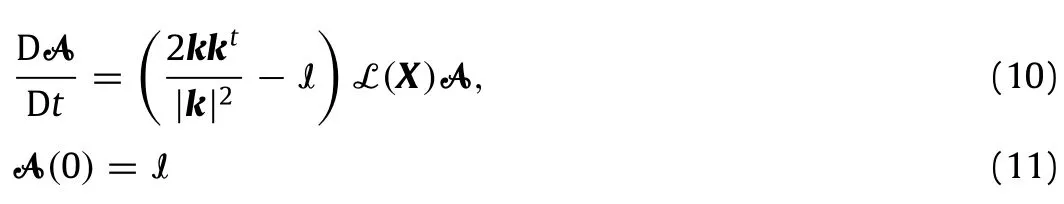
along each orbit.The eigenvaluesµand the corresponding eigenvectors of A（T）are then easily extracted.

Since the base flow is 2D and the wavevector k is orthogonal to the base flow plane，we expect that one eigenvalue of A is 1. The others two，for the incompressibility constrain，must multiply to 1，i.e.，µ1µ2=1.The Floquet exponentsσare related to the eigenvaluesµof A（Floquet multipliers）by the simple relation

where T is the period of the base flow.The Floquet exponents for the three orbits and the corresponding eigenvaluesµof the fundamental Floquet matrix are reported in Table 2，both for Re= 190 and for Re=260.

According to these results the periodic wake behind the cylinder is highly unstable with regard to short-wavelength perturbations.A parametric analysis on a limited number of configurations has been performed in order to better understand the effects ofthe base-flow Reynolds number on the instability.At leading order the theory is purely inviscid and viscous effects enter only through the modification ofthe base-flow characteristics（velocity gradient，shape of the closed orbits and value of the shedding period T）.Results show that the flow gets more and more unstable as the baseflow Reynolds number is increased.Note also that the asymptotic analysis predicts the presence of both synchronous instabilities（as modes Aand B）arising along orbitno.3 and asynchronous instabilities（as mode C）growing on orbits nos.1 and 2.The considered orbits，thus，are sufficient to qualitatively justify the existence of the different kind of modes observed in the wake behind 2D cylinders. Note also that the asynchronous modes come in pairs and are associated to two different orbits，mimicking the fact that in a global analysis mode C is associated to a complex conjugate pair of eigenvalues.On the otherhand，in a globalframework，modes Aand Bare always associated to realFloquetexponents and are therefore compatible only with instabilities arising on orbit no.3.Note that the growth rates predicted by the asymptotic theory are not in quantitative agreementwith those obtained by a fullglobalstability analysis（see data reported in Table 3 for a short summary）.A similar conclusion was also found by Gallaire et al.［21］who applied theLifschitz and Hameiri theory to the transverse global instability of a detached boundary layer.

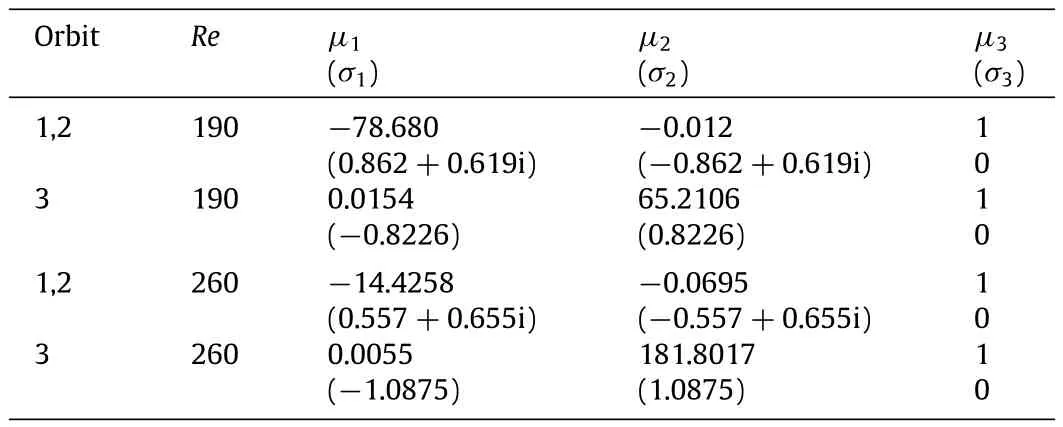
Table 2 Floquet multipliersµassociated to Eq.（6）and the corresponding Floquetexponents σfor the three closed orbits.See Fig.1 for the orbit numbering.

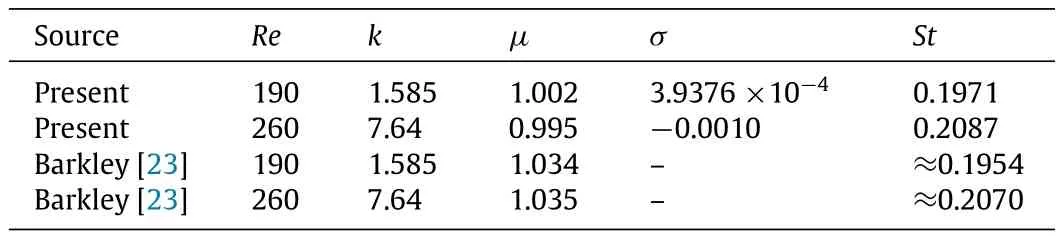
Table 3 Floquet multipliersµand exponentsσfor mode A（Re= 190）and mode B（Re=260）predicted by the global stability computations performed in the present analysis and in Ref.［23］.

One possible explanation for such disagreementcan be found in the lack of finite Reynolds-number and finite-wavenumber effects，not accounted by the leading order approximation.Recall，in fact，that Eqs.（5）and（6）provide an estimate ofthe perturbation growth rate in the limit of vanishing viscosity and infinite wavenumber. Considering that for the flow investigated here Re is only moderately large and that the wavenumber k corresponding to the maximum amplification is justslightly larger than 1，such disagreement is not really surprising.

Although the results obtained by the application of the asymptotic theory are not quantitatively correct，they provide valuable information that can be further used to disclose the role of the closed orbits in the development of the secondary instability.The results discussed in this lettersuggestthatorbitno.3 is responsible for the generation of synchronous instabilities，like modes A and B，while orbits no.1 and no.2 are associated to the existence of asynchronous instabilities，like mode C.In principle，a more satisfactory agreement between the global and the asymptotic analysis might be achieved by considering correction terms due to viscous and finite wavenumber effects.Landman and Saffman［24］introduced in Eqs.（5）and（6）a term accounting for the viscous dissipation:such correction depends on both Re and|k|in a way to produce larger attenuation for modes with smaller spanwise wavelengths.For the circular cylinder case，results show that for mode A at Re=190 and k=1.585 and for mode B at Re=260 and k=7.64 the Floquet multiplierµ2on orbit no.3 is reduced respectively by 6.5% and 65.5%compared to its inviscid values reported in Table 2.The resulting growth rates，however，are still too large if compared with those obtained by the global analysis.Larger corrections to the growth rate could result from finite-wavenumber effects not considered here.Bayly［16］pointed outthatfor2Dstationary flows with closed streamlines itis possible to constructan inviscid global mode of finite wavenumber along the most unstable closed orbit. Using such theory，Citro etal.［22］studied the transverse instability arising in open cavities and showed that only considering finitewavenumber corrections，the asymptotic theory is able to provide results in quantitative agreement with the global analysis. For periodic flows，however，a‘‘local theory’’accounting for finitewavenumber effects and linking the characteristics of the closed Lagrangian trajectories with the global spatial features of the selfsustained mode is still lacking.

For this reason further tests are necessary to better clarify the role of both viscosity and wavenumber on the localization of the instability.In principle this can be achieved by freezing the base flow ata given Reynolds number and then repeating the sensitivity analysis while progressively increasing Re and k in the linearized equations only.Preliminary results on the cylinderwake show that，as k and Re get larger，the instantaneous sensitivity for mode B tends to focus closer and closer to the Lagrangian point moving on orbit 3，partially confirming the results presented in this paper. Similar tests could provide further information on the possibility to develop a complete local theory of the secondary instability.

The author is grateful to Professor P.Luchini and Professor S.Camarri for their valuable comments and advices.

［1］C.H.K.Williamson，The existence of two stages in the transition to threedimensionality of a cylinder wake，Phys.Fluids 31（1988）3165-3168.

［2］C.H.K.Williamson，Vortex dynamics in the cylinder wake，Annu.Rev.Fluid Mech.28（1996）477-539.

［3］D.Barkley，R.D.Henderson，Three-dimensionalFloquetstability analysis ofthe wake of a circular cylinder，J.Fluid Mech.322（1996）215-241.

［4］H.Q.Zhang，U.F.Fey，B.R.Noack，On the transition of the cylinder wake，Phys. Fluids 7（1995）779-794.

［5］J.Robichaux，S.Balachandar，S.Vanka，Three-dimensional Floquet instability of the wake of square cylinder，Phys.Fluids 11（1999）560-578.

［6］K.Hourigan，M.Thompson，B.Tan，Self-sustained oscillations in flows around long blunt plates，J.Fluids Struct.15（2001）387-398.

［7］C.H.K.Williamson，Three-dimensional wake transition，J.Fluid Mech.328（1996）345-407.

［8］T.Leweke，C.H.K.Williamson，Three-dimensional instabilities in wake transition，Eur.J.Mech.B Fluids 17（1998）571-586.

［9］M.Brede，H.Eckelmann，D.Rockwell，On secondary vortices in a cylinderwake，Phys.Fluids 8（1996）2117-2124.

［10］T.Leweke，M.Provansal，The flow behind rings:bluff body wakes without end effects，J.Fluid Mech.288（1995）265-310.

［11］M.C.Thompson，T.Leweke，C.H.K.Williamson，The physical mechanism of transition in bluff body wakes，J.Fluids Struct.15（2001）607-616.

［12］A.Lifschitz，E.Hameiri，Localstability conditions in fluid dynamics，Phys.Fluids 3（1991）2644-2651.

［13］A.Lifschitz，Short wavelength instabilities of incompressible threedimensional flows and generation of vorticity，Phys.Lett.A 157（1991）481-487.

［14］S.Camarri，F.Giannetti，Effect of confinement on three-dimensional stability in the wake of a circular cylinder，J.Fluid Mech.642（2010）477-487.

［15］P.Luchini，F.Giannetti，J.O.Pralits，in:Proocedings of the 5th AIAA Theoretical Fluid Mechanics Conference，23-26 June，Seattle，Washington，USA，2008，AIAA paper AIAA-2008-4227.

［16］B.J.Bayly，Three-dimensional centrifugal-type instabilities in inviscid twodimensional flows，Phys.Fluids 31（1988）56-64.

［17］D.Sipp，L.Jacquin，Elliptic instability in two-dimensional flattened Taylor-Green vortices，Phys.Fluids 10（1998）839-849.

［18］D.Sipp，E.Lauga，L.Jacquin，Vortices in rotating systems:centrifugal，elliptic and hyperbolic type instabilities，Phys.Fluids 11（1999）3716-3728.

［19］S.Leblanc，C.Cambon，Effects of the Coriolis force on the stability of Stuart vortices，J.Fluid Mech.356（1998）353-379.

［20］C.P.Caulfield，R.R.Kerswell，The nonlinear development of three-dimensional disturbances at hyperbolic stagnation points:A model of the braid region in mixing layers，Phys.Fluids 12（2000）1032-1043.

［21］F.Gallaire，M.Marquillie，U.Ehrenstein，Sensitivity analysis and passive control of cylinder flow，J.Fluid Mech.571（2008）221-233.

［22］V.Citro，F.Giannetti，L.Brandt，P.Luchini，Linear three-dimensional global and asymptotic stability analysis of incompressible open cavity flow，J.Fluid Mech. 768（2015）113-140.

［23］D.Barkley，Confined three-dimensional stability analysis of the cylinder wake，Phys.Rev.E 71（2005）017301.

［24］M.J.Landman，P.G.Saffman，The three-dimensional instability of strained vortices in a viscous fluid，Phys.Fluids 30（1987）2339-2342.

E-mail address：fgiannetti@unisa.it.

http://dx.doi.org/10.1016/j.taml.2015.03.001

2095-0349/©2015 The Author.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

*This article belongs to the Fluid Mechanics