Linear global stability of a confined plume

Lutz Lesshafft

Laboratoire d'Hydrodynamique，CNRS-École polytechnique，Palaiseau，France

Linear global stability of a confined plume

Lutz Lesshafft

Laboratoire d'Hydrodynamique，CNRS-École polytechnique，Palaiseau，France

a r t i c l e i n f o

Article history：

Received 19 July 2014

Received in revised form

7 January 2015

Accepted 2 February 2015

Available online 8 May 2015

Plume

Linear instability

Laminar flow stability

Buoyancy-driven instability

Bifurcation and symmetry breaking

A linear stability analysis is performed for a plume flow inside a cylinder of aspect ratio 1.The configuration is identical to that used by Lopez and Marques（2013）for their direct numerical simulation study. It is found that the first bifurcation，which leads to a periodic axisymmetric flow state，is accurately predicted by linear analysis:both the critical Rayleigh number and the global frequency are consistent with the reported DNS results.It is further shown that pressure feedback drives the global mode，rather than absolute instability.

©2015 The Author.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

Localized heating on a horizontal surface entrains a buoyancydriven plume flow in the fluid above.Plumes are very common in the oceans and in the atmosphere，and they are of great importance to transport and mixing processes［1］.Unconfined by fluid boundaries or by strong stratification，plumes represent a class of open shear flows.Plumes within a confined geometry represent a closed flow，which is likely to induce marked differences in the dynamics when compared to unconfined situations.Confined plumes are notably encountered in internalventilation problems［2］and in Rayleigh-Bénard convection［3］.

Lopez and Marques［4］used direct numerical simulation（DNS）for a comprehensive investigation of the dynamics of confined plumes.Their study describes several successive bifurcations，associated with symmetry breaking，for what is arguably the most basic confined plume configuration:the internal flow in a fluidfilled cylinder，induced by localized heating at the bottom wall.As the wall heating becomes more and more intense，characterized by an increasing value of the Rayleigh number，steady convection becomes dominant over diffusion for the heat transport.Beyond a firstcriticalRayleigh number，the steady plume flow bifurcates to a time-periodic regime，characterized by the convection of axisymmetric‘‘puffs’’along the centerline of the plume.The next bifurcation，at a higher critical value of the Rayleigh number，leads to a breaking ofthe axialsymmetry，and furthersuccessive bifurcations lead to chaotic flow states and eventually to turbulence.

The present paper aims to investigate the first bifurcation，from a steady flow to a time-periodic limit cycle，using the tools of linear global stability analysis.Lopez and Marques describe this transition as a supercritical Hopf bifurcation，which suggests that the observed nonlinear dynamics are related to the destabilization of a linear temporal eigenmode of the steady-state system.The flow geometry as well as the governing equations are chosen exactly identical to the standard configuration in the reference DNS:the fluid is confined in a vertical cylinder of height and diameter both equal to 1.All walls are isothermal，at a constant temperature T0−ΔT/2，exceptatthe bottomwall，where a circular spot of radius rdis heated to a temperature T0+ΔT/2.The wall temperature varies smoothly over the radial distance[rd，rd+rw] from the cylinder axis，according to expression（2.5）of Ref.［4］. As in the reference study，we choose rd= rw= 0.125.The nondimensional wall temperature is 0.5 in the center of the hot spot，and−0.5 everywhere outside the heated area.

The governing equations are cast in the Boussinesq approximation，written in nondimensional form identically to Ref.［4］as

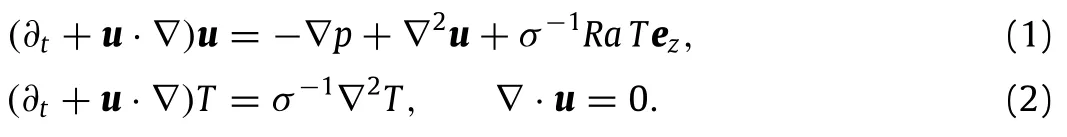
The nondimensional parameters of the problem are the Rayleigh number Ra= αgd3ΔTκ−1ν−1and the Prandtl number σ = ν/κ.All symbols are standard notation（see Ref.［4］）.The Rayleigh number is proportional to the dimensional temperature difference，and may be interpreted as representing the intensity of the heating.

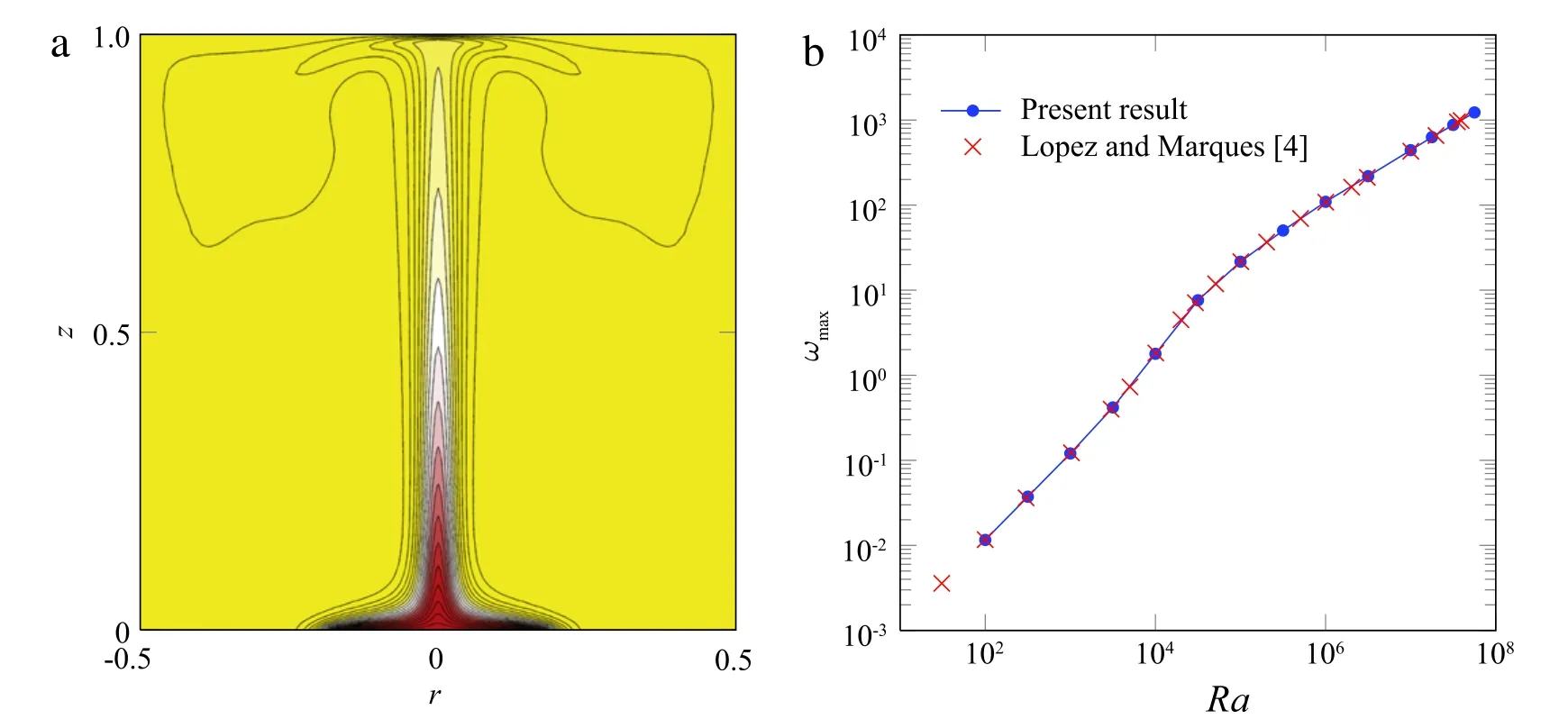
Fig.1.（Color online）（a）Temperature distribution in the steady base flow at Ra=107.Twenty contour levels between Tmin=−0.5 and Tmax=0.5 are shown.（b）Maximum vertical velocity wmaxof the steady base flow，as a function of Rayleigh number.Blue line and dots:present results；red crosses:results reported by Lopez and Marques［4］，rescaled by a factorσ=7.

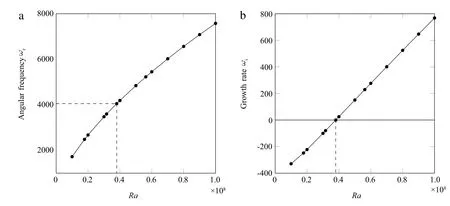
Fig.2.Linear instability eigenvalue as a function of Rayleigh number.（a）Angular frequency（real part）.（b）Temporal growth rate（imaginary part）.

In a first step，base flow states are computed as exact steady solutions of the nonlinear equations（1）and（2）.In a second step，the same equations are linearized around the base flow，and temporal eigenmodes of this linear system are extracted.Both numerical procedures are performed using a finite element method as implemented in the FreeFEM++package（http://www.freefem.org）.A Newton-Raphson method is employed to identify the steady base flow for a given setting ofσand Ra.All results presented herein pertain toσ=7，consistent with the standard case of Ref.［4］.The temperature distribution of the base flow at Ra=107is represented in Fig.1（a）.It appears to be indeed identical to the result of Lopez and Marques［4］（their Fig.3（a），same colormap）.The associated velocity fields are also consistent，provided that the values reported in Ref.［4］are divided by the Prandtl number，σ=7，as plotted in Fig.1（b）.Itseems thatthe time scaling in Ref.［4］is based on thermaldiffusivity，whereas a viscous scale is used here.The accuracy of the present base flow results has been verified through independenttime-resolved simulations with the software package Gerris［5］.

Temporal eigenmodes of the linearized form of Eqs.（1）and（2）are sought in the form u′（r，θ，z，t）= ˆu（r，z）exp（i mθ−iωt），and accordingly for perturbations T′and p′.The eigenvalue is the complex frequencyω=ωr+iωi，whereωirepresents the temporal growth rate.It is found that all eigenmodes are stable（ωi＜ 0）at Rayleigh numbers below the critical value Rac=3.801×107. At Rayleigh numbers Ra ＞ Rac，one axisymmetric instability mode（m=0）becomes unstable，while helical modes（|m|≥1）remain stable at least up to Ra= 108.The angular frequency and growth rate of this unstable global mode are displayed as functions of Rayleigh number in Fig.2.The critical value for onset of linear global instability is to be compared to the value reported in Ref.［4］，Ra=3.854×107，at which self-excited axisymmetric perturbations are observed in the nonlinear simulations.The global angular frequency of the limit cycle in the simulations is approximately˜ωg=28500 in terms of the diffusive time scale，orωg= ˜ωg/σ ≈ 4070 when rescaled to the viscous time scale used in the present study.This latter value matches within 0.5% accuracy the frequencyωr=4050 that linear instability analysis predicts at the critical Rayleigh number（see Fig.2（a））.

Lopez and Marques［4］point out that the oscillation period of the nonlinear limit cycle corresponds to the propagation time of a vortex ring along the axis of the plume.The vortex then impacts the top wall，causing a pressure perturbation，which in turn triggers the formation of a new vortex ring near the bottom wall.Al-though the roll-up of a vortex ring is a strongly nonlinear event，it is remarkable how the linear eigenmode reproduces the same qualitative behavior.Figure 3（a）displays the linear temperature perturbation at one instance during the cycle.It resembles very much the nonlinear snapshots shown in Fig.10 of Ref.［4］.The propagation time of disturbances is visualized in the space-time diagram in Fig.3（b），which shows pressure perturbations along the vertical z，at a fixed radial station r=0.1，as a function of time. A pressure maximum（minimum）near the top wall coincides precisely with a maximum（minimum）atthe bottom wall，which then propagates upward.The picture suggests the presence of a pressure feedback，similar to what is observed for instance in cavity flows［6］.Figure 3（c）finally shows the structural sensitivity of the unstable eigenmode，in the sense of Giannetti and Luchini［7］.This quantity is computed as the local product of the norms of the direct eigenfunction and its adjoint.The structural sensitivity of the unstable eigenmode is seen to be significant only in the vicinity of the hot spot near the bottom wall.This observation suggests that this flow region is of particular importance for the destabilization of the eigenmode.It is plausible that the strong pressure fluctuations generated at the top boundary，where the vorticity impinges on the wall，induce perturbations in the receptive flow region near the hot spot at the bottom.Synchronized communication between these two flow regions establishes a feedback loop that seems to be the root cause for the observed instability.

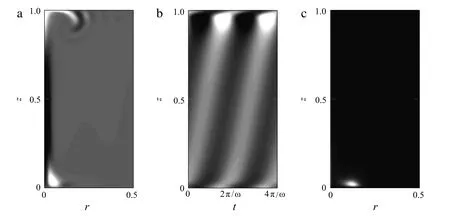
Fig.3.Linear perturbation eigenfunctions of the unstable mode at the critical Rayleigh number Ra=3.801×107.（a）Temperature perturbation（snapshot）.（b）Pressure perturbation at r=0.1 as a function of z and time.Two oscillation periods are shown.（c）Structural sensitivity.White is positive，black is negative（or zero in plot（c））.

It is classically assumed that global instability may either be linked to pressure feedback，as described here，or to the presence oflocalabsolute instability［8］.A localanalysis has been performed forthe base flow atthe criticalsetting Ra=3.801×107，confirming that the flow at this setting is convectively unstable everywhere. Absolute instability therefore does not provide the global instability mechanism.All these observations support the interpretation that the vertical confinement leads to pressure feedback that induces a global instability.It is remarkable that such a seemingly nonlinear scenario is captured with high quantitative accuracy by a linear analysis.

Acknowledgments

The author sincerely thanks Gaétan Lerisson at LadHyX for his generous help with the Gerris simulations.Financial support for this work was provided by the Agence Nationale de la Recherche under the‘‘Cool Jazz’’project.

［1］P.Linden，Convection in the environment，in:Perspectives in Fluid Dynamics: A Collective Introduction to Current Research，2000，pp.289-345.

［2］P.Linden，The fluid mechanics of natural ventilation，Annu.Rev.Fluid Mech.31（1999）201-238.http://dx.doi.org/10.1146/annurev.fluid.31.1.201.

［3］S.Grossmann，D.Lohse，Fluctuations in turbulent Rayleigh-Bénard convection: the role of plumes，Phys.Fluids 16（2004）4462-4472.http://dx.doi.org/10. 1063/1.1807751.

［4］J.M.Lopez，F.Marques，Instability of plumes driven by localized heating，J.Fluid Mech.736（2013）616-640.http://dx.doi.org/10.1017/jfm.2013.537.

［5］S.Popinet，Gerris:a tree-based adaptive solver for the incompressible Euler equations in complex geometries，J.Comput.Phys.190（2003）572-600. http://dx.doi.org/10.1016/S0021-9991（03）00298-5.

［6］E.Åkervik，J.Hœpffner，U.Ehrenstein，D.Henningson，Optimal growth，model reduction and control in a separated boundary-layer flow using global eigenmodes，J.Fluid Mech.579（2007）305-314.http://dx.doi.org/10.1017/ S0022112007005496.

［7］F.Giannetti，P.Luchini，Structural sensitivity of the first instability of the cylinder wake，J.Fluid Mech.581（2007）167-197.http://dx.doi.org/10.1017/ S0022112007005654.

［8］P.Huerre，P.Monkewitz，Local and global instabilities in spatially developing flows，Annu.Rev.Fluid Mech.22（1990）473-537.http://dx.doi.org/10.1146/ annurev.fl.22.010190.002353.

E-mail address：lutz.lesshafft@ladhyx.polytechnique.fr.

http://dx.doi.org/10.1016/j.taml.2015.05.001

2095-0349/©2015 The Author.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

*This article belongs to the Fluid Mechanics