基于幂函数的修形齿轮建模与仿真*

马元节，周金宇，丁前进，王礼明，李朴义

（1.江苏理工学院装备再制造工程高技术重点实验室，江苏常州 213001；2.同济大学软件学院，上海 200092）

基于幂函数的修形齿轮建模与仿真*

马元节1，周金宇1，丁前进2，王礼明1，李朴义1

（1.江苏理工学院装备再制造工程高技术重点实验室，江苏常州 213001；2.同济大学软件学院，上海 200092）

近年来齿轮传动机构朝着高速、重载、高效的方向发展，这一趋势对齿轮提出了高稳定性、高可靠性、低噪音等要求。针对该要求提出基于幂函数的齿廓修形方法并完成基于幂函数的齿廓修形齿轮的参数化几何建模。为提高齿轮传动的仿真分析效率和精度，联合运用MATLAB与脚本语言Python在ABAQUS环境下对齿轮传动有限元分析模型进行二次开发，实现齿轮动态啮合分析从建模到后处理的参数化流程。通过实例分析相同转速下修形前后齿轮传动的动态啮合性能，结合理论分析验证了分析流程的准确性与高效性，为齿轮传动的动态设计奠定理论基础、提供可行方法。

轮齿修形；参数化；幂函数；Matlab；Abaqus

0 引言

齿轮传动机构是机械传动中应用最为广泛的传动机构之一，具有传动平稳、可靠、效率高、寿命长等优点。目前齿轮传动正在朝高速、重载、高效的方向发展，这一发展趋势对齿轮本身的稳定性、可靠性等提出严格要求。大量的理论研究与实践论证表明：正确合理的齿廓修形能够改善齿轮的载荷分布，降低振动与噪声，提高齿轮的承载能力以及疲劳寿命。因此，齿廓修形对于高速重载齿轮而言是不可或缺的技术之一。

近年来，随着虚拟样机技术和有限元方法的不断发展，其在齿轮设计和分析领域得到了较为广泛的应用。齿轮动态啮合问题是一个边界条件高度非线性的接触动力学问题。ABAQUS作为国际上最为先进的有限元分析软件之一，为齿轮动态啮合分析提供了必要的软件条件。然而目前通过有限元方法分析齿轮接触性能大多采用静态接触分析的方法，由于该方法忽略了结构本身的惯性，所以对齿轮啮合过程仿真并不十分准确［1-2］。同时，对于齿轮的啮合分析大多采用传统的CAE界面，更多的步骤是通过手工操作来实现，繁琐的手工操作大大降低了分析效率。在结果处理上，传统分析往往不能够满足需求或者结果数据量太大，并且容易造成数据丢失。因此，有必要借助ABAQUS的脚本语言Python对齿轮动态接触分析模型进行二次开发。本文联合数据处理能力非常强大的数学软件MATLAB和能够操纵ABAQUS内核的脚本语言Python对齿轮动态啮合分析有限元模型进行二次开发，开发出了齿轮动态啮合仿真平台，实现了从建模到后处理的自动化流程，大大地提高了分析效率。

1 基于幂函数的修形齿轮几何建模

齿轮在进入和退出啮合过程中，由于主动齿轮实际基节与从动齿轮实际基节不相等的原因，造成了齿轮在啮入或啮出时出现冲击现象。针对这一现象，本文提出以满足幂函数规律的修形曲线代替标准渐开线齿轮齿顶部位的局部齿形线，形成由渐开线与满足幂函数规律的修形曲线组合而成的新齿廓曲线，进而形成一种全新的修形齿轮。

考虑到齿轮建模过程中绘制公式曲线必须在直角坐标系下进行，因此建模的关键在于确定齿轮齿廓曲线上每一点的坐标值。

如图1所示，完整的齿廓曲线由标准渐开线BO'和修形曲线O'D两部分组成，其中B为基圆上某一点，O'为修形起点，而基于幂函数的修形曲线是在给定修形指数n、修形长度L和最大修形量Δ（即图1中圆弧AD）的情况下所确定的修形曲线，并且修形曲线所满足的幂函数规律如下：

因此，确定未知的修形系数a就成为了解决问题的核心所在。

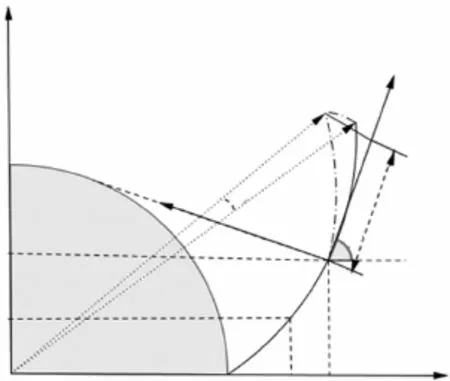
图1 修形坐标示意图

1.1 直角坐标系下渐开线方程

如图1所示，以齿轮中心为原点O，过渐开线起点B与原点O的直线为横轴建立如图所示的全局直角坐标系XOY。渐开线上任意一点K在直角坐标系XOY中的坐标［3］表达式为：

式中xk-渐开线上任意一点K在直角坐标系XOY下的横坐标；

yk-渐开线上任意一点K在直角坐标系XOY下的纵坐标；

φk-渐开线上任意一点K处的滚动角；

φ'k-渐开线上任意一点K处的滚动角所对应弧度值。

考虑到该方程中的滚动角在齿轮设计过程中不便引用，因此结合标准渐开线极坐标方程，建立以渐开线上任意一点处压力角为参数的渐开线方程：

1.2 修形系数推导

由于修形参数数值大小无法与齿轮整体尺寸相比拟，为了使计算出修形系数a的数值大小可观，因此以修形起点O'为原点，过O'且与齿轮基圆相切于N'点的直线为纵轴建立如图所示的局部直角坐标系X'O' Y'，其中AB为渐开线，O'D为修形曲线，L为修形长度，圆弧AD为最大修形量。

由于修形曲线函数上的点均是针对局部坐标系X'O'Y'而言，因此需要在全局坐标系XOY中，将A点绕齿轮中心O点旋转以最大修形量为弧长的圆弧AD所对应的圆心角θ至D点，再将D点全局坐标通过坐标变换变换至局部坐标系X'O'Y'中得出D点的局部坐标。

式中D-D点局部坐标矩阵；

x'D-修形曲线终点D在局部直角坐标系X'O'Y'下横坐标；

y'D-修形曲线终点D在局部直角坐标系X'O'Y'下纵坐标；

A-A点全局坐标矩阵；

xA-渐开线上A点在全局坐标系XOY中的横坐标；

yA-渐开线上A点在全局坐标系XOY中的纵坐标；

M-全局坐标系XOY下A点旋转至D点的变换矩阵；

N-全局坐标系XOY下D点变换至局部坐标系X'O'Y'下的D'点的变换矩阵；

θ-齿顶圆弧上弧长为最大修形量时所对应圆弧的圆心角；

α-局部坐标系X'O'Y'相对于全局坐标系XOY的旋转角度；

x'0-局部坐标系原点O'在全局坐标中的横坐标；

y'0-局部坐标系原点O'在全局坐标中的纵坐标。

修形系数a求解公式：

至此，修形曲线上每一点局部坐标被完全确定，再将修形曲线上每一点局部坐标变换至全局坐标系下，即可确定完整齿廓曲线上每一点全局坐标。

2 齿轮动态啮合二次开发

齿轮动态啮合的二次开发是建立在MATLAB所具有的强大的函数编写功能、数值处理和文件处理能力之上，以文本文件为媒介，依据上述推导表达式在MATLAB中编写计算齿廓曲线上每一点坐标值的函数，根据齿轮参数计算齿廓曲线上每一点的坐标值并存入文本文件。同时，使用ABAQUS脚本接口语言Python直接读入已经存入文本文件的齿廓曲线上点的坐标，绕过ABAQUS/CAE的图形用户界面GUI［4］，直接对ABAQUS内核进行操作，进而实现齿轮从建模、定义材料属性、加载、网格划分、求解查看结果的处理。实际建模过程中，将齿廓曲线离散成若干节点，再由点生成线生成面生成体。利用MATLAB中system命令直接在MATLAB界面中驱动整个分析任务开始至结束，整个分析过程完全在MATLAB界面中完成，避免手动切换软件的繁琐过程［5］，详细的程序流程图如图2所示。其中接触建模前处理过程中，将主从动齿轮齿面集合定义为接触对，约束主从动齿轮除轴向转动外的所有自由度，同时主动齿轮施加恒定转速，从动齿轮施加负载转矩［6-8］。单元选取能够承受扭曲变形的线性减缩积分六面体单元C3D8R，对轮齿接触部分进行网格局部细化。后处理过程中，由于接触计算所有的结果数据都保存在输出数据库文件中，用户可根据自身需求提取其中的结果数据，并以文本文件的形式输出。

图2 程序流程图

3 修形齿轮动态啮合实例分析

通过所开发的程序对一对齿轮副进行不同转速下的齿轮啮合传动性能分析，齿轮副的具体参数如表1所示。

表1 啮合齿轮副基本参数

3.1 不同转速下啮合性能分析

齿轮传动经常使用于不同转速下的工作场合，因此通过转速建立对比模型，研究转速对齿轮动态啮合性能的影响。

为了避免强烈的初始啮合冲击，在前处理中给主动轮1.5ms的加速时间，只研究1.5ms以后的齿轮动态性能［9］。分别给主动轮施加转速70rad/s、80rad/s，从动齿轮施加恒定负载转矩120N·m。为了说明不同转速下齿廓节点应力变化情况，选取主动齿轮分度圆处两临近单元的质心处应力的平均值作为主动齿轮分度圆处应力，如图3所示。主动齿轮分度圆处点的应力情况如图4所示，可以看出随着转速增大，由于动载荷的增大的缘故，接触应力也随之增大。

图3 主动齿轮分度圆处单元

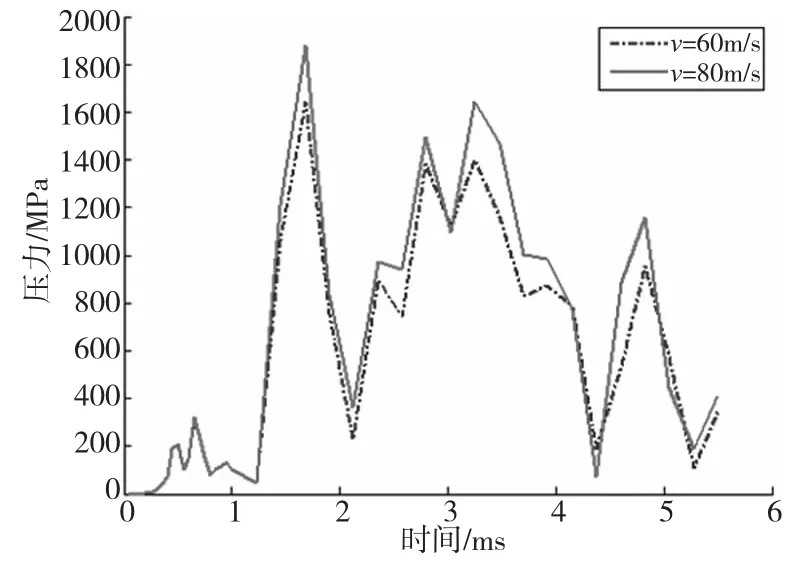
图4 主动齿轮分度圆处应力变化曲线

3.2 修形前后啮合性能分析

为研究修形对齿轮啮合性能的影响，对主动齿轮齿顶区域按表1参数进行齿顶修形。对主动轮施加恒定转速80rad/s，从动齿轮施加恒定负载转矩120 N·m。选取靠近齿顶的六个连续单元，并取这六个单元质心处应力的平均值作为齿顶区域的应力指标，齿顶区域应力变化情况如图5所示。由图5可以看出，标准齿轮在3.3ms以后开始逐渐退出啮合，在退出啮合过程中会出现强烈的啮出冲击现象。在齿轮退出啮合过程中，按表1所示的修形齿轮可以缓和啮出冲击，使齿轮在退出啮合过程中的应力变化相对平缓。

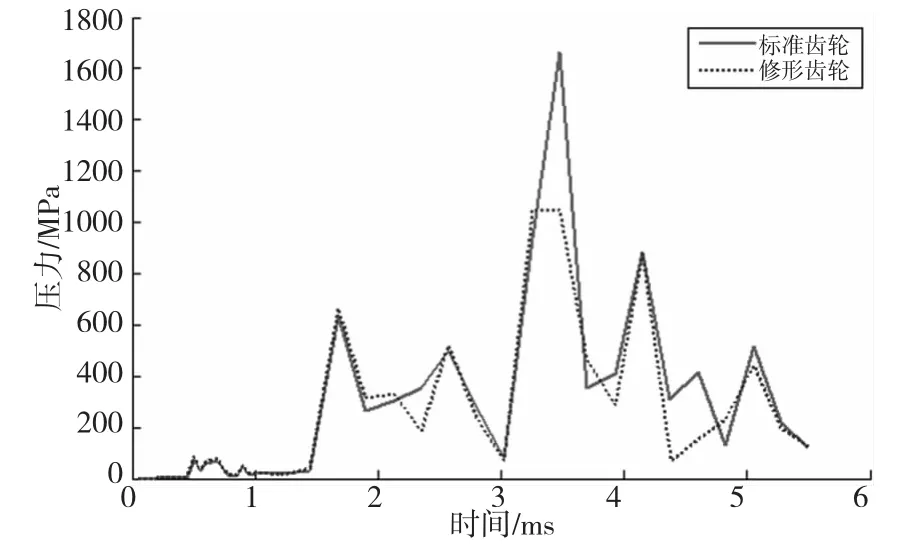
图5 主动齿轮齿顶区域应力变化曲线

4 结论

（1）联合商业软件MATLAB与Python脚本语言进行二次开发，实现了修形齿轮的参数化建模，以及动态分析的CAE流程自动化，可为齿轮的动态设计提供可行途径。

（2）对比分析相同转速下渐开线［参考文献］

直齿圆柱轮副与基于幂函数的修形齿轮副的动态接触性能，发现通过选取合适的修形参数可缓和轮齿在退出啮合过程中由于主动齿轮与从动齿轮基节不相等所造成的啮合冲击，提高齿轮的接触稳定性，分析结果对于研究齿轮传动提供了重要的参考价值。

［1］赵腾伦.ABAQUS6.6在机械工程中的应用［M］.北京：中国水利水电出版社，2007.

［2］王亮.渐开线圆柱齿轮齿廓修形设计及动态接触分析［D］.山西：太原理工大学，2012.

［3］田培棠.圆柱齿轮几何计算原理及实用算法［M］.北京：国防工业出版社，2012.

［4］曹金凤.Python语言在Abaqus中的应用［M］.北京：机械工业出版社，2007.

［5］杨艳.修形齿轮数字化设计方法与技术［D］.山西：太原理工大学，2012.

［6］Simulia.ABAQUS scripting referencemanual［z］.2008

［7］Giorgio Bonori，Marco Barbieri，Francesco Pellicano.Optimum profilemodifications of spur gears bymeans of gen-etic algorithms［J］.Journal of Sound and Vibration.2008，313（3 -5）：603-616.

［8］Conry T F，Seireg A.Amathematical programming techni-que for the evaluation of load distribution and optimalmodi-fication for gear systems［J］.A-SME Journal of Engineering for Industry.1973，35（2）：1115-1122.

［9］LIUYang.Parametric Modelingand Contact Analysis of Involute Spur Gears based on APDL［J］.Machinery-Design& Manufaeture，2014-（3）：65-78.

（编辑 赵蓉）

M odeling and Simulating of M odification Gear Based on Power Function

MA Yuan-jie1，ZHOU Jin-yu1，DING Qian-jin2，WANG Li-ming1，LIPu-yi1
（1.Hi-tech Key Laboratory of Equipment Remanufacture，Jiangsu University of Technology，Changzhou Jiangsu 213001，China；2.School of Software，TONGJIUniversity，Shanghai200092，China）

Recently，gear transmissionmechanism develops towards the tendency of high-speed，overloading and efficiency，this tendency puts forward high stability，high reliability，low noise on gears.Tomeet these design requirements，this article comes up w ith the method of tooth profile modification gears which are based on power function.Besides，it completes geometricalmodel building of the gears.In order to improve the efficiency and precision of the gear transm ission simulation，it brings in MATLAB and script language Python and conducts a secondary development in the environment of ABAQUS.As a result，it comes true parameterization process from modeling to the post-processing.At last，it analyses dynam ic meshing performance of gear transmission before and aftermodification under the same rotational speed.The accuracy and efficiency of this analytical process is verified by a practical example.Besides，it lays the foundation for dynam ic design of gear transm ission and provides a feasiblemethod.

gear tooth modification；parameterization；power function；Matlab；Abaqus

TH132.41；TG506

A

1001-2265（2015）08-0063-03 DOI：10.13462/j.cnki.mmtamt.2015.08.016

2014-11-03

国家自然科学基金项目（51275221）；江苏省产学研联合创新资金项目（BY2014038-04）；江苏省"333工程"培养资金资助项目

马元节（1988-），男，江苏淮安人，江苏理工学院硕士研究生，研究方向为齿轮传动系统，（E-mail）myj1040471049@163.com。