圆柱类工件圆柱度建模与公差分析*

袁世先，黄闻启

（1.河南职业技术学院机电工程系，郑州 450046；2.河南省矿业耐材有限公司，郑州 450053）

圆柱类工件圆柱度建模与公差分析*

袁世先1，黄闻启2

（1.河南职业技术学院机电工程系，郑州 450046；2.河南省矿业耐材有限公司，郑州 450053）

鉴于圆柱度误差会影响圆柱形零件的装配条件极其精密产品的性能，提出了一种用于圆柱类零件圆柱度建模及其误差分析的方法，首先利用L-F方程和群粒子优化算法分别对圆柱度误差进行建模和评估，然后利用Monte Carlo模拟法对轴和孔的虚拟装配发展而来的接触法以确定其位置精度。圆柱度误差和谐波次数（即谐波波瓣数）对零件位置精度的影响将会进行详细的分析，并通过对已有文献中的数据进行仿真试验和比较。结果表明在两个圆柱形工件间的圆柱度误差对位置精度的影响比圆度误差更为显著，并且证明上述建模和评估方法的有效性；当通过测量获得被加工零件的设计公差和几何误差后，该方法还能够快速地预测出相应的位置精度。

圆柱度误差；L-F方程；位置精度；公差分析

0 引言

在机械加工中，圆柱形零件的装配条件受制于诸如配件圆柱度误差等尺寸公差和几何误差，并对精密产品的性能有着显著的影响。目前，装配条件最主要的评估方式是利用通常被忽略的尺寸公差和几何误差，只有少数的研究人员致力于研究圆度误差对二维装配条件的影响［1-2］。为了确定两个圆柱体零件间实际配合状态，需要对零件的几何误差给予考虑。圆柱度误差实质上是由横截面的圆度误差引起的，而诸如轴向截面锥度、椭圆、棱圆和母线弯曲（凸形、凹形和鞍形）等形状误差则由圆柱正截面上直径的变化引起的［3］。对于圆形和圆柱形零件形状误差的建模过程，大多数研究人员专注于圆度误差的模型，并将该模型用作圆柱度误差模型的基础［4］。Mesay T.D.［5］等人提出一种能将圆形要素的总形状误差分解为系统和随机分量两部分的方法，傅里叶分量常用于表示由径向波动引起的系统形状误差，并且仿真和实验证明上述方法能描述很多种系统形状误差的特征。一些研究人员致力于如何建立圆柱度误差模型［6］和分析其对产品性能的影响。Zhang等［7］致力于机械加工圆柱形工件的典型几何误差及相应的误差源研究，并提出一种基于Legendre-Fourier（L-F）多项式的新方法以建立和描述典型几何误差的模型与特征。对于包括尺寸公差和几何误差在内的所有零件误差，均能够分解为一系列的L-F方程，每一个L-F方程通常表示一个制造系统中的误差源。因此在生产过程中，L-F方程可以消除已经确定的误差，从而使得加工过程可控。在本文中，使用L-F方程建立圆柱度误差模型以及采用粒子群优化（Particle Swarm Optimization，简称PSO）算法评价圆柱度误差，然后使用Monte Carlo模拟法对轴和孔进行虚拟装配以确定其位置精度。通过对结果的比较，表明圆柱度误差对圆柱形零件位置精度的影响比圆度误差更为显著。此外，圆柱度误差和谐波数对位置精度的影响也进行详细分析。

1 圆柱形部件的圆柱度建模

1.1 利用L-F多项式建立圆柱度误差模型

工件经过诸如车削和磨削的加工工序后，使用检测装置（如三坐标测量机，简称CMM）获取以加工工件的几何学数据组｛r，θ，z｝或｛x，y，z｝，这些几何的数据组可以数学分解为L-F多项式方程，如公式（1）所示：

其中，r是工件在（θ，z）点的半径，r0为工件的平均半径，Δr为工件在z截面处的形状误差，Pj（z）为Legendre方程，A和B是常数，并且正余弦函数是傅立叶级数的部分［8］。因此，公式（1）的每一个方程都是Legendre多项式和傅立叶级数的乘积，Pj（z）是完全正交于z坐标轴。同时傅立叶级数完全正交于截面坐标θ，傅立叶级数和Legendre多项式合理选择有如下两种方法：。由于圆柱形零件表面横截面方向的几何误差通常具有周期性，故用傅立叶级数描述其横截面方程。但是傅立叶级数并不适用于圆柱体截面，这是因为沿轴向的表面轮廓是不具有封闭性和周期性，反而其更适合用多项式表示。选取圆柱体的中心点作为轴坐标系的原点，在整个对称的区间使用恒定的权重函数。Legendre多项式在实际生产制造中相当于特有的制造误差［9］，故其适合于轴向表达式。

傅立叶级数的属性常用于建立圆度误差模型［10］，因此这里仅仅讨论Legendre多项式的属性。

前6阶Legendre多项式如下：

由于L-F多项式函数正交，故其系数可由公式（4）和（5）得到：

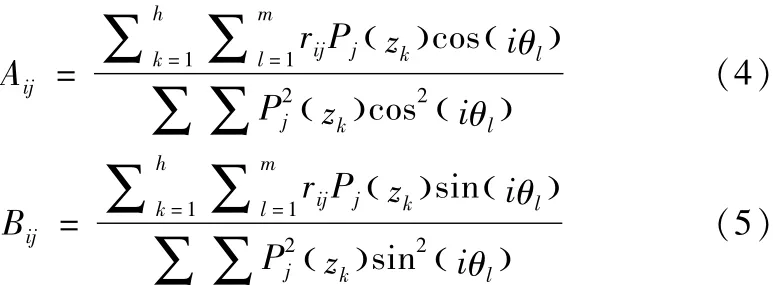
其中，l和m为方位角的顺序和总数，k和h分别为z方向上点的顺序和总数。

表1列举了圆柱形零件主要的制造误差和相应的L-F多项式表示［7］。注意不同的误差可能使用相同的多项式模型参数表示。例如，由刀具安装和工件膨胀引起直径误差属于相同类型的误差，故均可用A00表示。

表1 典型制造误差及相应的L-F多项式表示

1.2 圆柱度误差仿真

为了模拟轴和孔的圆柱形轮廓，因此假设圆柱体的轴线是理想的直线以及所有横截面的中心重合。文献［1-2］中采用相同的轴孔装配作为实例进行讨论，示例的名义直径254.00mm，且依据ASME B4.1确定尺寸公差，如图1所示。

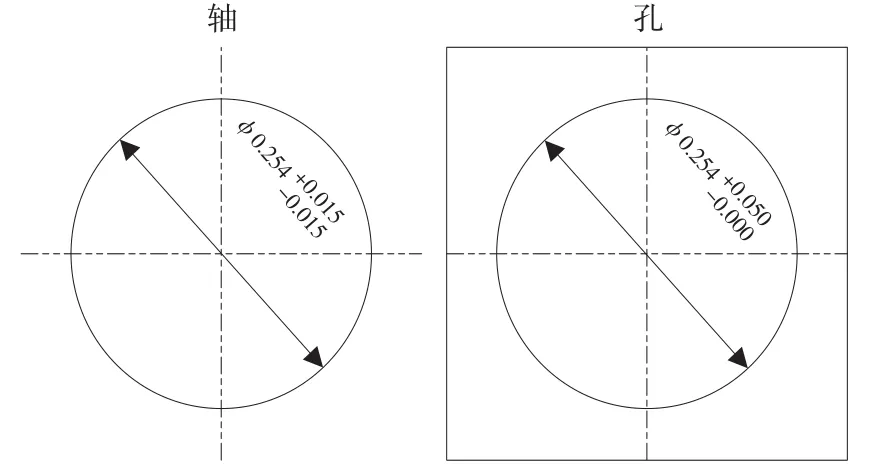
图1 两个含形状误差的配合零件实例

设定在横截面上的点数i为180且横截面的个数j也为180。图2表示包含圆柱度误差的轴和孔几种典型轮廓，它们可利用圆柱坐标系中的数据点｛r，θ，z｝构建获得，当然这些轮廓通过CMMs获取笛卡尔坐标系中的数据点｛x，y，z｝模拟得到。

从图2a～图2b中，轮廓在横截面上分别具有3次、4次和5次谐波圆度误差，一般情况下，从第2次到第50次谐波完全能够描述圆度误差，并且谐波次数（即波瓣数）越大，则与之对应圆柱度误差就越小；换而言之，当谐波次数接近于无穷大时，零件的圆柱度误差就无限接近于0。因此图2d为利用文献［1］中的谐波系数确定的截面轮廓。

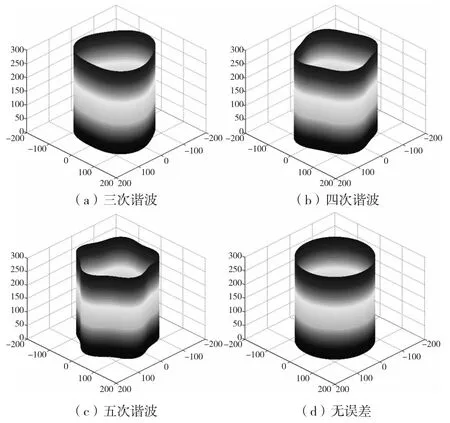
图2 圆柱形零件的径向谐波误差模拟

图3 圆柱形零件的轴向误差模拟

图3描述圆柱体在轴向的形状误差，如锥形、香蕉形、桶形和漏斗形等。其中图3a的轴向误差为一次LF多项式，其他均高阶L-F多项式。此外，图3b的中心轴线为曲线，其他的轴线（即母线）均为直线；从图中可以很明显地看出，轴线的直线度对零件的圆柱度有很大的影响，因此在实际加工中要尽量避免。

2 评估模拟圆柱形零件的圆柱度误差

在精密装配过程中，合理选取圆柱形零部件的参数是非常重要的，尺寸公差和形状误差对装配条件均有较大的影响，包括圆度误差和圆柱度误差等。将两个零件轴线间所允许的最大位移定义为零件的位置精度，并且一个零件的轴线被看作另一个零件的基准。圆柱度误差可通过两个同轴圆柱形轮廓之间的最小区域来评价的。文献［11］提出一种评价圆柱体尺寸的新方法，利用B-样条曲线代替直线去描述圆柱体的轴线，但是样本大小对结果有很大的影响。最小二乘圆柱、最大内接圆柱、最小外接圆柱或最小区域圆柱（MZC）是普遍采用的方法，其中，由于MZC能够得出最小圆柱度误差而被广泛应用，利用公式（6）确定理想圆柱体的轴线：

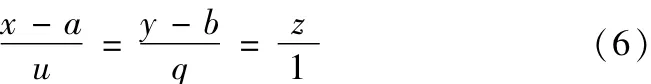
其中，a和b是位置参数，u和q是方向参数，表面上任意点到轴线的距离可通过下面的公式获得：

其中，i为方位角个数，j为截面个数，xij、yij、zij为轮廓上点的坐标。

利用MZC确定圆柱度误差是找到包含实际圆柱的两个同轴圆柱体，当这两个圆柱体的半径差最小时，圆柱体间的区域最小，且该半径差就是圆柱度误差。故评估圆柱度误差实际上是轴线的优化过程，目标函数为：

最近，用于圆柱度评估的最小区域可通过遗传算法［12］、粒子群优化算法［13］或解析几何法获得。由于PSO算法的高效性，因而在本文中用于评估圆柱度误差以及确定轴的位置和方向，图4为圆柱体轮廓仿真结果，从该图中可以看出，圆柱度误差为10μm。

图4 基于PSO算法的圆柱度误差评估

3 结果与讨论

3.1 相关文献中结果的比较

图5是在与文献相同条件下进行10000次迭代仿真后的结果。其中带三角形的折线表示文献［2］中的结果，图中两条曲线的对比显示不同位置误差具有相似的变化趋势，但其中考虑到圆柱度误差的位置误差要小于仅仅考虑圆度误差的情况。当没有形状误差时，其平均位置误差为25μm，而当圆柱度误差增加到30μm时，位置误差则下降到7μm，比仅仅考虑圆度误差时要小12μm。形状误差越大，这两种方法得到结果的偏差就越大，这表明轮廓误差实际上提高了轴和孔的位置精度。在文献［2］中，轴和孔被简化为带有形状误差的两个圆环，例如当只在二维平面内研究形状误差时。众所周知，圆柱体零件的实际轮廓是三维的，不同零件即使具有相同的形状误差，其横截面也可能是不同形状，因此文献［2］中的结果与实际情况有很大的出入。然而圆度误差仅仅能够处理不同横截面间的相互作用，圆柱度误差在径向和轴向都具有复杂得多的情况，并且尺寸公差可以抵消位置的变化。结果表明圆柱度误差对圆柱体零件间的位置精度的影响要大于圆度误差。

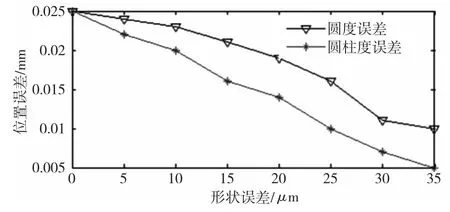
图5 形状误差与位置误差的关系

3.2 谐波次数和圆柱度误差对位置误差的影响

谐波次数影响工件圆柱度误差的主要因素，通过计算流体动力学仿真和试验，发现圆度波瓣和形状误差对柴油机零部件燃料泄漏有较大的影响。假设装配零部件间没有轴向误差，图6和图7表示当公称配合间隙相同时横截面的谐波次数和圆柱度误差对位置误差的影响。

图7 圆柱度误差对位置误差的影响

图6中的两个装配零件均有10μm的圆柱度误差，当横截面波瓣数增加时，位置误差减小。如果零部件有两个波瓣，则为椭圆形，当其长轴彼此相反时，其最大位置误差为24μm。这种情况下，轴在与孔接触之前其中心线沿长轴方向能够移动最长的距离，当长轴与短轴相反时，其中心线则能够移动最小位移。当轴的波瓣数增加到7时，其位置误差分别减小到14和12μm。孔的波瓣次数越高，则位置误差的值越小，这是因为波瓣间的相互作用阻碍了轴中心线的移动，即使当轴的波峰面对孔的波谷时。

图7表示圆柱度误差对位置误差的影响，孔的圆柱度误差为10μm，该图表明轴无论是三次或四次谐波，位置误差都随圆柱度误差的增加而减小。当轴的圆柱度误差为30μm时，位置误差为0，这意味着零部件间为过盈配合，原因在于零部件间的相互作用随着形状误差的增加而增加，且其相互作用可以防止轴中心线的偏移。显而易见，装配零部件的谐波次数越大，它们之间的位置误差就越小，如果其谐波次数无穷大，位置误差将依赖于形状误差所允许的最大轴半径和最小孔半径。

4 结束语

利用L-F方程建立圆柱度误差模型，采用PSO算法对其进行评估。通过对结果的仿真实验及比较，表明装配零部件的圆柱度误差对位置误差的影响要比圆度误差显著。圆柱度误差和谐波次数对位置误差将进行更为详细的分析，利用提出的方法，在测量获得尺寸误差或分配设计公差后，能够快速地预测零部件间的装配位置精度。

［1］Cho N，Tu J.Quantitative circularity tolerance analysis and design for 2D precision assemblies［J］.International Journal of Machine Tools and Manufacture 2002，42（13）：1391-1401.

［2］Cho N，Tu J.Roundnessmodeling ofmachined parts for tolerance analysis［J］.Precision engineering 2001，25（1）：35-47.

［3］黄祥.基于最小区域法的圆柱度几何误差评定［J］.组合机床与自动化加工技术，2013（6）：27-29.

［4］宁会峰，马广龙，龚俊.琦磨加工中圆柱度误差的评定方法研究［J］.机械设计与制造，2013（10）：224-226.

［5］Desta MT，Feng H-Y，OuYang D.Characterization of general systematic form errors for circular features［J］.International Journal ofMachine Toolsand Manufacture2003，43（11）：1069-1078.

［6］郑鹏，张琳娜，陈明仪.最小条件下零件圆柱度误差数学模型及其计量实现［J］.计量学报，2009，30（3）：197-200.

［7］Zhang X，Zhang C，Wang B，Feng S.Unified functional tolerancing approach for precision cylindrical components［J］.International journal of production research 2005；43（1）：25-47.

［8］周加喜，邓子辰，侯秀慧.夹层圆柱壳在移动内压作用下的临界速度研究［J］.应用数学和力学，2008，29（12）：1426-1434.

［9］陈一鸣，孙慧，刘乐春，等.Legendre多项式求解变系数的分数阶Fredholm积分微分方程［J］.山东大学学报（理学版），2013，48（6）：80-86.

［10］李英松，夏平，何东璠.基于傅立叶级数的立铣刀铣削力模型［J］.机械设计与制造，2012（7）：256-258.

［11］Zhang X，Zhang C，Wang B，Feng S.Unified functional tolerancing approach for precision cylindrical components［J］.International journal of production research 2005；43（1）：25-47.

［12］RamaswamiH，Anand S.Accurate size evaluation of cylindrical components［J］.The International Journal of Advanced Manufacturing Technology 2010；49（9-12）：1079-1092.

［13］张英堂，张光，李志宁，等.基于改进遗传算法的三轴磁场传感器校正方法研究［J］.现代制造工程，2013（4）：122-125.

［14］Changcai Cui，Shiwei Fu，Fugui Huang.Research on the uncertainties from different form error evaluation methods by CMM sampling［J］.International Journal of Advanced Manufacturing Technology，2009，43（1-2）：136-145.

（编辑 赵蓉）

Cylindricity M odeling and Tolerance Analysis for Cylindrical Components

YUAN Shi-xian1，HUANGWen-qi2
（1.Department of Electrical and Mechanical Engineering，Henan Polytechnic，Zhengzhou 450046，China；2. Henan Mining and Refractories Co.，LTD，Zhengzhou 450053，China）

The circular and cylindrical features are fundamental geometric features inmachines.Cylindricity error affects the fitting conditions of cylindrical components and impacts the performance of the precision products.In this paper，the cylindricity error was modeled using L-F functions and evaluated by particle swarm optim ization algorithm.Then the contact method is developed to determ ine the position accuracy through the virtual assembling of the bore and shaftusing themonte carlo simulation.The effects of the cylindricity error and the number of lobes on the position errorwere analyzed in detail.The results indicate that the cylindricity error hasmore significant influence on the position accuracy between the cylindrical parts than the roundness error.Using the suggested method in the paper，the position accuracy can be rapidly predicted after the design tolerances are allocated or the geometrical errors aremeasured onmanufactured parts.

cylindricity error；L-F functions；position accuracy；tolerance analysis

TH16；TG506

A

1001-2265（2015）08-0024-04 DOI：10.13462/j.cnki.mmtamt.2015.08.006

2014-11-03

河南省教育厅自然科学研究计划项目（2011c460007）

袁世先（1966-），女，贵阳人，河南职业技术学院副教授，研究方向为机械设计与制造，（E-mail）yuansx1966@126.com。