基于Hertz接触的滚珠丝杠副结合部刚度特性分析*

姬坤海，殷国富，王万金

（四川大学制造科学与工程学院，成都610065）

基于Hertz接触的滚珠丝杠副结合部刚度特性分析*

姬坤海，殷国富，王万金

（四川大学制造科学与工程学院，成都610065）

滚珠丝杠副传动时，螺母滚道和丝杠滚道与滚珠的接触方式是一种典型的非线性接触。基于弹性力学中Hertz接触理论，分析计算双螺母预紧滚珠丝杠副的轴向接触刚度。以某型号预紧双螺母滚珠丝杠副为例，建立其所受载荷与轴向接触变形的函数映射关系，推导其结合部接触刚度计算方法。针对其空载与承载两种不同状态，计算其结合部轴向接触刚度，并着重讨论了载荷对接触刚度的影响规律。基于有限单元法，对接触刚度计算结果进行数值验证，结果表明所建立的结合部接触理论模型能快速、准确的计算双螺母滚珠丝杠副的接触刚度，具有一定的理论价值和工程意义。

非线性接触；赫兹接触理论；有限单元法

0 引言

双螺母滚珠丝杠副采用预紧结构，减小了滚珠丝杠副的轴向接触间隙，从而使其轴向接触刚度和定位精度得到了提升，在高档数控机床进给系统［1-3］中得到了广泛应用。滚珠在丝杠滚道与螺母滚道之间的点接触滚动是一种典型非线性接触，这种接触的特性对滚珠丝杠副的动态稳定性和振动幅度有着重要的影响［4］。因此，研究滚珠丝杠副的接触特性以及借助Hertz接触理论建立轴向接触刚度理论模型，可为提高滚珠丝杠副的传动效率和工作性能提供理论依据。

近些年来很多学者运用赫兹接触理论对滚珠丝杠副的动力学特性进行了研究，如王丹等［5］从滚珠丝杠副的结构参数入手，基于Hertz接触理论分析了接触角、螺旋升角与接触变形、接触刚度之间的关系。Wei等［6］建立了滚珠丝杠副的动力学模型，分析了滚动体在运动时的传动效率和滑滚比。李凌丰等［7］通过现有的单螺母滚珠丝杠副弹性变形理论，建立了改进后的轴向变形公式。本文在已有的研究基础之上，基于Hertz接触理论分析预紧垫片的作用，进而来构造滚珠丝杠副的轴向接触变形理论模型和轴向接触刚度理论模型。建立双螺母滚珠丝杠副的有限元模型，对其进行非线性接触分析，然后观察轴向接触变形量随工作载荷的变化曲线的误差值来检验理论模型的正确性，也为分析计算其轴向接触刚度提供了一种普遍的计算方法。

1 力学特性分析

由于双螺母滚珠丝杠副具有垫片预紧结构，从而减小了螺母副的轴向接触间隙。图1力学模型图。垫片使螺母A和B、滚珠、丝杠紧密接触，且接触角方向恰好相反。

图1 力学模型图

螺母A、B与丝杠滚道面的法向压力分别为PA、PB，垫片的预紧力Fp，法向预紧力Pp。滚珠数目z，螺旋升角λ，接触角为β，则有：

无载荷时，即F=0时，PA=PB=PP。

承受工作载荷，即F≠0时，如图1所示，在工作载荷F作用下，工作螺母A的实际受力为FA，相对于预紧力的增量为F1；螺母B的实际受力为FB，相对于预紧力减少量为F2。于是有：

由双螺母滚珠丝杠的受力平衡条件可得：

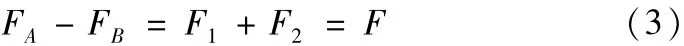
计算螺母中所包含的工作滚珠个数，计算公式是：

滚珠丝杠副的螺旋角λ［8］可以表为

式（4）、（5）中：i是螺母中滚珠的圈数乘以列数；db是滚珠直径；Ph是滚珠丝杠的导程；d0是丝杠副的公称直径。

2 轴向接触变形理论模型

在准确地构造其轴向接触变形理论模型过程中，需要以以下几点假设为前提：①假定轴向工作载荷均匀地分配给每一个滚珠上；②相互接触物体间只出现弹性变形，服从Hooke定律；③不计滚道表面与滚珠产生法向接触时导致接触角度的改变［9］，即假定接触角恒为45°；④忽略接触体之间的摩擦力；⑤接触面的尺寸要远大于接触物体表面的曲率半径。

考虑以上条件，可以认为滚道面与滚珠的弹性接触形变是由丝杠副的轴向变形量来决定的，从而应用赫兹弹性接触理论进行计算。

2.1 计算两弹性体间的相对位移量

如图2所示，通过法向力P作用，滚珠和丝杠滚道面的接触变形量［11］为δsp，滚珠和螺母滚道面接触点接触变形量为δnp，因为法向弹性接触变形丝杠滚道面与螺母滚道面间所产生的法向弹性位移量δn为：

图2 单个滚珠受力变形图

图3 接触压力空间位置图

由于丝杠滚道面与螺母滚道面之间在法线方向的相互作用，致使螺母相对于丝杠在其轴向产生轴向弹性变形量δa，如图3所示。

2.2 滚珠丝杠副轴向受力变形分析

2.2.1 无载荷受力变形分析

螺母A与螺母B中的滚珠受到法向力的作用而产生轴向接触变形，根据力的相互作用原理，两螺母受到的轴向预紧力大小相同、方向相反。因此双螺母滚珠丝杠副在无载荷作用下产生的轴向接触变形量为δp。

由式（17）可得：

2.2.2 承受载受力变形分析

在载荷F的作用下螺母A与螺母B产生的弹性接触变形量分别为δa、δb。δA、δB为在载荷F和预紧力FP作用下螺母A和螺母B产生的轴向接触变形量。在双螺母预紧滚珠丝杠副中，主要考虑由工作载荷引起的轴向接触变形量，也就是δa、δb。

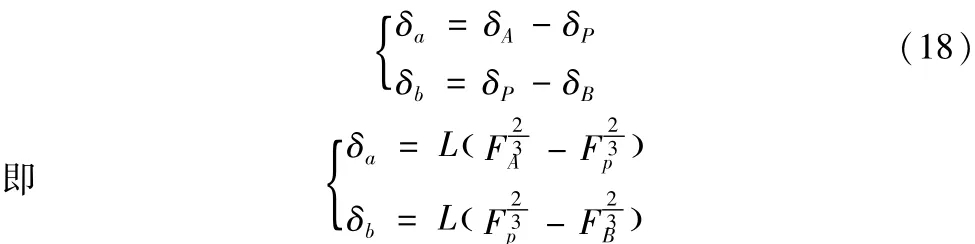
3 轴向接触刚度

按照变形相等原理，压缩变形量之和与弹性恢复变形量之和相等［12］。假设垫片为刚性体，在工作载荷与预紧力作用下不产生弹性形变。则有：

又有式（17）得，两弹性体的接触变形量与其法向压力2/3次方成正比［13］。联合式（19）可得：

已知轴向工作载荷F和预紧力Fp时，可由式（3）和式（20）联立求得FA、FB的值。

求得双螺母滚珠丝杠副中单个滚珠的轴向力后，由赫兹接触理论式（17）与式（18）求得工作螺母A以丝杠为参照所产生的轴向接触变形量，即轴向载荷F作用下的轴向变形量δ。

从而求得螺母组件的轴向接触刚度，即

由式（17）、（21）联立得：

4 轴向接触刚度计算结果分析

文中选取双螺母预紧滚珠丝杠副型号为THK公司BNFN5010-5，使用本文推导的滚珠丝杠副轴向接触变形和轴向接触刚度理论模型进行分析，其相关几何与物理参数如表1所示。

表1 BNFN5010-5滚珠丝杠设计参数

4.1 载荷与轴向接触变形的关系

依据已经构造的轴向接触变形理论模型式（17），如图4所示，可得到双螺母预紧滚珠丝杠副的轴向接触变形量随工作载荷变化的变化曲线。

图4 轴向接触变形量与轴向工作载荷的关系

分析图4可知，双螺母预紧滚珠丝杠副的轴向接触变形量随轴向工作载荷的增大而近似呈线性增大。由此也说明文中通过赫兹接触理论得到的双螺母滚珠丝杠副变形曲线接近线性的变化与文献［11］的结论吻合。

4.2 轴向接触刚度与载荷的关系

根据式（21）建立的轴向接触刚度K与载荷的关系如图5所示。

分析图5可知：轴向接触刚度K随工作载荷的增大而减小，在载荷较小时比较稳定。同时，双螺母滚珠丝杠副轴向接触刚度在工作载荷为500～8000N时，其总体变化相比单螺母滚珠丝杠副的轴向接触刚度要小，稳定性好［14］。这也是双螺母预紧滚珠丝杠副广泛应用于高速、高精密数控机床及各种自动化设备的主要原因之一。

图5 轴向接触刚度与轴向工作载荷的关系

5 有限元分析

使用有限元软件对双螺母预紧滚珠丝杠副轴向变形进行有限元分析。滚珠与螺母和丝杠之间的接触是一种高度非线性关系［15］。通过有限元分析方法，借助有限元分析软件来仿真非线性接触问题是目前常用的一种分析求解方法。把已经简化处理的有限元模型导入有限元分析软件，基于软件自身所带的有限元方法分析计算双螺母滚珠丝杠副在负载作用下的轴向接触变形。

5.1 简化有限元模型

BNFN5010-5型号双螺母预紧滚珠丝杠副的材料是轴承钢，查阅手册可知，密度ρ= 7.84mg/mm3，泊松比μ=0.3，弹性模量E= 2.01e11Pa，图6为经过简化处理的双螺母滚珠丝杠副有限元模型的二维［16］模型，这样的简化处理可以提高有限元分析软件的计算速度，使用PLANRE182为有限元单元。

图6 双螺母预紧滚珠丝杠副有限元模型

5.2 有限元分析前处理

非线性接触分析中需要合理的设置接触对，否则会影响到接触分析的结果。根据双螺母滚珠丝杠接触状态，分别在滚珠与螺母、丝杠之间建立二维面面接触单元。由图6可知，共有四处接触点需要建立四组接触对。

双螺母滚珠丝杠副在无载荷作用下只受到预紧力作用时，如图6所示，在有限元模型中对边1施加全约束即：工作螺母与预紧螺母在X、Y方向上约束；边4施加Y方向约束即：丝杠轴只能进行轴向（X方向）：对边2施加2890N预紧力即：预紧螺母施加的预紧力为2890N。然后双螺母滚珠丝杠副在无载荷作用下进行分析。在双螺母滚珠丝杠副受到工作载荷作用时，约束状态与无载荷作用时相同，需要在边3即：丝杠上加上向右的轴向力。然后对有限元模型进行加载，之后检查模型并设置相关参数进行求解。

5.3 结果分析

当双螺母滚珠丝杠副受到轴向工作载荷（1000N）与预紧力时，通过有限元分析软件得到的应力分布图，如图7所示。图中三角形形状为接触点的应力，且应力最大值在滚珠与滚道的接触点附近。图8为经过有限元分析得到的轴向位移图。

图7 滚珠丝杠副接触状态应力分布图

图8 双螺母滚珠丝杠副轴向变形云图

在对其进行有限元分析时，为了简化模型将双螺母滚珠丝杠副的螺旋角假设为零，即λ=0。若考虑到螺旋升角的因素，根据式（12）的关系式，需要将得到的有限元结果与螺旋升角的余弦值相乘。

表2为分别对双螺母滚珠丝杠副的轴向接触变形理论模型和轴向接触有限元模型施加500～8000N范围内的16个工作载荷，得到两种模型下的轴向变形量。

分析图9可知，两种分析方法的误差较小；进而说明了文中构造的轴向接触变形理论模型与轴向接触刚度理论模型的合理性。因此，双螺母滚珠丝杠副轴向接触变形理论模型为工程中快速计算双螺母滚珠丝杠副的轴向接触刚度提供了一种方法。

6 结束语

（1）运用弹性力学中的赫兹接触理论知识，依据双螺母滚珠丝杠副的结构特点，分析计算了其轴向接触变形理论模型，并进一步得出了其的轴向接触刚度理论模型。

（2）以BNFN5010-5型号双螺母预紧滚珠丝杠副为例，分析计算了滚珠与丝杠、螺母结合部的弹性变形量和接触刚度随工作载荷的变化规律。

（3）对其有限元模型进行仿真分［参考文献］

析，通过图9双螺母滚珠丝杠副轴向变形对比图可知两种分析方法的误差较小；进而说明了文中构造的双螺母滚珠丝杠副轴向接触刚度理论模型的合理性。研究的结果对于双螺母预紧滚珠丝杠副的设计和理论计算都有很好的参考价值。

［1］Wei C C，Lai R S.Kinematical analyses and transmission efficiency of a preloaded ball screw operating at high rotational speeds［J］.Mechanism and Machine Theory，2011，46（7）：880-898.

［2］Fukada S，Fang B，Shigeno A.Experimental analysis and simulation of nonlinear microscopic behavior of ball screw mechanism for ultra-precision positioning［J］.Precision Engineering，2011，35（4）：650-668.

［3］郑子文.超精密机床伺服控制技术研究［D］.长沙：国防科学技术大学，2001.

［4］Feng GH，Pan Y L.Investigation ofball screw preload variation based on dynamic modeling of a preload adjustable feed-drive system and spectrum analysis of ball-nuts sensed vibration signals［J］.International Journal of Machine Tool&Manufacture，2012，52（1）：85-96.

［5］王丹，王文竹，孙志礼，等.滚珠丝杠副接触变形影响因素分析［J］.东北大学学报（自然科学版），2011，32（4）：567-570.

［6］Wei Chinchung，Lin Jenfin，Horog Jenghaur.Analysis of a ball screw with a preload and lubrication［J］.Tribology International，2009，42：1816-1831.

［7］李凌丰，刘彩芬.滚珠丝杠副轴向变形分析［J］.中国机械工程，2011，22（7）：762-766.

［8］许向荣.滚珠丝杠副直线导轨进给单元动态性能研究［D］.济南：山东大学，2011.

［9］刘彩芬.滚珠丝杠副接触分析及定位精度测试系统设计［D］.杭州：浙江大学，2011.

［10］冈本纯三.球轴承的设计计算［M］.北京：机械工业出版社，2003.

［11］吴长宏.滚珠丝杠副轴向接触刚度的研究［D］.长春：吉林大学，2008.

［12］程光仁，施祖康，张超鹏.滚珠丝杠副设计基础［M］.北京：机械工业出版社，1987.

［13］蒋书运，祝书龙.带滚珠丝杠副的直线导轨结合部动态刚度特性［J］.机械工程学报，2010，46（1）：92-99.

［14］许向荣，宋现春，姜洪奎，等.单螺母滚珠丝杠副轴向刚度的分析研究［J］.武汉理工大学学报，2009，31（24）：54-57.

［15］王福吉，阳江源，贾振元，等.滚珠丝杠副非协调性接触特性研究［J］.中国机械工程，2011，22（19）：2293-2297.

［16］宋现春，姜洪奎，向荣，等.高速滚珠丝杠副弹性变形的有限元分析［J］.北京工业大学学报，2009，35（5）：582-585.

（编辑 赵蓉）

Study on Contact Stiffness Characteristics of Ball Screw by the Hertz Contact Theory

JIKun-hai，YIN Guo-fu，WANGWan-jin
（School of Manufacturing Science and Engineering，Sichuan University，Chengdu 610065，China）

The contactbetween ballsand nut races or screw races is a kind of typicalnon-linear contact.The axial stiffness of a double-nut ball screw was analysed and calculated by using the Hertz Contact Theory of elasticmechanics.A double-nut ball screw is selected as an example，the function of the axial contact deformation and the cutting load was built，and the contact stiffnessmodelwas developed.Under the situation w ith and w ithout the cutting load，the axial stiffness of joint partwas investigated，and the effect of cutting load was focused on.Finally，the finite elementmodelwas employed to verified the theoreticalmodel.The analytical results show that it can not only calculate the contact stiffness quickly and exactly，but also offer theoretical support and engineering meaning.

non-linear contact；Hertz contact theory；finite elementmethod

TH132.1；TG506

A

1001-2265（2015）08-0001-04 DOI：10.13462/j.cnki.mmtamt.2015.08.001

2014-07-22；

2014-12-19

国家科技重大专项课题“高档数控机床与基础制造装备”（2013ZX04005-012）；四川省科技支撑计划课题（2011CGZ0050）

姬坤海（1988-），男，河南温县人，四川大学硕士研究生，研究方向为机床典型结合面动力学，（E-mail）jikunhai@126.com。