略谈三种数学思想在小学数学教学中的应用

◎福建省连城县宣和中心小学　项如榕

略谈三种数学思想在小学数学教学中的应用

◎福建省连城县宣和中心小学项如榕

数学是一门培养和锻炼学生数理逻辑能力的基础性科学，也是一门应用性极强的工具性学科。数学思想方法是对数学本质特征的认识。在小学数学教学过程中渗透思想方法教育，有助于提高学生正确认识和理解数学，培养数理思维的能力。本文从数形结合思想、化归思想、等量变换思想三方面论述数学思想方法在教学中的运用，以探讨培养学生数理逻辑能力。

数学思想；典型；应用

数学思想方法是数学知识的精髓，又是知识转化为能力的桥梁。小学数学中蕴含着丰富的数学思想方法，需要我们去挖掘并实施于解决问题的过程中。

一般来讲，小学数学所涉及的思想方法主要有数形结合、分类、结合、化归、归纳、建模、等量变换、类比、假设、可逆等等。数学思想方法并不单纯是解决一类数学问题的捷径，实际上反映了数学整体内在的规律和逻辑。在小学数学教学过程中渗透思想方法教育，不仅是提升数学学习兴趣，打造兴趣课堂的必由之路，也是引导学生正确认识和理解数学，培养数理思维，实现素质教育目的的题中之义。本文拟选取三种典型性数学思想方法予以介绍，并附实例说明数学思想方法在教学实践中的应用。

一、应用数形结合思想，化抽象为直观

数形结合思想是数学的重要思想方法之一，在数学教学实践中应用极为广泛，也是数学研究常用的方法。数形结合，顾名思义，即将数量关系与图形相结合，通过线段、几何面积、集合等图示把数字所表示的数量关系通过图形直观地表达出来，从而使原本抽象的数学问题化为具体形象，进而提升学生的学习兴趣，提高教学效果。

例如，在处理容斥关系一类的问题上。假设某班有学生若干，班里的学生必须至少参加一项体育运动，其中有35人参加篮球运动，21人参加乒乓球运动，有9人两项运动都参加了，求班上共有多少名同学。对于很多小学生来讲，读完题目就已经晕头了，不知如何着手，但如果根据题设条件做出韦恩图（如图1），则问题的答案就相当显明了。从图上可以很直观地看到9人是重复的部分，应该用参加两种体育运动的总数减掉重复的部分就是全班的总人数，即35+21-9=47（人）。

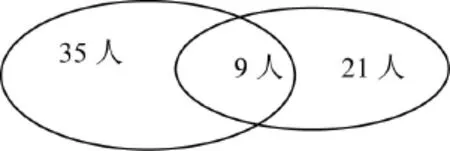
图1

再比如，处理鸡兔同笼问题时，也经常用到数形结合思想。假设笼子里鸡和兔子共8只，腿有24条，请问笼中有鸡和兔子各几只。用方程来解答，设有鸡x，则兔子个数为8-x，从而得到2x+4×（8-x）=24，从而得出有鸡与兔子各有4只。这种方法作答，固然为最佳的计算方法，但对于小学生来讲，往往较难理解，而借助数形结合的思想，则不仅有助于将题目作对，还能加深对一元一次方程的理解。如图2，先画8个圆代表鸡兔总数，假设全是鸡，则在各圆下画2条腿，结果还剩8条腿，从而在4个圆下各画2条腿，于是，从画好的图形中可知，有鸡4只，兔子4只。

图2

教学中经常遇到抽象难解的问题，题中繁杂的数量关系往往使学生一筹莫展。如果运用数形结合思想把数量关系与图形相结合，把数字所表示的数量关系通过图形直观地表达出来，将原本繁杂的数量关系问题予以简化，使问题变得直观易解。可见，通过作图的方式，将繁杂的数量关系简单化，符合小学生的认知水平和思维习惯。

二、应用化归思想，化繁杂为简约

“化归”即转化和归结之意，也是小学数学经常用到的思想。在解决数量关系复杂、计算量庞大的数学问题时，为了能简单快速地得出正确答案，往往会将一个复杂数量关系甲通过转化，归结为一个相对较为简单的数量关系乙来解决，通过解决乙问题而自然得到甲的答案。教师如果能在教学过程中引导学生灵活运用“化归思想”问题，可以有效地提高教学效率。

在四则运算中灵活运用化归思想，可以有效地减少计算量，提高解题的准确度。如在计算1.25×96×25时，如果按照一般的运算顺序来解答，往往计算较为复杂，而且也容易算错。如果运用化归思想，将计算式予以转化则问题会变得比较简单。如上式，96可以转化分解为8×4×3，这样1.25×96×25=1.25×8×4×3×25=（1.25×8）×（25×4）×3，1.25×8=10，25×4=100，因此，（1.25×8）×（25× 4）×3=3000。再如，48×53+47×48，可以转化为（53+47）× 48=4800，这其实也是化归思想的体现。

在解答应用题过程中，也常会应用到化归思想，从而使原本复杂的数量关系变得简单。如，某甲与某乙进行跳跃比赛，甲每次可以向前跳跃1.5米，乙每次可以向前跳跃1.8米，甲与乙每秒钟只允许跳一次。从比赛终点到比赛起点，每个5米设有一个休息区，问当甲乙二人任何一个恰好跳到休息区时，另外一个跳了多少米。乍看题目，往往一头雾水，但仔细分析一下题目，如果巧妙运用化归思想来解，问题就变得简单多了。通过题设可以知道，当有其中一人恰好跳进休息区时，此时他跳跃的路程应为1.5（或1.8）的倍数，同时又应该是5的倍数，亦即1.5与5或者1.8与5的最小公倍数，于是这样一个相对较为复杂难解的问题，通过化归，转化为一个单纯求最小公倍数问题。

从上述例子中可发现，化归思想就是要把复杂的数学问题，转化、归结为一个个基础性的问题来解决，使题目更加简化，计算更加快速、有效率。教学中灵活运用“化归思想”解决教学中遇到的难题，可以达到事半功倍的效果。

三、应用等量变换思想，化疑难为简易

所谓等量变换，即将一种等量转换到另一种等量，由一种形式转变为另一种形式的思想。它是代数思想方法的基础。等量变换不同于化归思想，虽然化归思想中有等量变换的体现，尤其在转化的环节，但化归实际上是转化和归结两个过程，而等量变换则仅仅涉及相同量的互换。

例如，求1/2+1/6+1/12+1/20+……+1/380的和，其中分数的分子均为1，但分母却各不相同，但仔细观察分母可以发现，2×1=2，，3×2=6，4×3=12，5×4=20……20×19= 380，由此可以发现规律，上述分子的一般项为1/n×（n+ 1），每个分数经过等量转换可得：（1/n-1）×（1/n+1）。因此，前面分子式，原式=1/（1×2）+1/（2×3）+1/（3×4）+1/（4× 5）+……+1/（19×20）=（1-1/2）+（1/2-1/3）+（1/3-1/4）+（1/ 4-1/5）+……+（1/19-1/20）=1-1/20=19/20。

事实上，在数学教育实践中，很多思想的应用并非孤立的，有时候一道题目的解答需要用到多种数学方法，而且，运用多种思想方法也可以解答同一道题。比如，在一场“形象小姐”大赛中，甲的专业得分为8.55分，综合得分0.88分，总分9.43分；已知乙的专业得分8.65分，综合得分0.4分，请问谁的比分高，高多少。按照一般的算法，9.43-（8.65+0.40）=0.38，可见甲的比分较高，高出乙0.38分。除此以外，还可以8.65-8.55=0.10，0.88-0.40=0.48，0.48-0.10=0.38，这里应用了对应的思想方法；8.65-8.55=0.10，就从0.88-0.10=0.78，再0.78-0.40= 0.38，应用了等量变换的思想。

数学思想方法是在数学教学和研究中所归纳形成的，体现了数学的本质特性和内在趣旨，在小学数学教学过程中应注意有目的、有选择、适时地进行渗透。运用数学方法解决问题的过程就是感性认识不断累积的过程，当这种量的累积达到一定度时就产生质的飞跃，从而上升为数学思想。因此，学生若能通过不断的解题实践，熟知数形结合，化归转换，等量变化等数学思想的运用就能潜移默化地习得数学的求解方法，更重要的是还能兼而习得数学的思维品质和习惯，习得对数学本质特征和规律的认知。

（责任编辑：陈志华）