具有尾翼的复杂导弹模型超宽带散射特性分析

2015-10-31周新鹏魏国华吴嗣亮王达伟

电子与信息学报 2015年8期

周新鹏魏国华吴嗣亮王旭王达伟

周新鹏*魏国华吴嗣亮王旭王达伟

(北京理工大学电子与信息学院北京 100081)

为了满足对复杂导弹测量和检测的需要，该文建立了具有尾翼的复杂导弹模型，研究在极窄脉冲照射条件下该导弹目标散射特性。利用时域有限差分(Finite-Difference Time Domain, FDTD)法计算该导弹模型的瞬时散射回波，分析远场电磁波不同入射条件下导弹散射回波特性及近场不同转角条件下导弹瞬时散射回波特性。通过对该导弹瞬时散射回波特性分析，得出了目标散射中心的成因及散射波形特点，在雷达应用领域具有一定的理论参考价值。

电磁散射；冲激脉冲；有限时域差分法；导弹模型；尾翼

1 引言

近年来，超宽带技术由于具有高距离分辨率，被广泛应用到雷达领域，例如，测距[1]、定位[2]、目标识别、成像[6,7]等。这些功能是雷达依据目标电磁散射回波来实现的，因此，研究目标瞬时电磁散射回波特性在雷达应用中具有重要意义。

早期超宽带电磁散射特性主要是在频域中完成的[8]。近年来，随着时域电磁学的发展，在时域研究目标散射特性引起了广泛兴趣。当极窄脉冲照射到复杂目标，其回波不再是简单的延时入射波的叠加，而是由目标材料、几何结构和视线角决定散射特性的散射中心回波的叠加。考虑到高斯脉冲特性、目标材料损失和电磁波与目标表面的相互作用，文献[9,10]引入目标冲激响应扩展因子，代替有限理想散射点简单叠加。平板、球体、圆柱体等简单目标的超宽带散射特性被广泛地研究，获得了大量实验数据。对于简单目标，在时域中，理论计算、真实实验、仿真试验数据结果都是一致的；但利用理论计算分析飞机、导弹这类复杂目标的散射特性难度较大，目前主要依赖于真实实验和仿真试验研究该类复杂目标的散射特性[17,18]。

本文以某型空空导弹为原型，以真实目标尺寸建立导弹模型，以一阶高斯微分为发射信号，利用时域有限差分(Finite-Difference Time Domain, FDTD)法研究该型导弹超宽带瞬时电磁散射特性。首先，建立真实尺寸的导弹模型；其次，在远场平面波、不同入射角条件下进行时域FDTD仿真，分析该导弹模型远场时域散射波形及散射特性；再次，在近场环境，基于单基地雷达，不同转角情况下进行时域FDTD仿真，分析该导弹模型近场瞬时散射特性。

2 数学模型

2.1 导弹模型

本文建立导弹3维模型如图1所示，该导弹模型有一个球冠、一个圆锥体、一个圆柱体及8个棱锥体组成，各部分尺寸如图1所示。在仿真中，导弹外壳材料选择为铜，导弹外壳厚度为1 cm，弹体直径为0.3 m，弹头球冠直径为0.05 m，弹头球冠与圆锥体相切形成光滑曲面，操纵舵前缘棱边与圆柱体的夹角为，尾翼前缘棱边与圆柱体的夹角为。

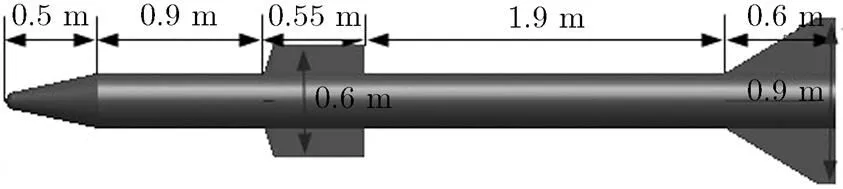
图1 导弹模型结构及其尺寸

2.2激励信号模型

3 远场导弹模型散射特性

3.1 远场仿真模型

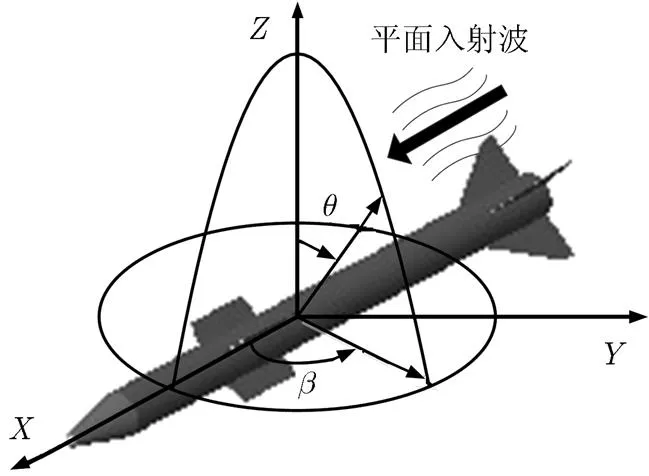
图2 远场导弹仿真模型

对于导弹而言，电磁波主要是对导弹前半球进行照射，因此仿真入射波仰角为，方位角分别为时的散射回波。图3为平面波激励信号和时的导弹目标散射回波。图3清楚地表明，入射方位角为时，本文提供的导弹模型有6个强散射回波，表1给出了各强散射回波到第1个强散射回波的测量距离。由表1可知，第1个强散射回波是由弹头球冠镜面反射形成的局部滑动散射中心，称之为弹头散射中心；第2个强散射回波是由锥体与圆柱体相交不连续处散射形成的边缘散射中心；第3个和第4个强散射回波分别是由操纵舵前缘和尾翼前缘与圆柱体连接处散射形成的；第4个和第6个强散射回波分别是由操纵舵后缘尖端和尾翼尖端电磁波绕射形成的。

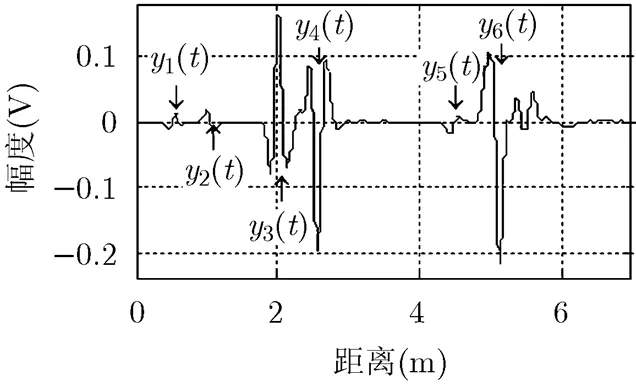
图3 入射角时的导弹散射回波

表1时导弹强散射回波的距离(m)

强散射回波i123456 00.5051.4682.0283.9434.576

为了研究导弹各强散射瞬时回波波形特点，计算波形保真度因子[13]。对于两个信号和，其波形保真度因子定义为

甲洛洛回到家里，想着自己家里，老婆带着三个儿子，也是饱一顿饿一顿，但还好，自己每个月有个十三块钱的工资。平时在食堂里节约好午饭，早饭和晚饭也就基本够吃了，可近来由于小阿布，自己也得捏紧裤袋。

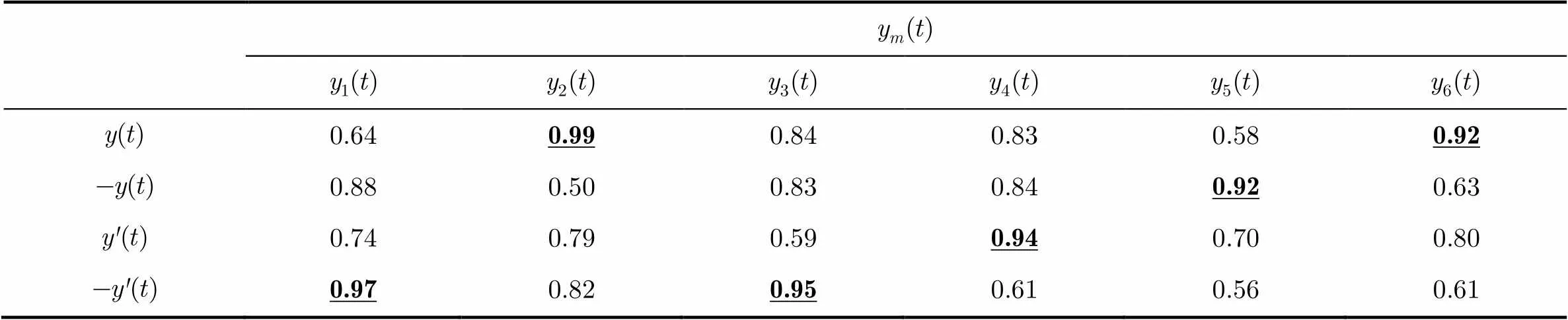
表2时导弹各强散射回波的波形保真度因子

0.640.990.840.830.580.92 0.880.500.830.840.920.63 0.740.790.590.940.700.80 0.970.820.950.610.560.61

表3时导弹各散射中心的距离(m)

散射中心i2345678 15º0.4591.4011.9383.8014.443-- 30º0.3991.2511.6293.3943.7813.9434.166 45º0.2800.9821.3201.5431.9562.9553.227

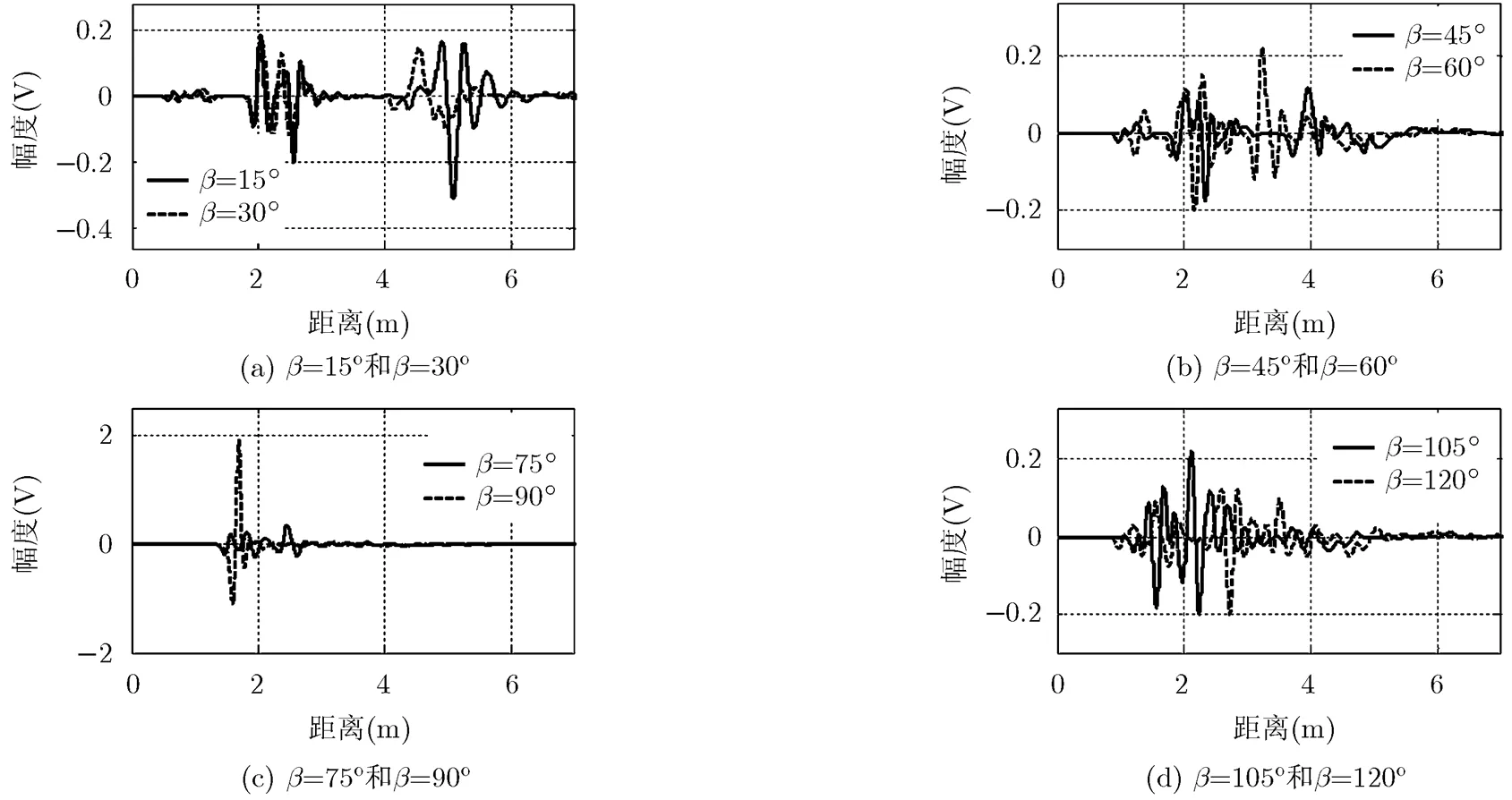
图4 在入射波仰角，不同方位角时的远场导弹目标散射信号

3.3不同仰角时的导弹目标散射特性

图5 不同入射波仰角时的导弹模型散射回波

由图4和图5可以看出，本文给出带有尾翼的导弹模型，其散射特性较为复杂，其复杂性主要表现在操纵舵和尾翼的散射特性。通过分析图4和图5，可以得到以下结论：

(2)弹头球冠散射中心散射波形为反相入射波微分，圆锥体与圆柱体连接处散射波形为入射波，操纵舵前缘和圆柱体连接处散射波形为反相入射波微分，操纵舵后缘绕射波形为入射波微分，尾翼前缘和圆柱体连接处散射波形为反相入射波，尾翼尖端绕射波形为入射波；

(3)电磁波在照射阴影区的舵和尾翼尖端产生绕射，形成散射中心；

(5)该导弹的电磁复杂性主要体现在操纵舵和尾翼的几何结构和尺寸上。

4 近场导弹模型散射特性

建立近场仿真模型如图6所示。天线到导弹中心=5 m，导弹围绕导弹中心在平面上逆时针转动，每次转动。选择的波形同上，极化方向为轴方向。由于是分析导弹散射特性，不考虑天线传递函数的影响，仿真中利用式(1)激励点源产生球面波，仿真场景边界为PML边界。图7为导弹在不同转角下的散射回波。

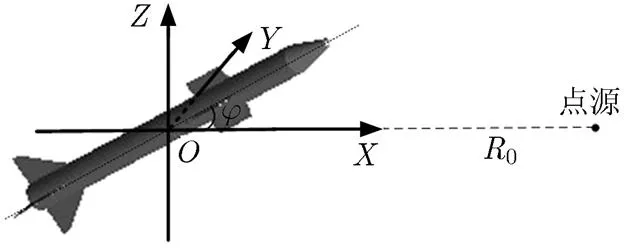
图6 近场导弹散射仿真模型

图7 近场导弹在不同转角的散射回波

表4导弹转角为时各散射中心回波的波形保真因子

0.380.530.510.680.760.69 0.470.500.670.510.550.44 0.680.600.860.780.910.83 0.670.790.780.860.750.83 0.890.820.980.800.790.73 0.700.890.790.980.970.99

同理可以得到产生垂直反射波的最大转角为

由式(7)和式(8)可知，产生镜面垂直反射波的范围和旋转点到点源的距离以及圆柱体的长度有关。在本文仿真中，转角范围在时，产生镜面垂直反射回波。

通过分析近场环境下基于单基地雷达的导弹散射特性，总结起来，可以得到如下结论：

(1)导弹在近场的散射中心位置和远场基本一致，但其散射波形有明显区别。

(2)近场导弹各散射中心的散射波形随着导弹目标转角变化而有所变化。

(3)导弹在一定转角范围内，其圆柱体表面会产生镜面垂直反射波，该散射中心的散射回波幅度远强于其它散射中心。

(4)在照射阴影区，电磁波在操纵舵和尾翼的尖端、棱角以及不连续处产生绕射，形成强散射中心。

5 结论

本文研究了带有尾翼复杂导弹的超宽带散射特性，首先通过分析远场该导弹的瞬时散射波的特点，研究了该导弹远场散射中心成因和随入射角变化特点，其次通过分析近场该导弹瞬时散射波特点，研究了近场该导弹散射中心随导弹转角的变化特点及产生垂直反射波的范围。通过对该导弹瞬时散射波特点分析，得到了该导弹超宽带散射特性的结论，这些结论对于该型导弹测量、成像、识别具有重要的理论参考价值。

参考文献

[1] Guvenc I, Sahinoglu Z, Orlik P,.. Searchback algorithms for TOA estimation in non-coherent low-rate IR-UWB systems[J]., 2009, 48(4): 585-603.

[2] Rongguo Z and Hao Xin. A novel direction of arrival estimation technique using a single UWB antenna[C]. Proceedings of 2010 IEEE Antennas and Propagation Society International Symposium,Toronto, Canada, 2010: 1-4.

[3] Salman R and Willms I. A novel UWB radar super-resolution object recognition approach for complex edged objects[C]. Proceedings of2010 IEEE International Conference on Ultra- Wideband, Nanjing, China, 2010, 2: 1-4.

[4] Ping F and Zhanrong J. Scattering center estimation of UWB radar target with improved MP method[C]. Proceedings of8th International Symposium on Antennas, Propagation and EM Theory, Kunming, China, 2008: 1075-1078.

[5] Paladini R, Ferro Famil L, Pottier E,.. Point target classification via fast lossless and sufficient invariant decomposition of high-resolution and fully polarimetric SAR/ ISAR data[J]., 2013, 101(3): 798-830.

[6] Salman R, Willms I, Sakamoto T,.. 3D imaging of a manmade target with weak scattering centres by means of UWB-radar[C]. Proceedings of2013 IEEE International Conference on Ultra-Wideband, Sydney, Australia, 2013: 109-112.

[7] Abe Y, Kidera S, and Kirimoto T. Accurate and omnidirectional UWB radar imaging algorithm with RPM method extended to curvilinear scanning model[J].

, 2012, 9(1): 144-148.

[8] Miller E K and Landt J A. Direct time-domain techniques for transient radiation and scattering from wires[J]., 1980, 68(11): 1396-1423.

[9] Hussain M G M. Principles of high-resolution radar based on nonsinusoidal waves. III. radar-target reflectivity model[J]., 1990, 32(2): 144-152.

[10] Hussain M G M and Safar Y A. Pole patterns of radar-target scattering model based on ultra-wideband gaussian pulses[C]. Proceedings of2001 CIE International Conference on Radar Proceedings, Beijing, China, 2001: 483-487.

[11] Imbs Y, Chevalier Y, Beillard B,.. UWB measurements of canonical targets with a new broad band wire antenna[C]. Proceedings of 1998 IEEE International Geoscience and Remote Sensing Symposium, Seattle, USA, 1998: 770-772.

[12] Tesche F M, Giri D V, and Prather W D. Scattered EM field responses of canonical scatterers illuminated by an impulse-radiating antenna (IRA)[J]., 2009, 51(3): 53-69.

[13] Lin L, Tan A E C, Jhamb K,.. Characteristics of ultra-wideband pulse scattered from metal planar objects[J]., 2013, 61(6): 3197-3206.

[14] Pancera E, Zwick T, and Wiesbeck W. Correlation properties of UWB radar target impulse responses[C]. Proceedings of 2009 IEEE Radar Conference, Pasadena, USA,2009: 1-4.

[15] Blalock S, Davis J, Denison D,.. Measured and FDTD calculated ultra wide band (UWB) RCS for treated test fixtures[C]. Proceedings of 2008 European Radar Conference, Amsterdam, Holland, 2008: 436-439.

[16] Zichang L, Wei G, and Jinpeng F. Narrow pulse transient scattering measurements and elimination of multi-path interference[C]. Proceedings of the International Symposium on Antennas & Propagation, Nanjing, China, 2013(1): 408-411.

[17] Sun H, Zhang Y, and Tian B. Study on ultra-wideband scattering characteristics of targets based on UPML- FDTD[C]. Proceedings of 4th Asia-Pacific Conference on Environmental Electromagnetics, Dalian, China, 2006: 640-643.

[18] 屈泉酉, 郭琨毅, 穆海舰, 等. 基于体目标相对稳定散射中心的脱靶量估计方法[J]. 系统工程与电子技术, 2013, 35(4): 692-699.

Qu Quan-you, Guo Kun-yi, Mu Hai-jian,.. Miss distance measurement based on stable scattering centers of extended targets[J]., 2013, 35(4): 692-699.

Analysis on Ultra-wideband Scattering Characteristics of Complex Missile with Empennages

Zhou Xin-peng Wei Guo-hua Wu Si-liang Wang Xu Wang Da-wei

(,,100081,)

In order to meet the requirement for measurement and detection of complex missile targets, a complex missile model with empennages is established and its scattering characteristics are studied under the conditions of the missile irradiated by extremely short pulse. Transient scattering echoes of the missile model are calculated using Finite-Difference Time Domain (FDTD) algorithm. The characteristics of the missile scattering echoes are analyzed at different incident angle conditions in far field and at different rotational angle of the missile in near field. These analyses on the scattering echo characteristics reveal the causes of the missile scattering centers and characteristics of scattering waveforms, which can provide theoretical reference in radar application.

Electromagnetic scattering; Impulse pulse; Finite-Difference Time Domain (FDTD) algorithm; Missile model; Empennage

TN011

1009-5896(2015)08-1868-06

10.11999/JEIT141238

周新鹏 xinpeng_780304@163.com

2014-09-23收到，2015-05-08改回，2015-06-09网络优先出版

周新鹏：男，1978年生，博士生，研究方向为超宽带雷达成像和信号处理.

魏国华：男，1977年生，副研究员，研究方向为雷达系统及其信号处理.

吴嗣亮：男，1964 年生，教授，博士生导师，研究方向为信号处理理论与技术、目标探测与识别理论与技术、电子系统仿真与信号模拟.