一种共享份分块构造的异或区域递增式视觉密码方案

郁 滨 胡 浩 陈武平 沈 刚



一种共享份分块构造的异或区域递增式视觉密码方案

郁 滨①胡 浩*①陈武平②沈 刚①

①(信息工程大学 郑州 450001)②(信息保障技术重点实验室 北京 100072)

该文依据授权子集的个数将共享份划分若干块，按照共享份分块构造的设计思路，结合(,)异或单秘密视觉密码的加密矩阵，构造了异或区域递增式视觉密码的秘密分享与恢复流程。与现有方案相比，该方案可以实现解密区域图像的完全恢复，且明显减小了共享份的大小。

视觉密码；区域递增；密级；分块构造；异或运算；完全恢复

1 引言

多秘密视觉密码方案(Multi-secret Visual Cryptography Scheme, MVCS)主要用来分享多幅独立的秘密图像，与MVCS不同，区域递增式视觉密码方案(Region Incrementing Visual Cryptography Scheme, RIVCS)将一幅秘密图像划分为多个区域，不同区域具有不同的图像，区域恢复数量与参与者人数有关，参与者人数越多，恢复区域的数目越多，只有当参与者全部到齐时才能恢复所有区域。在实际应用中，可以依据图像内容信息的敏感程度，将图像划分多个密级区域，对于高密级区域，需要更多参与者共同完成秘密恢复。因此，利用RIVCS区域递增式的解密特性能够有效保护秘密图像中的不同敏感信息，可以广泛地应用于信息的分级管理、多级访问控制和身份认证等方面，有效拓展了视觉密码的应用领域[10]。

文献[5]于2009年首次提出一种存取结构为(2,)的区域递增式视觉密码方案(OR-based RIVCS, ORIVCS)，将一幅秘密图像划分–1个区域，利用相应的加密矩阵对各区域分别分享，共享份以透明胶片作为载体，叠加(相当于或运算)任意()个共享份可以恢复-1个区域的秘密信息，但仅限于3, 4和5。文献[6]建立关于加密矩阵的线性规划模型，设计了像素扩展度最优的(2,)方案，将扩展到任意正整数，但原黑白像素在恢复图像中的颜色会产生反转。文献[7-9]通过拼接(,)单秘密或运算视觉密码方案[11](OR-based Visual Cryptography Scheme, OVCS)的加密矩阵设计了一种(,)-ORIVCS，突破了(2,)结构的限制，同时解决了黑白像素颜色反转失真问题，但随着和的扩大，像素扩展度迅速增大，对比度也随之降低，导致共享份的存储和传输开销急剧增加，且秘密图像的恢复效果逐渐模糊。

尽管以上RIVCS在存取结构方面不断拓展，但像素扩展度大、恢复效果不佳的问题没有得到有效解决[12]，事实上，现有方案主要依靠构造精简的加密矩阵来降低像素扩展度，对于原始图像中各区域的分享本质上仍是单秘密OVCS，在秘密恢复时，利用达到恢复门限值的区域被解密，未达到恢复门限值的区域无法解密实现区域递增式显示的效果。因而RIVCS的加密矩阵是OVCS加密矩阵的组合，导致加密矩阵的规模始终较大。文献[11]提出的最优的(,)-OVCS，像素扩展度为，对比度为。显然随着参与者人数的增加，即使是最优方案的参数也急剧变差，因而OVCS的恢复不佳直接制约了RIVCS恢复效果的提高。

为了改善单秘密方案的恢复效果，文献[13]将异或运算引入视觉密码，给出了基于XOR运算的视觉密码方案(XOR-based VCS, XVCS)的定义，其(,)方案的像素扩展度为1且对比度为1，可以实现秘密图像的完全恢复，远远优于(,)-OVCS。在实际应用中， XOR运算在解密时需要借助于计算机或光学设备。随着具有简单计算能力的智能终端如手机、PAD等的日益普及，为执行XOR运算提供了一种有效途径。考虑到“XOR”和“OR”运算的计算机复杂度的阶数相等，因而XOR运算可以很好地平衡解密运算和方案的参数。然而，由于XOR运算存在反转特性，文献[17]指出上述基于XOR运算的方案只能用于分享一幅秘密图像，运用到现有矩阵拼接设计法中，会产生部分区域无法正确恢复的问题，因而不能直接应用于RIVCS。

针对上述问题，本文依据共享份分块构造的设计思路，依据授权子集的个数将共享份划分成若干部分，分多次生成共享份的不同部分，各部分的构造之间独立，对于解密区域利用单秘密XVCS进行构造，对于未解密区域填充随机数实现遮盖，可以解决XOR运算不适用于RIVCS的问题，在此基础上，设计了一种异或区域递增式视觉密码方案(XOR-based Region Incrementing Visual Cryptography Scheme, XRIVCS)的秘密分享与恢复流程，最后对方案的有效性进行了理论证明和实验验证。

2 基本概念

为方便描述，文中所用符号及函数的含义见表1。

表1 本文所用符合及其含义

定义2[12]记参与者集合为，称能够恢复秘密图像的参与者集合为授权子集，不能恢复秘密图像的参与者集合为禁止子集。记表示所有授权子集的集合，表示所有禁止子集的集合，则,，且,，称为参与者集合之上的存取结构。(,)门限结构是一类特殊的存取结构，满足,。

定义3[13]称两个以布尔矩阵为元素的集合和，组成一个(,)-XVCS。是分享白像素的映射空间，是分享黑像素的映射空间，在分享白(黑)像素时从中随机选取一个矩阵，对应个共享份各自的个子像素。满足以下两个条件。

条件(1)是对比性条件，表明当参与者人数等于个时，通过异或运算能够恢复秘密图像。条件(2)是安全性条件，表明当参与者人数小于个时，得不到秘密图像的任何信息。表示恢复图像中原白像素对应子像素块的最大汉明重量，表示恢复图像中原黑像素对应子像素块的最小汉明重量。m称为像素扩展度，表示1个原像素被分享成为共享份中的个子像素，其越小越好。称为对比度，表示恢复图像与原图像在视觉上的差别，其越大越好。当=1且=1时，恢复图像相对于原图像无失真，称该视觉密码方案是完全恢复的。令为-XVCS的加密矩阵集合，则由所有汉明重量为偶数的维列向量组成，由所有汉明重量为奇数的维列向量组成。

定义4 记表示参与者总数，表示秘密恢复门限值，满足，秘密图像S划分了个区域。

3 方案设计

基本思想是分次生成共享份的各个部分，然后将各部分进行拼接得到最终的共享份，拼接的方式不受限制，既可以是行向拼接，也可以是纵向拼接，或者按矩形拼接，各部分的位置和顺序也不受限制。秘密恢复方法与以往RIVCS相同，只需要将满足条件的共享份异或运算就可以恢复对应密级区域。

3.1 秘密分享流程

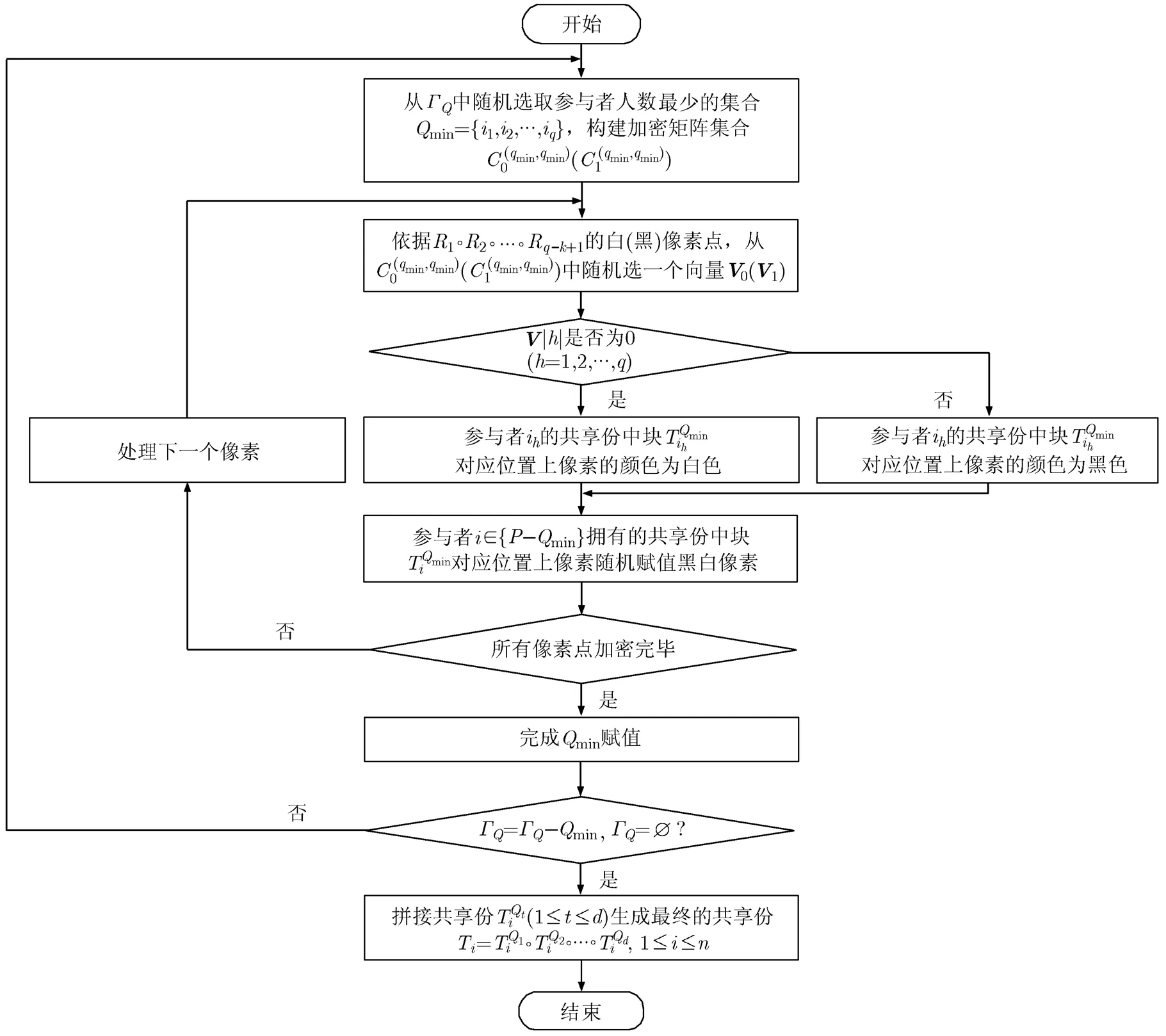
图1 共享份生成流程

具体步骤如表2所示。

表2共享份生成算法

3.2 秘密恢复流程

则在恢复图像()中能够显示相应密级区域。

4 有效性证明

引理1[13](,)-XVCS的加密矩阵集合由所有汉明重量为偶数的维列向量组成，由所有汉明重量为奇数的维列向量组成。

命题1 若秘密图像中各密级区域大小相等，则(,)-XRIVCS的像素扩展度为

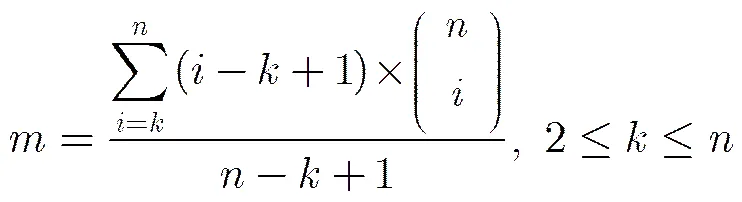
证明 本文方案的像素扩展度与秘密图像中各区域大小所占比例有关，这里仅考虑各区域大小相等的情况。设秘密图像S的大小为，对于(,)门限结构，S被划分了个区域，则单个区域的大小为。由秘密分享流程可知，方案依据授权子集分块构造共享份的各部分，其中授权子集生成部分的大小与相等，即。对于包含了个参与者的授权子集，满足此条件的集合的个数为。因此，共享份的像素扩展度为

5 实验与分析

下面给出本文方案的一个实例，以(2,3)- XRIVCS为例，依据方案流程进行实验仿真，秘密图像S包含两个区域1=和2=。

需要(2, 2)-XVCS, (3, 3)-XVCS的加密矩阵集合。

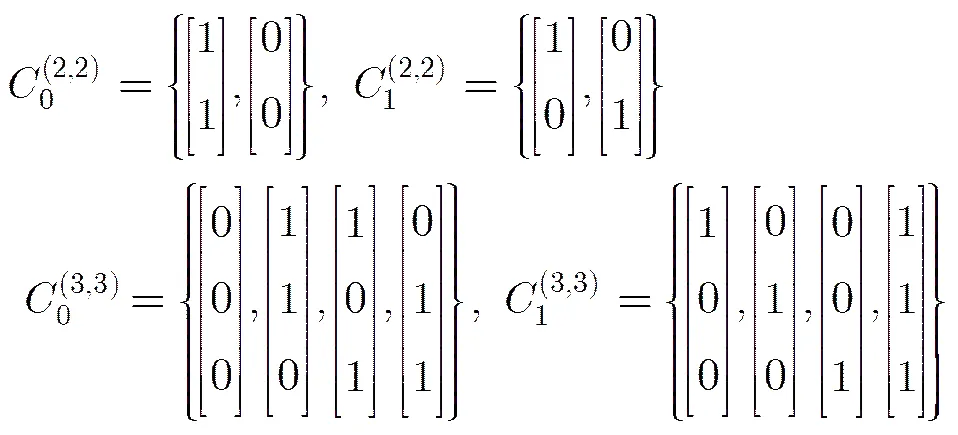
按照秘密分享与恢复流程，生成的共享份和恢复的秘密图像如图2所示，分析实验结果可知：

图2 (2, 3)-RIVCS的实验效果

(1)单个共享份是杂乱无章的，无法看到任何区域的秘密信息；

(2)任意2个共享份进行XOR运算后，区域1实现了完全恢复；

(3)3个共享份进行XOR运算后，区域1和2都实现了完全恢复，与预期结果相同。

本文方案与其他区域递增式视觉密码方案的比较见表3和表4。

表3本文方案与文献[5-8]的像素扩展度比较

注：-表示不存在。

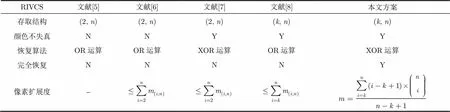
表4本文方案与其他区域递增式视觉密码方案的比较

注：N为否，Y为是，-为无具体表达式。

(1)在存取结构方面，文献[8]和本文方案适用于任意(,)门限结构，应用范围更丰富。

(2)在颜色失真方面，文献[7, 8]和本文方案不存在颜色反转失真，因而恢复图像可以正确显示原始图像颜色的真实信息。

(3)在恢复算法方面，本文方案适用于XOR运算，由于XOR运算不违背视觉密码恢复简单性的原则，随着具有简单计算能力的智能终端的普及，基于XOR运算的方案使用将更加方便，应用前景更加广阔。

(4)在完全恢复方面，本文方案在实现区域递增式显示效果的前提下，能够完成各区域图案的完全恢复，因此恢复效果最佳。

6 结束语

本文对区域递增式视觉密码进行了研究，给出了一种解密区域完全恢复方案的构造方法，并对方案的有效性进行了理论证明。本文方案通过对共享份进行分块构造，并结合异或单秘密视觉密码方案的加密矩阵，设计了秘密图像的分享和恢复流程，为区域递增式视觉密码的研究提供了一条新思路。

参考文献

[1] 付正欣, 郁滨, 房礼国. 一种新的多秘密分享视觉密码[J]. 电子学报, 2011, 39(3): 712-718.

Fu Zheng-xin, Yu Bin, and Fang Li-guo. A new multi-secret sharing visual cryptography[J]., 2011, 39(3): 712-718.

[2] 付正欣, 郁滨, 房礼国. 基于压缩算法的存取式多秘密视觉密码[J]. 电子与信息学报, 2013, 35(5): 1055-1062.

Fu Zheng-xin, Yu Bin, and Fang Li-guo. The access-based multi-secret visual cryptography with compression algorithm[J].&, 2013, 35(5): 1055-1062.

[3] Yu B and Shen G. Multi-secret visual cryptography with deterministic contrast[J]., 2014, 72(2): 1867-1886.

[4] Shyu S J and Jiang H W. General constructions for threshold multiple-secret visual cryptography schemes[J]., 2013, 8(5): 733-743.

[5] Wang R Z. Region incrementing visual cryptography[J]., 2009, 16(8): 659-662.

[6] Shyu S J and Jiang H W. Efficient construction for region incrementing visual cryptography[J]., 2012, 22(5): 769-777.

[7] Yang C N, Shih H W, Chu Y Y,.. New region incrementing visual cryptography scheme[C]. Proceedings of the International Conference on Image Processing, Computer Vision, and Pattern Recognition in Conjunction with WORLDCOMP, LasVegas, USA, 2011: 323-329.

[8] Yang C N, Shih H W, Wu C C,..out ofregion incrementing scheme in visual cryptography[J]., 2012, 22(5): 799-810.

[9] Yang C N, Lin Y C, and Wu C C. Region-in-Region incrementing visual cryptography scheme[C]. Proceedings of 12th International Workshop on Digital-Forensics and Watermarking, Auckland, New Zealand, 2013 (LNCS 7809) 449-463.

[10] Chen Y C, Tsai D S, and Horng G. A new authentication based cheating prevention scheme in Naor-Shamir’s visual cryptography[J]., 2012, 23(8): 1225-1233.

[11] Naor M, and Shamir A. Visual cryptography[C]. Proceedings of the Advances in Cryptology-Eurocrypt’94, Berlin, 1995 (LNCS 950): 1-12.

[12] Ateniese G, Blundo C, Santis A D,.. Visual cryptography for general access structures[J]., 1996, 129(2): 86-106.

[13] Tuyls P, Hollmann H D L, Lint J H V,.. XOR-based visual cryptography schemes[J]., 2005, 37(1): 169-186.

[14] Wang D S, Zhang L, Ma N,.. Two secret sharing schemes based on Boolean operations[J]., 2007, 40(10): 2776-2785.

[15] Liu F, Wu C, and Lin X. Step construction of visual cryptography schemes[J]., 2010, 5(1): 27-38.

[16] Wu X and Sun W. Random grid-based visual secret sharing with abilities of OR and XOR decryptions[J]., 2013, 24(1): 48-62.

[17] Yang C and Wang D S. Property analysis of XOR based visual cryptography[J]., 2014, 24(2): 189-197.

XOR-based Region Incrementing Visual Cryptography Scheme with Share Block Construction

Yu Bin①Hu Hao①Chen Wu-ping②Shen Gang①

①(,450001,)②(,100072,)

By designing the block construction for each share, which is divided into several blocks according to the number of qualified sets, the secret sharing and recovering algorithms of the XOR-based region incrementing visual cryptography are designed with the encoding matrices of the (,) XOR-based single secret sharing visual cryptography. Comparing with the existing schemes, the proposed scheme realizes the perfect recovery of decoded regions in secret image, and the sizes of shares are also decreased efficiently.

Visual cryptography; Region incrementing; Security level; Block construction; XOR operation; Perfect recovery

TP309.7

A

1009-5896(2015)08-1978-06

10.11999/JEIT141385

胡浩 wjjhh_908@163.com

2014-10-31收到，2015-02-04改回，2015-05-11网络优先出版

国家自然科学基金(61070086)和信息保障技术重点实验室开放基金(KJ-13-107)资助课题

郁滨： 男，1964 年生，博士，教授，博士生导师，研究方向为视觉密码和网络安全.

胡浩： 男，1989 年生，硕士生，研究方向为视觉密码.

陈武平： 男，1964 年生，博士，高级工程师，研究方向为信息安全.

沈刚： 男，1986 年生，博士生，研究方向为视觉密码.