基于Pro/E的圆弧弯曲钢丝绳建模理论及几何实现

郭　卫　路正雄　张　武

西安科技大学，西安，710054

基于Pro/E的圆弧弯曲钢丝绳建模理论及几何实现

郭卫路正雄张武

西安科技大学，西安，710054

为了精确建立多股圆弧弯曲钢丝绳空间实体模型，对双螺旋钢丝绳各钢丝空间几何位置关系进行了分析，运用空间坐标变换理论建立了圆弧弯曲钢丝绳数学模型，推导出圆弧弯曲钢丝绳各钢丝中心线的参数方程，结合Pro/E的参数化建模和曲面造型功能，完成了6×7IWS圆弧弯曲钢丝绳几何模型的建立。所获结论为弯曲状态螺旋钢丝绳数学模型的建立奠定了理论基础，为圆弧弯曲状态下钢丝绳的弹性特性理论分析提供了可能。

多股圆弧弯曲钢丝绳；坐标变换理论；数学建模；实体建模

0　引言

钢丝绳是一种柔性螺旋结构钢制品[1]，具有强度高、绕性好、耐冲击等特点，在使用中具有传动平稳、承载力大、工作可靠等优点，被广泛应用于矿山生产、机械加工、交通、建筑、桥梁、航空和航天等领域[2]。在实际工况下，钢丝绳一般存在直立和弯曲两种物理状态，有时甚至出现多个弯曲段[3]。这使钢丝绳的变形、受力变得十分复杂，尤其是在弯曲段[4-6]，因此，精确的弯曲钢丝绳模型对于其力学特性分析就显得十分重要。

关于直立状态钢丝绳建模，国内外学者做了大量的研究工作。孙建芳等[7]分析了在考虑接触摩擦时钢丝绳的成形过程；王桂兰等[8]、Lee等[9-10]基于微分几何学的Frent标架理论，给出了直立时二次螺旋线的数学表达式；Erdönmez[11]基于微分几何学理论，将直立状态钢丝绳钢丝的数学表达式由二次螺旋线推广到n次螺旋线；Stanova等[12]运用空间坐标变换理论，建立了直立状态钢丝绳的数学模型。然而，在弯曲状态钢丝绳建模方面研究成果较少。Hobbs等[13]和Nabijou等[14]基于微分几何学理论，以直立钢丝绳数学模型为基础，给出了钢丝在绳轮上的路径表达式；李晓豁等[15]在此理论基础上进行了几何建模，但复杂结构钢丝绳模型的建立仍不完善。本文在上述学者的研究基础上，运用空间坐标变换理论，系统地阐述了圆弧弯曲双螺旋钢绳的建模过程，并给出了圆弧弯曲状态下各螺旋钢丝中心线曲线方程及其几何模型。

1　钢丝绳结构

双螺旋钢丝绳由多根钢丝按照一定空间螺旋线关系缠绕而成，一般由多股螺旋缠绕中心股而成，股的绕制方向为绳的捻向；每股又由多层钢丝螺旋环绕该股芯丝而成，丝的绕向即为股的捻向,如图1所示。钢丝作为构成股和绳的基本元素，在空间一般以四种几何形式存在(图2)：中心股芯丝中心线，该线一般为直立或简单曲线；中心股侧丝中心线，其相对于中心股中心线为一次螺旋线；侧股芯丝中心线，该线相对于中心股芯丝中心线是一次螺旋曲线；侧股侧丝中心线，该线相对于中心股中心线是二次螺旋线。为生成股中各钢丝的空间螺旋曲线，必须建立各钢丝中心线的数学方程。

图1　二次捻制钢丝绳示意图图2　双螺旋钢丝绳断面图

2　圆弧弯曲钢丝绳数学模型

2.1圆弧弯曲钢丝绳中心股钢丝数学模型

钢丝绳在使用过程中，受工况影响，对安全系数和绳径比(绳轮直径与钢丝绳直径的比值)有不同的要求[16]。按右手法则建立笛卡尔坐标系Oxyz，作为钢丝绳数学模型的全局坐标系，建立钢丝绳数学模型。

2.1.1中心股芯丝

中心股芯丝中心线是以S(0,R1,0)为起点绕x轴逆时针旋转γ(0≤γ≤π)角度所得的圆弧，完成此变换的旋转矩阵如下：

(1)

图3所示为中心股芯丝中心线。

图3　中心股芯丝中心线

中心股芯丝参数方程为

(2)

2.1.2中心股侧丝

设中心股右旋，该股第j层侧丝螺旋角为Φj，在起始位置处，侧丝中心线上某动点的齐次坐标为(rj,R1,0,0)，其中，rj为动点的螺旋半径。中心股侧丝的螺旋运动可由多个矩阵变换实现。首先，将全局坐标系Oxyz按向量u=(0,R1,0,0)平移得坐标系Sx1y1z1，并使z1轴与中心线在点S处相切，变换过程中所需要的矩阵T1为

(3)

然后，通过如下的矩阵T2使动点绕z1轴逆时针旋转θ角：

(4)

设β、Φj分别为一次螺旋线的捻角和螺旋角，根据中心股丝之间的几何关系得

(5)

从而有

(6)

令

(7)

故

θ=c γ

其中，c为一次螺旋线绕中心线绕制的圈数。

为获得一次螺旋线在全局坐标系Oxyz中的螺旋线轨迹，必须先经如下的平移变换矩阵T3进行变换:

(8)

最后，通过如下的矩阵T4完成一次螺旋线绕中心股芯丝中心线在Oxyz坐标系中的旋转变换:

(9)

所以，总变换矩阵为

(10)

在坐标系Oxyz中，一次螺旋线用矩阵表示为

[xyz1]T=T[rjR101]T

(11)

在全局坐标系Oxyz中，一次螺旋线的参数方程表示为

(12)

假设钢丝绳绳股第j层有mj根钢丝，式(12)为第j层中第i根钢丝的中心线方程。其他侧丝中心线方程只需将第i根侧丝中心线绕芯丝中心线逆时针旋转ξji=(i-1)2π/mj角度即可，其中i=1，2,…,mj。该旋转变换矩阵为T5，股中各钢丝间关系如图4所示。

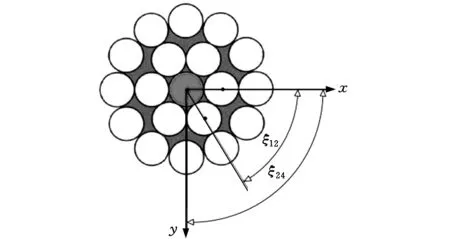
图4　股中各丝相对位置关系示意图

变换矩阵T5的表达式为

(13)

综上所述，一次螺旋线变换矩阵为

T=T4T3T2T5T1

(14)

中心股第j层任意侧丝中心线参数方程为

(15)

弯曲钢丝绳中心股侧丝的螺旋线方程为

(16)

其中，当q=1时，圆弧弯曲钢丝绳中心股侧丝右旋；当q=-1时，圆弧弯曲钢丝绳中心股侧丝左旋。

图5　弯曲钢丝绳中心股中心线图

式(16)为圆弧弯曲钢丝绳中心股侧丝中心线参数方程，通过式(15)可得到6×7IWS圆弧弯曲钢丝绳右旋中心股芯丝中心线图，如图5所示。

2.2圆弧弯曲钢丝绳侧股钢丝数学模型

2.2.1圆弧弯曲钢丝绳侧股芯丝数学模型

圆弧弯曲钢丝绳侧股芯丝相对于中心股芯丝仍为一次螺旋线，其参数方程为

(17)

式中，R为侧股芯丝螺旋半径；m为股数。

2.2.2圆弧弯曲钢丝绳侧股侧丝数学模型

假设侧股侧丝左旋，侧股第j层侧丝螺旋角为Ψj，二次螺旋线上某动点在起始位置处的齐次坐标为(R+rj,R1,0,1)，rj为动点的螺旋半径。按矩阵T1平移坐标系Oxyz，使z轴在点S处与中心股芯丝中心线相切。将平移所得坐标系Sx1y1z1绕x1轴顺时针旋转β角度，同时平移向量v=(R,0,0,0)，使z1轴与一次螺旋线起点相切，该组合变换矩阵为

(18)

通过如下的旋转矩阵T7使动点绕z2轴顺时针旋转角度φ：

(19)

图6为侧股侧丝中心线、侧股芯丝中心线及中心股芯丝中心线沿捻向展开的示意图。

图6　侧股侧丝、芯丝及中心股芯丝沿捻向展开图

设α、β分别为股的捻角和钢丝绳的捻角，取任意一段股长，由圆弧弯曲钢丝绳几何关系得φ与θ关系：

(20)

令

有

φ=c1θ

(21)

式中，c1为二次螺旋线绕一次螺旋线绕制的圈数。

由式(6)和式(20)得γ与φ之间的关系为

(22)

为获得动点在坐标系Oxyz中的参数方程，必须先进行坐标变换T8，求得二次螺旋线在坐标系Sx1y1z1中的方程。T8表达式为

(23)

通过如下的矩阵T9完成动点绕侧股芯丝的右旋：

(24)

通过矩阵T3对坐标系Sx1y1z1进行平移，动点通过矩阵T4沿中心股芯丝转动。因此，动点总坐标变换矩阵表示为

T′=T4T3T9T8T7T6T1

(25)

坐标系Oxyz中动点坐标的矩阵方程为

(26)

弯曲钢丝绳侧股侧丝中心线参数方程为

(27)

若弯曲钢丝绳侧股第j层有mj根钢丝，式(27)为第i根侧丝的中心线方程，其他侧丝中心线只需将第i根钢丝的中心线绕芯丝中心线逆时针旋转ξji=(i-1)2π/mj，其中，i=1,2,…,mj，旋转矩阵为

(28)

侧股第j层任意钢丝的参数方程为

(29)

综上所述，圆弧弯曲钢丝绳侧股侧丝方程为

(30)

其中，当p=1时,若q=-1弯曲钢丝绳为右同向捻，q=1弯曲钢丝绳为右交互捻；当p=-1时，若q=1为左交互捻弯曲钢丝绳，q=-1为左同向捻弯曲钢丝绳。

式(29)为弯曲钢丝绳左旋侧股侧丝中心线的参数方程，由该方程得6×7IWS圆弧弯曲钢丝绳左旋侧股钢丝中心线图，如图7所示。

图7　圆弧弯曲钢丝绳侧股中心线图

式(30)为圆弧弯曲钢丝绳的数学模型，由该方程得右交互捻圆弧弯曲钢丝绳钢丝中心线图，如图8所示。

图8　圆弧弯曲钢丝绳钢丝中心线图

3　弯曲钢丝绳几何模型

以6×7IWS右交互捻钢丝绳为例，运用Pro/E软件和数学模型完成圆弧弯曲钢丝绳几何模型的建立。取绳径比为20，绳和股的几何参数如表1、表2所示。

表1　6×7IWS钢丝绳结构参数

表2　6×7IWS钢丝绳股结构参数

6×7IWS圆弧弯曲钢丝绳由6个相同侧股和一个中心股螺旋绕制而成；每股由6根侧丝螺旋缠绕一根中心钢丝而成，每根钢丝的直径相同。运用Pro/E的参数建模及曲面建模功能，完成圆弧弯曲钢丝绳中心股的几何建模，如图9所示。圆弧弯曲钢丝绳侧股三维模型如图10所示，圆弧弯曲钢丝绳整体三维模型如图11所示。

图9　弯曲钢丝绳中心股三维模型

图10　弯曲钢丝绳侧股三维模型

图11　弯曲钢丝绳整体三维模型

4　结论

(1)本文分析了一次和二次螺旋钢丝在钢丝绳中的几何位置关系，系统阐述了钢丝绳绕制成形过程。

(2)运用微分几何理论和空间坐标变换理论，建立了定绳径比单/多股多层圆弧弯曲钢丝绳数学模型。

(3)运用Pro/E软件的参数化建模和曲面造型功能，完成了绳径比为20时6×7IWS右交互捻圆弧弯曲钢丝绳几何模型的建立。

(4)本研究结论为其他弯曲状态螺旋钢丝绳数学模型的建立奠定了理论基础，为圆弧弯曲状态下钢丝绳力学特性分析提供了可能。

[1]Velinsky S A. Design and Mechanics of Multi-lay Wire Strand[J].Journal of Mechanical Design,1988,110(2): 152-160.

[2]五弓勇雄.金属塑性加工金属[M].陈天忠，张国荣,译.北京：冶金工业出版社，1987.

[3]张钫,张平萍.影响钢丝绳弯曲疲劳试验因素的分析[J].金属制品，2006,32(3):46-47.

Zhang Fang, Zhang Pingping. Analysis of Effect Factors on Bend and Fatigue Test of Steel Wire Rope[J]. Steel Wire Products,2006,32(3):46-47.

[4]Jiang W G, Henshall J L,Walton J M.A Concise Finite Element Model for Three-layered Straight Wire Rope Strand[J]. International Journal of Mechanical Sciences,2000,42(1): 63-86.

[5]马军，葛世荣，张德坤.钢丝绳股内钢丝的载荷分布[J].机械工程学报，2009，45(4)：259-264．

Ma Jun,Ge Shirong,Zhang Dekun. Load Distribution on the Unit of the Wire Rope Strand[J].Journal of Mechanical Engineering,2009,45(4):259-264．

[6]马军,葛世荣,张德坤.钢丝绳应力及股内钢丝变形的相关性研究[J]. 煤炭科学技术,2009,3:73-76.

Ma Jun,Ge Shirong,Zhang Dekun. Research on Relativity between Steel Cable Stress and Steel Wire Deformation of Strand[J]. Coal Since and Technology, 2009,3:73-76.

[7]孙建芳,王桂兰,张海鸥.考虑接触摩擦的金属捻线捻制成形过程计算机模拟[J].系统仿真学报,2005,17(7): 1746 -1750.

Sun Jianfang, Wang Guilan, Zhang Haiou. Nume- rical Simulation for Laying Wire Rope with Friction Contact[J].Journal of System Simulation,2005,17(7): 1746 -1750.

[8]王桂兰,赵瑞敏,孙建芳,等.基于微分几何学的钢丝绳结构CAD[J].华中科技大学学报(自然科学版)，2003,31(6):4-6.

Wang Guilan,Zhao Ruimin,Sun Jianfang.CAD of Wire Rope Structure Based on the Differential Geometry[J].J. Huazhong Univ. of Sci. & Tech. (Natural Science Edition), 2003,31(6):4-6.

[9]Lee W K, Casey N F,Gray T G F.Helix Geometry in Wire Rope[J].Wire Ind.,1987,54(8): 461-468.

[10]Lee W K. An Insight into Wire Rope Geometry[J]. International Journal of Solids and Structure,1991,28(4):471-490.

[11]Erdönmez C. N-tuple Complex Helical Geometry Modeling Using Parametric Equations[J].Engineering with Computers, 2014，30(5):715-726.

[12]Stanova E, Fedorko G, Fabian M,et al. Computer Modeling of Wire Strands and Ropes Part I:Theory and Computer Implementation[J].Advances in Engineering Soft Ware,2011,42(6): 305-315.

[13]Hobbs R E, Nabijou S. Changes in Wire Curvature as a Wire Rope Is Bent Over a Sheave[J]. The Journal of Strain Analysis for Engineering Design, 1995,30(4): 271-281.

[14]Nabijou S,Hobbs R E.Relative Movements within Wire Ropes Bent over Sheaves[J].The Journal of Strain Analysis for Engineering Design,1995,30(2):155-165.

[15]李晓豁,张惠波,战林,等.天轮处提升钢丝绳的曲率和挠率分析[J].世界科技研究与发展,2012, 34(2): 198-200.

Li Xiaohuo,Zhang Huibo,Zhan Lin, et al.Analysis on Curvature and Torsion of Hoisting Rope Bent over Sheave[J].World Sci. Tech. R&D,2012, 34(2): 198-200.

[16]胡茂.滑轮直径对钢丝绳寿命影响研究[D].武汉：武汉理工大学,2012.

(编辑郭伟)

Geometric Modeling Theory of Bent Wire Rope Based on Pro/E

Guo WeiLu ZhengxiongZhang Wu

Xi’an University of Science and Technology,Xi’an,710054

In order to establish the bent model of multi-strands wire rope more exactly, the geometry relations of the various steel wires were analyzed about the bent wire rope in pace. Based on the theory of space alternate coordinate, the original parametric equation of the center line was deduced to the various steel wires in the bent wire rope. Using the capabilities of parametric and surface modeling of Pro/E, the solid modeling of the 6×7IWS bent wire rope was completed. The mathematical model of spiral steel wire rope lays a theoretical foundation for any bending wire rope and provides a possibility about theoretical analysis of the mechanical properties for the bent wire rope.

multi-strands bent wire rope; theory of space alternate coordinate; mathematical modeling;solid modeling

2014-11-27

中国博士后科学基金资助项目(2014M 562518XB)；西安科技大学培育基金资助项目(201330)

TH132DOI：10.3969/j.issn.1004-132X.2015.17.015

郭卫，男，1955年生。西安科技大学机械工程学院教授、博士研究生导师。主要研究方向为煤矿机械、矿山机械提升设备。发表论文50余篇。路正雄(通信作者)，男，1986年生。西安科技大学机械工程学院硕士研究生。张武，男，1985年生。西安科技大学机械工程学院讲师、博士后研究人员。