单腿跳跃机器人轨迹规划
2015-10-29王申江郭祖华
王申江 郭祖华
北京航空航天大学,北京,100191
单腿跳跃机器人轨迹规划
王申江郭祖华
北京航空航天大学,北京,100191
将单腿跳跃机器人简化成一个三杆模型,研究机器人跳跃过程中各个关节的运动轨迹问题,并在总结跳跃过程现有轨迹规划方法的基础上,运用参数化优化方法实现关节空间的轨迹规划,优化目标为机器人关节的控制势最小。将跳跃过程分解成开始段、腾空段、站立段和结束段,并对各段的关节轨迹分别优化,最后得到从静止状态开始起跳到着地后恢复至静止状态的整个跳跃过程的关节轨迹。
跳跃机器人;ZMP;优化;轨迹规划
0 引言
相比于轮式及履带式移动机器人,仿人机器人运动灵活,对地面要求低,对环境适应性强,因而倍受人们青睐。跳跃是仿人机器人的一种重要运动方式,可以极大地增加机器人的越障能力,在跳跃运动的不同阶段,机器人的运动状态和约束条件有很大的变化,但机器人的运动必然满足特定指标的最优性,所以本文采用优化的方法来寻找符合动力学约束的机器人跳跃轨迹。
当前跳跃机器人研究模型主要有三大类:第一类是仿生机器人,即从自然界生物的弹跳动作中获得启发,采用外形和功能与某类动物类似的机构实现跳跃功能。如瑞士的研究人员设计了一款类似蚱蜢的跳跃机器人,质量仅7g[1];Chen等[2]设计的蚱蜢跳跃机器实现了三倍自身高度的跳跃,而且能够完成自我姿态恢复;麻省理工学院研制了一种液压控制的仿袋鼠单腿跳跃机器人Uniroo[3];日本东京大学科研人员在Uniroo基础上进行了改进,研制了类似狗腿型的机器人Kenken[4]。第二类是简化模型,即直接利用简单机构产生弹跳力实现机器人的跳跃,这种机构自由度少,动力学模型简单,实现起来相对容易。如Cherouvim等[5]设计了两自由度的跳跃机器人,该机器人只包含身体和可伸缩腿,运用其设计的控制方法实现了机器人在未知的不平整地面上的跳跃。第三类是特殊驱动的弹跳机器人,如采用爆炸力来实现弹跳的机器人[1]。这些研究主要集中在机器人弹跳功能的实现上。
目前仿人机器人跳跃行为的轨迹规划主要包括两种:一是分析法。该方法是在满足动态稳定性约束前提下,根据设定的跳跃参数和机器人的结构参数,确定跳跃过程中机器人各关节的运动轨迹[6-8]。二是基于优化的方法,即以机器人动力学模型和稳定性条件为约束,采用优化的方法寻找最优的轨迹。该方法的主要目标是提高能量效率或是动态稳定性[9-11]。按轨迹的描述方法来划分,又可将轨迹规划问题分为参数化轨迹规划和非参数化轨迹规划。
目前的文献中大多只对腾空段和站立段进行了轨迹规划,只是得到了需要的起跳状态和着地状态而忽略了是否能够达到这些需要的状态,即没有考虑到机器人从静止状态能否达到需要起跳的状态以及能否从需要的着地状态达到静止状态。为了避免文献中优化参数个数和能量效率的矛盾,本文分析了有脚三杆机器人从静止直立开始到静止直立结束的全部过程,运用参数化优化的方法,在较少的优化参数条件下获得了控制势最小的最优轨迹。
1 三杆机器人模型
1.1机器人运动学和动力学
本文采用的仿人机器人简化模型如图1所示,机器人由三根连杆和脚组成,各部分间由转动关节连接,由下至上分别是脚、踝关节、小腿、膝关节、大腿、髋关节和躯干。研究机器人跳跃时,只考虑机器人在前向平面内的运动,每个关节有一个转动自由度。简化机器人模型的具体参数如表1所示,从小腿到躯干对各杆和各关节进行编号,各参量含义如下:mi(i=1,2,3)为第i杆的质量,Ii为第i杆绕其质心的转动惯量,li为第i杆的杆长,ri为第i杆质心距其较低端端点的距离占其杆长的比例;lf1、lf2分别为脚后跟和脚尖到脚踝的距离;θil、θiu分别为第i个关节角角度的最小值及最大值,其中θ23=θ2-θ3;τil、τiu分别为第i个关节力矩的最小及最大值。脚的质量忽略不计,且假设腾空过程中脚一直与地面保持平行。
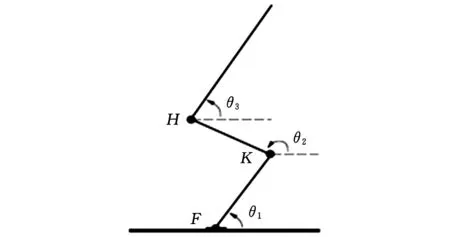
图1 跳跃机器人模型
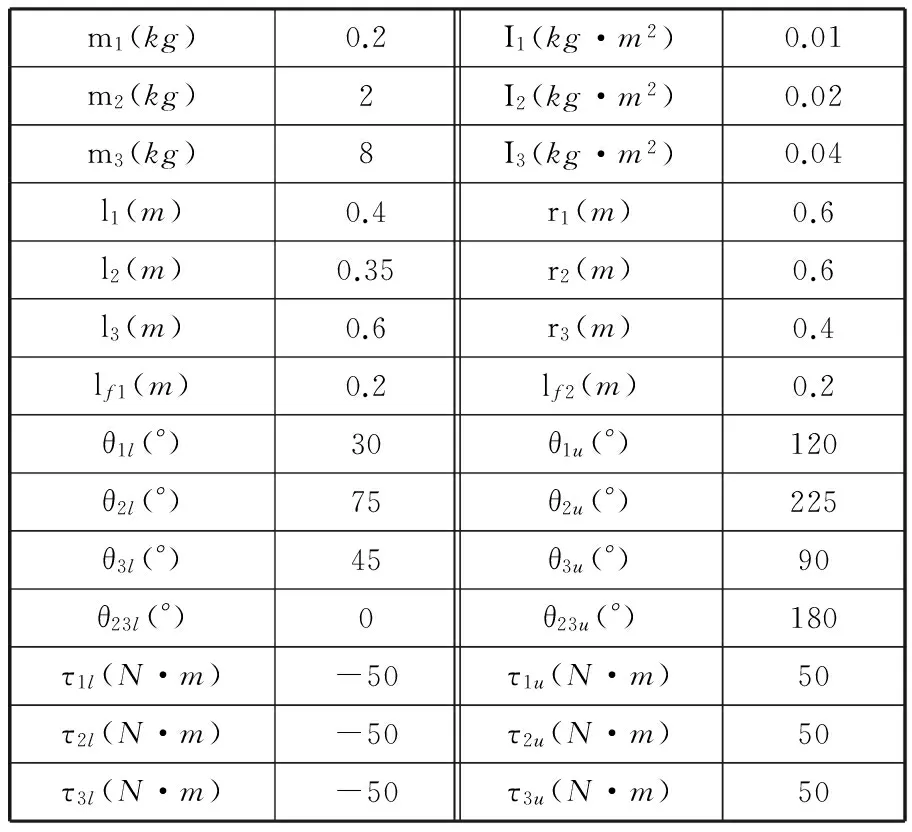
m1(kg)0.2I1(kg·m2)0.01m2(kg)2I2(kg·m2)0.02m3(kg)8I3(kg·m2)0.04l1(m)0.4r1(m)0.6l2(m)0.35r2(m)0.6l3(m)0.6r3(m)0.4lf1(m)0.2lf2(m)0.2θ1l(°)30θ1u(°)120θ2l(°)75θ2u(°)225θ3l(°)45θ3u(°)90θ23l(°)0θ23u(°)180τ1l(N·m)-50τ1u(N·m)50τ2l(N·m)-50τ2u(N·m)50τ3l(N·m)-50τ3u(N·m)50
(1)
其中,Θ=[θ1θ2θ3]T,f表示脚和质心的位置关系。
一般保守力系的拉格朗日方程为
(2)
q=[θ1θ2θ3xy]T
其中,L为拉格朗日函数或动势;q为选取的广义坐标;Q为各广义坐标对应的广义力;x、y为踝关节在惯性系中的坐标;τ1、τ2、τ3分别为三个在关节上施加的主动力矩;Fx、Fy为地面对脚的反作用力。
模型的动力学方程表述如下:
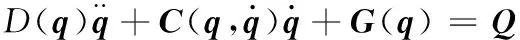
(3)
当机器人处在站立段时,采用ZMP作为稳定性判据,自ZMP判据提出至今,已经出现了许多不同的ZMP定义。概括起来主要有两类:一类从地面反力的角度出发,将地面反力向地面上某点等效,在该点处地面反力的力矩水平分量为零;另一类是指机器人机构上的重力与惯性力的合力的地面投影线的交点。按第二类定义,本文ZMP公式可以简化如下:
(4)
1.2碰撞模型

(5)
(6)
其中,J为雅可比矩阵,δF为冲击力在碰撞时间内的冲量,由式(5)和式(6)可以得到冲击后各个关节的角速度为
(7)
其中,I是和D同维数的单位矩阵。
2 参数化轨迹优化
2.1跳跃过程的分解
机器人的整个跳跃过程如图2所示,包含开始段(staringphase)、腾空段(flightphase)和站立段(stancephase)或停止段(stoppingphase)。开始段是机器人从静止直立状态到达离地前一时刻的状态(takeoff);腾空段是以脚离开地面开始,到脚再次与地面碰撞(touchdown)的前一刻结束;站立段从脚碰撞地面后一刻开始,到下一次腾空前结束;停止段从碰撞后一刻开始,到静止直立状态结束。
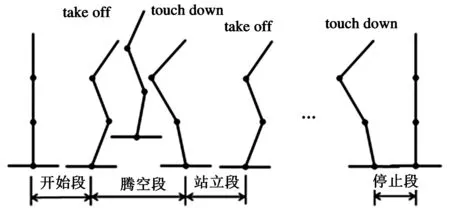
图2 机器人跳跃过程
2.2周期跳跃过程轨迹优化

(8)
(9)
腾空段踝关节不提供力矩,是一个欠驱动过程,三个关节角不是相互独立的。运用参数化方法假定关节角1和关节角2按如下规律进行变化:
θj(t)=aj1+aj2t+aj3t2+aj4t3+aj5t4+
aj6t5+aj7t3(t-tfl)3
(10)
j=1,2
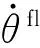
腾空段外力只有重力,所以其关于质心的角动量守恒。由此可得关系式
(11)
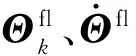
(12)
(13)
由式(10)~式(13)计算出所有关节角的角度、角速度和角加速度后,再由式(2)可以计算出每个采样时间内的膝关节和髋关节力矩τ2、τ3,踝关节力矩τ1=0。
机器人在腾空段的优化模型如下:
目标函数:
U=
[τ1(1)τ2(1)τ3(1)…τ1(N)τ2(N)τ3(N)]T
等式约束:
不等式约束:
τ2l≤τ2≤τ2uτ3l≤τ3≤τ3u
θil≤θi≤θiui=1,2,3
θ23l≤θ23≤θ23u

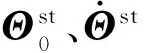
(14)
站立段是全驱动状态,假设三个关节角都按式(10)的规律变化,目标函数与腾空段相同,优化模型的约束如下:
等式约束:
不等式约束:
τ1l≤τ1≤τ1uτ2l≤τ2≤τ2u
τ3l≤τ3≤τ3uθil≤θi≤θiui=1,2,3
θ23l≤θ23≤θ23u-lf1≤xp≤lf2
Fy≥0Fx≤μFy
其中,lf1和lf2分别是脚后跟和脚尖到踝关节的距离,μ是地面滑动摩擦因数,文中取μ=2/3。
周期跳跃过程中三个关节角、角速度、关节力矩、ZMP随时间变化关系如图3~图6所示,从图中可以看出,整个过程中关节角连续变化,在碰撞时刻关节角速度产生突变。
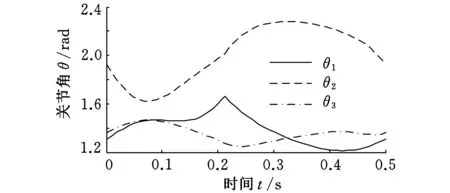
图3 周期过程的关节角变化

图4 周期过程的关节力矩变化
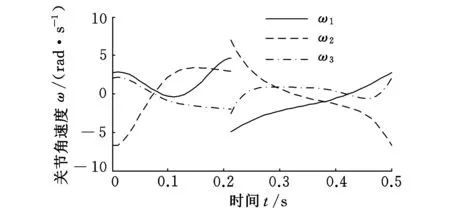
图5 周期过程的关节角速度变化
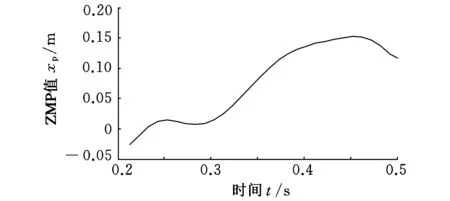
图6 周期过程的ZMP变化
2.3开始段以及停止段轨迹优化
开始段和停止段优化方法以及约束条件与周期过程的站立段相似,值得强调的一点是腾空段前向速度为vcx的取值不宜过大。从开始段来看,若vcx选取过大,机器人从静止直立状态到腾空前的状态,踝关节需要施加更大的力矩,容易导致机器人失稳。
图7~图10所示为开始段三个关节角、角速度、关节力矩、ZMP随时间的变化曲线,图11~图14为停止段各量的变化规律图。

图7 周期过程的关节角变化
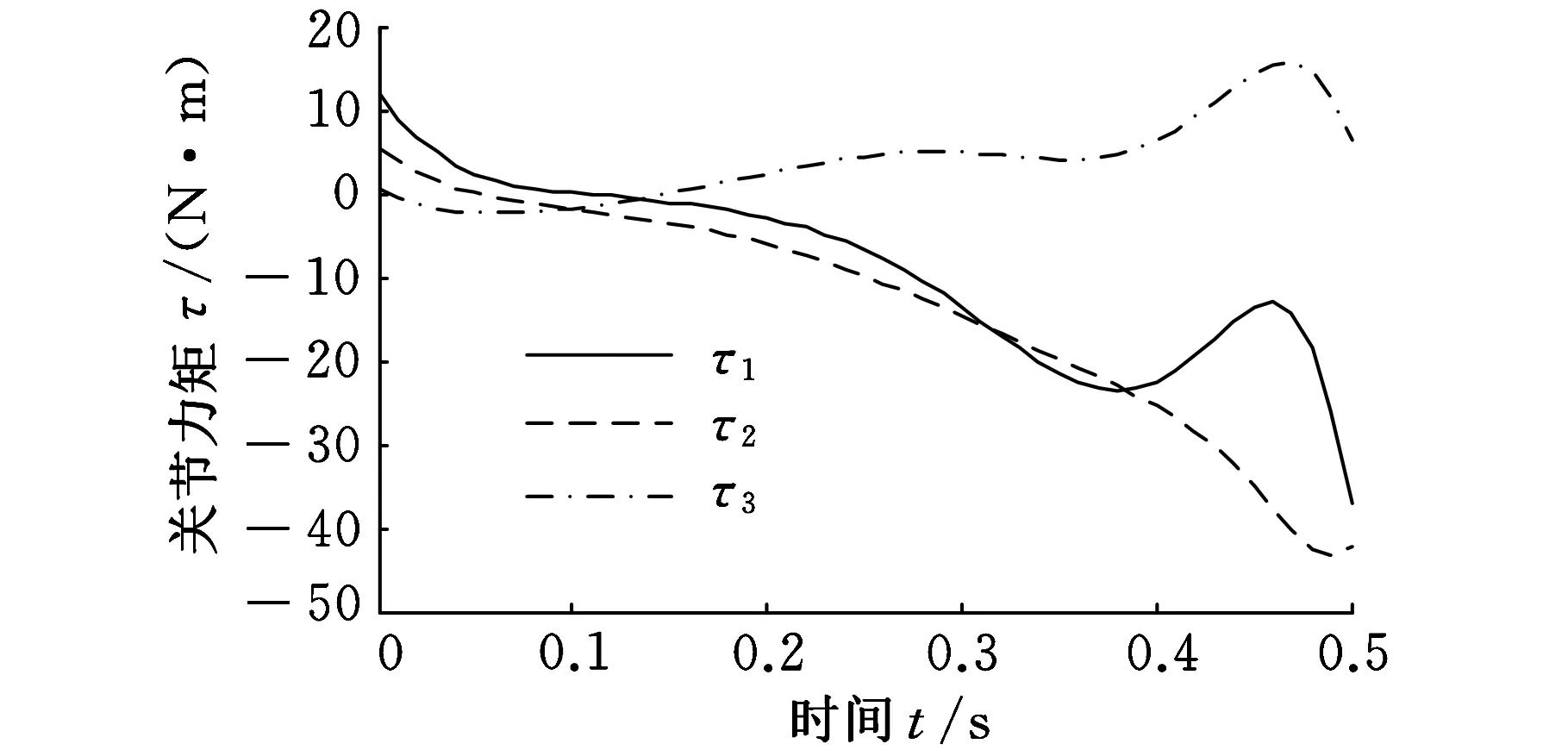
图8 周期过程的关节力矩变化

图9 周期过程的关节角速度变化

图10 周期过程的ZMP变化
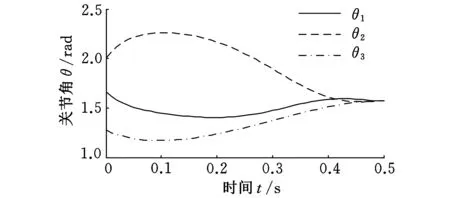
图11 周期过程的关节角变化

图12 周期过程的关节力矩变化
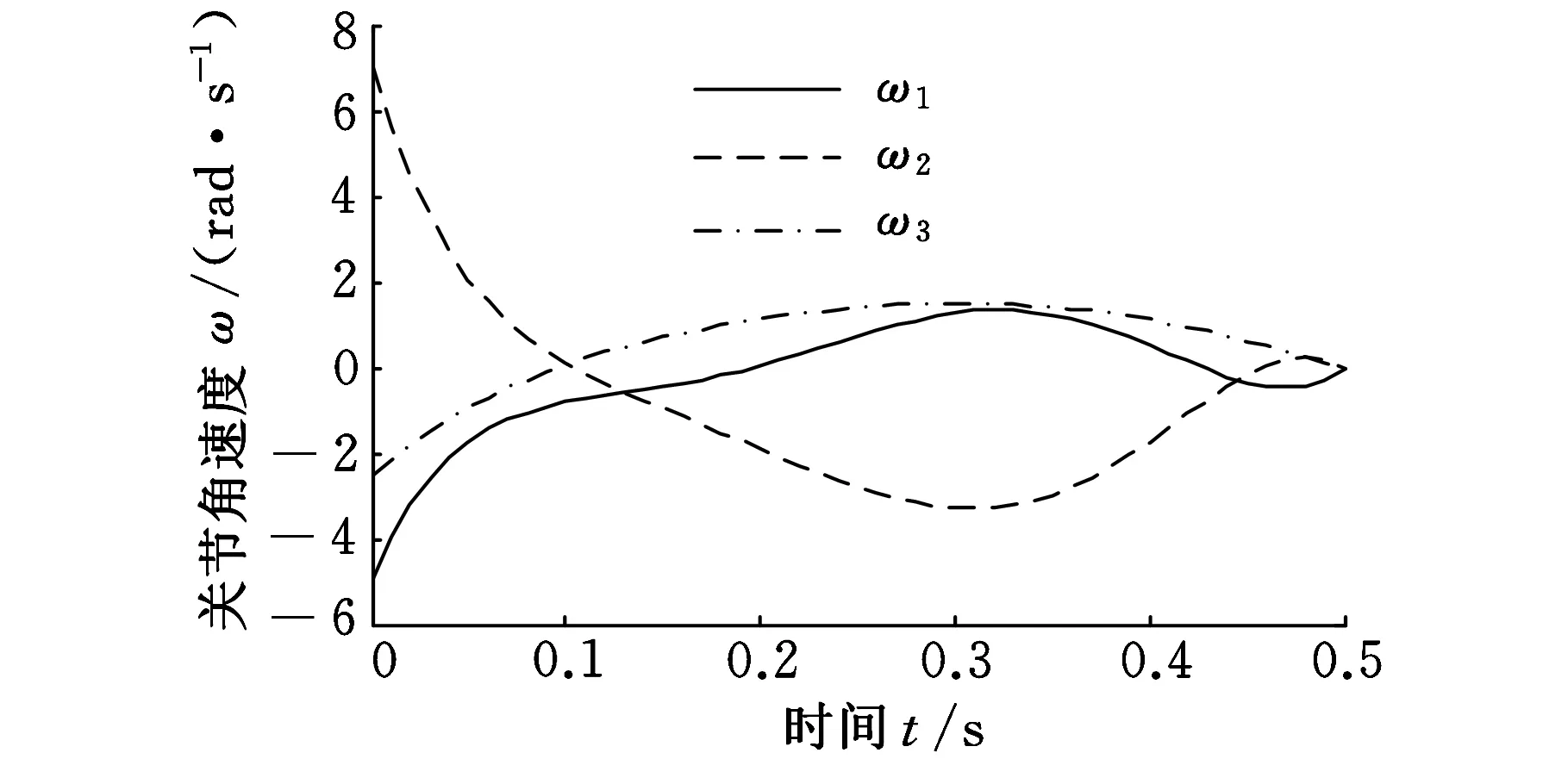
图13 周期过程的关节角速度变化
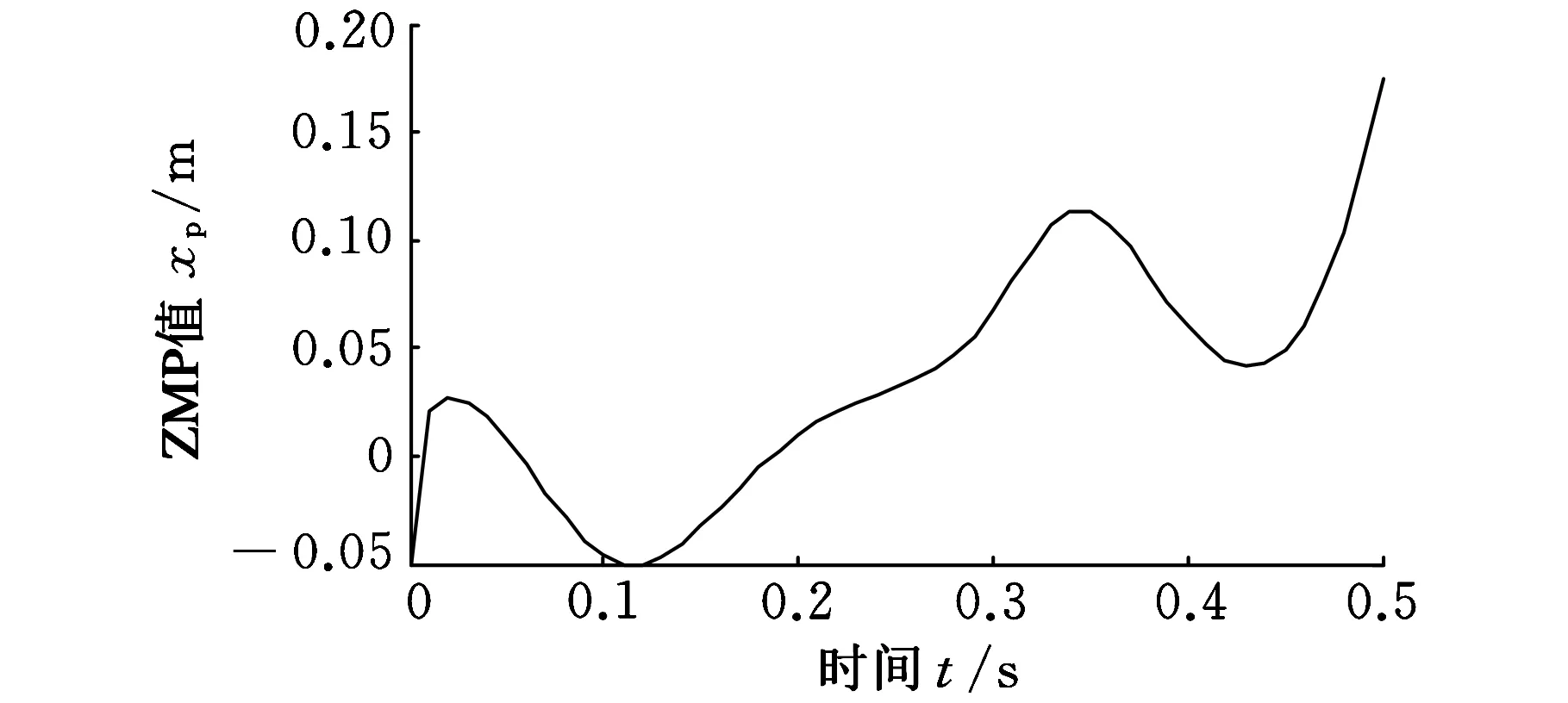
图14 周期过程的ZMP变化
对比站立段、开始段以及停止段的ZMP轨迹可知,在站立段和停止段ZMP变化范围较小,而开始段变化较大,特别是开始段取得的负值很大,一个可能的解释是开始段从静止加速到起跳状态,需要的踝关节力矩较大,导致ZMP负值很大。
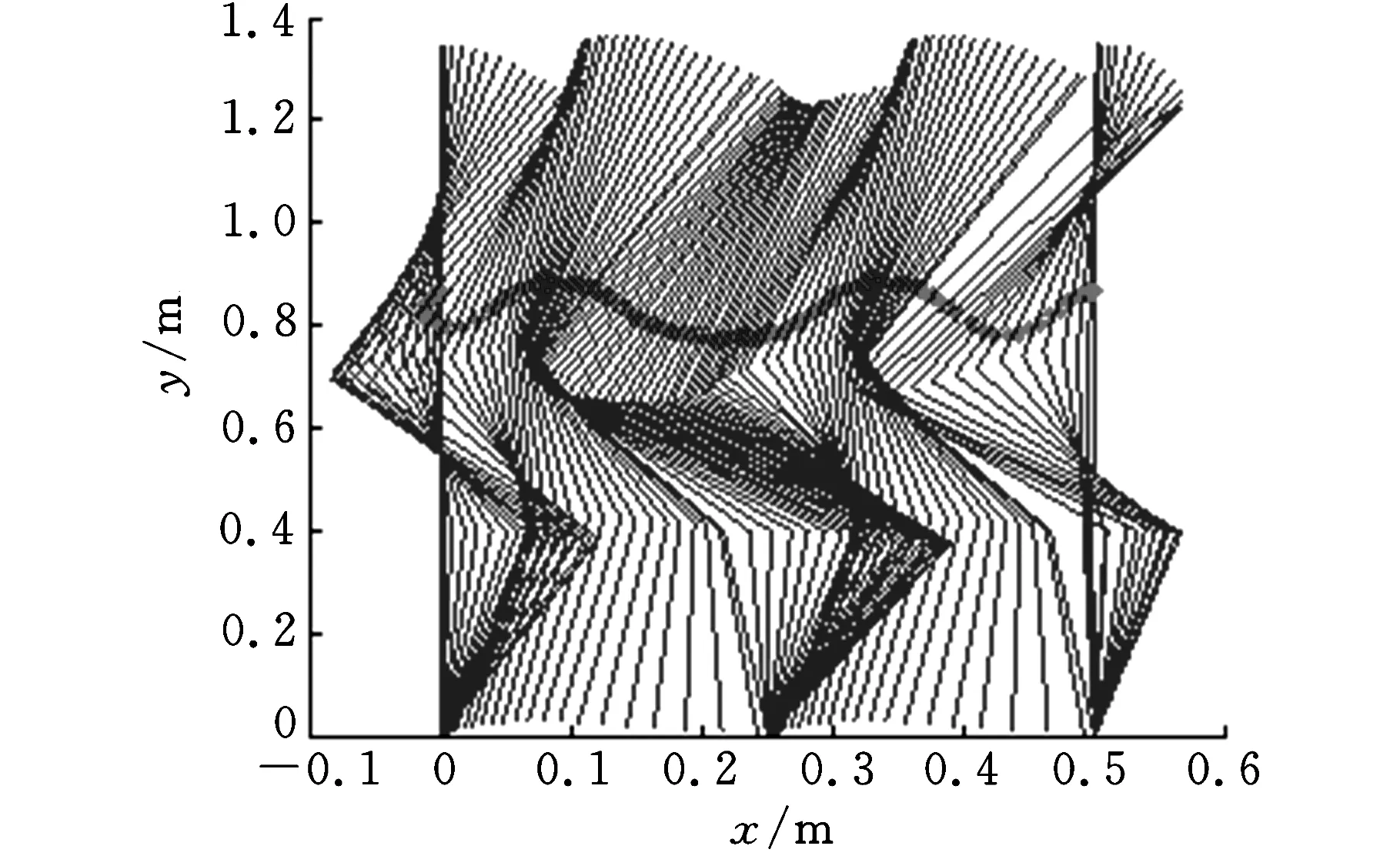
图15 水平地面上跳跃步态
机器人跳跃过程的棒状图如图15所示,依次包含开始段、腾空段、站立段、腾空段、停止段,图中一些点组成的一条从左至右的深色曲线表示质心轨迹。
3 结语
本文将单腿跳跃机器人的跳跃过程分为开始段、腾空段和站立段或停止段,采用参数化优化方法规划出了每个阶段的最优关节轨迹。与直接规划运动轨迹的方法相比,优化方法保证了运动过程中机器人关节控制势的最优;而参数化优化方法相对于非参数化优化方法大大减少了优化变量,提高了运算效率。以往关于轨迹规划的文献只是局限于在直接给定起跳状态和着地状态的情况实现轨迹的规划,既没有考虑机器人从静止状态能否达到需要起跳状态,也没有考虑机器人能否从给定的着地状态达到静止状态。本文则考虑了跳跃的全过程,采用参数化优化规划了机器人开始段和停止段的关节轨迹,实现了机器人从静止直立状态到起跳状态以及从碰地后状态到静止直立状态的过渡。
[1]郭小强,裴忠才. 跳跃机器人的研究现状与发展趋势[J]. 机械设计与制造,2011(11):173-175.
GuoXiaoqiang,PeiZhongcai.StudyStatusandDevelopingTreudofHoppingRobots[J].MachineryDesign&Manufacture,2011(11):173-175.
[2]ChenDiansheng,YinJunmao,HuangYu,etal.AHopping-rightingMechanismAnalysisandDesignoftheMobileRobot[J].JournaloftheBrazilianSocietyofMechanicalSciencesandEngineering,2013,4:469-478.
[3]詹望,葛文杰. 仿袋鼠跳跃机器人着地阶段的动力特性研究[J]. 机械设计,2007,24(6):23-25.
ZhanWang,GeWenjie.StudyontheDynamicPropertyintheTouchdownPhaseofKangarooSimulativeJumpingRobot[J].JournalofMachineDesign,2007,24(6):23-25.
[4]HyonSH,EmuraT,MitaT.Dynamics-basedControlofaOne-leggedHoppingRobot[J].ProceedingsoftheInstitutionofMechanicalEngineers.PartI:JournalofSystemsandControlEngineering,2003,2:83-98.
[5]CherouvimN,PapadopoulosE.ControlofHoppingSpeedandHeightOverUnknownRoughTerrainUsingaSingleActuator[C]//9thInternationalConferenceonRoboticsandAutomation.Kobe,Japan, 2009:2743-2748.
[6]VermeulenJ,LefeberD,VerrelstB.ControlofFootPlacement,ForwardVelocityandBodyOrientationofaOne-leggedHoppingRobot[J].Robotica,2003,1:45-57.
[7]UgurluB,KawamuraA.ZMP-basedOnlineJumpingPatternGenerationforaOne-LeggedRobot[J].TransactionsonIndustrialElectronics,2010,57: 1701-1709.
[8]VukobratovicM,BranislavB.ZeroMomentPoint:ThirtyFiveYearsofItsLife[J].InternationalJournalofHumanoidRobotics,2004,1:157-173.
[9]GuoQ,MacnabCJB,PieperJK.HoppingonEvenGroundandUpStairswithaSingleArticulatedLeg[J].JournalofIntelligentandRoboticSystems,2008,4:331-358.
[10]HasaneiniSJ,MacnabCJB,BertramJEA,etal.GlobalOptimumHuman-LikeGaitsforanArticulatedOne-LeggedHopper[C]//ASMEInternationalConferenceonAdvancedIntelligentMechatronics(AIM).Montréal,Canada,2010: 391-396.
[11]WuTingYing,YehTJ,HsuBing-Hung.TrajectoryPlanningofaOne-leggedRobotPerformingStableHop[C]//InternationalConferenceonIntelligentRobotsandSystems(IROS).Taipei,2010:4922-4927.
(编辑郭伟)
Trajectory Planning for an One-legged-hopper Robot
Wang ShenjiangGuo Zuhua
Beijing University of Aeronautics and Astronautics,Beijing,100191
An one-legged-hopper robot was simplified into a three-linkage model herein. The joints’ trajectory planning problem was studied during jumping motion. After summarizing the current trajectory planning methods of hopper robot, a parameteric optimization method was adopted in the research to minimize the control effort of robot joints. The jump motion was decomposed into four phases: starting phase, flight phase, stance phase and stopping phase. Joint trajectories of each segment were planned by optimization separately. Finally trajectories for all joints were obtained during the whole jumping motion that the robot moved from static stand upright state to next static stand state.
hopper robot; zero moment point(ZMP); optimization; trajectory planning
2014-11-17
TP242.6DOI:10.3969/j.issn.1004-132X.2015.17.010
王申江,男,1989年生。北京航空航天大学宇航学院硕士研究生。研究方向为仿人机器人。郭祖华,男,1971年生。北京航空航天大学宇航学院副教授。
