基于改进温度模型的300M钢本构方程参数识别
2015-10-29邢万强熊良山
邢万强 熊良山 汤 祁
华中科技大学,武汉,430074
基于改进温度模型的300M钢本构方程参数识别
邢万强熊良山汤祁
华中科技大学,武汉,430074
为了提高通过切削实验获取材料本构方程参数的精度,提出了将基于移动热源理论的温度分布模型沿剪切面积分计算剪切区平均温度的方法,结合不等距剪切区模型求得等效应变和应变率,建立了材料Johnson-Cook(J-C)本构方程参数的求解模型。根据切削实验获取的切削力和切屑厚度数据并采用遗传算法求得了300M钢J-C本构方程参数。与AdvantEdge FEM软件自带的300M钢本构模型相比,用所求模型参数仿真得到的主切削力、进给力和切屑厚度的精度有显著提高,验证了所建本构方程参数求解模型的有效性。
J-C参数识别;改进温度模型;300M钢;切削实验;有限元仿真
0 引言
300M超高强度钢(40CrNi2Si2MoVA)广泛应用于制造现代飞机起落架的外筒、活塞杆和轮轴等主要承力构件,是一种典型的航空难加工材料,其切削加工过程中的突出问题是刀具磨损严重、表面质量差以及加工效率低等,这会给起落架的安全性、可靠性以及生产成本带来严重影响[1]。随着计算机水平的发展,有限元仿真已成为研究切削加工的一种有效技术手段,而反映材料在切削条件下流变行为的材料本构方程参数的确定是进行切削过程精确仿真的基础和前提[2-6]。目前关于材料本构关系的研究主要集中在普通碳钢、铝合金、钛合金和高温合金上,对300M等超高强度钢动态本构关系的研究却鲜见报道。
传统的材料本构方程参数获取方法如霍普金森压杆实验(SHPB)法和泰勒杆实验法等存在拟合精度低、设备昂贵的缺点,因此,直接通过切削实验,结合切削分析模型(Oxley切削理论)计算变形区内的相关物理量,进而采用一定算法拟合求解出材料本构方程参数的方法,吸引了不少学者进行研究。基于切削实验的本构方程参数获取精度与剪切区等效应变、应变率和平均温度的计算精度直接相关,相关研究主要集中在对剪切区模型的改进上。例如,提出不等距剪切区模型[3],将剪应变率在剪切区的分布假设为分段线性[3]、分段多项式[4]或幂律分布[5]等。这些改进在一定程度上提高了剪切区等效应变和应变率的计算精度,但对剪切区温度计算模型的改进极其有限,在温度计算时仍普遍采用平均温度模型,如Oxley温度模型等[6],没有考虑剪切区温度计算对材料参数拟合结果的重要影响。研究表明,以移动热源理论为基础的分布式温度模型具有优于平均温度模型的精度[7],但尚未被应用于材料本构方程参数的求解模型。
本文将基于移动热源理论的分布式温度模型引入到材料本构方程参数求解的切削分析模型中,结合不等距剪切区模型,求解得到剪切区等效应变、应变率和平均温度,基于300M钢切削实验数据和遗传算法,优化得到300M钢的Johnson-Cook(J-C)方程参数,并通过将其应用于AdvantEdge FEM软件的正交切削仿真,验证了所提方法的正确性。
1 本构方程参数求解模型
1.1剪切区温度模型
Komanduri等[7]提出的温度模型是一种经典的以移动热源温度理论为基础的分布式温度模型,他们通过改变Hahn模型中的坐标系,并假设工件表面为绝热边界,引入镜像热源来计算倾斜带状移动热源在半无限空间内产生的温度,如图1所示。
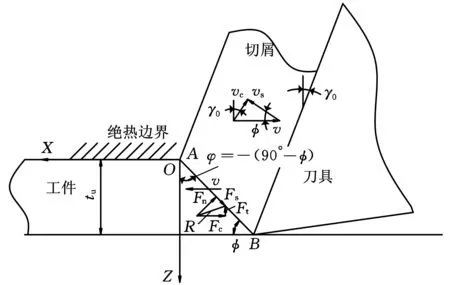
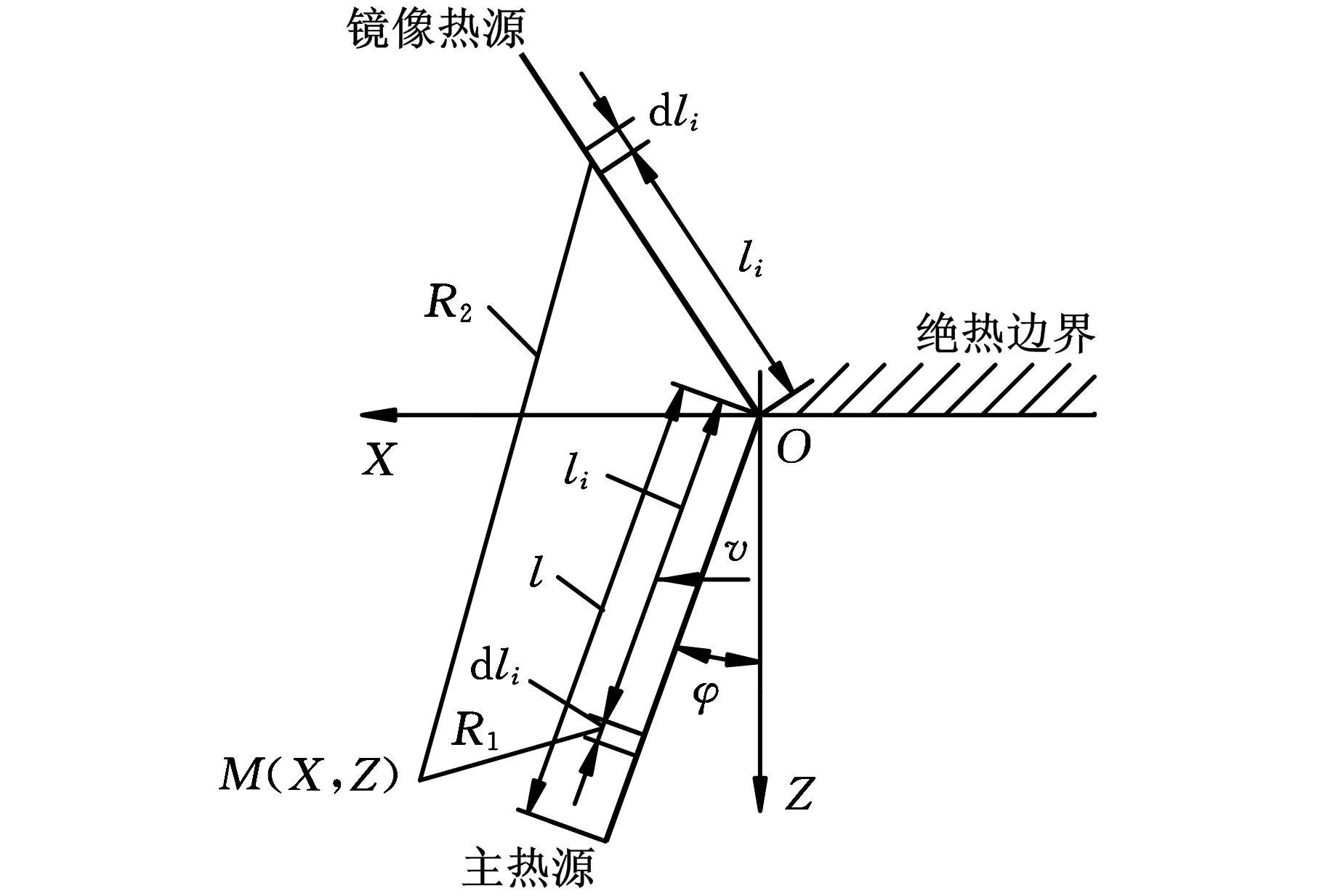
图1 倾斜带状热源在半无限大介质中移动的修正坐标系示意图
剪切区内任意一点M(X, Z)处由移动线热源引起的总温升可以看作是主热源和镜像热源综合作用的结果,由下式计算:
(1)

式中,φ为倾斜角,φ=-(90°-φ);φ为剪切角;K0为零阶第二类修正贝塞尔函数;a为热扩散率,定义a=λ/(ρ c);λ、ρ、c分别为热导率、密度和比热容;tu为未变形切屑厚度(相当于进给量f);tc为切屑厚度,由实验测得;γ0为刀具前角;qshear为主剪切区内由剪切变形产生的平均热流密度;Fs为剪切力,Fs=Fccosφ-Ffsinφ,Fc和Ff分别为主切削力和进给力(二者的值由切削实验测得); vs为切向速度;v为切削速度;lAB为剪切面长度,lAB=tu/sinφ;X、Z为剪切区内任意一点M的坐标;li为剪切线上一点到坐标原点的距离,见图1;w为切削宽度。
通过将式(1)中的温度分布TMshear(X,Z)沿主剪切面(长度为lAB)积分即可求得主剪切区的平均温度:
(2)
式中,T0为工件的初始温度;η为变形能转化为热量的比例(参考文献[8]取90%)。
值得注意的是,以往的研究通常将热导率λ和热扩散率a视为常数,但实际上它们是随温度变化的参数,因此本文采用迭代的方法计算剪切区平均温度TAB。例如,给定剪切区平均温度初始值TAB,可以求得该温度条件下的λ和a,根据λ和a又可以求得实际的平均温度TAB,如此迭代进行,直到连续两次求得的TAB充分接近为止。
主剪切区等效应变和应变率可以根据文献[4]中建立的不等距剪切区模型求得,相应计算公式如下:
(3)
(4)
未知变量C0是一个随材料和切削条件变化的参数,表示为剪切区厚度与长度的比值,该值可以通过文献[4]中的方法迭代求得。
1.2求解模型的建立
J-C本构方程形式简单,应用范围广,适用于描述大应变率下金属材料的应力应变关系,具体形式为
(5)

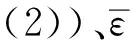
因此,建立式(6)所示的J-C方程参数求解的目标函数,采用一定的算法进行优化求解即可得到J-C方程中的5个参数:
(6)
式中,N为切削实验次数之和;i表示实验序号。
2 切削实验
测得多组切削条件下的主切削力、进给力和切屑厚度数据,代入上面建立的本构方程参数求解模型,即可得到300M钢在切削条件下的J-C本构方程参数。
2.1实验方案
实验所使用的工件材料是上海宝钢生产的300M超高强度钢棒料,毛坯加工后尺寸为φ125 mm×400 mm,材料经淬硬处理,硬度为HRC53,抗拉强度为1960 MPa,屈服强度为1630 MPa,延伸率δ为11.3%,断面收缩率ψ为46.9%。实验采用SANDVIK CBN刀具,刀片型号为CNGA120408S01030AWH 7025;刀杆型号为DCLNL 2525M 12,装夹后刀具主要几何参数为:刀尖圆弧半径rε=0.8 mm、前角γ0=-6°、后角α0=0°、主偏角Kr=95°、刃倾角λs=-6°。实验所用机床为配备了无级调速装置的CW6163E精密车床,机床最大加工长度为1500 mm,最大旋转直径为630 mm,额定功率15 kW。切削实验装置如图2所示。

图2 切削实验装置
为了使外圆车削尽可能地符合直角自由切削条件,在使刀具不发生过度磨损或崩刃的条件下尽量选取较大的切深,经多次试切,最终确定切深ap为1.5 mm(相当于求解模型中的切削宽度w)。从便于数据拟合和保证实验精度的角度分析,需要选择不同的切削速度和进给量进行实验,本文参考机床的实际工作条件和刀具推荐的切削用量选取4个水平的切削速度(50 m/min、100 m/min、150 m/min、200 m/min)和4个水平的进给量(0.15 mm/r、0.20 mm/r、0.26 mm/r、0.30 mm/r)。
2.2实验结果
实验方案如表1所示,采用Kistler三向测力仪(型号为Kistler9257A)测得每组切削参数下的主切削力和进给力。同时采集每组切削条件下的切屑,测量5个不同位置的厚度值,取其平均值作为该切削条件下切屑的厚度值。切削力和切屑厚度测量结果如表1所示。
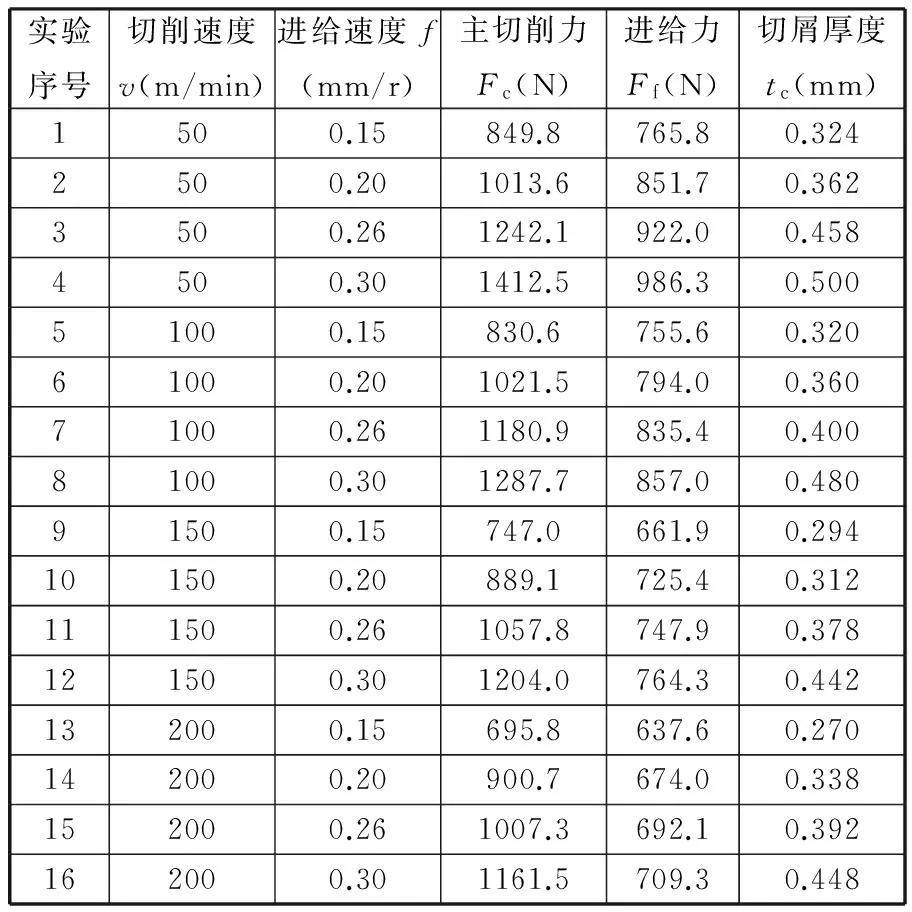
表1 实验设计表及实验结果
3 模型求解及验证
将本文建立的材料J-C参数求解模型编制为相应的MATLAB程序,通过输入表1中的切削参数和实验结果数据,采用遗传算法(GA)求解式(6)中建立的目标函数,其中求解模型中涉及到的相关材料热物理参数如表2所示。遗传算法的主要设置参数为:种群大小1000,精英数50,交叉率0.8,变异率0.1。

表2 300M钢的热物理性能[9]
J-C方程中5个待求参数的求解范围对保证得到精确合理的求解结果至关重要,以往文献中普遍采用的方法是将基于SHPB实验得到的J-C参数作为搜索的初始值,而公开的文献中无法查到300M钢的J-C参数,因此本文根据5个J-C参数的物理意义并参考其他钢材的J-C参数给出求解范围,各个参数的搜索范围及求解结果如表3所示。用于拟合J-C参数的温度范围为350~490 ℃、应变范围为0.82~1.51、应变率范围为6.9×103~1.2×105s-1。

表3 300M钢本构方程参数求解的搜索范围及结果
将本文所求的300M钢J-C参数以自定义材料模型的方式输入到有限元软件AdvantEdge FEM中进行二维切削过程仿真,将所得仿真结果与软件自带的300M钢材料模型的仿真结果以及实验结果进行比较。需要指出的是,当外圆车削中切削深度与进给量的比值较大时(本文切深为1.5 mm,进给量为0.15~0.3 mm/r),将外圆车削简化为二维切削仿真模型可以大大缩短仿真时间而不降低切削力等的仿真精度[10-12]。仿真中涉及到的相关材料热物理参数如表2所示,摩擦因数选用平均库仑摩擦因数,仿真所用的切削条件和刀具与实验相同。用以验证材料本构方程参数的实验数据从表1中以均匀交叉的方式选取,验证数据的实验序号1~8依次对应表1中的实验序号2、4、5、7、10、12、13、15。
图3给出了其中一组切削条件下自定义材料和软件自带材料得到的切屑形态仿真结果的比较,两种材料模型得到的切屑形态差别明显,前者切屑形态较宽且均匀,后者切屑较窄且扭曲变形严重,这与材料本构方程表达形式的不同有关,说明材料本构方程形式对切屑形态仿真结果的影响较大。
图4显示了自定义材料和软件自带材料模型的切削力和切屑厚度仿真结果与实验结果的比较,仿真模型中的主切削力和进给力分别指图3中X和Y方向的切削力。仿真结果的误差如表4所示。由图4和表4可知,与软件自带的材料本构模型相比,自定义本构模型的三个仿真结果均与实验值更为接近。另外,两种材料模型的仿真结果还表现出不同的规律。其中,自定义材料模型的主切削力仿真精度最高,而软件自带材料模型的主切削力仿真值与实验值相比普遍偏大;对于进给力,两种材料模型的仿真值均比实验值偏小,这是由于二维车削仿真没有考虑实际外圆车削中刀尖和副切削刃对已加工表面的摩擦挤压作用;对于切屑厚度,自定义材料模型的仿真值偏大而软件自带材料模型的仿真值偏小,与图3中显示的切屑形态一致。

(a)自定义材料模型
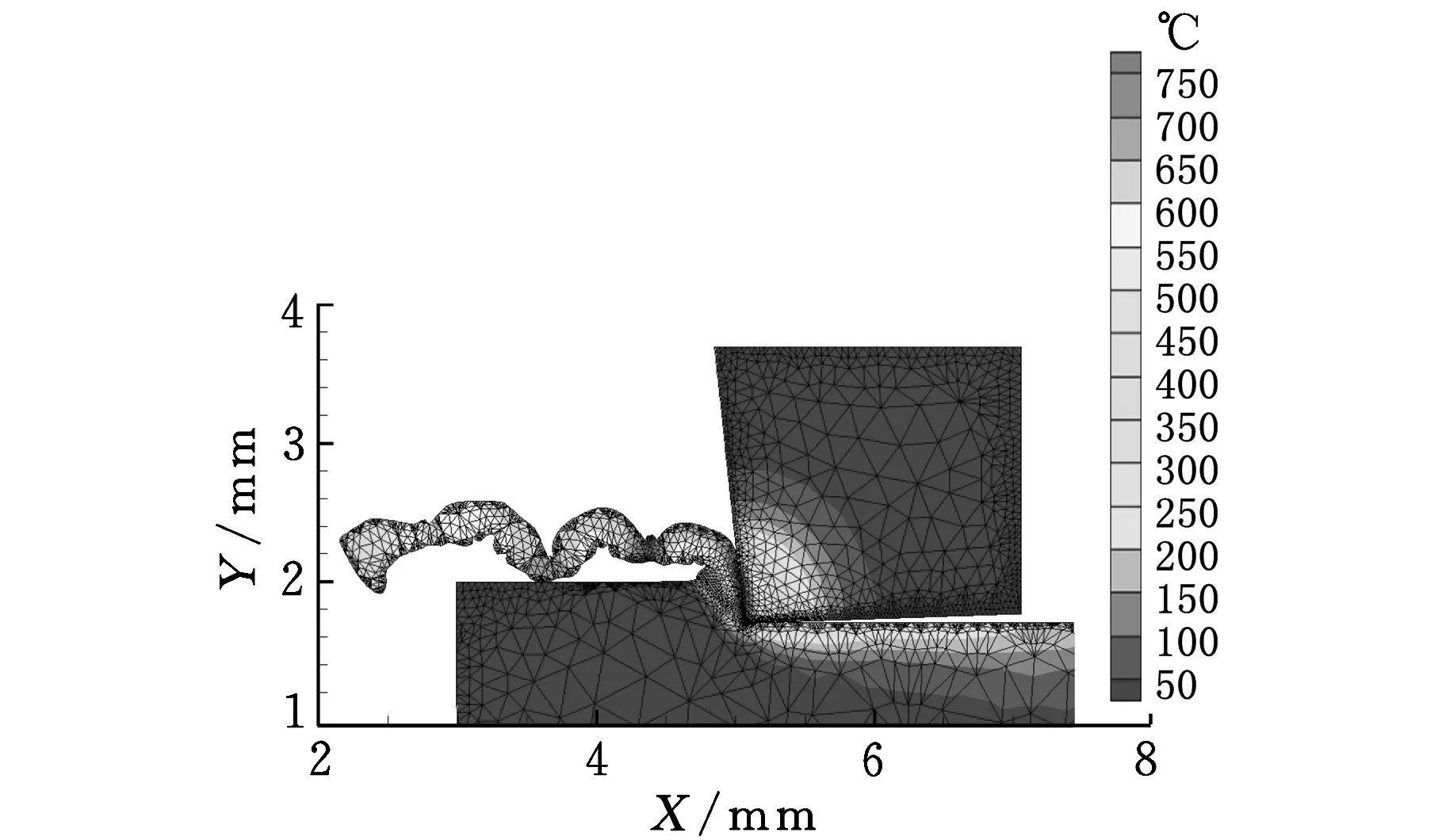
(b)软件自带材料模型图3 两种材料模型仿真得到的切屑形态(v=50 m/min,f=0.3 mm/r)
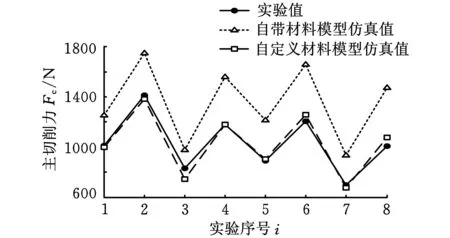
(a)主切削力

(b)进给力
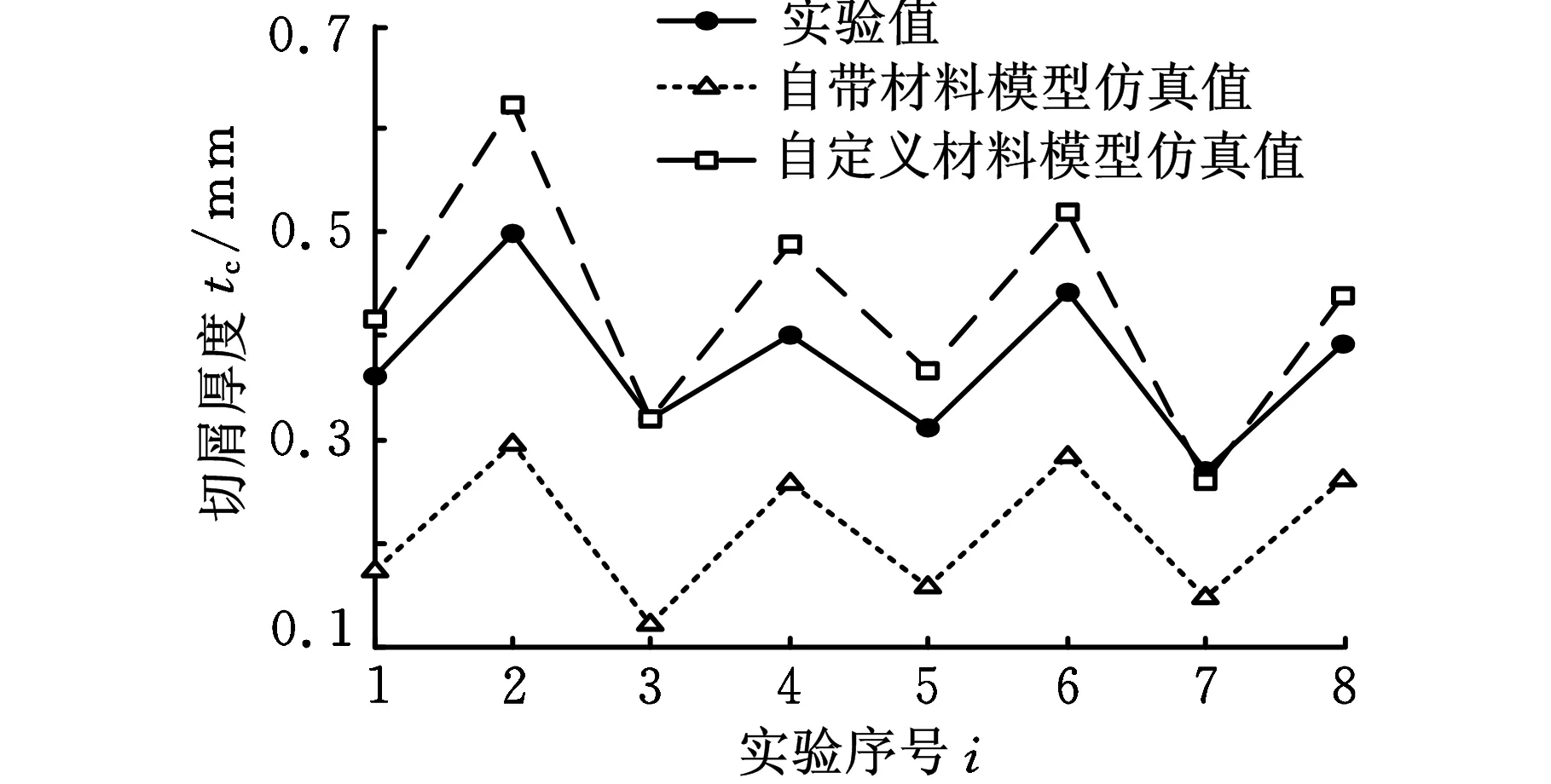
(c)切屑厚度图4 两种材料模型仿真结果与实验结果的比较
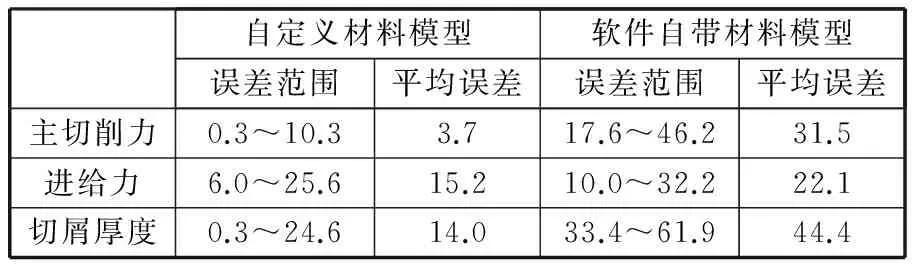
表4 两种材料模型仿真结果与实验结果的误差 %
总体而言,所求J-C模型的主切削力、进给力和切屑厚度仿真结果比软件自带材料模型的相应仿真结果更为精确,且相对实验结果的误差在可接受范围内,充分说明了本文所提方法是正确的、有效的。
4 结论
(1)所求J-C模型的主切削力、进给力和切屑厚度仿真结果相对实验结果的平均误差分别为3.7%、15.2%和14.0%,相比软件自带材料模型仿真结果的精度有显著提高,验证了所建本构方程参数求解模型的正确性和有效性。
(2)自定义材料模型和软件自带模型仿真得到的切屑形态差别明显,说明材料本构方程形式对切屑形态仿真结果影响较大。
(3)可以进一步将移动热源温度模型和不等距剪切区模型结合起来作为Oxley切削理论的改进模型,以提高对切削过程的解析预测精度。
[1]张慧萍,王崇勋,杜煦. 飞机起落架用300M超高强度钢发展及研究现状[J]. 哈尔滨理工大学学报,2011,16(6):73-76.
Zhang Huiping,Wang Chongxun,Du Xu. Aircraft Landing Gear with the Development of 300M Ultra High Strength Steel and Research[J]. Journal of Harbin University of Science and Technology,2011,16(6):73-76.
[2]凌玲,李星星,王学林,等. 0Cr18Ni9不锈钢本构模型及其对切削力预测影响分析[J]. 中国机械工程,2012,23(18):2243-2248.
Ling Ling,Li Xingxing,Wang Xuelin,et al. Constitutive Model of Stainless Steel 0Cr18Ni9 and Its Influence on Cutting Force Prediction[J]. China Mechanical Engineering,2012,23(18):2243-2248.
[3]Tounsi N,Vincenti J,Otho A,et al. From the Basics of Orthogonal Metal Cutting toward the Identification of the Constitutive Equation[J]. International Journal of Machine Tools and Manufacture,2002,42(12): 1373-1383.
[4]Pang L,Kishawy H A. Modified Primary Shear Zone Analysis for Identification of Material Mechanical Behavior during Machining Process Using Genetic Algorithm[J]. Journal of Manufacturing Science and Engineering,2012,134(4):041003.
[5]Li Binglin,Wang Xuelin,Hu Yujin,et al. Analytical Prediction of Cutting Forces in Orthogonal Cutting Using Unequal Division Shear-zone Model[J]. International Journal of Advanced Manufacturing Technology,2011,54(5/8):431-443.[6]Özel T,Zeren E. A Methodology to Determine Work Material Flow Stress and Tool-chip Interfacial Friction Properties by Using Analysis of Machining[J]. Journal of Manufacturing Science and Engineering,2006,128(1): 119-129.[7]Komanduri R,Hou Z B. Thermal Modeling of the Metal Cutting Process: Part I—Temperature Rise Distribution Due to Shear Plane Heat Source[J]. International Journal of Mechanical Sciences,2000,42(9):1715-1752.[8]Lalwani D I,Mehta N K,Jain P K. Extension of Oxley’s Predictive Machining Theory for Johnson and Cook Flow Stress Model[J]. Journal of Materials Processing Technology,2009,209(12): 5305-5312.[9]《中国航空材料手册》编辑委员会. 中国航空材料手册. 第1卷结构钢、不锈钢[M]. 2版. 北京:中国标准出版社,2001.
[10]严宏志,龚黎军. 20CrMo材料本构模型及其有限元模拟[J]. 中南大学学报(自然科学版),2012,43(11): 4268-4273.
Yan Hongzhi,Gong Lijun. Constitutive Model and Finite Element Simulation of 20CrMo Material[J]. Journal of Central South University (Science and Technology),2012,43(11):4268-4273.
[11]理俊杰,轧刚,王时英,等. AZ31B镁合金的本构方程建立及切削性能分析[J]. 工具技术,2012,46(4): 25-27.
Li Junjie,Ya Gang,Wang Shiying,et al. Constitutive Equation Establishment and Cutting Characteristics Analysis of AZ31B Magnesium Alloy[J]. Tool Engineering,2012,46(4):25-27.
[12]付杰. 难加工金属材料切削加工过程物理仿真与试验研究[D]. 长沙:湖南大学,2013.
(编辑苏卫国)
Identification of Constitutive Equation Parameters of 300M Steel Based on Improved Temperature Model
Xing WanqiangXiong LiangshanTang Qi
Huazhong University of Science and Technology,Wuhan,430074
In order to improve the accuracy of material constitutive equation parameters obtained from cutting experiments, a method to calculate average temperature in primary shear zone was proposed by integrating the temperature distribution equitation based on the moving heat source theory along the shear plane length, combining with the equivalent strain and strain rate calculated from the unequal divided shear zone model. A solution model for material Johnson-Cook(J-C) constitutive equation parameters was established. Through the cutting force and chip thickness data obtained from cutting experiments and genetic algorithm, the parameters in J-C constitutive equation of 300M steel were identified. Compared with the default constitutive model of 300M steel in AdvantEdge FEM software, the accuracy of main cutting forces, thrust forces and chip thicknesses simulated by the new obtained J-C model parameters is improved significantly, which demonstrates the effectiveness of the proposed solution model for constitutive equation parameters.
identification of J-C parameters; improved temperature model; 300M steel; cutting experiment; FEM simulation
2014-05-21
国家重点基础研究发展计划(973计划)资助项目(2011CB706803);国家科技支撑计划资助项目(2012BAF08B01)
TH142;TG506DOI:10.3969/j.issn.1004-132X.2015.17.004
邢万强,男,1989年生。华中科技大学机械科学与工程学院硕士研究生。主要研究方向为切削过程建模、刀具设计优化。发表论文2篇。熊良山,男,1965年生。华中科技大学机械科学与工程学院副教授。汤祁,男,1990年生。华中科技大学机械科学与工程学院硕士研究生。
