空间非圆齿轮双侧同步驱动板坯结晶器非正弦振动的研究
2015-10-29刘大伟任廷志
刘大伟 任廷志 金 昕
1. 燕山大学,秦皇岛,0660042.燕山大学国家冷轧板带装备及工艺工程技术研究中心,秦皇岛,066004
空间非圆齿轮双侧同步驱动板坯结晶器非正弦振动的研究
刘大伟1任廷志2金昕2
1. 燕山大学,秦皇岛,0660042.燕山大学国家冷轧板带装备及工艺工程技术研究中心,秦皇岛,066004
针对液压式板坯结晶器驱动系统投资高昂、控制复杂、双缸同步性差等问题,提出了由空间非圆齿轮组成的两点连接、同步输出的板坯结晶器非正弦驱动系统。以新型空间非圆齿轮副为变速比传动机构,与偏心轴连杆一起合成结晶器的非正弦振动速度;建立了给定传动比下,波状面齿轮副的节曲线封闭条件和数学模型,并以此为基础,构建出振动波形具有匀速段特征的空间非圆齿轮节曲线;最后通过仿真计算,说明了根据给定非正弦波形设计非正弦驱动系统的流程。与其他形式的非正弦驱动系统相比,该系统不需伺服控制,且同步性能好,成本低,具有推广价值。
板坯结晶器;非正弦振动;空间非圆齿轮;同步性能
0 引言
在连续铸钢生产中,连铸机的结晶器必须按一定规律进行振动,以保证铸坯与结晶器的润滑条件,防止结晶器与新生坯壳之间发生黏结。随着人们对铸坯与结晶器间各种复杂物理机理认识的深入,结晶器振动波形一直发生着变化,其中非正弦波形被公认为是目前实现高效连铸的最优波形,因此开发运行可靠、波形稳定、维护方便的先进非正弦驱动装备成为国内外工程界的热点问题,也是各大冶金企业关注的焦点。
当前的非正弦驱动装备根据传动原理可分为液压式和电动式两大类。液压式驱动系统可以方便地产生各种振动规律,实现在线参数调整[1],但其建造、运行及维护成本高昂,另外液压缸存在偷停现象,液压油易造成环境污染。相比较而言,电动式驱动系统投资成本较低,设备维护方便,无污染,大有取代液压式驱动系统的趋势。电动式驱动系统主要有四种:镭目公司[2]采用伺服电动缸直接驱动结晶器非正弦振动,可实现振幅、频率和波形的在线调整,但伺服电机频繁正反转动影响控制精度,其核心传动构件滚柱丝杠的承载和抗冲击能力难以与液压缸或曲柄机构相媲美;Yao等[3]提出伺服电机、减速器和偏心轴连杆机构组成的驱动系统,此时伺服电机单向变速转动,波形和频率在线可调,振幅停机可调;直驱电机与偏心轴连杆机构组成的驱动系统在结构上最为简单,但驱动功率有限,振幅同样无法在线调整[4];为了降低控制系统的成本和难度,采用变频电机、非匀速传动机构和偏心轴连杆机构的组合型式也非常实用,其操作维护方便,投资及运行费用低,可靠性高,并且对原有的机械式正弦振动机构改造方便[5-6]。
由于结构、功率和同步控制等原因,上述四种电动驱动方式主要应用于小方坯连铸机上,大型板坯连铸机的非正弦驱动系统几乎全部为双缸液压式,但是其双缸同步性较差并伴有突然停振、零飘、颤振等缺陷。因此在吸收各种驱动方式的特点后,综合考虑使用效果和经济效益等因素,提出由变频电机、新型空间非圆齿轮和偏心机构组成的大型板坯结晶器驱动系统,不仅可以在振动台双侧同步实现精确非正弦波形,而且设备运行可靠、成本最低。
1 空间非圆齿轮双侧同步驱动系统的结构原理
板坯连铸机结晶器的振动系统一般由驱动系统、板簧导向机构、缓冲装置和振动台组成。生产时,结晶器与振动台固接,驱动系统与振动台相连,然后通过导向机构和缓冲装置的综合作用,实现以合理的功率驱动结晶器按特定轨迹运动的目的。
目前驱动系统与振动台有两种连接方式:两点连接和四点连接[7]。液压式采用两点连接,两个液压缸分布在振动台两侧,振动台的运动轨迹由导向板簧控制,液压缸只起振动发生作用;四点连接是指驱动系统与振动台四角相连,这时驱动系统除了起振源的作用,还可以通过控制四角的振幅使振动台做直线或仿弧运动,它与板簧机构共同作用,控制振动台的运动轨迹,电动式驱动系统往往采用该结构。比较两种连接方式可知,两点连接中驱动系统的功能唯一,且振动发生单元少,其同步控制难度相对较低,另外结晶器轨迹完全由板簧控制,具有工作可靠、寿命长、精度高和免维修等优点。因此借鉴液压驱动中两点连接方式,提出了一种新型的电动式非正弦驱动系统,其结构如图1所示。
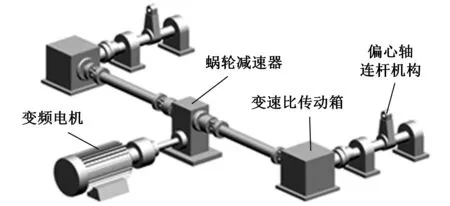
图1 双侧同步驱动系统简图
该驱动系统中变频电机与双输出轴蜗轮减速器的输入轴连接,蜗轮减速器的两个输出轴通过万向联轴器与回转轴线正交的两个变速比传动箱相连,在两个变速比传动箱的输出轴上安装相位角完全相同的两个偏心轴连杆机构,最后连杆机构的输出端与振动台铰接。当电机匀速转动时,通过变速比传动箱与偏心轴连杆机构的速度合成,实现振动台的非正弦振动,因此变速比传动箱是整个系统的核心。
2 核心传动部件的设计
文献[6]提出了由平面非圆齿轮组成的方坯结晶器非正弦驱动方案,若要将平面非圆齿轮应用于图1所示的双侧驱动系统,那么在变速比传动箱中平面非圆齿轮要与圆锥齿轮组合使用,才能实现正交轴间的变速比传动,这无疑将增加系统的复杂程度,降低系统的精度。因此在变速比传动箱中,选用能够实现正交轴间变速比传动的空间非圆齿轮,可以用最少的传动零件实现双驱动系统的非正弦振动,是该系统的最佳设计方案。
非圆锥齿轮副[8]和直齿非圆齿轮与特殊面齿轮组成的齿轮副[9]是现有的两种空间非圆齿轮副,为了便于描述,将第二种空间非圆齿轮副称为波状面齿轮副。波状面齿轮副与非圆锥齿轮副相比,具有装配精度要求不高,直齿非圆齿轮无轴向力,振动和噪声低等优点,故选用波状面齿轮作为双驱动系统的核心传动部件。波状面齿轮副是一种新型的空间非圆齿轮副,但文献[9]仅讨论了直齿椭圆齿轮及其共轭面齿轮的特殊传动形式,而更多场合下是要根据实际的传动比设计专用的非圆齿轮,因此必须完善波状面齿轮副的节曲线设计理论。
2.1波状面齿轮副节曲线封闭条件
波状面齿轮副由一个直齿平面非圆齿轮和与其共轭的特殊面齿轮组成,二者的回转轴线正交,节曲线如图2所示。平面非圆齿轮绕轴O2A旋转,节曲线为一条平面非圆曲线,点O2与其在同一平面内,波状面齿轮绕轴O1A旋转,节曲线为一条绕在圆柱体上的空间曲线,点O1在圆柱体底部端面上。

图2 波状面齿轮副空间节曲线简图
当波状面齿轮副传动时,二者的节曲线发生纯滚动,在滚动接触点B处,非圆齿轮的回转半径为其节曲线在B点处的向径r,而波状面齿轮的回转半径为圆柱体的半径R,则波状面齿轮副传动比为
(1)
式中,φ1和φ2分别为波状面齿轮和平面非圆齿轮的转角,rad;w1和w2分别为波状面齿轮和平面非圆齿轮的转速,rad/s;t为时间,s。
r随平面非圆齿轮的转角φ2变化,R为固定值,所以当两个齿轮转动时,能够实现变速比传动规律。根据式(1)可得波状面齿轮的转角表达式:
(2)
为了实现稳定连续的传动,二者的节曲线必须保证是光滑且封闭的,若平面非圆齿轮的节曲线是光滑的,那么与之共轭的波状面齿轮节曲线也应该是光滑的,所以r(φ2)的一阶导数是连续的。若要保证二者节曲线是封闭的,则应满足:
(3)
式中,n1和n2分别为波状面齿轮和平面非圆齿轮节曲线的周期数。
比较式(3)与平面非圆齿轮副节曲线封闭公式可知:凡是满足平面非圆齿轮节曲线封闭条件的传动比函数,都可以构建出封闭的波状面齿轮副节曲线,该性质同样适用于非圆锥齿轮,这就统一了平面和空间非圆齿轮副的连续传动条件。
2.2波状面齿轮副节曲线方程
图2中,坐标系O1x1y1z1与O2x2y2z2分别固定在平面非圆齿轮与波状面齿轮上,其中轴x1与波状面齿轮的回转轴线O1A重合,轴z2与平面非圆齿轮的回转轴线O2A重合。在两个齿轮传动的初始位置,如图2中所示,轴x1与轴x2,轴y1与轴y2以及轴z1与轴z2互相平行。若已知给定传动比i12,则平面非圆齿轮节曲线的极坐标方程根据式(1)可以得到r(φ2)=Ri12(φ2),将其转化到直角坐标系O2x2y2z2中为
(4)
将平面非圆齿轮与波状面齿轮节曲线在滚动过程中的重合点坐标从O2x2y2z2转化到O1x1y1z1后,即可得到波状面齿轮的节曲线方程:
(5)
式中,a为线段O1A的长度,mm。
在给定传动比i12后,将i12代入式(4),然后设计出参数R,即可得到波状面齿轮副的节曲线方程,选取R时应满足平面非圆齿轮上有整数个轮齿,即
(6)
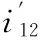
2.3双驱动系统非正弦波形及相应波状面齿轮副
波状面齿轮副中的平面非圆齿轮作为从动轮与图1中的偏心轴连杆机构相连,为了便于表示系统的机构简图,将波状面齿轮用平面非圆齿轮代替,如图3所示。偏心轴连杆机构简化成曲柄滑块机构,其中滑块代表结晶器振动台,曲柄与从动轮2固定连接。φ2为从动轮节曲线的极角,与转角方向相反,但大小相等,二者可互相替代。
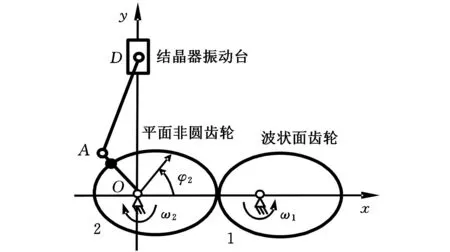
图3 驱动机构平面简图
构建具有匀速段特征的非正弦波形如图4所示,令图3中的平面非圆齿轮转角φ2∈(0,β]时,结晶器向上匀速运动,且匀速运动的区间正好在结晶器向上运动过程的中间。结晶器的振幅h与曲柄OA的长度相等,一般为3~5mm,h相对连杆AD的长度很小,结晶器振动台的位移可表示为
(7)
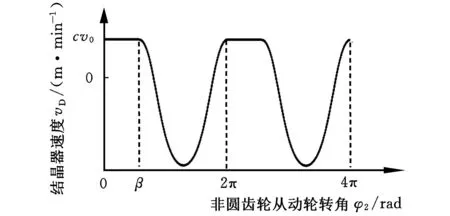
图4 非正弦振动波形
对式(7)求时间的导数可得结晶器的速度公式:
(8)
式中,f1为结晶器的频率,min-1。
匀速段的速度为结晶器向上运动的最大速度vmax=cv0=cπf1h/1000,令vD=vmax,将其代入式(8),可得结晶器在匀速段时波状面齿轮的传动比:
(9)
式中,c代表非正弦振动的最大速度vmax与相同振幅和频率下正弦振动最大速度v0的比值。
(10)

求解式(10)可以得到传动比i2中的系数,然后代入式(8)得到结晶器的非正弦速度波形:
(11)
一般使用的非正弦波形是关于时间的函数,在式(11)的基础上,进一步推导,得到由分段参数方程表示的波形,其中匀速段方程为
(12)
0<φ2≤β
式中,t1和vD1分别为匀速段结晶器运动时间(s)和速度(m/min)。
非匀速段方程为
(13)
β<φ2≤2π
式中,t2和vD2分别为非匀速段结晶器运动时间(s)和速度(m/min)。
图2中非正弦波形的两段速度曲线圆滑过渡,其加速度曲线保持连续,则设备运行无冲击。该波形具有匀速段特征,能够最大限度地降低结晶器的最大正速度,减小铸坯与结晶器之间的摩擦力,另外参数c和β可分别独立控制结晶器的最大正速度和负滑动时间,在设计波形时,能够更加充分地发挥出非正弦振动工艺的优势[6]。
最后将i1和i2的公式代入式(4)和式(5)中,即可得到波状面齿轮副的节曲线,其中平面非圆齿轮可由数控插齿机加工,而波状面齿轮可先根据齿廓数学模型计算出齿面数据,然后用数控铣床进行加工。
3 仿真实例
设计结晶器双侧驱动系统的关键问题在于波形参数的确定及在此基础上核心传动部件的几何参数设计。波形参数目前没有统一的确定方法,因此调研了多条国产和进口的板坯连铸机的振动参数及相应的产品表面质量,并对其工艺参数进行详细计算和比较后,得到了一组非正弦波形参数,有助于减轻铸坯表面振痕深度,并且加强润滑效果,减少铸坯拉漏事故。波形公式(式(12)、式(13))中的设计参数为:c=0.65,β=0.8rad,h=3.5mm,频率f1根据铸坯拉速可以调整,当f1=180min-1时,结晶器的速度曲线如图5所示,为了与常用波形的表达方式统一,其横坐标以时间t为变量。
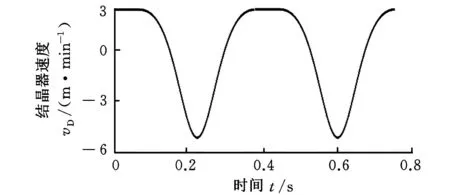
图5 结晶器非正弦速度曲线
根据给定参数c与β设计的一对波状面齿轮副如图6所示,图6a为波状面齿轮三维模型图,图6b为齿轮副的装配图。

(a)波状面齿轮三维模型(b)齿轮副的装配图图6 波状面齿轮副三维模型
波状面齿轮作为图1中变速比传动箱的主动轮,平面非圆齿轮作为从动轮,当变频电机的转动频率为180 min-1,那么该驱动系统的两个连杆可以同步驱动结晶器两侧,实现图3中的非正弦波形。
4 结论
(1)与双缸液压式驱动系统相比,在由空间非圆齿轮组成的双侧驱动系统中,偏心轴连杆机构共用同一个原动机,可非常容易地实现同步运动,并且系统不需复杂的伺服控制,即可得到准确的非正弦振动波形。
(2)新型驱动系统成本保守估计仅为液压式的1/8左右,其后续运行和维护的二次成本相对液压式更低,因此该驱动系统非常适合目前钢铁行业急需淘汰落后产能,降低生产成本的大环境。
(3) 完善了波状面齿轮副节曲线理论,可应用于根据给定传动比设计正交轴空间非圆齿轮的场合。
[1]李常青,孙丽娟,袁清鸿,等. 板坯结晶器液压振动装置:中国,200810048798.1[P],2008-08-13.
[2]田志恒,田立,周永,等. 结晶器非正弦振动系统的开发与应用[J]. 钢铁,2004,39(增刊):623-629.
Tian Zhiheng, Tian Li,Zhou Yong,et al. Development and Application of Non-sinusoidal Oscillation System[J]. Iron and Steel,2004,39(S):623-629.
[3]Yao Yunfeng, Li Xiankui, Fang, Yiming, Zhang Liping. Study of Non-sinusoidal Oscillation of Continuous Casting Mold Driven by Servomotor[J]. Journal of Iron and Steel Research International, 2008, 15(1): 558-562.
[4]曹铁军,王鹏,刘奎奎. 直接驱动结晶器振动发生装置及其振动方法:中国,200910057435.9[P],2009-06-17.
[5]张立平,李宪奎,杨红普,等. 逆平行四连杆机构的非正弦波及工艺参数[J]. 机械工程学报,2009,45(5):301-036.
Zhang Liping,Li Xiankui,Yang Hongpu,et al. Non-sinusoidal Wave and Process Parameters of Anti-parallel Four-bar Linkage[J]. Journal of Mechanical Engineering,2009,45(5):301-036.
[6]刘大伟,任廷志. 非圆齿轮驱动结晶器非正弦振动的研究[J]. 中国机械工程,2013,24(3):327-330.
Liu Dawei,Ren Tingzhi. Research on Non-sinusoidal Oscillation of Mold Driven by Noncircular Gears[J]. China Mechanical Engineering,2013,24(3):327-330.
[7]蔡开科. 连铸结晶器[M]. 1版. 北京:冶金工业出版社,2008.
[8]贾巨民,高波,索文莉,等. 越野汽车新型变速比差速器的研究[J]. 中国机械工程,2012,23(23):2844-2847.
Jia Jumin,Gao Bo,Suo Wenli,et al. Study on a New Type of Differential with Variable Ratio for Off-road Vehicles[J]. China Mechanical Engineering,2012,23(23):2844-2847.
[9]Lin Chao,Gong Hai,Nie Gang,et al. Geometry Design,Three-dimensional Modeling and Kinematic Analysis of Orthogonal Fluctuating Gear Ratio Face Gear Drive[J]. Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science,2013,227(4):779-773.
(编辑郭伟)
Research on Non-sinusoidal Oscillation of Slab Mold Driven by Two Spatial Noncircular Gear Sets Synchronously
Liu Dawei1Ren Tingzhi2Jin Xin2
1.Yanshan University,Qinhuangdao,Hebei,066004 2.National Engineering Technology Research Center of Cold Rolling Strip Equipment and Technology,Yanshan University,Qinghuagndao,Hebei,066004
Due to the disadvantages of the vast investment, complicated control and weak synchronization of hydraulic driven device of slab molds, a new non-sinusoidal system comprised of spatial noncircular gears was presented with two point joint and synchronous output. Its transmission principle was given that the non-sinusoidal oscillation velocity of molds was composited by that of a pair of spatial noncircular gears and the eccentric shaft mechanism. The closed conditions and the mathematical model of pitch curves of the undulating face gear set were built under given transmission ratio, with non-sinusoidal wave constructed. Finally, the process for designing non-sinusoidal driven system under given wave function was illustrated through simulations. With the advantages of good synchronism and low cost over other driving styles, the new system has wide promotional values.
slab mold;non-sinusoidal vibration;spatial noncircular gear;synchronism
2014-11-20
河北省自然科学基金钢铁联合研究基金资助项目(E2011203078);燕山大学青年教师自主研究计划项目(14LGB003)
TH132DOI:10.3969/j.issn.1004-132X.2015.17.009
刘大伟,男,1984年生。燕山大学机械工程学院讲师、博士。研究方向为冶金机械设计。任廷志,男,1960年生。燕山大学国家冷轧板带装备及工艺工程技术研究中心教授、博士。金昕(通信作者),男,1975年生。燕山大学国家冷轧板带装备及工艺工程技术研究中心副教授、博士。
