曲线间中心线的自动创建方法
2023-01-10戈家荣王占宇陈丽岩段晓松
戈家荣,王占宇,陈丽岩,段晓松
(1.绍兴宝旌复合材料有限公司,浙江 绍兴 312073;2.精功(绍兴)复合材料技术研发有限公司,浙江 绍兴 312073)
0 引言
曲线间的中心线是到两条曲线距离相等点的轨迹,又称为中线、中间线或中轴线,广泛应用于机械制图、道路设计、地图绘制等领域。
中心线的定义最早由BLUM H[1]于1967年提出,原理为草地燃烧模型。假设草地的边界为两条曲线,两条边界同时点燃并沿内部方向等速燃烧,随着燃烧面积的扩大,两个火源相交点的轨迹即形成中心线。
基于草地燃烧原理,CAO L X等[2]提出了一种利用偏置曲线生成中心线的方法,如图1所示。大圆和小圆沿相对方向,以步长λ依次偏置曲线,并计算每对偏置曲线的交点,将所有交点连接起来即形成中心线。但是当两条曲线的距离不是线性变化时,可能存在多个点与两曲线的距离值相等,即一对偏置曲线存在多个交点,导致最后生成多个无序点的集合。故需要对这些点重新排序后才能生成中心线。这增加了不少额外的工作量,也可能影响中心线的准确性。
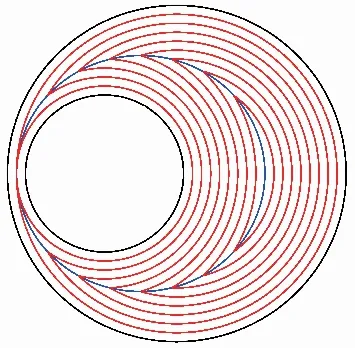
图1 偏置曲线法
董箭、刘秀芳等[3-4]提出了一种基于缓冲区边界相向逼近求交模型的曲线间中心线生成算法。如图2所示,Dmax、Dmin分别代表曲线L1、L2之间的最大和最小距离,两条曲线在缓冲距离从Dmax至Dmin/2区间,以步长λ逐步生成缓冲区,并依次计算两个缓冲区边界的交点,连接所有交点即形成中心线。该方法存在与上述CAO L X等所提方法类似的缺点,需要对产生的无序点进行后处理。

图2 缓冲区法
CAO L X、GHATREHNABY M等[5]、DORADO R[6]提出了一种利用内切圆生成中心线的方法,如图3所示。对于曲率线性变化的曲线,该方法不仅计算速度快,且生成的中心线精度很高,曲线也很光顺,但对于一些曲率非线性变化的曲线,由于内切圆是沿曲线按给定的步长λ移动的,内切圆半径与曲线曲率有很大关系,导致内切圆半径非线性变化,使形成中心线L的轨迹点分布不均匀,直接影响中心线的精度,在端部还容易生成异常内切圆,使中心线L产生畸变,需要人工辅助识别和处理,一定程度上降低了该方法的效率和准确性,如图4所示。

图3 内切圆法

图4 内切圆法生成的错误结果
乔庆华、张立锋等[7-8]提出了一种利用Delaunay三角网格创建中心线的方法,如图5所示。该方法的原理是将目标区域离散为Delaunay三角网格,通过提取这些网格的外心或内心,并将这些点连成中心线。该方法生成的中心线并不严格符合曲线间中心线的数学定义,只是一个近似算法,结果可能与理论值相差较大。

图5 Delaunay三角网格法
杨得志等[9]提出了一种基于矢量方法的中心线生成算法——单位圆滚动追踪法,如图6所示。该方法的原理为:连接曲线L1的起点P11和曲线L2的起点P21,并创建其中点PS,从PS沿曲线反方向作垂线并获得与PS距离为R的点A。设置点A为搜索起点,以点A为圆心、半径为R作单位圆,该单位圆上必然存在一点P1与两条曲线距离相等,并用牛顿迭代法查找到该点。再以点P1为圆心、半径为R作单位圆,则该单位圆上必然存在一点P2与两条曲线距离相等,以此类推获得其他等距点Pi,直到点Pi与终点PE的距离小于单位圆半径R时停止,连接所有等距点即形成中心线L。该方法运算速度快,生成的中心线比较光顺,精度与单位圆半径R和等距判定阈值有关。但单位圆半径R比较难确定,R过大容易导致等距点分布太细,影响中心线精度;R过小则会导致运算速度降低,甚至找不到等距点,如图7所示。
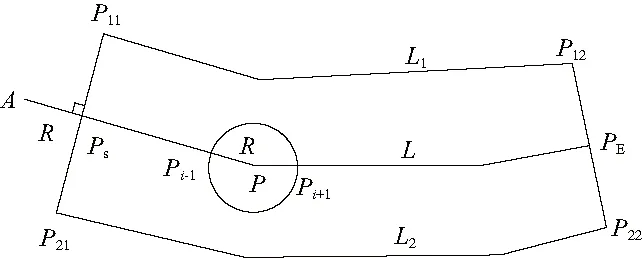
图6 单位圆滚动法

图7 单位圆滚动法生成的异常结果
为此,本文提出一种自动创建曲线间中心线的新方法。该方法基于等距原则和有限元法,编制程序自动创建曲线间的中心线,且中心线的精度可按需调整,并以两条曲率非线性变化的自由曲线和某复合材料导弹弹翼为例,验证了所提方法的可行性和有效性。
1 设计原理
1.1 等距法
中心线上所有点与两条曲线的距离应相等,或小于等距判定的阈值δ。机械设计行业一般要求δ≤0.02 mm,即一般数控机床的加工精度,这样才能保证制造出的产品满足设计要求。
1.2 有限元法
两条曲线上分别按给定步长λ创建n个等分点,等分点的数量可按实际确定,要求中心线的误差≤0.02 mm,一般λ≤10 mm。将两条曲线上的等分点逐对连起来,并在该直线上创建中点。
1.3 二分法
通过不断修改点在直线上的比例参数,使该点与两条曲线的距离相等或小于阈值δ,则该点为等距点。如图8所示,连接曲线L1的起点P11和曲线L2的起点P21,并作其中点P1,则点P1在直线P11P21上的初始比例Ri为0.5。设比例下限RL=0(表示该点在曲线L1上),比例上限RU=1(表示该点在曲线L2上),点P1到曲线L1、L2的距离分别为D1、D2。首先进行第1次迭代计算,如果D1>D2,则表示比例参数在0~0.5之间,使用二分法可得出Ri=(0+0.5)/2=0.25。然后进行第2次迭代计算,如果D1 图8 二分法创建等距点 RL=0'比例下限 RU=1'比例上限 Ri=0.5'初始比例 For j=1 To 30'循环30次 If Abs(D1-D2)<δ Then'小于等距判定阈值δ则终止运行 Exit For End If If D1>D2 Then'距离判定 RL=RL RU=Ri Ri=(RL+RU)/2 Parameters.Item(1).Value=Ri'调整点在直线上的比例参数 Else RL=Ri RU=RU Ri=(RL+RU)/2 1.6 统计学分析 Meta分析采用RevMan 5.3版本软件进行。二分类数据采用相对危险度(relative risk,RR)和其95%CI作为统计量;连续型数据采用标准均数差(standardized mean difference,SMD)和其95%CI作为统计量。首先使用χ2检验和I2检验对各研究间的异质性进行评估,若P>0.1且I2≤50%,说明各研究间同质性较好,采用固定效应模型,否则采用随机效应模型进行合并。此外,根据研究的干预措施的不同进行亚组分析;根据主要结局指标“临床疗效”绘制漏斗图检验发表偏倚情况。 Parameters.Item(1).Value=Ri End If Next 在曲线L1、L2上按给定的步长λ,分别创建n个等分点,如图9所示。 图9 等分点 将曲线L1、L2上的等分点成对连接成n条直线,如图10所示。 图10 连接等分点 创建每条直线的中点Pi,如图11所示。 图11 中心点 使用上述二分法调整中点Pi在直线上的比例参数,使Pi与两条直线的距离相等或小于阈值δ,将所有调整后的Pi连成样条曲线,即得到曲线间的中心线L,如图12所示。 图12 中心线 董箭等[10]对曲线间中心线的生成算法进行了分析和评估,总结得出Delaunay三角网格法不符合中心线的数学定义,无法满足精度较高的应用需求,相比缓冲区边界相向逼近求交法,单位圆滚动法在精度、效率及中心线形体控制等方面均明显占优,是曲线间中心线生成的优选方法。经综合考虑,将本文所提方法创建的中心线,着重与单位圆滚动法及内切圆法创建的中心线作比较。 通过测量本文所提方法创建的中心线L上的任意点Pi与两条曲线的距离(图12),可以得到其误差为0.003 mm,小于给定的阈值δ(δ=0.02 mm),运行时间约为4.055 s。 将单位圆半径R设为10 mm,等距判定的阈值δ=0.02 mm,采用单位圆滚动法生成了如图13所示的中心线L。经过测量得出该中心线误差为0.001 mm,运行时间约4.583 s,中心线较为完整和光顺。 图13 单位圆滚动法生成的中心线 采用内切圆法生成了如图14所示的中心线L。经过测量得出该中心线误差为0 mm,运行时间约0.672 s,计算速度非常快,但因端部产生异常内切圆,需通过人工专门识别和处理,得到的中心线不完整,也因内切圆分布的不均匀,可能导致非锚点拟合区域的中心线精度不足。 图14 内切圆法生成的中心线 综上所述,本文所提方法创建的中心线与单位圆滚动法创建的中心线精度和计算速度均相当,但后者需要专门定义单位圆半径R和绘制起始点,否则可能出现无解或精度不足的情况。与内切圆法相比,本文所提方法计算速度不如它,但内切圆法创建的中心线可能不完整,需要人工专门进行后处理,一定程度上影响了它的使用效率。 某复合材料导弹弹翼的截面如图15所示。由于该弹翼为非对称结构,但又需在其中性面上进行对称铺层设计,因此首先需要按本文所提方法创建中心线,如图15所示。 图15 某弹翼截面示意图 对于等截面翼型,可将中心线直接拉伸成中性面,然后在中性面上进行对称铺层设计,如图16所示。对于非等截面翼型,可以通过在多个不同截面上创建多条中心线,再将这些中心线拟合成曲面,并对曲面进行光滑处理[11],得到光顺准确的中性面。 图16 某弹翼铺层示意图 后续进行了该弹翼的试制,零件脱模顺利,表观质量良好,如图17所示。 图17 某弹翼实物 本文提出一种自动创建曲线间中心线的新方法,该方法基于等距原则和有限元法,采用VB语言编制程序,自动创建曲线间的中心线,且中心线的精度可按需调整,计算速度较高,运行稳定,不需专门进行前期预处理和后处理,并通过实例验证了所提方法有效可行。按该方法创建的中心线准确光顺,可以满足设计和使用要求。而且在创建中心线的过程中,大部分重复繁琐的工作均通过编制宏程序由计算机自动执行,提高了工作效率,降低了劳动强度,值得推广应用。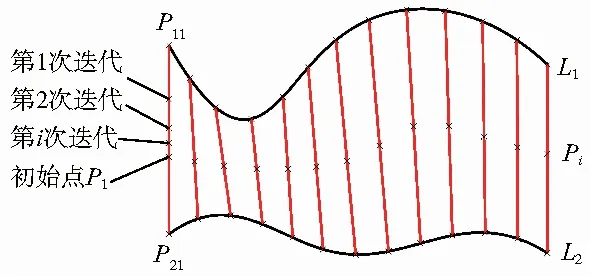
2 解决方法
2.1 创建等分点

2.2 连接等分点

2.3 创建中点

2.4 创建中心线

2.5 结果分析和对比


2.6 实物验证



3 结语
