锂电池极片辊压机刚度分析与结构优化

马嵩华　田　凌

1.山东大学,济南,250013　　2.清华大学,北京,100084

锂电池极片辊压机刚度分析与结构优化

马嵩华1田凌2

1.山东大学,济南,2500132.清华大学,北京,100084

在锂电池极片加工过程中，由于其高能量密度要求与涂覆材料力学性能存在矛盾，故需要根据极片所需压缩比严格控制辊压力的大小，而实际中,轧辊特性使两辊之间窄缝距离的直接测定不容易,因此难以通过物理样机试验的方式直接得到生产过程中辊缝与辊压力之间的关系。针对该问题，简化了辊压过程中的物理量,建立了整机和极片变形的数学模型，利用数学模型间接得到整机辊压力与辊缝变化之间的定量关系。采用仿真驱动设计的方式，基于响应面法和多目标优化算法得到整机的设计优化结果。测试试验表明,简化的数学模型可以数字化地描述辊压机的工作情况，便于指导生产中控制极片的制造工艺参数，同时基于响应面的设计优化提高了辊压机的设计生产效率。

辊压机；锂电池极片；有限元分析；优化设计

0　引言

人们对移动设备日益增长的需求对电池提出了高能量密度、长循环寿命、高电压、安全、低廉等要求。为提高电池储能能力，保证极片材料的压实程度，需要对极片进行辊压。极片辊压机作用的对象为厚0.2 mm左右的电池极片,表面精度几微米,以铝箔和铜箔为基体,上面涂覆活性物质，表现出复杂的弹塑性变形，轧制过程要求压力可以从1.03 MN(103 t)到0.6 MN(60 t)变化。目前,锂电池厂家采用试错法确定轧制工艺参数,该方法工作效率低,且造成大量的人力物料浪费。

国内外研究辊压机整机的仿真还很少,主要针对机床和加工中心[1-3],或针对轧辊与被轧物之间的局部作用过程[4-7]。传统辊压机的刚度相对被轧物刚度要大很多,整机可以看作刚体不变形进行研究；而对于极片轧制,整机变形量对于其表面一致性和材料的压实密度有很大的影响,直接影响电池的性能。针对轧制对象的复杂性和工艺参数的控制要求,本文对锂电池极片辊压机轧制过程进行建模仿真和分析,建立整个轧制系统辊压力与实际极片压缩量之间的关系，为定量控制极片制造工艺参数提供保证；同时采用仿真驱动设计的方式，对整机进行建模优化，以提高辊压机设备的设计生产效率。

1　极片压缩与辊压机变形关系

对锂电池极片进行仿真分析,需要建立极片压缩比、辊压力与双辊辊缝之间的数值关系,这样才能够定量地控制极片辊压过程的工艺参数。整个辊压机主机主要包括：辊系、轴承、轴承支座、机架、液压缸和调整辊缝大小的楔形块以及连接机构。

图1所示是以极片理想压缩量Δxi为输入、极片实际压缩量Δxo为输出时系统的数学模型,其传递函数如下：

(1)

式中，G1为极片的压缩比与辊压力之间的关系系数；G2为辊子刚度；K1、Ka分别为机架、轴承刚度。

图1　辊压机系统方块图

图1中，F1～F4为各模块之间传递的力关系,Δx1～Δx4为各模块之间传递的位移变形关系。

由于辊压机的输入转速慢、工作状态较为平稳，故可以将工作过程看作静态进行分析。在静态力学分析时，辊压力通过轧辊、轴承、轴承座，最终传递到机架上。通过求解G1、G2、K1和Ka即可定量求出Δxo。

1.1辊压机数学模型

1.1.1轴承刚度等效

滚动轴承的刚度一般可定义为轴承内外套圈产生单位的相对弹性位移量所需的外加负荷。滚动轴承的滚子与滚道之间的接触看成纯粹的Hertz接触。计算轴承轴向刚度ka和径向刚度kr的经验公式[8]为

(2)

(3)

其中,Fa为轴承承受的轴向力，Fr为承受的径向力，其他符号解释见表1。型号LDHY600-N60的辊压机采用四列向心短圆柱滚子轴承,其等效参数取值见表1。计算得到的整个轴承径向刚度为20 073N/mm，轴向刚度为7062N/mm。有限元分析时轴承使用圆周相位差120°的三个弹簧并联等效。

表1　轴承等效参数

1.1.2整机有限元分析结果

辊压机生产线结构复杂,建立仿真模型时只考虑主机部分,辊压机系统由机架、轧辊、液压油缸、楔块、轴承及轴承座等部件组成。辊压机机架材料为45钢，上下轧辊材料为9Cr2Mo，上下轴承座材料为ZG45，其他零部件材料为45钢。划分网格时选择四面体单元自由划分，有限元模型如图2所示，模型中共有节点134 160个，单元55 325个。

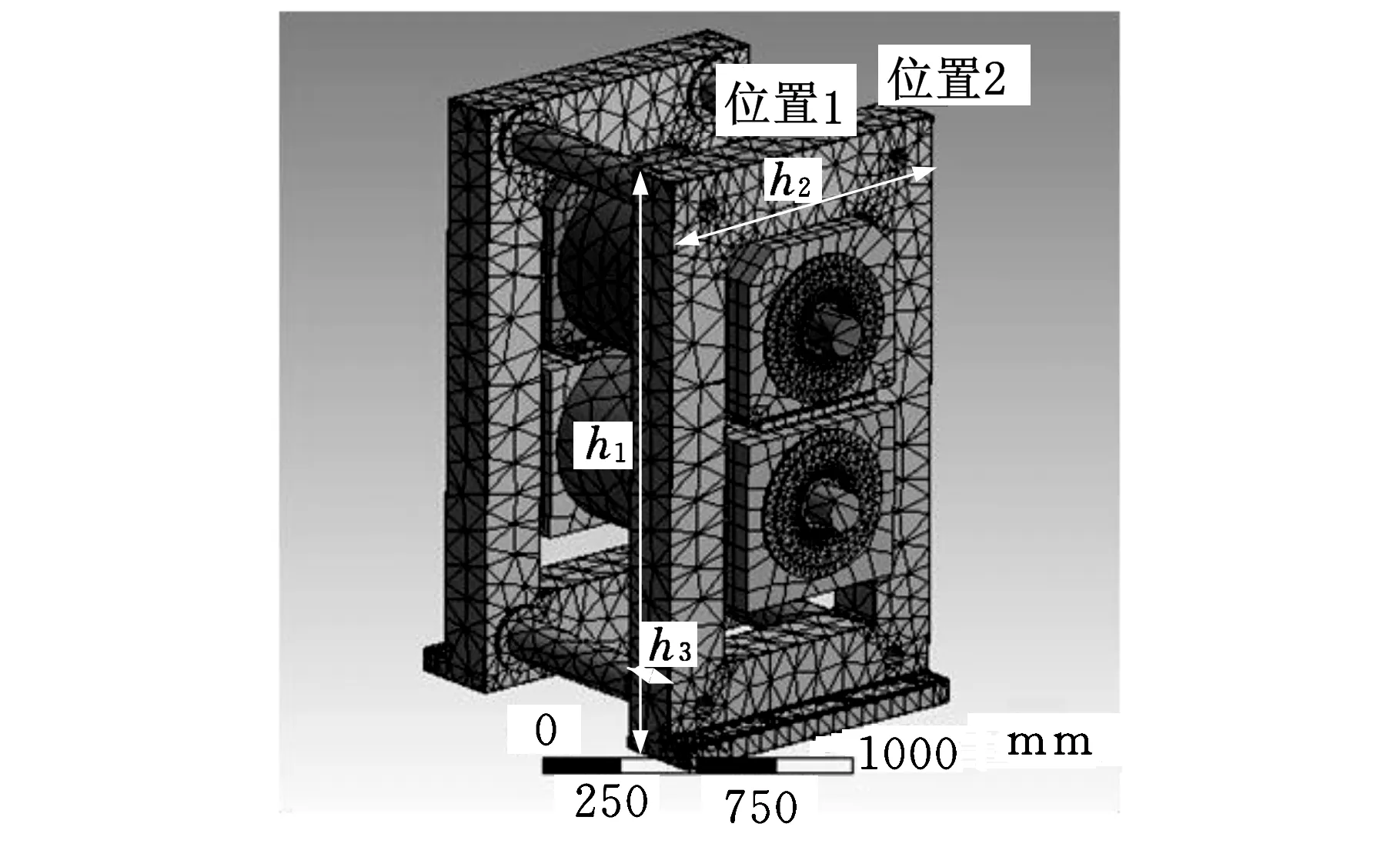
图2　整机有限元模型

有限元分析时将机架底面固定,在两个下轴承座上分别施加250～1500 kN作用力,在安装液压缸的机架上相应地施加反向作用力；在上下轧辊与极片接触的7 mm宽的窄带上施加1000 kN的作用力,模拟极片受到的辊压反作用力。载荷的位置与实际工作情况对应,得到整机载荷与图2标示位置变形之间的关系,如图3所示。

图3　数字模型的测试点变形

1.1.3整机试验结果

对同型号辊压机进行变形测试试验。在物理样机同图 2的位置上安装千分表。液压缸逐步加载6组试验压力得到不同测试点的位移形变,如图4所示。比较物理样机和数字模型之间在变形量上的结果偏差,如表2所示。

图4　物理样机测试点变形

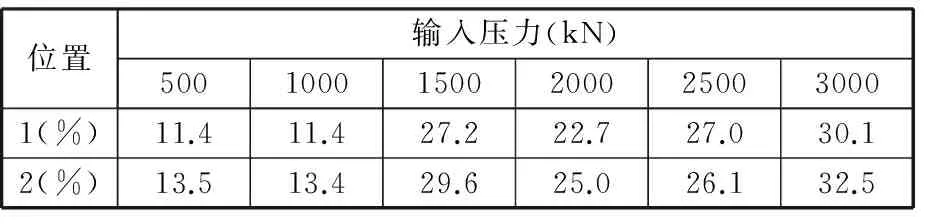
位置输入压力(kN)500100015002000250030001(%)11.411.427.222.727.030.12(%)13.513.429.625.026.132.5

Zhang等[9]研究表明固有频率是验证数字模型准确性的一个重要指标。对辊压机进行模态实验,用激振器从不同方向对整机进行激振,激振信号为正弦扫频,扫频范围为30～500 Hz，处理得到拾振点所测的加速度信号频响函数，与数字模型的仿真固有频率进行对比,得到如表3所示的结果。由于在有限元模型中存在一部分连接被定义为刚性,因而整机固有频率的仿真值大部分较试验值略大。所建立的数学模型与实际情况比较吻合，说明上述数字模型可以代替物理样机进行试验分析和设计优化。

表3　辊压机固有频率有限元分析值与测试值

1.2极片“辊压力-压缩量”关系

金属辊压工艺常被视为短暂的弹塑性变形过程,而极片这种在基体上涂覆多种化合物材质的压缩变形情况要复杂得多，此处简单地抽象为5个阶段:①“坍塌”期，从极片接触辊面开始，至极片内部的孔洞被填补完为止;②初步压缩期,坍塌结束后，微粒团间相互发生碰撞和挤压;③剧烈压缩期，极片内各微粒团继续向辊缝中心运动，直至辊缝最小处，微粒团相互剧烈挤压，发生形变甚至破坏，随着压力的增加，长链的粘结剂会打开甚至断裂，从而影响电芯的循环性能;④受控恢复期，从辊缝最小处开始，所受压力不断减小，极片发生一定程度的恢复;⑤自然恢复期,极片脱离辊面，在自身新弹性系数下进行恢复。

极片辊压微观变形情况复杂,甚至在表面附近有一层大致5 μm的致密层。为保证孔洞的坍塌效应得到体现,此处采用粉末冶金材料等效极片涂覆材料。粉末冶金材料由于内部孔隙的存在,在塑性变形时除形状变化外还伴有体积的变化。因为其屈服应力除了与应力偏量有关外，还和静水应力有关，因此Mises屈服准则对粉末冶金材料不再适用。此处在“可压缩连续体”的假设上,使用Gurson[10]模型定义粉末冶金材料的屈服条件,即：

(4)

式中,q为有效Mises应力;p为静水压强;σy为全密度材料的屈服应力;γ为空穴体积比。

对于锰酸锂(LiMn2O4)涂覆的正极电池极片,其仿真等效参数值为：密度1120 kg/m3、相对密度0.4、弹性模量15 GPa、泊松比0.3、屈服强度16.872 MPa。

1.3轧制过程“辊压力-压缩量”关系

通过上述假设得到极片“辊压力-压缩量”之间的关系,这里的辊压力并不是实际作用在轧辊上力的大小。借鉴冷轧薄材的轧制力计算数学模型,如柯夫冷轧轧制力公式、斯通平均单位压力模型、Bland-Ford-Hill显隐式模型、Bryant和Roberts单位宽度模型[11]等，可以获得轧制过程中的辊压力。假设轧制过程中极片厚度、前后张力、轧辊转速以及温度等恒定不变，只考虑极片出口厚度的变化，可得到辊压力[12]为

(5)

(6)

根据已建立的有限元模型,得到不同输入压力(50～300kN)下的“辊压力-辊缝”关系,对应图5中平行的斜线组；根据上述假设建立的极片“辊压力-缩量”关系,对应图5中压缩量曲线。由于辊缝变形量Δ1和极片压缩量Δxo之间存在Δ1+H0=0.2-Δxo的关系(H0为初始辊缝),因此,随H0的增加,图5中极片压缩量曲线向下平移。两种曲线的交点即为零辊缝下对应输入压力下辊压机作用于极片的辊压力,并可通过辊缝变化量间接得到实际极片的压缩量。图5对于指导辊压极片生产过程具有重要意义。在给定辊缝、保证极片压缩比的条件下，确定液压缸应提供的输入压力,从而有效地控制输入能源的量值。

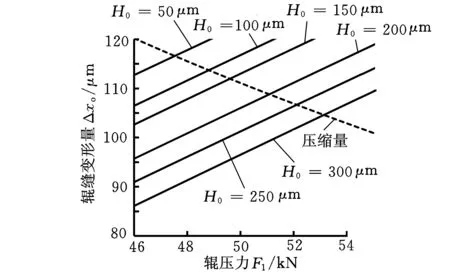
图5　整机系统“辊压力-压缩量”关系

2　辊压机设计优化

设计的不合理会造成整机刚度降低，进而影响极片的加工精度和生产效率。如果每个设计参数各个候选取值对结果产生的影响均通过仿真进行分析，则计算量巨大，而且不能确定每个参数对结果的影响程度，更难以寻找最优解。本节以辊缝变形量最小为目标，对各设计参数进行优化。

2.1基于响应面法的优化流程

响应面法(response surface methodology,RSM)是基于试验结果建立因素与指标的关系模型[13]。已有许多研究基于响应面开展了设计优化[14-15]。基于响应面法的优化设计步骤见图6。

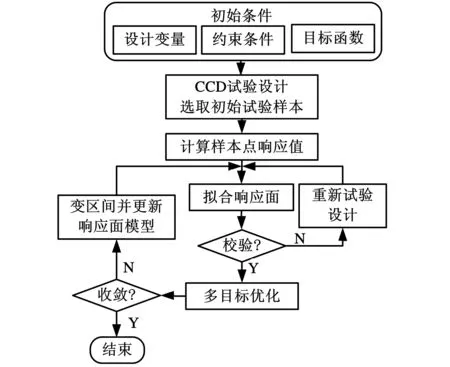
图6　基于响应面法的辊压机优化设计流程

(1)确定设计变量及设计目标。选取影响辊压机整机刚度的重要参数作为设计变量,以减小辊缝变形量作为优化目标。

(2)构建响应面模型并检验模型的准确性。设计变量和目标确定后，使用中心复合设计(central composite design,CCD)进行试验设计,得到不同设计变量值的组合以及相应的目标结果。运用最小二乘法获得目标函数的二次响应面近似模型：

(7)

其中,z为输出目标,yi为设计变量,m为设计变量的个数,βi j为待定系数,υ为误差;为检验响应面的精确性,对试验设计得到的近似模型的近似值做拟合度检验。若校验通过,可利用该二次响应面近似模型进行优化,反之须重新设计试验。

(3)基于响应面模型进行优化并验证结果。利用满足精度要求的响应面近似模型代替真实的有限元模型进行优化,获取优化值,其数学模型为

(8)

其中,fi(X)为要考察的目标,gk(X)与hl(X)为约束。采用非支配排序遗传算法Ⅱ(NSGA-Ⅱ)对该模型进行求解。

2.2辊压机主机结构优化

按照上述设计优化流程,对辊压机的机架部分进行优化,除轧辊定制参数外的其他参数随着设计变量的改变而变化。分别选取机架高度y1、机架宽度y2、机架厚度y3、液压缸输入压力y4和辊缝之间的压力y5为优化变量,对应的初值分别为1976 mm、1097 mm、196 mm、9.53 MPa和1000 kN。其中前三个参数为设计优化参数,指导整机设计研发过程;后两个为工艺优化参数,指导辊压极片过程控制。设计五因素CCD,获取27个样本点。将辊缝变形量z作为研究对象,得到辊缝的试验结果见表4。

表4　CCD和试验结果

根据最小二乘拟合得到二次多项式响应面,表达式为

z=0.0348-0.0770y1-0.3421y2+0.2574y3-

10-4y1y4+0.0156y1y5+0.0033y2y3+

0.0037y2y4+0.0673y2y5+1.70×10-5y3y4-

0.0011y3y5-1.49×10-5y4y5

为验证二次多项式拟合方程显著性,进行拟合度检验。拟合度检验值为13.26,大于F0.02(21,5)=6.99,结果表明回归方程拟合得较好。

由图7可以观察到不同因素间的交互影响对辊缝变化的影响趋势,也可以方便观察到使辊缝变形量最优时各因素的取值范围。图7a显示随着机架横梁升高和宽度的增加,整机刚度增加,辊缝变形越来越小,y1对于辊缝变形的影响比较强烈。图7b则是机架宽度y2与y3联合作用对于辊缝变形量的影响。液压缸输入压力y4和辊缝之间的压力y5对于结果的变形量影响是负相关的,辊缝变形随着两者的增加而等比例增大。

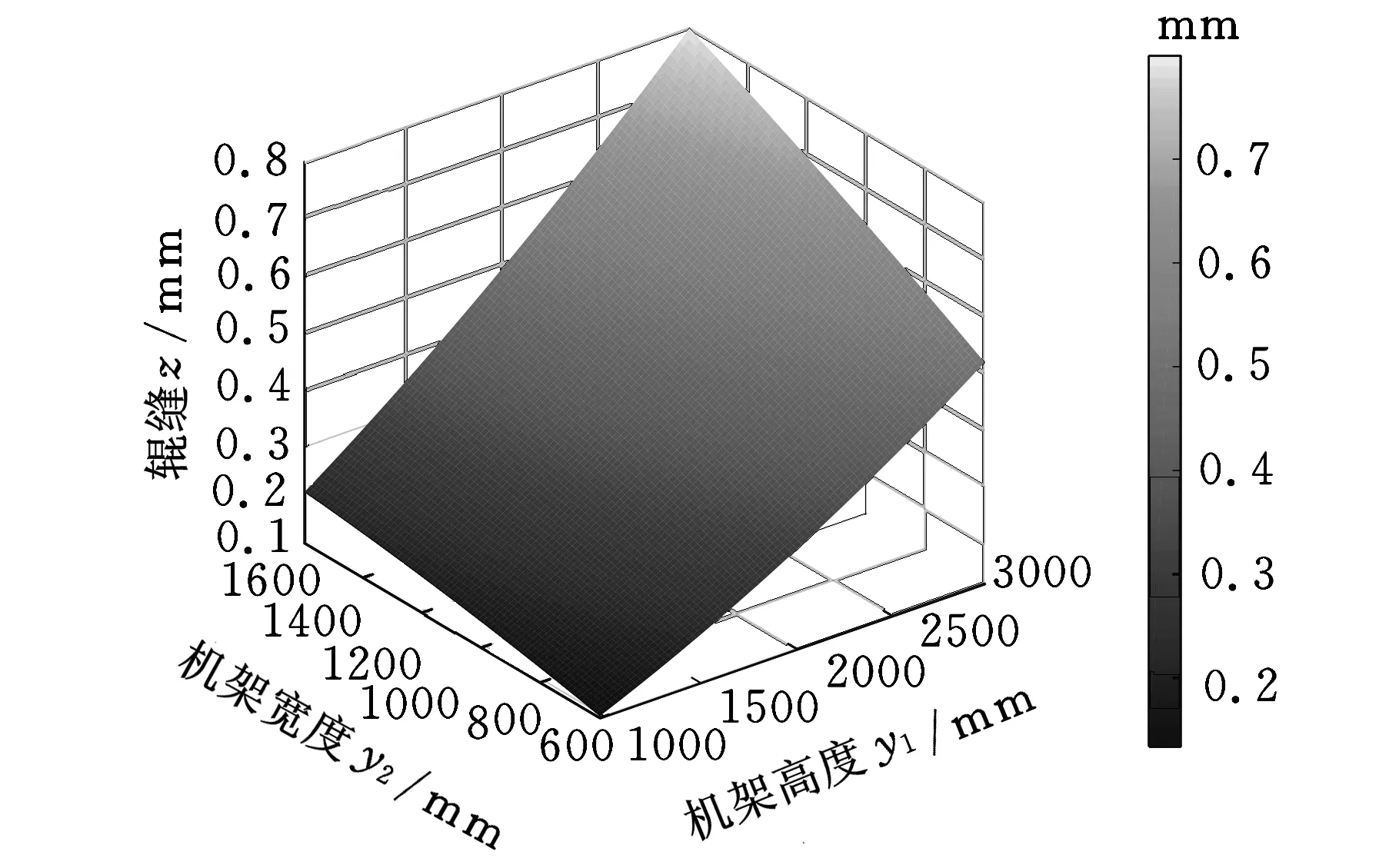
(a)y1与y2交互曲面

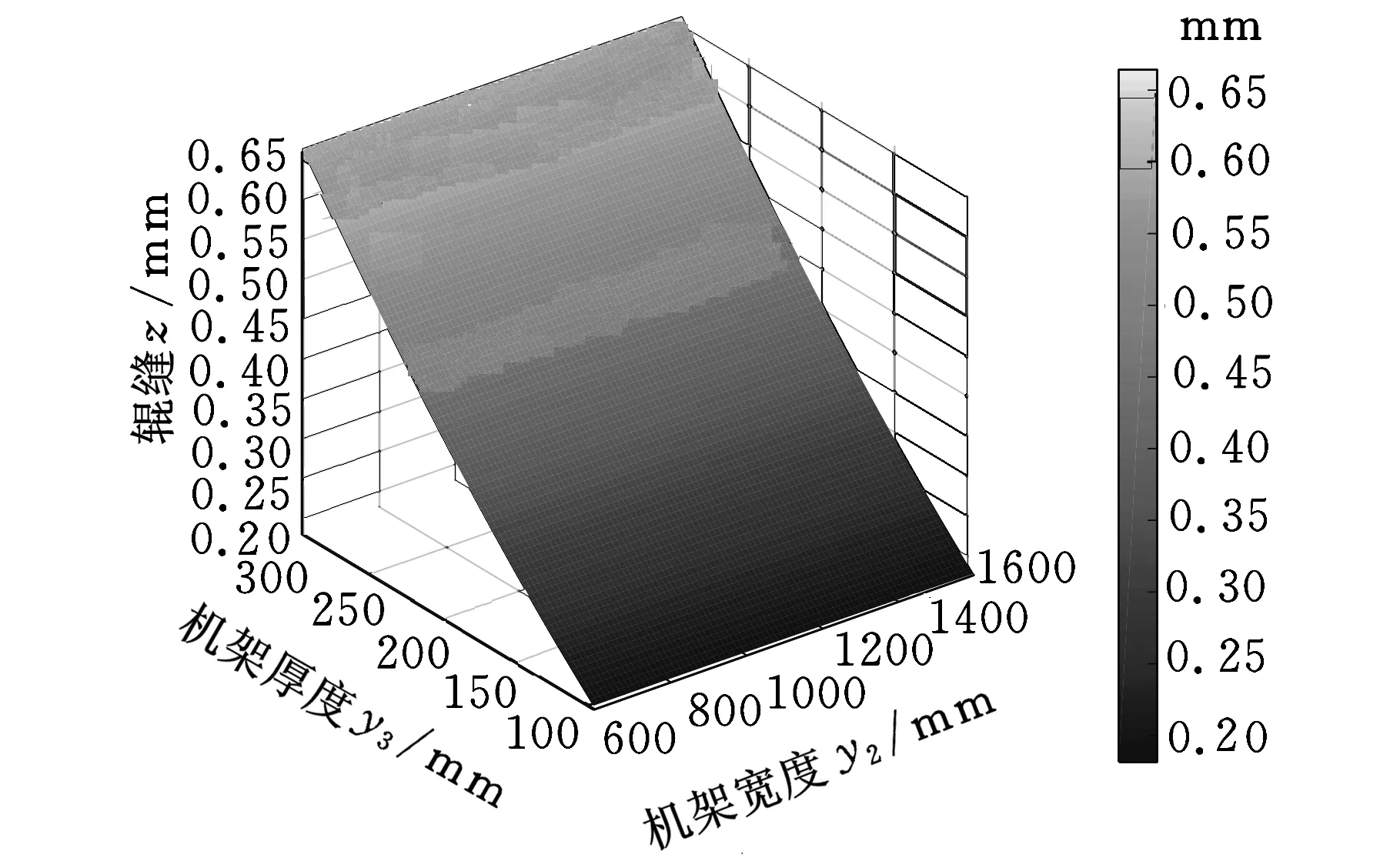
(b)y2与y3交互曲面图7　不同设计参数的二次响应面

通过NSGA-Ⅱ计算,辊缝变形量最小的三个设计结果如表5所示。优化结果可以在保证辊缝变形量最小和整机刚度的前提下,得到最省材料的设计结果和最省能源的工艺生产方式。以候选优化结果1为例,相较于原型机在质量上减小了15.0%,而载荷值减小了74.9%;由于辊缝之间的压力也减小了,故该优化结果可以用于加工材质较软的阳极极片。

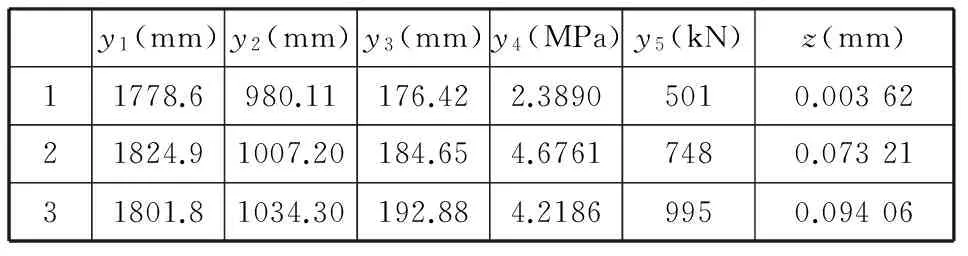
表5　整机优化结果

3　结论

(1)建立了辊压机整机的有限元模型。试验验证了该模型与实际辊压机物理模型结果基本一致，可代替物理样机进行系统分析。

(2)将有限元方法引入到极片轧制过程的分析中,对涂覆层力学参数进行预测。根据仿真得到的辊压机整机“辊压力-辊缝变形”关系与极片的“辊压力-压缩量”关系可以实现定量控制极片轧制厚度。

(3)对有限元模型进行基于响应面的分析,得到整机主要设计参数之间的定量关系,同时得到多目标优化结果,为后续辊压机设计提出改进方向,有利于迅速开展产品设计和分析。

[1]孙明楠,殷国富,胡腾,等.基于广义动态信息模型的机床结合部动刚度参与因子辨识方法[J].机械工程学报,2013,49(11):61-69.

Sun Mingnan, Yin Guofu,Hu Teng,et al.Method of Dynamic Stiffness Participation Factors Identification of Machine Tool Joints Based on the Generalized Dynamic Information Model[J]. Chinese Journal of Mechanical Engineering,2013,49(11):61-69.

[2]李殿新,赵沿民,张建富,等.立式加工中心静刚度细化试验与有限元分析[J].农业机械学报,2012,43(12):262-267.

Li Dianxin,Zhao Yanmin,Zhang Jianfu,et al.Fine Experiment and Finite Element Analysis for Static Stiffness of Vertical Machining Center[J].Transactions of the Chinese Society for Agricultural Machinery,2012,43(12):262-267.

[3]彭艳华,管贻生,张宪民,等.基于复合优化方法立式数控加工中心的多目标优化设计[J].振动与冲击,2012,31(6):48-52.

Peng Yanhua,Guan Yisheng,Zhang Xianmin,et al.Multi-objective Optimization Design for a Vertical Machining Center Based on Composite Optimization Method[J].Journal of Vibration and Shock,2012,31(6):48-52

[4]刘浩然,侯东晓,时培明,等.轧机辊系滞后非线性垂直振动系统的振动特性[J].机械工程学报,2011,47(13):65-71.

Liu Haoran,Hou Dongxiao,Shi Peiming,et al.Vibration Characteristics of Hysteretic Nonlinear Vertical Vibration System of Rolling Mill Roller[J]. Chinese Journal of Mechanical Engineering,2011,47(13):65-71.

[5]甘建国.高压对辊粉碎的微分剪切理论及数学模型[J].机械工程学报,2008,44(3):241-248.

Gan Jianguo.Differential Shear Theory and Mathematical Model of High Pressure Double Roll Crush[J].Chinese Journal of Mechanical Engineering,2008,44(3):241-248.

[6]Niroomand M R,Forouzan M R,Salimi M,et al.Experimental Investigations and ALE Finite Element Method Analysis of Chatter in Cold Strip Rolling[J].ISIJ International,2012,52(12):2245-2253.

[7]王东城,彭艳,刘宏民.冷轧带钢平整机高精度高速度轧制力模型开发[J].塑性工程学报,2008,15(1):172-177.

Wang Dongcheng,Peng Yan,Liu Hongmin.A High-resolution High-speed Rolling Force Model for Cold Strip Temper RollingMill[J].Journal of Plasticity Engineering,2008,15(1):172-177.

[8]机床设计手册编写组.机床设计手册[M].北京:机械工业出版社,1979.

[9]Zhang G P,Huang Y M,Shi W H,et al.Predicting Dynamic Behaviours of a Whole Machine Tool Structure Based on Computer-aided Engineering[J]. International Journal of Machine Tools & Manufacture,2003,43(7):699-706.

[10]Gurson A L. Continuum Theory of Ductile Rupture by Void Nucleation and Growth:Part I-Yield Criteria and Flow Rules for Porous Ductile Materials[J].Journal of Engineering Materials and Technology,1977,99(1):2-15.

[11]采利科夫.轧钢机的力参数计算理论[M].北京:中国工业出版社,1965.

[12]杨节.轧制过程数学模型[M].北京:冶金工业出版社, 1993.

[13]何为.优化试验设计方法及数据分析[M].北京:化学工业出版社,2012.

[14]马劲红,张文志,宋剑锋,等.MOGA和FEM相结合实现万能型钢轧机机架圆角的多目标优化[J].塑性工程学报,2008,15(1):146-149,177.

Ma Jinhong,Zhang Zhiwen,Song Jianfeng,et al.Multi-objective Optimization of the Housing’s Fillet Angle of the Universal Rolling Mills using MOGA Combined with FEM[J].Journal of Plasticity Engineering,2008,15(1):146-149,177.

[15]于海莲,王永泉,陈花玲,等.响应面模型与多目标遗传算法相结合的机床立柱参数优化[J].西安交通大学学报,2012,46(11):80-85.

Yu Hailian,Wang Yongquan,Chen Hualing,et al.Optimization for Machine Tool Column Combining Response Surface Model with Multi-objective Genetic Algorithm[J].Journal of Xi’an Jiaotong University,2012,46(11):80-85.

(编辑袁兴玲)

Stiffness Analysis and Structure Optimization of Rolling Mill for Lithium-ion Battery Electrode Manufacturing

Ma Songhua1Tian Ling2

1.Shandong University,Jinan,2500132.Tsinghua University,Beijing,100084

In the process of rolling electrodes,due to the contradiction between the energy density and the material mechanical properties of coatings on the electrode,the roller pressure should be controlled strictly according to the compression ratio.Actually,the roller surface made the gap between two rollers difficult to measure through experiments.Consequently,it was difficult to directly quantify the relation between the gap size and roller pressure by using physical prototype.The variations of physical quantities during the electrodes manufacturing process were simplified to build the digital model of rolling mill and electrode deformation.With the help of the digital model,the relation of gap variation and pressure was quantitatively simulated.According to the above study, on the purpose of simulation-driven design,the structural parameters and work condition of digital rolling mill were optimized by the response surface methodology and multi-objective genetic optimization algorithm.The stiffness test has validated the digital model and the simplification hypothesis.These results are important to lay a plan for rolling processes;meanwhile the research and development efficiency is improved by the response surface-based design optimization.

rolling mill;lithium-ion battery electrode;finite element analysis;optimization design

2013-08-20

国家自然科学基金资助项目(51175287)

TG333.1;TB472DOI：10.3969/j.issn.1004-132X.2015.06.018

马嵩华,女,1985年生。山东大学机械工程学院助理研究员。主要研究方向为协同设计、知识工程。发表论文8篇。田凌,女,1963年生。清华大学机械工程系教授、博士研究生导师。