基于随机子空间法和固有频率法的线路故障定位
2015-10-28张凯
张 凯
(山东省电力公司潍坊供电公司,山东潍坊261061)
基于随机子空间法和固有频率法的线路故障定位
张 凯
(山东省电力公司潍坊供电公司,山东潍坊261061)
输电线路发生故障后,进行准确快速的故障距离判断在实际生产运行中具有很大的意义。线路故障后,将产生一系列的故障暂态行波,且从频域的角度看,行波可看作为谐波形式。提出基于随机子空间法和行波固有频率法相结合的方法进行线路故障定位。首先通过相模变换得到输电线路中的模电流分量,然后基于随机子空间算法进行辨识得到行波固有频率,进而计算此频率下的行波波速和模阻抗导纳矩阵,最后可求得故障距离。在PSCAD中搭建两端系统仿真模型,经过仿真验证表明,此方法可有效进行线路故障定位,且准确度较高。
故障定位;随机子空间;固有频率法;行波
0 引言
输电线路是电力系统中最容易发生故障的地方,准确的故障定位进而进行故障清除可有效缩短故障时间,很大程度上提高了电力系统稳定性。如何准确的故障定位,是故障清除的基础,也是维持电力系统稳定性的基础。对输电线路故障定位方法的研究最早可追溯于20世纪30、40年代[1]。线路故障定位的方法有很多,按照变量信息获取的方式,可分为单端法和双端法;按照计算故障距离的原理不同,亦可分为故障分析法、行波法、阻抗法和电压法[2]。其中行波测距方法是目前应用发展比较广泛的方法,但提取故障行波波头具有较大的困难[3],主要是由于行波色散问题导致的波头捕捉较为困难[4]。单端行波测距的难点在于能否准确区别出故障反射行波和其他线路反射行波,双端行波测距的难点在于准确测量出第一个行波波头到达时间[5,6]。
鉴于此,可采用行波固有频率[7~10]的故障定位方法来进行故障测距。当线路发生故障时,在输电线路中会形成很多故障暂态行波,并在频域上表现为谐波形式,其本质即为行波在线路两端多次反射和有限长度线路的延时效应共同作用的结果,被称之为固有频率。采用固有频率法进行故障定位的基础是对线路暂态行波的固有频率进行准确辨识,常用方法是利用快速傅里叶变换(Fast Fourier Transform,FFT)[11~13]来对故障电流或电压进行频谱分析。但FFT的频域分辨率较低,无法准确提取行波的固有频率。文献[14]提出利用Prony算法提取故障电流中的暂态行波固有频率,但Prony进行辨识时,对系统阶数拟合较为困难,尤其是目前的大电网系统中,容易引发“维数灾”问题。文献[8]提出复小波对故障后电流或电压信号进行连续小波变换,进而对小波参数进行后处理以提取主自然频率,但小波变换中存在小波基波选取困难的问题。
鉴于此,文中提出采用随机子空间法(Stochastic Subspace Identification,SSI)[15,16]来分析故障电流中暂态行波的自然频率。SSI通过构造Hankle矩阵,进行SVD分解,使之算法本身具有一定的抗噪能力,在实际电网中更能准确辨识出暂态频率参数。文中首先采用PSCAD/EMTDC搭建简单三相长距离输电线路,并在一定距离内施加三相接地短路故障,进一步根据相模变换得到线路的模电流,然后采用Matlab软件编写SSI辨识程序,以辨识出故障模电流中的固有频率,进而可准确算得行波波速和故障距离。
1 基本原理
由于行波在输电线路中从频率的角度考虑即为谐波形式,故而可将行波固有频率的辨识看做谐波频率的准确辨识。
电力系统中的谐波信号可拟合为:
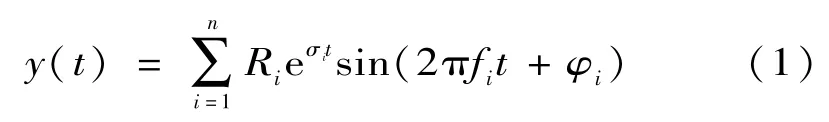
式中:Ri为幅值;fi为角频率;φi为初相;σi为衰减因子。
1.1 随机子空间理论
SSI核心是把“将来”的输出行空间投影到“过去”的输出行空间,投影结果是保留了“过去”的全部信息,并用此预测“将来”。SSI复杂度低,因为只运行一次SVD分解,故而运算效率高。
对于白噪声激励的线性系统,随机状态空间模型可以表示为

式中:yk∈Rl×l为第l个测点,在第k(k∈N)个采样间隔(Δt)的输出向量;xk∈Rn×l为系统的状态向量,n为系统的阶数;A∈Rn×n为系统矩阵;C∈Rl×n为输出矩阵;wk∈Rn×l为系统噪声污染;vk∈Rl×l为测量噪声;wk和vk互不相关。
根据系统输出yk构造Hankel矩阵H

式中:Y0/2i-1的下标0/2i-1表示Hankel矩阵第一行块和最后一行块;下标p和f分别表示“过去”和“将来”。
定义输出yk自协方差矩阵Ri为

由协方差序列组成的Toeplize矩阵T1/i为

对矩阵T1/i进行奇异值分解,秩为非零的奇异值个数,即为系统阶数。

式中:S1∈Rli×n;V1∈Rn×n;D1∈Rli×n;n表示系统阶数,阶数可用SVD分解法确定。通过SVD分解可得到奇异值,根据奇异值突变确定系统模态阶数,若取得阶数过大,会出现过拟合现象,生成虚假模态,降低了模态辨识的准确性;若取得阶数过小,有可能出现漏辨识现象,丢失重要模态信息。
Tq/i可分解为

式中:Oi为可观矩阵;Γi为反转随机可控矩阵。
根据上式可得到系统矩阵A和C。

对系统矩阵A做特征值分解

式中:Λ=diag[λ1,λ2,…,λ1…,λn]∈Cn×n,λi为系统特征值;Ψ=[ψ1,ψ2,…,ψn]∈Cn×n为系统特征向量矩阵;n表示系统阶次。
可通过式(10)计算出谐波的角频率和衰减系数

进而通过最小二乘得到各次谐波的幅值和相角对于N个采样数据存在

其中

式中:n表示得到的谐波个数。
则P的最小二乘解为
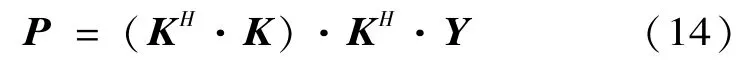
则各变量的幅值Ri和相角φi可求得为

由此已经求得各谐波量的幅值、频率、相角。
1.2 行波固有频率
线路上的故障行波信号具有从低频到高频的连续波谱,其中某些频率分量与故障行波传播的路径及其边界条件有一定关系,称之为故障行波的固有频率[9]。由文献[10]知,输电线路中暂态行波的固有频率为

式中:Γ1和Γ2分别为测距端和故障端的反射系数,大小均由测距端和故障端的阻抗决定;θ1和θ2分别为Γ1和Γ2对应的幅角;d表示故障点到测距点的距离;v表示暂态行波在固有频率下的传播速度。且存在

其中,k=0,±1,±2,…。
则固有频率大小为

衰减系数为
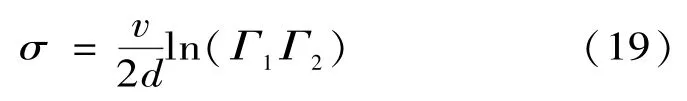
则故障测距可由式(18)表示为

由此可知,只要辨识出行波固有频率,并计算得到固有频率下的行波速度、测距端和故障端的反射系数的幅角即可准确计算出故障距离。
1.3 故障测距
实际交流输电线路一般为有损的三相电路,各项之间存在耦合,需进行电压、电流的解耦,常用的解耦方式为相模变换,即

式中:Tu和Ti分别为电压和电流的变换矩阵;Um和Im分别为电压和电流相模变换后的量,即模量。
由于交流三相输电线路是对称线路,故一般可取Tu=Ti,可取变换矩阵为

式中:变换矩阵中的列向量分别表示0,β和α模变换向量。对于输电线路在固有频率f下的导纳矩阵Z和阻抗Y矩阵亦需进行相模变换,变换后的模导纳矩阵Zm和模阻抗矩阵Ym可表示为。

则输电线路的模特征阻抗矩阵可表示为

由文献[17]知,行波的模波速为
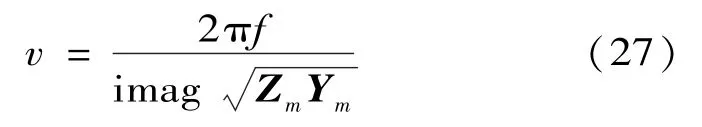
则在行波固有频率下测距端和故障端的反射系数即其幅角可表示为

式中:I表示单位矩阵;Z1表示系统本段等效阻抗矩阵;Yf表示故障点导纳矩阵。假设系统等效阻抗矩阵呈感性且为三角对阵矩阵,则在行波固有频率f下可表示为

对于模信号的选取,三相接地短路和相间短路可采用β模电流分量作为辨识信号。
2 仿真分析
为验证文中所采用方法的有效性,在PSCAD/EMTDC软件中搭建两端220 kV输电线路,拓扑结构图如图1所示。

图1 拓扑结构图
图1中,EA和EB是两个理想电压源,电压等级分别为220∠50 kV和218∠30 kV,A和B端的系统阻抗分别为

A与B之间采用架空输电线,线路类型选用TOWER:3H5杆塔,线路长度为500 km,采用四分裂导线,完全换位,参数采用PSCAD中的默认设置,系统频率为5 0 Hz。PSCAD软件中设置的采样频率为20 kHz。
系统稳定运行至0.5 s时,在距离A端50 km发生三相接地短路故障,故障持续时间0.1 s。测距端在A端。在线路中测得电流参数并经过相模变换得到β模电流,波形图如图2所示。
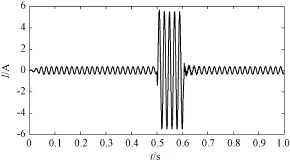
图2 β模电流仿真图
将β模电流利用SSI方法进行辨识,去SSI辨识阶数为10阶,辨识结果如表1所示。

表1 SSI分析结果
由表1知,幅值最大的频率为系统基频,除此之外,2 444.13 Hz频率为除基频外幅值最大的频率,即为输电线路中行波的固有频率。
通过PSCAD中的.out文件可以得到在此固有频率下的线路阻抗矩阵和导纳矩阵分别为
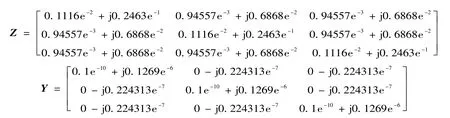
由式(24)和式(25)可求得模阻抗矩阵和模导纳矩阵分别为


则输电线路的模特征阻抗矩阵为

固有频率下的等效阻抗矩阵为

进而可由式(28)和式(29)求得测距端和故障端的反射系数矩阵。

进一步可求得测距端和故障端反射角矩阵分别为
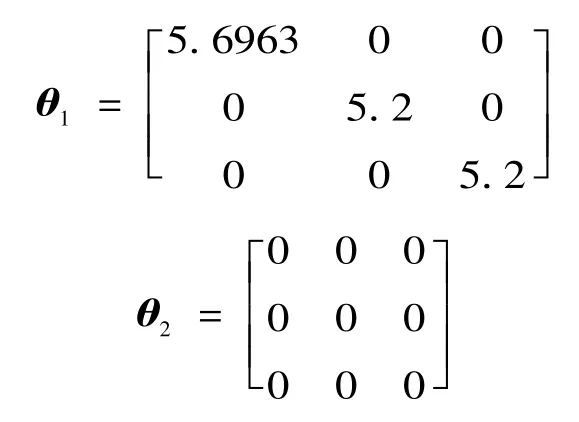
可由式(27)求得行波波速为
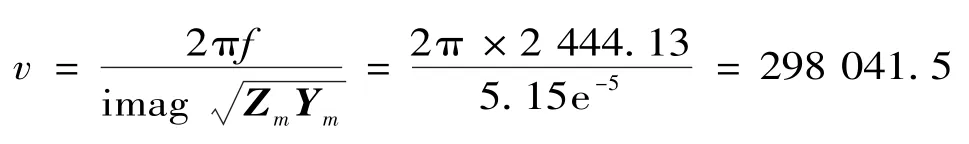
最后可由式(20)求得故障距离为

最后求得故障距离为50.4 km,误差只有0.97%,准确率较高,可有效辨识出故障距离。
3 结论
通过SSI算法可有效地辨识出故障线路中行波的固有频率,进而根据固有频率法可以准确判断出故障位置。在Matlab软件中编写SSI程序,在PSCAD中搭建两端系统模型,在输电线路中施加三相接地短路故障,通过SSI算法和固有频率法相结合可有效计算出故障位置。且采用SSI算法辨识时,系统阶数不需要取很多即可准确辨识出固有频率,具有很大的实际应用价值。
[1]AIEE Committee Report.Bibliography and summary of fault location methods[J].IEEE Transactions on the A-merican Institute of Electrical Engineers Power Apparatus and Systems,PartⅢ,1955,74(3):1423-1428.
[2]葛耀中.新型继电保护与故障测距原理与技术[M].西安:西安交通大学出版社,1996.
[3]陈双,林圣,李小鹏,等.基于系统阻抗自适应的行波固有频率测距方法[J].电网技术,2013,37(6):1739-1745.
[4]覃剑,陈祥训,郑健超.行波在输电线路上传播的色散研究[J].中国电机工程学报,1999,19(9):27 -30.
[5]李配配,黄家栋.配电网混合线路双端行波故障测距方法的研究[J].电力科学与工程,2011,27(11): 31-34.
[6]鹿洪刚,覃剑,陈祥训.35kV电力电缆在线故障测距仿真研究[J].电网技术,2008,32(24):81-87.
[7]邬林勇,何正友,钱清泉.单端行波故障测距的频域方法[J].中国电机工程学报,2008,28(25):99 -104.
[8]余亮,李志强.基于暂态信号频域分析的故障测距方法[J].电力建设,2013,34(5):96-98.
[9]林圣,武骁,何正友,等.基于行波固有频率的电网故障定位方法[J].电网技术,2013,37(1):270 -275.
[10]邬林勇.利用故障行波固有频率的单端行波故障测距法[D].成都:西南交通大学,2009.
[11]曹健,林涛,张蔓,等.电力系统间谐波检测方法[J].高电压技术,2008,34(8):1745-1750.
[12]庞浩,李东霞,俎云霄,等.应用FFT进行电力系统谐波分析的改进算法[J].中国电机工程学报,2003,23(6):50-54.
[13]Musha T,Kumazama T.Instantaneous structural intensity by the harmonic wavelet transform[J].Journal of Sound and Vibration,2007,306(1-2):377-388.
[14]徐俊明,魏文伟,夏沛.基于Prony算法的固有频率法输电线路故障定位[J].电测与仪表,2011,48(10):19-24.
[15]刘洋,田石柱.基于随机子空间的结构参数识别及振动台试验验证[J].地震工程与工程振动,2004,24(2):111-117.
[16]徐良,江见鲸,过静珺.随机子空间识别在悬索桥实验模态分析中的应用[J].工程力学,2002,19(4):46-49.
[17]周泽存,沈其工,方瑜,等.高电压技术[M].北京:中国电力出版社,2007.
Fault Location of Transmission Lines Based on Stochastic Subspace Identification Method and Travelling Wave Natural Frequency
Zhang Kai
(Weifang Power Supply Company,Shandong Electric Power Corporation,Weifang 261061,China)
The question of how to judge fault distance accurately and rapidly has great significance in the actual production run when a short circuit fault of transmission lines happens.When faults happen they produce transient state travelling waves.The frequency spectra of travelling waves are a fundamental characteristic frequency.This paper research on fault location is based on stochastic subspace identification and the natural frequency of traveling waves.Firstly,we use module current component based on phase-mode transformation,secondly we identify the natural frequency of traveling waves based on stochastic subspace identification.Then we calculate the wave velocity and module impedance admittance matrix at the natural frequency.Finally,we arrive at the distance to fault. Building the two-terminal system using PSCAD program,the simulation’s result show the way to find fault location with high accuracy.
fault location;stochastic subspace identification;natural frequency;traveling wave
TM773
A DOI:10.3969/j.issn.1672-0792.2015.05.010
2015-01-29。
张凯(1977-),男,工程师,主要从事输电线路运行检修及带电作业方面工作,E-mail:zk_0536@163.com。
