区间三角模糊多态贝叶斯网络可靠性分析方法研究

张瑞军　张路路　王晓伟　王囡囡

1.山东建筑大学,济南,2501012.山东省高校机械工程创新技术重点实验室,济南,250101

区间三角模糊多态贝叶斯网络可靠性分析方法研究

张瑞军1,2张路路1王晓伟1,2王囡囡1

1.山东建筑大学,济南,2501012.山东省高校机械工程创新技术重点实验室,济南,250101

针对传统系统可靠性分析方法在处理模糊信息方面的不足，建立了基于区间三角模糊贝叶斯网络的多态系统可靠性分析方法。通过区间三角模糊子集来描述根节点故障率;基于区间三角模糊子集,构建了区间三角模糊多态贝叶斯网络模型；研究了区间三角模糊多态贝叶斯网络可靠性分析算法，给出了求解叶节点故障模糊可能性与去模糊根节点后验概率的计算方法。最后,对塔机倾覆事故进行了可靠性分析,验证了该方法的有效性。

区间三角模糊;贝叶斯网络;多态系统;塔机倾覆事故

0　引言

可靠性表示产品或部件在规定时间和条件下完成规定任务的能力[1-2]。系统可靠性理论是可靠性理论的一条重要分支,包含事件树/故障树(event treee/fault tree,ET/FT)[3]、二元决策图(binary decision diagram,BDD)[4]、可靠性框图(reliability block diagram,RBD)[5]和贝叶斯网络(Bayesian network,BN)[6]等分析方法。在反向推理、处理模糊信息和建模等方面，BN都具有明显的优势，并已成功应用于可靠性分析、故障诊断和方案决策等领域[7-8]。文献[9-10]将BN带入到系统可靠性分析中,建立了基于BN的系统可靠性分析模型。该模型不但能实现系统可靠性的双向推理,而且能有效处理部件间的不确定故障逻辑关系，有效弥补其他可靠性分析方法在这些方面的不足。

上述基于BN的可靠性分析方法都是在假设节点故障率为精确值的基础上进行分析计算的，而实际工程中，历史数据的缺失以及多样的工作环境使得故障率具有模糊性，用精确值来描述往往不符合实际。文献[11-12]将模糊集合理论引入到BN中，用模糊子集代替精确值描述节点故障率，并应用于实例分析中。这些方法在一定程度上使BN具有处理模糊信息的能力，然而确定部件故障率模糊子集的上下限是很困难的，简单用定值表示往往造成信息丢失。

本文以模糊BN分析方法为基础，将区间变量引入到BN根节点构造中，建立区间三角模糊根节点,在此基础上构建了区间三角模糊BN可靠性分析模型，并将得到的这种新方法应用到塔式起重机倾覆事故分析中，对造成事故主要原因的重要度进行排序。

1　模糊BN简述

BN由一个有向无环图(directed acyclic graph,DAG)和若干条件概率表(conditional probability table,CPT)组成[13],可以表示为B=((N,E),p)。其中,(N,E)为一个具有n个节点的DAG,p为所有节点的条件概率表的集合,用来表达各节点与其父节点的关联联系。

模糊BN是将BN的连续节点变量推广到模糊节点变量[14]。模糊BN中的模糊性与不确定性不等同于随机性。随机性用来反映客观现实中的不确定性，而这里的模糊性是用来反映由于已知信息有限或其他原因造成的主观理解上的不确定性。

假设用Xi表示模糊BN的所有有限个节点,第i个节点可以用xi(i=1,2,…,n)表示,节点xi的所有m个模糊故障状态可表示为xi,j=(xi(1)，xi(2)，…,xi(m),用μi j(0≤μi j≤1；j=1，2，…，ri)来描述节点xi在模糊故障状态j时的隶属程度,隶属度表示节点故障信息的模糊程度,所有故障状态隶属度之和为1,即

(1)

式中,ri为故障状态个数。

2　区间三角模糊多态BN建模

2.1三角模糊BN节点的构建

针对传统BN中节点故障率用精确值来描述的不足,采用模糊子集表示的故障模糊可能性代替精确值来描述节点故障率。模糊子集的隶属函数有多种形式,常用的隶属函数有三角隶属函数、梯形隶属函数和正态隶属函数等。其中，三角隶属函数代数运算简单，常用于描述历史数据较少条件下的失效率。现实中针对塔机倾覆事故原因的统计数据较少,因此文中采用三角隶属函数来表述节点的故障率[12]。

假设节点xi在故障状态xi(ki)时的模糊可能性用P(xi(ki))表示,它为模糊子集{gl,gm,gu}。gm为模糊子集的中心,gm-gl和gu-gm分别为左右模糊区,随着模糊区的增大,模糊程度也越来越强。P(xi(ki))的隶属函数为

(2)

式中,g为故障概率。

式(2)用来表征节点故障率的模糊性,它的图形表现形式见图1。

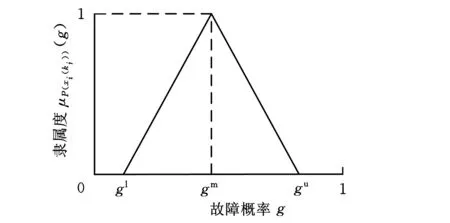
图1　P(xi(ki))的三角隶属函数

2.2区间三角模糊BN节点构建

现实中很难确定节点故障三角模糊子集的上限和下限,故引入区间变量代替精确值来表示三角模糊子集的上限和下限。节点xi在故障状态xi(ki)时的模糊可能性为

(3)

P′(xi(ki))的隶属函数为

μP′(xi(ki))(g)=

(4)

其曲线如图2所示。

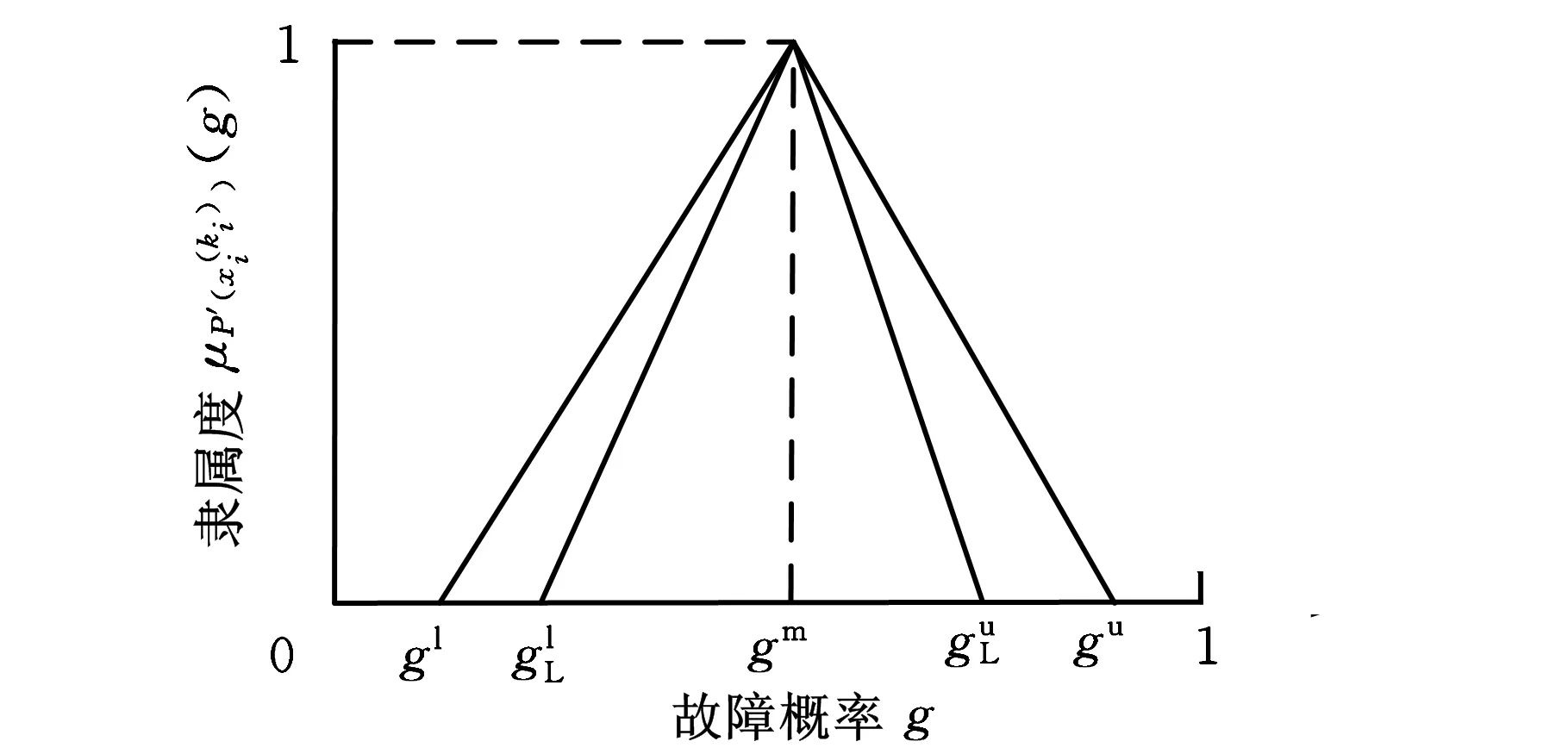
图2　P′(xi(ki))的区间三角隶属函数

2.3区间模糊多态BN的DAG

DAG为有向无环图,用来表示BN中的因果关系。在DAG中，有向边由父节点指向子节点。在BN中，根据父节点的先验概率以及父节点间的条件依赖关系，很容易求得任意父节点的后验概率。DAG结构的好坏影响着BN的系统分析能力,因而DAG的构造成为其在故障诊断应用中的一个“瓶颈”。区间模糊多态BN的DAG与传统BN的DAG在结构上是完全一样的，可由故障树转化得到。区间模糊BN的DAG结构与故障树图结构是一一对应的，往往由一个叶节点和多个根节点组成。

2.4区间模糊多态BN的CPT

传统BN的条件概率表假设部件和系统有两种故障状态——故障或安全。现实系统中,故障并非总是表现为“非此即彼”的二态性,而是表现出“亦此亦彼”的多态性。此外,传统BN的CPT是由FT直接映射而来的,描述部件间确定的故障逻辑关系。实际中，由于信息的模糊性，很难确定系统中部件间的故障逻辑关系，因此，用确定的故障逻辑关系描述部件间的逻辑关系必然影响分析结果的准确性。区间模糊贝叶斯网络CPT的构造结合了专家知识和实际经验，体现出了部件故障的多态性和部件间故障逻辑关系的模糊性，表1为图3所对应的区间模糊BN的CPT。

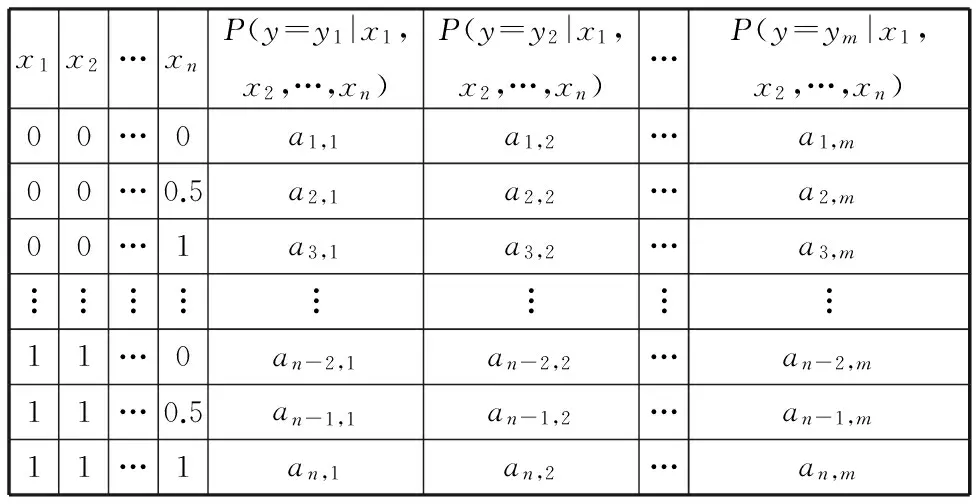
表1　区间模糊多态BN的CPT

表1中,m为叶节点的故障状态的个数,n为根节点的个数,P(y=yi|x1=x2=…=xn=0)描述所有根节点故障状态都为0(安全)的条件下,叶节点y故障状态为yi的条件概率。

3　基于区间三角模糊BN的可靠性分析方法

将系统中的n个基本事件用BN根节点表达,记为xi(i=1,2,…,n);系统分析中的顶事件转换成BN中的叶节点,记为T;系统中的其他m个事件转化为BN中的中间节点,记为yj(j=1,2,…,m);对于模糊BN的各节点，分别用模糊数xi(ki)、yj(kj)、Tv(ki=1，2,…,li;kj=1,2,…,lj;v=1,2,…,l)描述各相应根节点、中间节点、叶节点故障状态,xi(ki)表示根节点xi的故障状态;yj(kj)表示中间节点的故障状态;Tv表示叶节点的故障状态;v描述当前所处状态;l为状态总数。

3.1叶节点各故障状态模糊可能性

3.1.1叶节点各故障状态模糊可能性

若已知所有根节点的各故障状态的区间模糊可能性可以表示为P′(xi,ki),叶节点T处于故障状态Tv的区间模糊可能性记为

P′(T=Tv)=

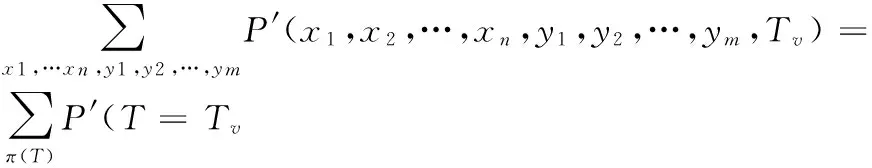
(5)

式中,π(T)是叶节点T的所有父节点集合;π(y1)为中间节点y1的所有父节点x1、x2、…、xn的集合。

3.1.2算法验证

以文献[12]中某载重车液压悬挂系统模糊贝叶斯网络为例,将文献中根节点各故障模糊可能性区间模糊化，并用区间模糊子集表示。例如，根节点x1故障状态为1的模糊可能性为{11.5,13.5,15.5},则利用区间模糊子集表示为[(11.5,11.5);13.5;(15.5,15.5)]。

利用式(5)可以求出叶节点T在其故障状态为1时的区间模糊可能性:

P′(T=1)=

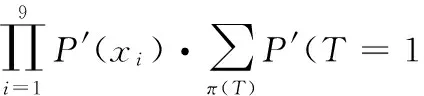
[(2.498,2.498);3.100;(3.702,3.702)](10-5h)

由结果可知,叶节点区间三角模糊子集的上下限变量区间的下边界与上边界重合，所得结果与文献[12]中利用三角模糊子集描述根节点故障模糊可能性所求结果相同，验证了式(5)的可行性。文献[12]中的根节点故障率的三角模糊子集上下边界为精确值，是区间的一种特殊形式，所以与文献[12]所提出的方法相比，本文提出的方法更具有一般性。

3.2去模糊根节点后验概率

3.2.1去模糊根节点后验概率

后验概率反映叶节点发生故障后根节点修正的故障概率，根据后验概率计算结果可以对系统可靠性状况作进一步了解。利用贝叶斯网络反向推理能力和去模糊计算方法得到的叶节点区间模糊可能性，可以推理得到任意根节点的后验概率。

叶节点T在故障状态Tv条件下,根节点xi在故障状态为xi(ki)时的后验概率为

(6)

3.2.2算法验证

以文献[15]中巷道运输车液压系统贝叶斯网络为例，对文献中的模糊根节点进行区间模糊化处理，用区间三角模糊子集描述根节点。

利用式(6)求得叶节点T故障状态为1的条件下,根节点x1去模糊后验概率：

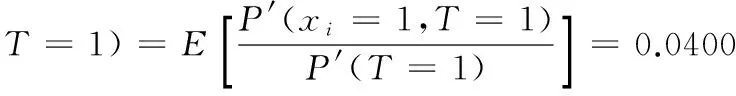
P″(xi=1|T=0.5)=0.0332

同理,可求出其他节点的后验概率,限于篇幅不再赘述。对比计算结果可知,本文所提后验概率计算方法所得结果与文献[15]所得计算结果相同，验证了式(6)的正确性与可行性。当能够获取根节点三角模糊子集上下变量的精确值时，选用文献[15]的方法，计算更加简单；当难以获取根节点三角模糊子集上下变量的精确值时，本文所提方法更加符合实际。

4　实例分析

塔机现场工作环境复杂,且事故后果往往较为严重,因此,塔机应具有较高的可靠性。为此,下面以避免塔机倾覆为目标,对塔机进行区间模糊可靠性评估。

塔机倾覆事故的主要原因可以分为以下三类：突然卸载、操作失误和超负荷工作。突然卸载主要包括起重断绳、吊物脱钩和起重折臂;操作失误主要包括故意违章操作、人为判断重量失误和人为判断操作失误；超负荷工作包括安全装置安装错位、斜吊力臂过大和轨道车连接螺栓松动。根据造成塔机倾覆事故原因之间的故障逻辑关系，以塔机倾覆事故为顶事件,建立图3所示的故障树。

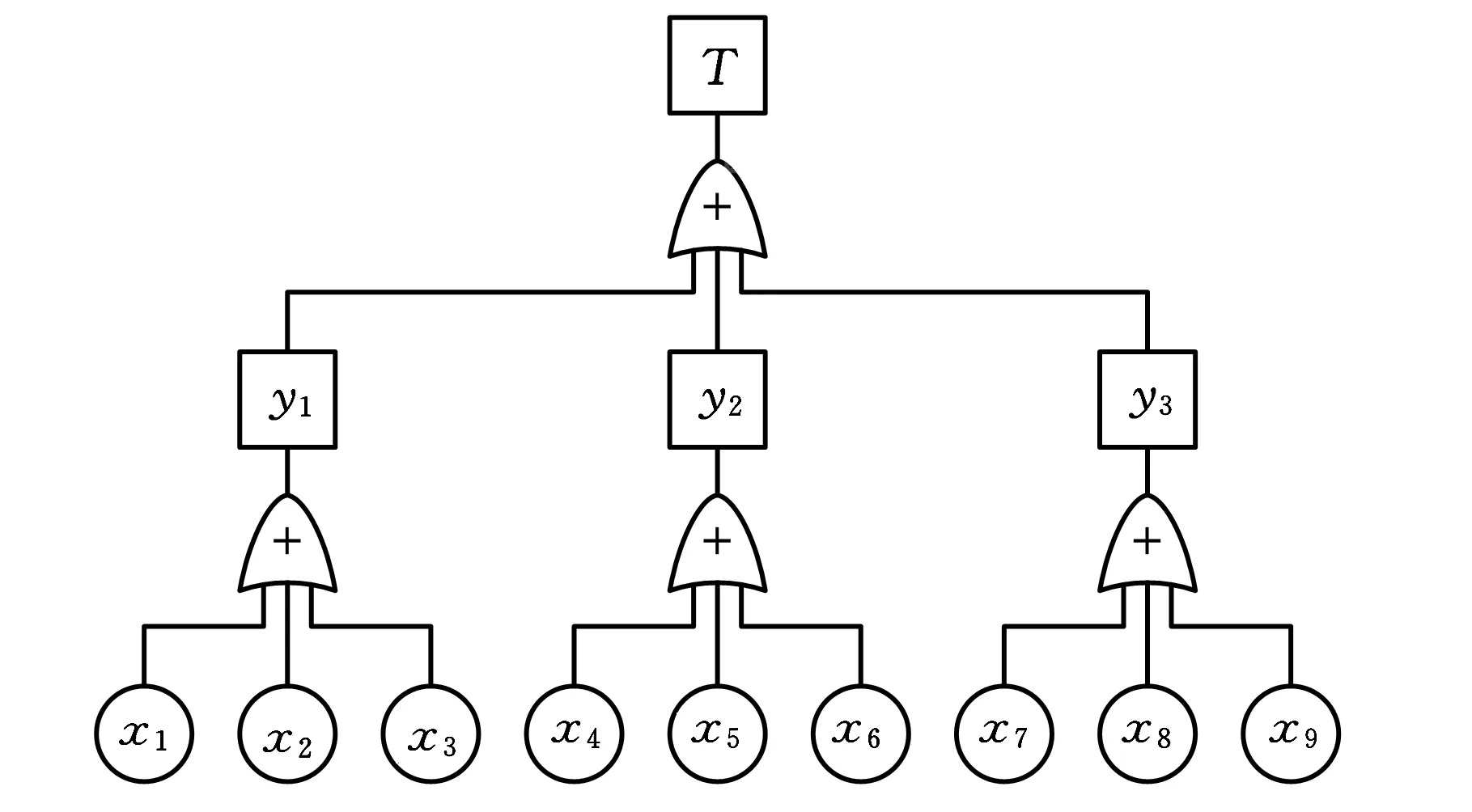
图3　塔机倾覆事故故障树

图3中,顶事件T代表塔机倾覆事故,x1～x9为底事件,分别代表突然卸载、操作失误、超负荷工作、起重断绳、吊物脱钩、起重折臂、安全装置失灵、斜吊力臂过大和人为判断重量失误;y1～y3为中间事件,分别代表突然卸载、操作失误和超负荷工作。根据由FT向BN转化方法[12],建立塔机倾覆事故的BN模型,如图4所示。

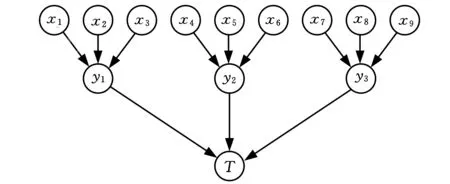
图4　塔机倾覆事故BN模型结构

假设,节点x1～x9、y1～y3和T的故障状态都为三态：无故障、半故障状态和完全故障，分别用模糊数0、0.5、1来表示。根据历史数据与专家经验获得根节点完全故障状态(用模糊数1来表示)下的区间模糊子集,如表2所示,根节点故障状态为0.5的区间模糊子集与故障状态为1的区间模糊子集相同。

表2根节点故障状态为1时的区间模糊子集

10-6h

考虑到现实情况中部件间故障逻辑关系的模糊不确定性,综合历史数据和专家经验得到各子节点的CPT,如表3所示。

表3　节点y1的CPT

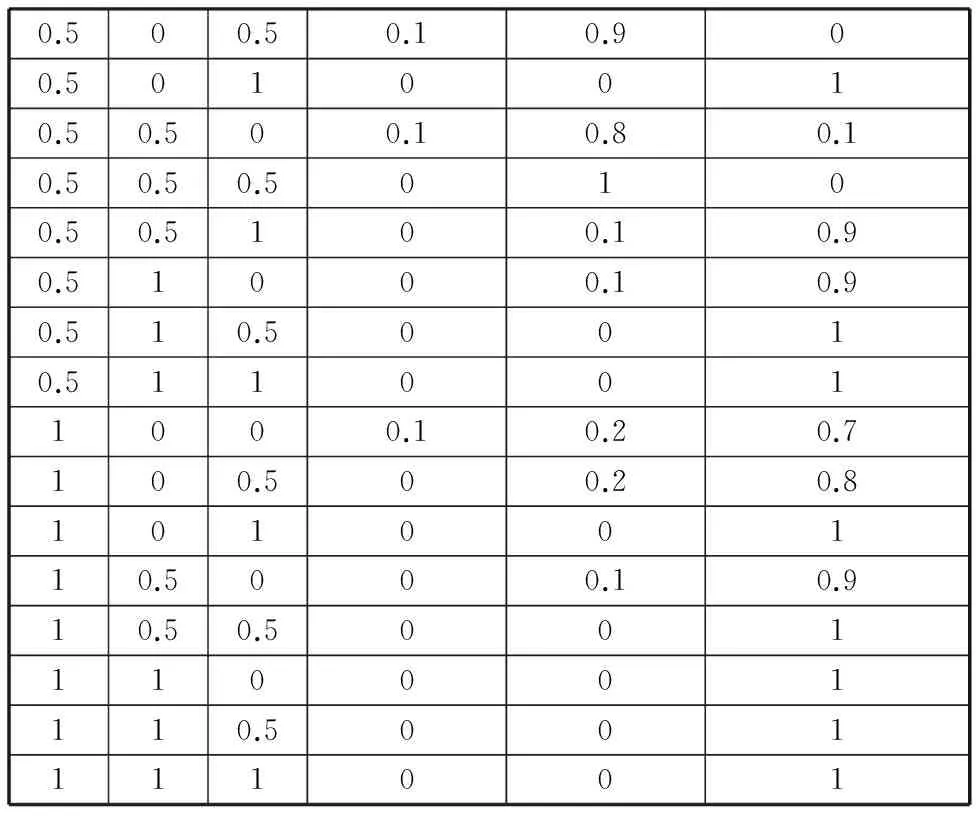
(续表3)

同理,可得到节点y2、y3、T的后验概率,限于篇幅,本文不再赘述。表3描述的是父节点处于不同故障组合状态条件下各子节点的条件概率。4.1叶节点各故障状态模糊子集

利用式(5)可以求出叶节点处于各故障状态时的模糊子集：

P′(T=1)=

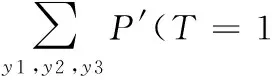
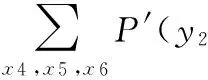
[(4.994,5.579);8.941;(12.188,12.773)](10-5/h)

P′(T=0.5)=[(3.560,3.969);6.511;

(8.864,9.373)](10-5/h)

4.2根节点后验概率

利用式(6),得到根节点x1的故障状态为1、叶节点T故障状态为1的去模糊后验概率：

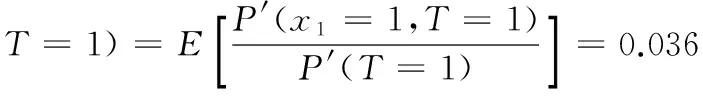
同理,可得到其他根节点的各故障状态在叶节点T故障发生条件下的后验概率,见表4。

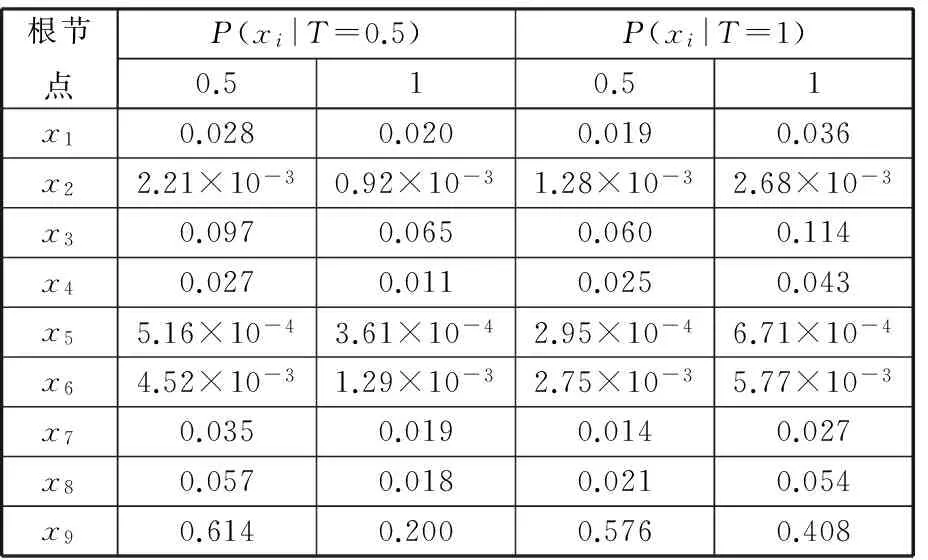
表4　根节点后验概率

在叶节点故障发生条件下得到的各根节点后验概率可用于系统故障诊断,应按照后验概率由大到小的顺序检测相应根节点。由表4可知,在系统处于半故障状态下,对半故障状态根节点进行检测应按照下列顺序进行：x9、x3、x8、x7、x1、x4、x6、x5,即首先检测的是人为判断重量失误,最后检测的应是吊物脱钩。

以上仅对节点故障率隶属函数为三角隶属函数的系统可靠性进行了讨论分析,实际系统中的节点故障率隶属函数还存在其他多种形式。对不同形式隶属函数同时存在的系统，隶属函数间的相互融合是系统可靠性建模的难点，如何对隶属函数进行离散化处理、拟合系统响应函数曲线将需进一步研究。

5　结论

(1)文中将区间变量引入到根节点构造中,建立了区间三角模糊子集描述节点的故障率，有效解决了现有系统可靠性分析方法在处理模糊故障率信息方面的不足。

(2)与传统贝叶斯网络只能处理确定故障机理的二态系统相比，该方法能够处理含不确定故障机理的多态系统。因此，传统贝叶斯网络可看作区间模糊贝叶斯网络的一个特例，区间模糊贝叶斯网络更具有一般性。

(3)将文中所提方法应用到塔机倾覆事故可靠性分析中，能够利用其正向推理能力，计算出叶节点各故障状态的区间三角模糊可能性，同时，还可以利用其反向推理能力，计算得到根节点的后验概率，为进一步进行系统故障诊断提供了依据，对于塔机可靠性设计具有一定的工程意义。

[1]王少萍.工程可靠性[M].北京:北京航空航天大学出版社,2000.

[2]Pate-Cornell E,Dillon R.Probabilistic Risk Analysis for the NASA Space Shuttle:a Brief History and Current Work[J].Reliability Engineering and System Safety,2001,74(3):345-352.

[3]姚成玉,赵静一.液压系统模糊故障树分析方法研究[J].中国机械工程,2007,18(14):1656-1675.

Yao Chengyu,Zhao Jingyi.Research on Fault Tree Analysis Method of Hydraulic System[J].China Mechanical Engineering,2007,18(14):1656-1675.

[4]杨莉琼,李世蓉,贾彬.基于二元决策图的建筑施工安全风险评估[J].系统工程理论与实践,2013,33(7):1889-1897.

Yang Liqiong,Li Shirong,Ji Bin.Safety Risk Assessment for Construction Project with BDD-based Method[J].Systems Engineering-Theory & Practice,2013,33(7):1889-1897.

[5]陈志诚,齐欢,魏军,等.基于可靠性框图的可靠性建模研究[J].工程设计学报,2011,18(6):407-411.

Chen Zhicheng,Qi Huan,Wei Jun,et al.Research on Reliability Modeling Based on Reliability Block Diagram[J].Journal of Engineering Design,2011,18(6):407-411.

[6]张路路,张瑞军,王晓伟,等.模糊支撑半径变量贝叶斯网络多态系统故障概率分析[J].工程设计学报,2014,21(5):405-411.

Zhang Lulu,Zhang Ruijun,Wang Xiaowei,et al.Failure Probability Analysis of Multi-state System Based on Bayesian Network with Fuzzy Support Radius Variable[J].Chinese Journal of Engineering Design,2014,21(5):405-411.

[7]刘希亮,陈桂明,李方溪,等.基于多传感器信息融合的贝叶斯网络故障诊断方法研究及应用[J].机械科学与技术,2013,32(1):91-95.

Liu Xiliang,Chen Guiming,Li Fangxi,et al. Fault Diagnosis Approach of Bayesian Networks Based on Multi-sensor Information Fusion and Application[J].Mechanical Science and Technology for Aerospace Engineering,2013,32(1):91-95.

[8]Zhu J,Deshmukh A.Application of Bayesian Decision Networks to Life Cycle Engineering in Green Design and Manufacturing[J].Engineering Applications of Artificial Intelligence,2003，16：91-103.

[9]张根保,刘佳,葛红玉.装配可靠性的动态贝叶斯网络建模与分析[J].中国机械工程,2012,23(2):211-215.Zhang Genbao,Liu Jia,Ge Hongyu.Modeling and Analysis for Assemble Reliability Based on Dynamic Bayesian Networks[J].China Mechanical Engineering,2012,23(2):211-215.

[10]Alyson G W,Aparna V H.Bayesian Networks for Multilevel System Reliability[J].Reliability Engineering and System Safety,2007,92(10):1413-1420.[11]陆莹,李启明,周志鹏.基于模糊贝叶斯网络的地铁运营安全风险预测[J].东南大学学报(自然科学版)，2010,40(5):1110-1114.

Lu Ying,Lu Qiming,Zhou Zhipeng.Safety Risk Prediction of Subway Operation Based on Fuzzy Bayesian Network[J].Journal of Southeast University(Natural Science Edition),2010,40(5):1110-1114.

[12]陈东宁,姚成玉.基于模糊贝叶斯网络的多态系统可靠性分析及在液压系统中的应用[J].机械工程学报,2012,48(16):166-183.

Chen Dongning,Yao Chengyu.Reliability Analysis of Multi-state System Based on Fuzzy Bayesian Networks and Application in Hydraulic System[J].Journal of Mechanical Engineering,2012,48(16):166-183.

[13]Jensen F V.An Introduction to Bayesian Networks[M].New York:Springer Press,1996.

[14]Pan Heping,Okello N,Mcmichael D,et al.Fuzzy Causal Probabilistic Networks and Multi-sensor Data Fusion[C]//SPIE International Symposium on Multispectral Image Processing.Wuhan,China,1998:550-561.

[15]姚成玉,陈东宁,王斌.基于T-S故障树和贝叶斯网络的模糊可靠性评估方法[J].机械工程学报,2013,49(6):89-97.

Yao Chengyu,Chen Dongning,Wang Bin.Fuzzy Reliability Assessment Method Based on T-S Fault Tree and Bayesian Network[J].Journal of Mechanical Engineering,2013,49(6):89-97.

(编辑张洋)

Research on Reliability of Multi-state System Based on Interval Triangular Fuzzy Bayesian Networks

Zhang Ruijun1,2Zhang Lulu1Wang Xiaowei1，2Wang Nannan1

1.Shandong Jianzhu University,Jinan,250101 2.Key Laboratory of Mechanical Engineering & Innovation Technology,Jinan,250101

In order to overcome the shortages of dealing with fuzzy information in traditional system reliability analysis methods,this paper proposed a new method of reliability analysis method based on interval triangular fuzzy multi-state Bayesian network.An interval triangular fuzzy subset was built to describe fault rate of root nodes.A model of the interval triangular fuzzy multi-states Bayesian networks was built based on the interval triangular fuzzy subset.The calculation methods of leaf node fault probability were proposed,and the deblured posterior probability was researched by the reliability analysis algorithms of interval triangular fuzzy multi-state Bayesian network.At last,the method was applied in the reliability analysis of tower crane overturning accident,which shows that the proposed method is feasibility.

interval triangular fuzzy;Bayesian network;multi-state system;tower crane overturning accident

2014-06-05

国家自然科学基金资助项目(51175312);山东建筑大学博士基金资助项目(XNBS1244)

TH122DOI:10.3969/j.issn.1004-132X.2015.08.018

张瑞军,男,1965年生。山东建筑大学机电工程学院教授。主要研究方向为建筑机械安全评估技术和结构系统可靠性设计理论。发表论文30余篇。张路路,男,1988年生。山东建筑大学机电工程学院硕士研究生。王晓伟,男,1971年生。山东建筑大学机电工程学院教授。王囡囡,女,1983年生。山东建筑大学机电工程学院讲师。